2018年中考中与生活相关的试题赏析

江苏省徐州市第二十六中学(221000) 史志伟

在2018年中考中,出现了与生活密切相关的新试题,即显示数学源于生活,同时数学又可以解决生活中的实际问题,现选取部分试题进行赏析.

例1(绍兴)利用如图1 的二维码可以进行身份识别.某校建立了一个身份识别系统, 图2 是某个学生的识别图案, 黑色小正方形表示1, 白色小正方形表示0.将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号, 其序号为a × 23+ b × 22+ c × 21+ d × 20.如图2 第一行数字从左到右依次为0, 1, 0, 1, 序号为0×23+1×22+0×21+1×20= 5, 表示该生为5 班学生.则表示6 班学生的识别图案是( )

图1

图2

分析根据班级序号的计算方法一一进行计算即可.

解对于B 选项,第一行数字从左到右依次为0,1,1,0,序号为0×23+1×22+1×21+0×20=6,表示该生为6班学生,故本题选B.

赏析本题出现了二维码这一近几年新生事物,学生对此很熟悉,微信的应用走进了大家的生活,一个微信号可产生二维码,但二维码对我们来说是抽象的;那么从生活中的数学角度,又如何识别学生的身份呢? 当然通过算式计算就可以求出学生所在的班级;从题型上看属于数学中的新定义题型,与生活息息相关,考查了学生的抽象辨析能力.

例2(温州)小明发现相机快门打开过程中,光圈大小变化如图3 所示,于是他绘制了如图4 所示的图形.图4 中六个形状大小都相同的四边形围成一个圆的内接六边形和一个小正六边形,若PQ 所在的直线经过点M,PB =5cm,小正六边形的面积为则该圆的半径为____cm.

图3

图4

分析随着人们生活水平的提高,很多家庭都拥有了相机,光圈的大小是受圆和多边形影响的,要设法寻找圆和两个正六边形之间的关系.

解设两个正六边形的中心为O,连接OP,OB,过点O 作OG ⊥PM于点G,OH ⊥AB 于点H,如图5 所示, 由题意得∠MNP = ∠NMP =∠MPN = 60°,所以△PMN 是一个等边三角形, 边长而且面积等于小正六边形的面积的故△PMN 的面积为因为OG ⊥PM,且O 是正六边形的中心,所以所以在R t △OPG 中,根据勾股定理得OP2=OG2+PG2,即OP2, 所以OP = 7, 设OB 为x, 因为OH ⊥A B 且O 是正六边形的中心, 所以所以在R t △PHO 中, 根据勾股定理得OP2= PH2+OH2,即解得：x1=8,x2=-3(舍),故该圆的半径为8cm,答案为8.

赏析没想到吧,相机中也有数学问题;在光圈变化过程中,通过正六边形、正三角形、圆的变换,构成了一幅美妙的数学画卷.解题中两次运用勾股定理,再加上三角函数,巧妙解决了问题;培养了学生的逻辑推理与几何直观能力.

例3(衢州)某游乐园有一个直径为16 米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3 米处达到最高,高度为5 米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图6 所示,以水平方向为x 轴,喷水池中心为原点建立直角坐标系.

图5

(1) 求水柱所在抛物线(第一象限部分)的函数表达式;

(2) 王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8 米的王师傅站立时必须在离水池中心多少米以内?

(3) 经检修评估,游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下,把水池的直径扩大到32 米, 各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

图6

分析(1) 根据顶点坐标可设二次函数的顶点式,代入点(8,0),求出a 的值,此题得解;

解(1) 设水柱所在抛物线(第一象限部分)的函数表达式为y =a(x-3)2+5(a0),将(8,0)代入得25a+5=0,解得所以水柱所在抛物线(第一象限部分)的函数表达式为

分析(2) 利用二次函数图像上点的坐标特征,求出当y =1.8 时x 的值,由此即可得出结论;

解(2) 当y = 1.8 时,有解得x1= -1(舍去),x2= 7,所以为了不被淋湿,身高1.8 米的王师傅站立时必须在离水池中心7 米以内.

分析(3) 利用二次函数图像上点的坐标特征可求出抛物线与y 轴的交点坐标, 由抛物线的形状不变可设改造后水柱所在抛物线(第一象限部分) 的函数表达式为代入点(16,0)可求出b 值,再利用配方法将二次函数表达式变形为顶点式,即可得出结论.

解(3) 当x = 0 时,设改造后水柱所在抛物线(第一象限部分) 的函数表达式为因为该函数图象过点(16,0),所以解得b = 3, 所以改造后水柱所在抛物线(第一象限部分) 的函数表达式为所以扩建改造后喷水池水柱的最大高度为米.

赏析利用数学建模思想,先解决抛物线问题,再根据实际需要引出安全问题及改扩建问题,彰显了数学为生活服务的宗旨.

例4(临安)用一条宽相等的足够长的纸条,打一个结,如图7 所示,然后轻轻拉紧、压平就可以得到如图8 所示的正五边形ABCDE,其中∠BAC =______度.

图7

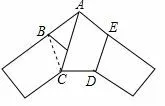
图8

分析利用多边形的内角和定理和等腰三角形的性质即可解决问题.

解因为五边形ABCDE 是正五边形,所以∠ABC =而△ABC 是等腰三角形, 所以∠BAC =∠BCA=36°,故答案为36.

赏析本题是折叠问题,通过折叠产生新图形正五边形,显出了一种美感;体现了积累基本活动经验这一核心素养.

例5(金华) 小靓用七巧板(如图9) 拼成一幅装饰图,如图10 所示,放入长方形ABCD 内,装饰图中的三角形顶点E,F 分别在边AB,BC 上,三角形 ①的边GD 在边AD上,则的值是____.

图9

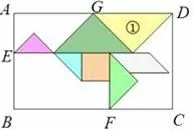
图10

分析可设原来七巧板的边长为4(或一个字母),在图10 中,需要作辅助线,寻求七巧板中相关图形线段之间的关系是关键,进而求出AB 与BC 的长.

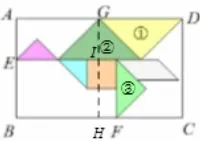
图11

解如图11,过G 作于H,交三角形 ②斜边于点I,则AB = GH = GI +HI,BC =AD = AG+GD = EI +GD,设原来七巧板的边长为4,则三角形 ②斜边的长度为4,三角形 ③斜边长则AB = GI +IH =而AG = EI = 4,GD = 4, 则BC = 8, 所以故答案为

赏析小小七巧板,构筑数学大舞台,七巧板中的相关图形的线段之间有密切的关系,这也是本题的突破所在.

例6(台湾)如图12 的宣传单为菜克印刷公司设计与印刷卡片计价方式的说明, 妮娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15 元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费, 则她至少需印多少张卡片, 才可使得卡片全数售出后的利润超过成本的2 成? ( )

图12

A.112 B.121 C.134 D.143

分析设妮娜需印x 张卡片,根据利润=收入-成本,结合利润超过成本的2 成,即可得出关于x 的一元一次不等式,解之即可得出x 的取值范围,取其内最小的整数即可得出结论.

解设妮娜需印x 张卡片,根据题意得15x-1000-5x ＞0.2(1000+5x),解得因为x 为整数,所以x ≥134.

答：妮娜至少需印134 张卡片,才可使得卡片全数售出后的利润超过成本的2 成,故选C.

王府饭店门口，矗立着一个大大的气囊，上写着：瑞恩·杰克苏婷婷婚礼志喜。一辆挂彩的红色宝马驶来，立刻鞭炮齐鸣，鼓乐声起。车门打开，身着婚纱的苏婷婷和身着礼服的杰克下了车，周围人鼓起掌来。杰克拉着苏婷婷的手，向周围人群连连挥手。彩丝彩带同时在两人头上飘下。

赏析台湾的这个中考题考查的是利润问题,根据题目意思列出不等式即可,体现数学建模思想.

例7(达州)如图13,在物理课上,老师将挂在弹簧测力计下端的铁块浸没于水中,然后缓慢匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧测力计的读数y(单位：N)与铁块被提起的高度x(单位：cm)之间的函数关系的大致图像是( )

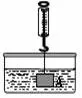
图13

分析根据题意,利用分类讨论的数学思想可以解答本题.

解由题意可知,铁块露出水面以前,F拉+F浮= G,浮力不变,故此过程中弹簧的度数不变;当铁块慢慢露出水面开始,浮力减小,则拉力增加;当铁块完全露出水面后,拉力等于重力,故选D.

赏析本题考查函数图像,解答本题的关键是明确题意,要运用物理学的知识,再运用数形结合和分类讨论的数学思想解答,展现了数学与其他学科的融合.

图14

练习2(随州)随州市新水一桥(如图15)设计灵感来源于市花--兰花,采用蝴蝶兰斜拉桥方案,设计长度为258 米, 宽32 米, 为双向六车道, 2018年4 月3 日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图16 所示, 索塔AB 和斜拉索(图中只画出最短的斜拉索DE 和最长的斜拉索AC) 均在同一水平面内,BC 在水平桥面上.已知∠ABC = ∠DEB = 45°,∠ACB =30°,BE =6 米,AB =5BD.

(1) 求最短的斜拉索DE 的长;

(2) 求最长的斜拉索AC 的长.

图15

图16

通过以上试题分析和练习,我们知道对于与生活相关的问题,这也是各地中考试题的热点;在以后的教学中,我们要关注这类吃穿住行的问题;在平时的课堂中,首先,说明生活中孕育着数学问题,另一方面,生活中的问题是可以用数学解决的;这样能充分激发学生学习数学的兴趣,兴趣是最好的老师,学生的数学综合能力自然能提高.其次,注重数学实验,在教学中,还要培养学生动手实践的能力,让学生亲自操作,比如拼图、旋转、平移、翻折折纸等,手脑并用,在实验中积累经验,思考中增长智慧.最后,注重数学与其他学科的融合;中考中,不仅考查数学知识,还有语文、物理、生物等知识,教师在平时多留心此类的问题,也可以买些数学科普读物让同学们去阅读,开阔视野,培养思维.通过以上三个方面,就会培养学生的创新意识与应用意识,培养用数学的眼光观察世界、用数学的语言表达世界、用数学的思维思考世界的能力,从而提高学生的核心素养.