用好教材题源,设计压轴题库

浙江省仙居县安洲中学(317300) 吴刚

教材习题是解题教学的基础训练题源,但如果没有好的设计提升,那也只是停留于基础训练,而不是解题的坚强后盾.学生解题困惑的表面是内容讲的不够多,题目练得不够深,其实际是教学中不注重核心素养的培养,背和记代替学生的体验和探究.如何用好教材题源,提升演变成压轴大题;如何把难题大题设计分解,回归教材基本题,结合自己的教学实际谈具体操作,以期抛砖引玉.

1 基本习题,变式压轴

案例1(人教版八年级上13.3 等腰三角形配套的单元习题)如图1,△ABC 与△DCE 是等边三角形,且B、C、E共线.BD 与AE,AC 分别相交于点P,M,CD 与AE 相交于点N.求证：BD =AE.

老师层层设计, 步步追问, 由浅入深, 让学生发现问题,解决问题.

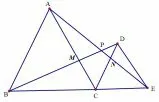
图1

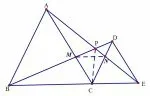
图2

问题1在不添加任何条件的前提下,能得到结论

(1) BD =AE,∠APB =60°;

(2) △MCD 与△NCE 全等;

(3) CM =CN,AN =BM,EN =DM;

问题2如图2,如果允许连接其他线段,还能提出

(4) △MCN 是等边三角形;

(5) MN 平行BE;

(6) 连接PC,可以证明PE 是∠BPE 的角平分线......

问题3如图3,B、C、E 不共线,△DCE 绕点C 顺时针旋转一定角度,上述结论哪些成立?

问题4如图4, 把两个等边三角形变成等腰直角三角形,上述结论哪些成立?

问题5如图5,在问题4 的基础上,B、C、E 不共线,上述结论哪些成立?

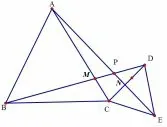
图3

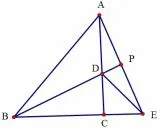
图4

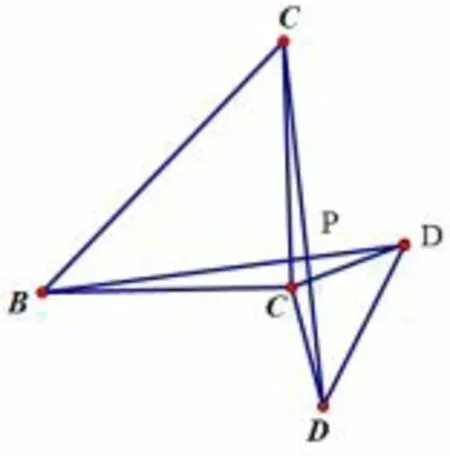
图5

归纳内化立足图形的旋转变换过程,研究一个图形的变与不变,让学生真正把握数学的本质,在变中找不变,以不变应万变.特殊到一般的解题思想和变式教学,培养学生的数学建模、直观想象、逻辑推理等数学核心素养.

2 压轴大题,化身基本

综合解题指导重点学习怎样感知问题、怎样分析思路、怎样选择合理的思想方法和知识解决问题,转化类比为熟悉的题目.通过训练,形成“套路”,找到解题的突破口.

案例2(2015 山东省德州市)如图6, ⊙O 的半径为1, A,P,B,C 是⊙O 上的四个点,∠APC =∠CPB =60°.

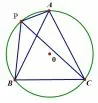
图6

(1) 判断△ABC 的形状：

(2) 试探究线段PA,PB,PC 之间的数量关系,并证明结论;

(3) 当点P 位于弧AB 的什么位置时, 四边形APBC的面积最大? 求出最大面积.

直接解题(2)、(3)两问提高太快,难度较大.课本有类似原题.

案例3人教版(2014)九年级上册P90 第13 题.

如图6, A,P,B,C 是⊙O 上的四个点, ∠APC =∠CPB =60°.判断△ABC 的形状,并证明你的结论.

这是一道基本题,如果就题论题,到此结束,那太可惜了.教师应该立足教材, 让学生探究, 提出问题, 进行变式教学.设计的时候注意题目的难易程度,应该由浅入深,层层逼近,有梯度,有深度,其最终目的让学生明白,所谓的难题大题其实是有章可循,类比转化为常规的思路、思想、方法.

变式1如图7,P 是弧AB 的上的点,当P 在何处时,四边形APBO是菱形.

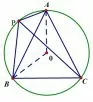
图7

分析注意画图,几何应该从直观入手,发现合适的位置、结论,再思考严密的证明,推理的依据.

变式2如图6,求证：PC = PA+PB(或者让学生探究三者的数量关系,再证明).

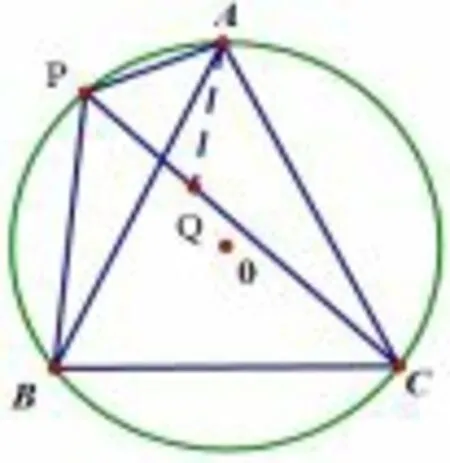
图8

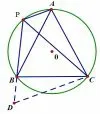
图9

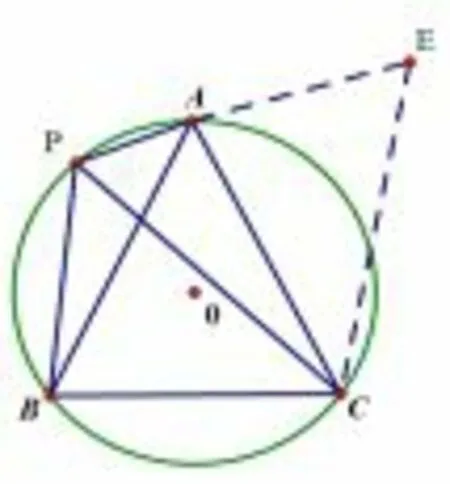
图10

分析可以要求学生测量三者的具体长度,发现结论,转化为常规的截长补短法,辅助线可以如图8 截长法,如图9、图10 补短法,要求学生分别尝试两种方法,一题多解,分别分析落实具体证明流程.也可以站在旋转的角度去添辅助线,将△PAC 绕点C 逆时针旋转60 度与△PBC 组成一个大三角形,证明是等边三角形,反之也可.体验两者的具体区别和共性,使得做一题练一串,做一题,解一片.

变式3如图6,在原题条件下,若再有PA=1,PB =2,求四边形APBC 的面积.

分析利用变式2,如图11,如图12,旋转等值转化为求△PDC 或△EPC 的面积.

变式4如图6,在原题条件下,点P 在何处时,四边形APBC 的面积最大.

分析可以直接用变式3 的结论,四边形APBC 的面积就是等边三角形的面积,四边形面积最大就是等边三角形的面积最大,就是等边三角形的边最大,当然是过圆心的直径时最大.如图13,也可以站在面积就是底和高的乘积,底边定值,PM +PN 的值最大,就是面积最大,此时为直径.

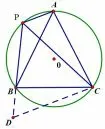
图11

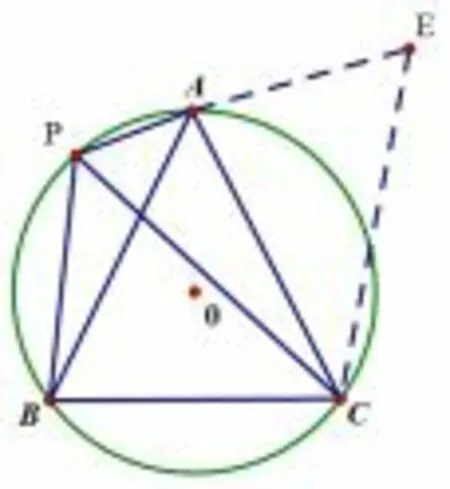
图12

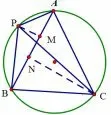
图13

以上各题的变式,其实际就是命题者从简单到难的设计题目.教师的变式教学,其实际就是启发学生如何解决大题、难题的思路,如何熟练转化.

如果直接考变式(3)(4),那该如何思考分析? 那不就是案列2：(2015 山东省德州市)的问题.我们采用波利亚解题表的解题策略四部曲：弄清题意、拟定方案、执行方案、总结回顾.重新整理一下解题的整个流程.

1.弄清题意

观察要求的问题,这是什么类型的问题? 见过类似的问题吗? 圆背景中的题目.周角定理入手,标条件,标条件推出的结论.自然得到△ABC 等边三角形的结论.对于(2)问,探究三边关系,转化的思想入手,平时一般怎么考虑? 首先直接测量,发现三条线段的结论PA+PB = PC,直观想象的核心素养; 或者转化一般到特殊的方法,当点P 在点A 时,PA=0,PB =AB,所以PA+PB =PC(点P 在B 点时同理);点P 在中点时,计算知道PA = PB = 0.5PC,所以PA+PB = PC.截长补短法.对于(3)问,面积问题最大,或面积的函数表达式,利用函数的性质求解,或直接割补法转化为规则图形的面积加减.

2.拟定方案

类比转化,转为熟悉类型,或者方法的套路,由(2)结论,PC = PA+PB,尝试截长或补短的两种可能途径,添加辅助线,构造三角形的全等,或者三边转化为两边相等,利用等角对等边的思路.四边形PBCA 的面积就是△PCE 的面积.对于第(3)个问题,如果有(2)做基础,那么就转化简单了,四边形PBCA 的面积就是△PCE 的面积,四边形面积最大就是三角形的面积最大,就是PC 最大即PC 为直径时.也可这样思考,△ABC 的边是固定不变的,面积最大就是高之和PM +PN 最大,即PC 是过圆心的直径时面积最大.

3.执行方案

选定一个可行的角度,具体解答,如图14 或如图15,从已知开始严密推理.

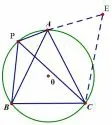
图14

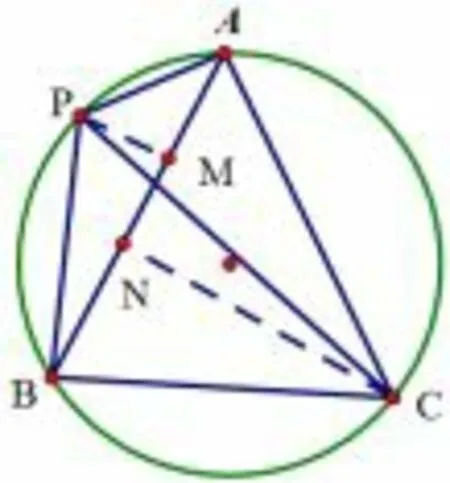
图15

4.回顾总结

解题中关键如何转化为熟悉类型方法,使得问题变得简单.如何一般到特殊,直观想象,数学建模,如何逻辑推理? 当题目有多个小问题的时候,你有什么解题经验吗? 解题者要注意这个信息：题目之间往往是上下关联,层层递进.上一题的结论经常是下一题的隐含条件或者为下一题提供思路.要用联系整体的眼光看各个小题,体会它们之间的关联,包括题目提供的图,主动利用题目的已知条件和题目顺序.通过一步步的自我提问将题目难点逐步突破,这也是分析问题,解决问题的有效方式.

3 感悟反思

数学教育家波利亚曾经提出：“学习任何知识的最佳途径是由自己发现,因为这种发现理解最深,也最容易掌握其中的内在规律、性质和联系.”[1]最有效的复习,是通过讲解一道题,建立基本模型,总结出一般思想和方法,串起一类题.培养学学生化归能力,“将未知的、陌生的和复杂的问题通过演绎归纳,转化为已知的、熟悉的和简单问题”.[2]