一类具比例时滞Hopfield神经网络的全局渐近稳定性
周 瑞, 周立群
(天津师范大学 数学科学学院, 天津 300387)
1982年,Hopfield 提出Hopfield神经网络(HNNs),并引入了能量函数。1984年,Hopfield证明了该模型能够实现的电子电路,这些取得的成果使得HNNs在模式识别、最优控制、联想记忆、图像处理等方面的应用具有非常优越的潜力[1-4],因此得到了学者们的广泛研究[5-11]。由于在神经网络模型中,时滞是不可避免的,所以具有时滞的HNNs同样也被广泛探讨。文献[5]构造密度函数和应用线性化方法,得到了HNNs几乎处处稳定的充分条件和必要条件。文献[6]提出了离散型HNNs等效矩阵的概念,获得了研究其收敛性的一种新方法。文献[7]通过Lyapunov函数方法,讨论脉冲时滞HNNs平衡点的存在唯一性和全局稳定性。文献[8]通过构造合适Lyapunov泛函,给出了HNNs平衡点稳定性的充分条件。文献[9]得到了HNNs平衡点唯一且全局渐近稳定的充分条件。文献[10]讨论了常时滞HNNs的全局渐近稳定性。
一个神经网络通常具有空间的特性,这是由于神经网络中有大量的各种尺寸轴突的平行路径存在。在某些情况下,根据网络的拓扑和材料,在神经网络中引用比例时滞是合理的。如果比例时滞因子已知,具比例时滞的HNNs的优点是可以根据网络允许的最大时滞来控制网络的运行时间。比例时滞是一种无界时变时滞,且比例时滞系统在计算机科学、电子学等领域发挥着重要的作用。2011年,在文献[11]中比例时滞首次被引入CNNs至今,得到了众多学者的广泛关注。目前对具比例时滞神经网络动力学行为的研究,已经取得了大量研究成果[11-22]。文献[11-17]通过构造合适的Lyapunov泛函,应用矩阵理论及不等式技巧等方法研究了几类具比例时滞递归神经网络的渐近稳定性、周期性等。文献[18]应用矩阵谱半径理论、构造Lyapunov泛函,研究具比例时滞细胞神经网络稳定性。文献[19]应用固定点定理,探讨了一类具比例时滞脉冲递归神经网络的全局稳定性。文献[20]应用 Lyapunov-Krasovskii函数,探讨了具有多比例延迟的神经网络的均方稳定性。文献[21-22]应用了微分不等式,探讨了细胞神经网络的稳定性。
综上所述,受到文献[11,13,18]研究方法的启发,本文研究一类具比例时滞HNNs的全局渐近稳定性,应用Barbalat引理,构造合适的Lyapunov泛函,结合Lipschitz条件,得了保证该系统全局渐近稳定的充分条件。
1 模型与预备知识
考虑如下模型:
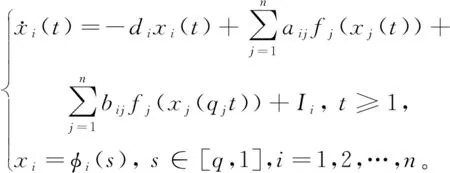
(1)

现在对fj作如下假设:
(A1)fj(j=1,2,…,n)在R上有界;
(A2)存在σj>0,j=1,2,…,n,使得
|fj(x)-fj(y)|<σj|x-y|,x,y∈R。
(2)
令
yi(t)=xi(et),
(3)
则系统(1)可等价变换成如下系统[23]
(4)


定义1称系统(1)的平衡点x*是全局渐近稳定的(GAS),若对于系统(1)的任何初始值φi(s),都满足
定义2称系统(4)的平衡点y*是GAS,若对于系统(4)的任何初始值ψi(s),都满足
引理1[24]若激励函数fj(j=1,2,…,n)满足(A1)和(A2),则方程(1)所有解在[0,+∞)上均有界。

2 平衡点的全局渐近稳定性
定理1若条件(A1)和(A2)成立,且
则系统(4)的平衡点y*是GAS。


(5)
取如下Lyapunov泛函
(6)
沿式(5)计算V的上右Dini导数D+V,由(A2),得
D+V(t)=
bijgj(zj(t-τj))]}sgnzj(t)+
(7)
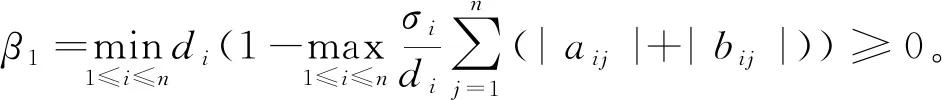
由上式,可知

即
即系统(4)的平衡点y*是GAS。
注1如果不将比例时滞HNNs转换成等价的常时滞HNNs,在比例时滞HNNs的稳定性的推导过程中,比例时滞函数的无界性很难被直接处理。且比例时滞是不同于无界的分布时滞,因为分布时滞的核函数具有较好性质,在推导过程中无界性容易被克服。
定理2若条件(A1)和(A2)成立,且
σi(|aji|+|bji|)),
则系统(4)的平衡点y*是GAS。
证明取如下Lyapunov泛函
(8)
沿式(5)的解计算V(t)的导数,可得
(9)
由2ab≤a2+b2与(A2),可得
(10)

由式(10),有
由上式,可知
余下部分同由定理1的证明类似,于是
从而可知系统(4)的平衡点y*是GAS。
注2若在式(1)中,qj=1,系统(1)和系统(5)就是无时滞的神经网络,本文所得结果适合该无时滞神经网络。
3 算 例
例1考虑如下二维神经网络
(11)

选择fi(xi)=0.5(|xi+1|-|xi-1|),Lipschitz常数为σi=1,i=1,2。计算得
(|a11|+|b11|)σ1+(|a12|+|b12|)σ1=4.1,
(|a21|+|b21|)σ2+(|a22|+|b22|)σ2=4.2,
于是,有
且
4.7=d1>4.2, 5.1=d2>4.2。
满足定理1,因此系统(11)是GAS的。
另一方面,计算得
|b12|)σ2+(|a11|+|b11|)σ1+
(|a21|+|b21|)σ1}=3.65,
|b22|)σ2+(|a12|+|b12|)σ2+
(|a22|+|b22|)σ2}=4.65,
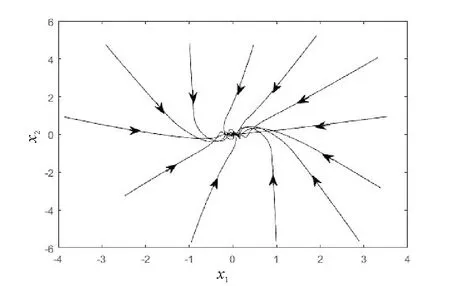
图1 系统(11)的相轨迹Fig.1 Phase trajectory of system (11)
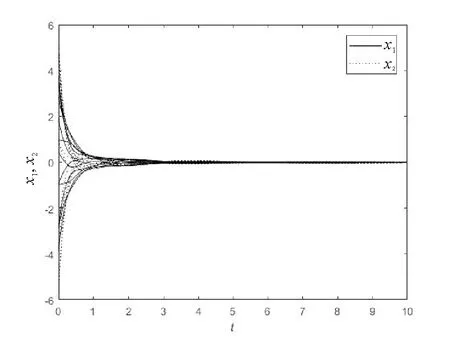
图2 系统(11)的时间响应曲线Fig.2 Response time curves of system (11)
因而,有
|bji|))=4.65,
并且
4.7=d1>4.65,5.1=d2>4.65。
满足定理2的条件, 因此系统(11)是GAS。系统(11)的平衡点为(0,0)T,利用Matlab软件画出系统(11)的相轨迹和时间响应曲线,见图1和2,由此可以直观地看出系统(11)是GAS。
例2考虑如下三维神经网络
(12)
其中


q1=0.4,q2=0.5,q3=0.8。
选择fi(xi)=0.5(|xi+1|-|xi-1|),则Lipschitz常数为σi=1,i=1,2,3。计算得
(|a11|+|b11|)σ1+(|a12|+|b12|)σ1+
(|a13|+|b13|)σ1=2.1+2+1.1=5.2,
(|a21|+|b21|)σ2+(|a22|+|b22|)σ2+
(|a23|+|b23|)σ2=2.1+2.1+2=6.2,
(|a31|+|b31|)σ3+(|a32|+|b32|)σ3+
(|a33|+|b33|)σ3=1+1.1+2.2=4.3,
于是,有
且
6.3=d1>6.2, 6.5=d2>6.2, 7=d3>6.2,
满足定理1,因此系统(12)是GAS。
另一方面,计算得
|b12|)σ2+(|a13|+|b13|)σ3+(|a11|+
|b11|)σ1+(|a21|+|b21|)σ1+(|a31|+
|b31|)σ1}=5.2,
|b22|)σ2+(|a23|+|b23|)σ3+(|a12|+
|b12|)σ2+(|a22|+|b22|)σ2+(|a32|+
|b32|)σ2}=5.7,
|b32|)σ2+(|a33|+|b33|)σ3+(|a13|+
|b13|)σ3+(|a23|+|b23|)σ3+(|a33|+
|b33|)σ3}=4.8,
于是
σi(|aji|+|bji|))=5.7,

图3 系统(12)的相轨迹Fig.3 Phase trajectory of system (12)
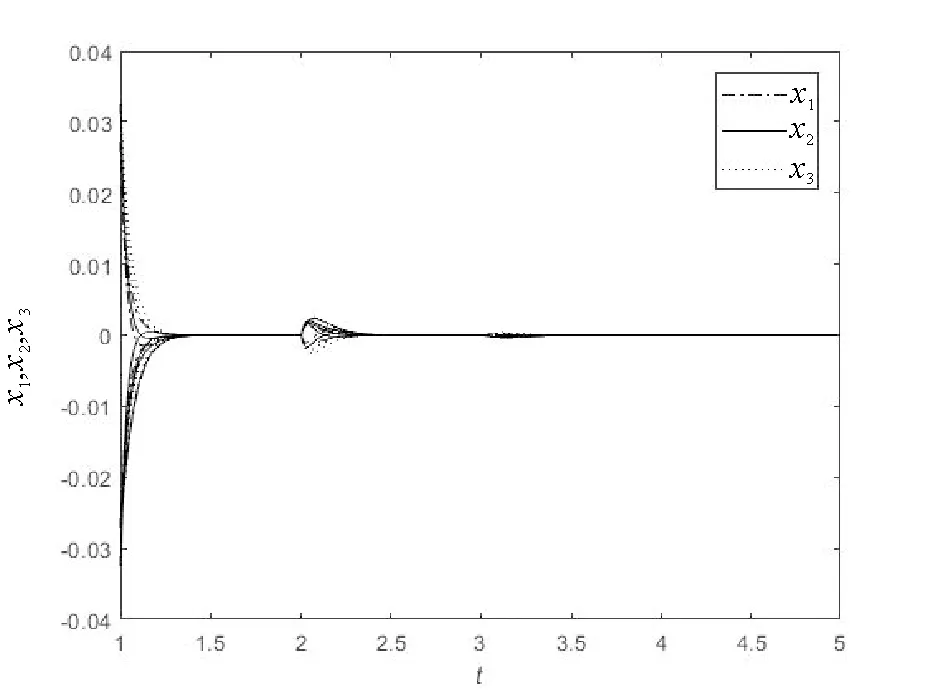
图4 系统(12)的时间响应曲线Fig.4 Response time curves of system (12)
且
6.3=d1>5.7, 6.5=d2>5.7, 7=d3>5.7。
满足定理2的条件,因此系统(12)是GAS。系统(12)的平衡点为(0,0,0)T,利用Matlab软件画出系统(12)的相轨迹及时间响应曲线,见图3和4,由此可以直观地看出系统(12)是GAS。
4 结 语
在激活函数满足有界且全局Lipschitz连续的前提下,应用Barbalat定理、常数变易法和构造Lyapunov泛函,研究了一类具比例时滞Hopfield神经网络的稳定性,得到了保证该系统全局渐近稳定性的两个充分条件,该条件简单,易于验证。其中非线性变换yi(t)=xi(et)将无界时滞系统等价变换成常时滞变系数系统,使问题由难变易,这种方法还可以用于其他神经网络的动力学行为的研究。进一步的研究工作,是将本文所得结果应用于二次规划问题的求解当中去。

