从《代数学》到《代数术》的几个相关问题研究
张必胜
(贵州师范大学 教育学院,贵州 贵阳 550025)
纵观数学发展史,中外在代数理论方面都有着杰出的成就。世界各国都有用文字来表示数字及其简单计算的历史,巴比伦从算术方法向代数运算的转变就是代数演化的结果。古希腊数学家丢番图(Diophantus,246—330)在其所著Arithmetica(《算术》)中讨论了不定方程求解问题。阿拉伯数学家阿尔·花拉子米(Al-Khwarizimi,780—850)撰写了经典著作al-kitapal-mukhtasarfihisapal-jabr(《还原和对消计算概要》),后来al-jabr演变为algebra。在这本著作中,详细讨论了方程的项及其运算,其核心是解方程。花拉子米的代数学在文艺复兴后得到了发展,特别是16~17世纪的法国数学家弗朗索瓦·韦达(Franciscus Vieta,1540—1603)和勒内·笛卡尔(René Descartes,1596—1650)关于用文字的表示数学及其运算的方法标志着符号代数进入了新的发展时期。后来,代数方程求解中出现了三次方程的解法。随后围绕四次方程,五次及五次以上代数方程根式可解性的研究诞生了新的代数学理论,从此以后的代数学从初等代数进入了抽象代数的范畴。
同样,我国代数学发展也经历了漫长的发展历史。我国代数学从早期的算术运算,到开方、多项式方程求解、高次方程求解、多元高次方程组求解等理论。传统代数学在宋元时期达到了顶峰,宋元时期的数学家关注不定分析、代数方程和级数求和问题等方面。在不定方程方面有演纪术和大衍术;在代数方程方面有天元术、开方术和四元术;在级数求和方面有垛积术和招差术等。在不定分析中出现的“中国剩余定理”即为一次同余式的求解问题,而数学家给出的大衍术是数学家的纯粹数学创造。天元术是建立代数方程,这是因为中国传统科学中历法的需要,而其中出现的增乘开方法则为多项式方程的数值解。垛积术和招差术中则出现了更为复杂的代数表达式和多项式运算。
1 引入简史
尽管“代数”与“代数学”两词汇在汉语中的出现晚至清末。然而,早在18世纪初期,西方代数学基本理论就已传入中国,当时被称为“借根方”。1711年,康熙皇帝爱新觉罗·玄烨(1654—1722)与赵宏燮(1656—1722)讨论代数学相关问题时就认为“算法之理,皆出于《易经》,即西洋算法亦善,原系中国算法,彼称为‘阿尔朱巴尔’,‘阿尔朱巴尔’者,传自东方之谓也。”随后,法国传教士傅圣泽(Jean Francoise Foucquet,1663—1740)为爱新觉罗·玄烨学习代数学而著《阿尔热巴拉新法》一书。然而,该著作并没有引起广泛关注,而被认为是难以理解之理论,更不被接受。西方代数理论正式引入中国最早是从英国汉学家伟烈亚力(Alexander Wylie,1815—1887)于1853年出版的《算学启蒙》开始的,在《数学启蒙》中,介绍了一些代数学的基本理论,内容涉及到了计数法、四则运算、乘方、开方和对数运算等。意图在循序渐进地向中国介绍西方代数学,并且首次给出了“代数”这一专业术语。伟烈亚力在《数学启蒙》的序言中给出了这样的叙述“余自西土远来中国,以传耶稣之道为本,余则兼习艺能。爱述一书,曰《数学启蒙),凡二卷,举以授塾中学徒,由浅及深,则其知之也易。……则有代数、微分诸书在,余将续梓之。俾览其全者,知中西二法,虽疏密详简之不同,要之名异而实同,术异而理同也。”[1]指出他除了介绍《数学启蒙》中的代数理论外,还将翻译出版《代数学》和《代微积拾级》等著作。《数学启蒙》中主要介绍的是加减乘除法则、约分、通分、开方、对数、对数运算和对数表使用等初等代数问题。在序言中伟烈亚力指出了此书的基础是康熙御制的《数理精蕴》,同时有的习题参考了利玛窦(Matteo Ricci,1522—1610)和李之藻(1565—1630)的《同文算指》和陈杰(不详)的《算法大成》。1859年,清末数学家李善兰(1811—1882)和汉学家伟烈亚力合作翻译英国数学家德摩根(Augustus De Morgan,1806—1871)的著作ElementofAlgebra,并且译名为《代数学》,其中讨论了代数学相关内容[2]。同年出版的《代微积拾级》中也出现了“代数”一词[3]。《代微积拾级》中第一个字“代”即为代数。1873年,清末数学家华蘅芳(1833—1902)和英国传教士傅兰雅(John Fryer,1839—1928)一起合作翻译了英国数学家华里司(William Wallace,1768—1843)的著作Algebra,译著名为《代数术》[4]。在其中,仍然采用“代数”一词,于是,“代数”一词被广泛运用并且沿用至今。
2 承前启后
对比《代数学》和《代数术》及其底本的主要内容,可以得出二译著是之间是承前启后之间的关系[5-6]。在内容上具有连续性,在理论研究范围上有所扩展,在术语翻译上有所改变,以及研究的深入等。
2.1 内容的连续
从《代数学》和《代数术》的目录可以看出二译著在内容上有着一定的连续性。《代数学》和《代数术》中都论述了方程理论、指数函数和对数函数的展开理论、级数理论等。并且《代数术》对代数理论的认识更清晰,在序言中指出“代数之术,其已知未知之数皆代之以字,而乘除加减各有记号以为区别,可以如题之曲折以相赴,适夫层累已明,阶级已见,乃以所代之数入之,而所求之数出焉,故可以省布算之工而心亦较逸。以其可不藉思索而得也。虽然代数之学诚简矣,诚便矣,试问工此术者遂能不病其繁乎,则又不能也。夫人之用心,日进而不已,苟不至昏眊迷乱,必不肯中辍。”[4]就是指出了代数方法,就是将已知数和未知数都用文字代入,主要指阿拉伯数字和一些英文字母来表示。而乘除加减各有符号以做区别,可以依照算题的式列挨次求解消除未知数,到了层次已分明,等式已见,就以所代之知列入,而所求之数就得出了。因此,可省去排列算式的工夫,而心里也比较轻松,因为代数公式可以不凭借苦思冥想而得。虽然代数学的确简明,的确方便,试问精于此学的人能不困于它的复杂吗?当然不能,人的脑力活动,天有进不已。如果不到老眼昏花迷乱时,必不肯中途停下来。人们继续进行代数研究,希望找到更好的解决方法,但是在寻找过程中可能会遇见更为复杂的代数问题,那么为了追寻新的问题就会诞生新的数学理论。可见,《代数术》中的内容是《代数学》中的内容的延续,这不仅仅是简单的延续,而且还有进一步的扩展。
2.2 范围的扩展
虽然《代数术》的内容是《代数学》内容的延续,但是在《代数学》的基础上有所扩展且内容更深更难。扩展内容中有关于连分数理,讨论连分数的及其运算。连分数中国传代数学中都已经出现过,但是在《代数术》中专门讨论连分数理论。有不定分析理论,专门讨论不定方程的求解问题。虽然中国古代传统数学中很早就有了不定分析,但是这种讨论不定方程正整数解的问题还是在一些简单方程上,比如勾股定理中的平方关系构成的方程,也是属于不定分析的范畴。然而,中国传统数学中对不定方程的研究相对简单。在《代数术》中有讨论解析几何问题,用代数方程解决几何问题。虽然《代数学》中出现一些三角函数公式,但是《代数术》中专门研究了三角函数及其运算,特别是关于三角函数展开理论。《代数学》中解决的一元一次方程和一元二次方程,相对来说比较简单。《代数术》中则出现了一元三次方程求解的卡尔达诺公式,并且还涉及了一元四次及四次以上的高次方程的求解。特变是其中关于一些高次方程的求解,通过变换或者转化,化成可求解的特殊方程,进而求出原方程的解。另外,《代数术》中非常重视计算问题,如级数计算中展开问题和经济学中的经济计算等问题。总之,《代数术》在理论上比《代数学》有很大的扩展,这不仅是表现在其内容体系上,更多的是在研究方法和蕴含的科学思想上,以及各领域的相互渗透。
2.3 术语的变化
比较分析《代数学》和《代数术》术语翻译,可以发现一些术语翻译的变化。比如关于“方程”一词的解释,二译著中就有一定的区别。《代数学》在第1卷中给出“并代数之几数名为式,二式之间作=号,谓之方程式”[2]在《代数术》第6卷中则有这样的描述“用代数术之本意,乃欲从已知之各数,求其未知之数。惟未知之数本与已知各数不相等,不得已将已知未知之各元,杂糅分合之,做一式令左右两边所代之数相等,谓之方程式。”[4]可以看出《代数术》中的这种表述更加的清晰,切合方程的本意。在《代数学》中的“同数”表示的就是未知数的“值”,而在《代数术》中将部分“同数”改为了“值”,并且认为“值者,本式所代之数也,亦名相当数。”可见,《代数术》给出了“值”的数学含义,指出了值就是代数式中所代表的数。此外,还有一些术语也类似发生了改变。对比分析《代数学》和《代数术》中的术语,可以发现后者的翻译更加严格和规范。并且,《代数学》不仅是继承了《代数学》在术语表述、公式、运算符号、分析作图等方面的内容体系,还发展和完善了前者的某些方面的表示。《代数术》的翻译出版,使得国人已经开始接受和认可了西方符号代数学的内容体系,这时中国传统代数学已经逐渐退出了中国历史的舞台。显然,西方代数学的引入更重要的是推进了代数西化的历史进程。
2.4 研究的深入
查阅代数学相关史料,可以发现在《数理精蕴》下编第31至36卷为《借根方比例》,其中讨论了建立和求解方程的问题。然而,18世纪初期的中国传统数学尚未具备接受近代西方符号代数的文化基础。在代数学的研究中,讨论代数方程根的问题时为了进一步研究方程的根与系数之间的相互关系,还须要有表示任意常数的符号,通过这种符号表示,使得建立的方程能更具有一般性。然而,在欠缺代数符号法则的情况下,采用传统表示法来研究代数理论及其相关问题,清代数学家汪莱(1768—1813)在这方面取得了较高成就,他能在“借根方”的基础上,迈出方程论研究的全新方向,为代数方程论与代数符号法则之间的关系,提供了一个可以赋予不同诠释的方向。《代数学》和《代数术》的出版使得中国数学家对中外代数理论的本质有了进一步的认识。在方程方面,不仅是方程次数越来越高,而且还讨论了根式可解性问题;级数不再只是讨论敛散性,还讨论收敛值问题;连分数问题、不定分析、经济计算和三角函数等问题都不再停留在某一个孤立的问题上,而是在不同领域的应用研究和一定的理论分析。
3 几个问题
通过对比可以发现《代数学》和《代数术》中有相同内容和不同内容,在相同的内容中,后者在其理论研究上有所扩展。特别是其中的几个数学问题使得近代西方代数学内容的引入具有更高的理论性。特别以卡尔达诺公式、高次方程解法、连分数问题和不定分析为代表的几个问题,为后来的代数学研究提供了新的方法和方向。
3.1 Cardano公式
关于代数方程根式可解性,指的是对于代数方程有根式解。n次多项式方程有代数表达式为
a0xn+a1xn-1+…+an-1x+an=0






3.2 解高次方程

不管是从代数方程根式可解性,还是用构造法来解决高次方程,《代数学》和《代数术》都没有详细去论述根式可解性的代数学原因。即方程根式解是一个著名的古典代数学问题,域F上次数大于1的多项式f(x),若方程f(x)=0的每个根都可由f(x)的系数经过加、减、乘、除及开方运算得出,则称f(x)=0有根式解。换言之,f(x)的分裂域含于F上一个根式扩域,次数大于或等于5的代数方程是否有根式解,这一代数学问题,直到19世纪30年代才得到解决。法国数学家埃瓦里斯特·伽罗瓦(Évariste Galois,1811—1832)用群论系统化地阐述了五次及五次以上方程不能用公式求解的原因[9]。对于一些特殊的五次及五次以上代数方程则可以根据一些变换或者转化成可以求解的方程得以解决。
伟烈亚力不仅对西方代数学发展史有所了解,通过与中国学者的交流和查阅中国历史文献,对中国代数学发展史也有一定的研究,特别是中国传统数学中的“天元术”,并且对“天元术”作出了相关论述和研究[10]。中国传统数学中深入没有讨论根式可解问题,但是有解高次方程的一些方法。中国传统数学中很早就出现了高次方程的解法,比如朱世杰及其《四元玉鉴》中出现了关于首先用天元术建立了代数方程,然后再用增乘开方法解其根。在其相关计算中出现了两个方程,将两个方程联立后的一方程组,把要求解的值转化为求出方程组的解:

3.3 连分数问题
连分数很早就出现在中国传统历法计算中,连分数运算是为了解决历法计算中的一些问题。所谓连分数就是一种特殊类型的繁分数,将一个分数经过多次的运算最终化为如形式:
《代数术》第20卷就专门论述连分数相关问题,特别讨论了分数和连分数之间的转化,其中有“凡数之可以平常之分数明之者,亦能以连分数明之。”[4]其中第188款介绍了分数与连分数的相互转化,第190款论述了“循环连分数”,第191款讨论了将无理数化为连分数等问题。《代数学》中出现的是基本的分数运算,而在《代数术》中则出现了连分数运算,特别是把分数运算理论和无理数理论联系起来。连分数形式有什么意义,对于古人来说,连分数有一个优点是其它简单分数无法做到,那就是无限逼近,即求近似值。古希腊人发现了平方等于2的一个方程,其解相当于开平方,但是这个2的平方根具体等于多少,却没有办法用整数或者简单分数来表示,这就要通过循环代换后,用连分数来表示,通过截取其中任意一段连分数,可以求出该平方根的近似值。而且,发现其不能用有简单分数表示出来,只能用连分数表示,这就是数学史上无理数的起源。古希腊人就是这样做到徒手开平方的,这对求解一些无理数最佳逼近等相关问题提供了方法和思想。《代数术》中的连分数运算涉及到了很多方面,对数学及相关科学的发展,提供了运算上的理论支持。
3.4 不定分析
中国传统数学中很早就出现了不定分析,《九章算术》中的勾股定理问题就是最早的不定分析问题之一[12-13]。中国古代的著作《张丘建算经》中的“百鸡问题”就是较早的讨论不定方程求解问题,属于不定分析领域的研究。其中求解问题,相当于求解一个不定方程组:
该著作中给出了答案为三组解,第一组解为X=4,Y=18,Z=78,第二组解为X=8,Y=11,Z=81,第三组解为X=12,Y=4,Z=84。对于这三组解是怎么求解出来,该著作中没有给出求解的过程。《张丘建算经》中的“百鸡问题”出现后,数学家甄鸾(535—566)和李淳风(602—670)进行了注释,但都没有给出详细的求解过程。到了宋元时期,数学家遇见到了更为复杂的不定分析,并且对不定分析有了深入的研究。宋元四大家在代数方面的贡献,还表现在他们所创立的同余理论,特别是以“中国剩余定理”为代表的不定分析理论。中国传统数学中给出了一次同余方程:
x≡r1(modm1)≡r2(modm2)≡…≡rn(modmn)

4 相关计算
不管是从代数研究的内容上,还是从代数理论的难易程度上,从《代数学》到《代数术》都发生了一定的变化。代数运算从前面的纯粹的数学运算变为实际生活中的计算,特别是生活中的经济计算等问题。级数运算从前面的只讨论敛散性,发展为级数的收敛值,收敛半径和收敛区间等问题上了。另外,三角函数的出现不再是为了纯粹的计算问题,而是应用于实际生活之中,以及在各种数学问题中的应用。
4.1 经济计算
华蘅芳在《代数术》的序言中指出“观夫市廛贸易之区,百货罗列、精粗美恶贵贱之不同,则其数殊焉。多寡长短,大小轻重之不同,则此数又殊焉。凡欲与所有易其所无者,必据算而计之,其所斤斤计较者,莫非数之。设有人言吾能以他法以代其数,谁能信之。良以乘除加减不过举手之劳,顷刻而得,无有奥邃难明之理在其间,本无藉乎代也。惟是数理幽深,最耐探索,畴人演算,务阐精微,于是乎设题愈难,布算愈繁,甚至经旬累月不能毕。一数且其所求之数往往杂糅隐匿于各数之内而其理亦纡远而不易明。若每事必设一题,每题必立一术,枝枝节节而为之术之多将不可胜记而仍不足以穷数理之变,则不如任数理之万变而我立一通法以驭之。此中法之天元,西法之代数所由作也。”[4]可以看出在贸易市场上,陈列着各种各样的货物。由于精粗、美丑,物品的等级不同,所以价格也各有不同。多少、长短、大小、轻重的不同,按照一定的比例所计算的价钱又不同。凡是想以你所有的物品去交换你所没有的物品,这其中必然要根据算来计数,通过相关计算你才会获得一个可靠的数据,这样也就显得公平。这说明代数运算在经济生活中的重要性,如果没有运算,那么就很困难。在第19卷中“论生息计利”就是讨论各种借贷中有关利息算法,涉及单利和复利等问题。《代数术》中有两种利息计算方法,第一种是“简利息法”,即按照利息与本金之间的比例来进行计算。第二种利息计算法则是“繁利息法”,指出这是“将其所得之利添入本金之内”,这就是利息加入本金后再算利息,即利翻利或利滚利。在第180款中给出了计算利息的参数为本金、本金所产生的利钱、本金所消耗的时间、本金和利息的总和,这四个参数决定了利息计算。最后,还提及了“保险之事”,但是认为其“算理极深”,故而没有进行论述和研究。可以看出,《代数学》中没有涉及到经济科学,而在《代数术》中涉及到了经济计算,这可以看出《代数术》是在《代数学》的基础上,增加了生活实践的应用问题探究。在《代数术》的序言中就给出了“不如极之于九而以十进其位,则举手而示,屈指而记,虽然愚鲁者皆能之,故可便于民生日用,传至数千百年至今不变也。”的表述,认为代数运算可以简化运算的繁杂程度。
4.2 级数运算
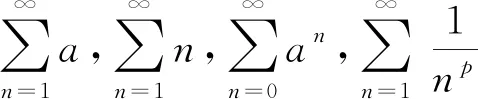

在《代数学》中的级数敛散性初步理论基础上,《代数术》引入了更为复杂的级数理论。在《代数术》第18卷和第25卷中论述了级数的收敛速度和收敛区间等问题。同时,还给出了函数的级数展开式。如y=ax,用y表示x的无穷级数为
x=

logay=
4.3 三角函数
三角函数及其代换在《代数术》中出现,用以解决诸多运算问题。《代数术》第24卷和25卷介绍了三角函数及其相关应用问题。在第24卷中的一开始就介绍了三角函数理论的发展史,接着介绍了余角、外角、余弧、外弧等。第225款讨论了正弦和余弦在坐标系中各个象限的符号,何时为正何时为负。还给出了正切、正切线、余切、余切线、正割、正割线、余割、余割线等定义,还给出了正矢和余矢等概念及其数学运算。在第232款中三角函数的“诱导公式”,给出了各三角函数之间的相互转化。第236款讨论了三角函数的定义域,分析了三角函数自变量的取值范围。随后各款讨论了任意两角之和差的正弦与余弦推导并给出了相应的公式。第25卷就对前一卷的三角函数理论进行了实际应用分析。
可以看出《代数学》中的三角函数在于去求三角函数的值,而《代数术》中的三角函数更多的是去解决实际应用问题,通过应用问题的求解反过来寻找三角函数的理论意义。另外,还可以把三角函数的运算与求解方程结合在一起,解决求解方程方面的一些困难,这正是三角函数理论进一步应用于实际数学问题的表现,同时,这些应用问题也是三角函数理论得到更进一步深入研究。
5 后续影响
显然,不管是李善兰和伟烈亚力合译的《代数学》,还是华蘅芳和傅兰雅合译的《代数术》,二者对清末科学研究和科学教育都有着深刻的影响。特别是作为数学家的李善兰,他不仅和西方学者合作翻译出版西方数学著作,他自己还出版数学著作,并且,他在同文馆作为算学教习教授数学时,还经常与馆内学生研讨各种数学问题,与当时的数学家交流数学问题,这本身对清末的科学和教育就产生了直接的影响[15-19]。在数学译著的翻译过程中对语言的表述也有着一定的影响,特别是《代数学》和《代数术》中有的数学术语发生了演变,有的术语则赋予了科学的数学涵义。正如当代学者潘文国认为“强调为人先于为译,主张一切翻译都要在完整传达原本意义的基础上进行文字加工”[20]。这就需要译者对数学理论本身的掌握,才能表述出科学的理论。在这方面,清末翻译家在翻译西方数学著作时对名词术语的厘定发挥了重要的作用[21]。华蘅芳不仅和西方学者合作翻译出版西方数学著作,自己对数学也有深入的研究。当然,这种影响有大小之分,有直接和间接之别。李善兰和伟烈亚力翻译出版《代数学》后,国人对代数学理论的研究不多。首先,是中国传统代数学在清末时期没有得到更为较好的发展。在《代数学》出版后,没有更多以“代数”或者“代数学”相关的词汇为名的代数学著作。而在华蘅芳和傅兰雅翻译出版《代数术》后,相关代数学著作相继引入并出版发行。如后来出版的著作《三角数理》(1877)、《代数难题解法》(1879)、《算式要法》(1899)等都受到其影响。当然,这种影响也是二译著都有的,只是一个相互影响且循序渐进的过程。另外,随着清末代数学方面的著作或译著的出版,清末各种学堂中开始开设代数学课程,同时在各种考试的试题中出现了代数学相关理论。可见,《代数学》和《代数术》对清末的教育有着很深的影响。中国在传统代数学理论有着光辉的成就,宋元之后发展缓和下来[22]。当《代数学》为中国引入了符号代数后,接着《代数术》中的高次方程求解问题则引入了给为高深的代数学理论。从《代数学》和《代数术》之后诸多代数学著作的相继出版,可以看出二译著对中国传统代数学的嬗变和西化作出的贡献,以及对清末科学和教育的深远影响[23]。清末综合性杂志《中西闻见录》于1873年刊载了刘业全的《立天元一源流考》[24]和艾约瑟(Joseph Edkins,1823—1905)的《阿尔热巴喇源流考》[25],中西学者对代数学历史进行论述。于1875年在第36号上发表中国学者殷仲深的《弧弦设题》就涉及到了三角函数计算及其应用问题的研究[26]。在《中西闻见录》中,相关的论文中涉及到了代数和几何方面的研究,还有代数和几何的综合研究等[27]。清末数学家陈志坚和华世芳(1854—1905)对连分数的研究等[28]。这些都可以看出二译著对清末科学和教育的影响。译著不仅对清末科学与教育产生了深远影响,而且还传入日本,促进了日本和算的西化[29]。中国传统数学中的一些理论,从早期诞生以来都还有着研究的生命力。勾股定理从“商高问答”的出现,一直到清末数学家都还在研究其代数运算关系。其中把数学由经验发展为推导证明的层次,以此奠定了中国传统数学理论的基石[30]。纵观西方微积分发展史,中国早期的极限思想,以及后来李善兰的无限分割求和思想与西方微积分思想在本质上有着异曲同工之妙[31]。通过分析中外历史文献,可以看出其理论的基础。中西在代数学理论上也如此,所以,伟烈亚力还把中国传统代数学理论及其历史介绍给了西方学者,特别是《九章算术》为代表的代数理论、“大衍求一术”、“天元术”和“高次方程数值解”等内容[32]。与此同时,还结合中西代数学发展史给予了科学的评价。从科学发展的历史来看,不管是西方科学还是中国传统科学,任何历史发展阶段,科学理论总是源于社会与自然,其思想之源是社会和自然,在其中发现相关理论,并在实践中得到检验和逐步发展[33]。不管是“师夷长技以自强”思想还是“中学为体,西学为用”思想,这些都强调了学习西方先进科技的重要性[34]。在《代数学》和《代数术》之前,西方代数学理论已经开始传入我国,并且得到了一定的发展。随着二译著的翻译出版,代数理论得以系统地引入,同时得到了更高水平的发展。并且,随之而来的是更多代数学著作的出现。影响着后来代数学的发展,并且一直影响至今。正如吴文俊先生分析中西方在代数学领域的发展模式和理论研究水平等问题后,他指出近代数学能够发展至今主要是靠中国传统数学思想[35]。当然,决定数学发展历史进程的是中外数学思想的总和。并且,中西方数学的融合使得中西方的数学思想相互影响和发展。
6 结 语
作为清末的两部经典代数学译著,《代数学》和《代数术》相继引入了近代西方代数理论。二者有着承前启后的相互关系。在内容上具有一定的连续性,在理论研究范围上得到了进一步的扩展,翻译术语及其表示上有所改进,研究的层次进一步深入等。通过比较分析可以得出《代数术》引入的代数理论要比《代数学》中的更深更难。特别是其中的卡尔达诺求根公式、高次方程解法、连分数及其运算、不定分析等内容。另外,《代数术》中的相关计算问题也很重视应用性,体现在经济领域的计算,复杂的级数展开,三角函数及其应用等。《代数术》在《代数学》的基础上,不但理论层次有提高,更重要的是其强调理论的应用性。同时,这些应用问题不仅表现在数学领域,而且还渗透到其他科学领域。因此,这样的学科渗透深深地影响着其它科学的发展。一前一后的两部译著对清末科学与教育有着深远的影响。特别是其中的几个相关问题对后来中国学者学习和研究西方代数理论提供了素材和指明了方向,也为中国代数学的西化和引入抽象代数奠定了理论基础。

