关于连续原根的分布
刘华宁, 景梦谣
(西北大学 数学学院, 陕西 西安 710127)

命题1(Szalay)设p为素数,并定义
M(p,l)=#{x:x∈Gp,…,x+l-1∈Gp}。
则有
其中d(p-1)表示p-1的正因数的个数。
Tanti和Thangadurai[10]改进了上面的结论。
命题2(Tanti和Thangadurai) 设l≥2为正整数。 则对任意素数p≥e25.54l,都存在模p的l个连续原根。
此外,设A,B⊂Zp,A∩B=∅,I={M+1,M+2,…,M+N}⊂{1,2,…,p},并设N(A,B,p,I)表示I中使得对所有a∈A都有n+a∈Gp,以及对所有b∈B都有n+b∉Gp的n的个数。Cobeli和Zaharescu[11]证明了
Cohen等人还考虑了在一般有限域中的情形[12-16]。
1 主要结论
本文将给出上述结果的一些推广。主要结论如下。
定理1设p为素数,f(x)∈Fp[x]的次数为D≥1。l1,l2,…,lk是Fp中互不相同的元素。定义
M(f,l1,…,lk;p)=#{n:1≤n≤p,f(n+l1)∈Gp,…,f(n+lk)∈Gp}。
假设下列条件至少满足一个:
(i)f(x)不可约;


则有
其中ω(q)表示q的不同素因子的个数。
推论1设p为素数,f(x)∈Fp[x]的次数为D≥1。设整数k≥2,并设l1,l2,…,lk是Fp中互不相同的元素。 假设下列条件至少满足一个:
(i)f(x)不可约;


则对任意素数p>max{e23k,(kD)27},都存在n∈Fp,使得
f(n+l1),f(n+l2),…,f(n+lk)
都是模p的原根。
定理2设p为素数,A,B⊂ZP,A∩B=∅,I={M+1,M+2,…,M+N}⊂{1,2,…,p},f(x)∈Fp[x]的次数为D≥1。设N(A,B,I,f;p)表示I中使得对所有a∈A都有f(n+a)∈Gp,以及对所有b∈B都有f(n+b)∉Gp的n的个数。假设下列条件至少满足一个:
(i)f(x)不可约;


则有
2 多项式特征和的估计
我们需要下面的一些引理。
引理1设f(x)∈Fq[x],d|q-1,χ为Fq的d阶非主特征。设f(x)≠a·hd(x),a∈Fq,h(x)∈Fq[x],且f(x)在其分裂域内有t个不同的根。则有
证明见文献[17]第43页。
引理2设p是一个素数,χ是模p的d阶非主特征。设f(x)∈Fp[x]且f(x)≠a·hd(x),其中a∈Fp,h(x)∈Fp[x]。设s表示f(x)在其分裂域内不同根的个数,实数X,Y满足0 证明见文献[17]第51页。 h(x)=fδ1(x+l1)…fδk(x+lk) 假设下列条件至少满足一个: (i)deg(f) (ii) (4k)deg(f) 则h(x)不能表为任何多项式的d次幂的常数倍。 证明参阅文献[18]。 注意到 (1) M(f,l1,…,lk;p)= M1(f,l1,…lk;p)+M2(f,l1,…lk;p)。 (2) 容易证明 (3) 另一方面,设ψ为模p的特征群的生成元,可得 M2(f,l1,…lk;p)= (4) 情形1假设f(x)不可约。显然 是p-1次幂的常数倍当且仅当 由于d1…dk>1,因此上式不成立。则由引理1,有 |M2(f,l1,…,lk;p)|≤ (5) (i)D (ii) (4k)D 则由引理3可知 不可能是p-1次幂的常数倍。再由引理1可得 |M2(f,l1,…,lk;p)|≤ (6) 现在结合式(2)~(6)立得 这就证明了定理1。 接下来证明推论1。根据定理1,有 M(f,l1,…,lk;p)≥ 此外由文献[19]中的167页可知,对所有素数p≥5都满足 设p>max{e23k,(kD)27}。容易证明 M(f,l1,…,lk;p)>0 ⟸logp>2log(kD)+2klog2·ω(p-1) 上式成立,从而证明了推论1。 现在证明定理2。首先考虑特殊情形B=∅,此时A不为空集。记A={a1,…,as},则有 N(A,I,f;p)= N1(A,I,f;p)+N2(A,I,f;p) 。 (7) 容易证明 (8) 另一方面,设ψ为模p的特征群的生成元,可得 N2(A,I,f;p)= 由引理3可知 不可能是p-1次幂的常数倍。再由引理2可得 N2(A,I,f;p)≤ (9) 现在考虑一般的B。记 可得 N(A,B,I,f;p)= (10) 再由式(8),有 (11) 另一方面,由式(9)可得 N2JB(A∪C,I,f;p)≤ (12) 因此, (13) 此外还有 9|A∪B|D (14) 结合式(13)和(14)立即可得 定理2证毕。
3 定理1和推论1的证明




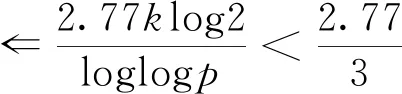

4 定理2的证明




