基于耦合模型的电容法两相流相含率测量性能分析
王小鑫, 胡红利, 唐凯豪, 陈阳正, 蒲俊萍
(1.西安石油大学 陕西省光电传感测井重点实验室, 陕西 西安 710065;2. 西安交通大学 电力设备电气绝缘国家重点实验室, 陕西 西安 710049)
两相流普遍存在于石油、化工、制药、电力、环保、冶金等现代工业领域中,两相流参数检测技术在科学研究和工业生产中发挥着越来越重要的作用[1-3]。两相流参数主要包括相含率、流速、流型及压力等,其中,相含率是最主要的检测与控制参数,尤其是多相流中某一相或者某两相的实时流量对工业过程监控是十分重要的。电容法作为两相流参数测量常用方法之一,具有成本低、结构简单、无侵入、灵敏度高等优点。电容法测量相含率的原理是,当两相流的各相含率发生变化时,管道截面等效介电常数也发生变化,导致电极间电容值发生相应变化[4]。
常用的电容传感器主要有对臂结构、螺旋结构和双环结构[5-8],针对不同的应用对象和工作条件,学者们通常采用静电场仿真和静态试验的方法来评估传感器的性能,进而选择合适的传感器结构。彭黎辉[6]使用有限元方法对以上3种传感器结构建立三维静电场模型,首先,通过静电场分析了不同传感器的灵敏度分布特性,然后,设计了基于快速关闭伐法的试验平台来验证相含率测量,结果表明在该测量环境下,相比于对壁式传感器,螺旋传感器具有更高的灵敏度及更加均匀的灵敏度分布。Abdullah 和Zareh[7]通过静态试验对这3种传感器进行了研究,用非流动的空气、石蜡、玻璃、木材等模拟相含率,并得出结论:螺旋传感器具有低灵敏度,因此不适合精确的相含率测量,对壁式的灵敏度最高,而双环式的灵敏度居于另外两种之间。Emerson和Diego[5]同样设计了上述3种类型的传感器,并使用空气和去离子水在层流状态下对传感器分别进行了静态试验,结果显示双环式是最适合用于测量上述对象的传感器类型。
通过以上文献的分析,首先,可以得出传感器的结构决定了测量系统的性能;其次,对于同一种类型的传感器,在不同应用对象、不同试验环境及不同结构尺寸下,它们所表现的性能有很大不同。在以往的研究中,通常采用静电场灵敏度分布仿真分析和大量的实测试验来评价传感器性能,然而,静电场仿真只能研究传感器的静态电学特征,并不能结合实际的多相流流动特性。对于试验验证,它需要消耗大量的人力、物力及时间来应对不同对象及应用条件。针对以上问题,王小鑫[8]等人提出一种流场电场耦合的三维动态仿真模型,对螺旋式、对臂式、双环式传感器进行了性能评估,并通过试验验证了该模型的有效性。本文将在以上耦合模型的研究基础上,分别对2电极、4电极及8电极阵列式结构在气固两相流相含率测量方面的性能进行评估,并搭建气固两相流相含率测量试验平台,对3种传感器测量性能的仿真结果进行验证。
1 耦合模型原理
由静电场的拉普拉斯方程及狄利克雷边界条件可得[9]
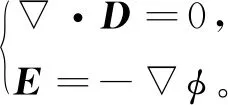
(1)
D=ε0εrE。
(2)
其中:D是电位移;E是电场强度分布;φ是电势;ε0是真空介电常数;εr是混合物的相对介电常数。
两相流场中,采用欧拉-欧拉瞬时模型来描述气固两相流实时动态流动。模型由连续性方程和动量方程表示。
连续性方程为
(3)
其中:φc是连续相的含有率;φd是离散相的含有率,且φc=1-φd;ρc是连续相的密度;ρd是离散相的密度;uc是连续相速度;ud是离散相速度。
动量方程为
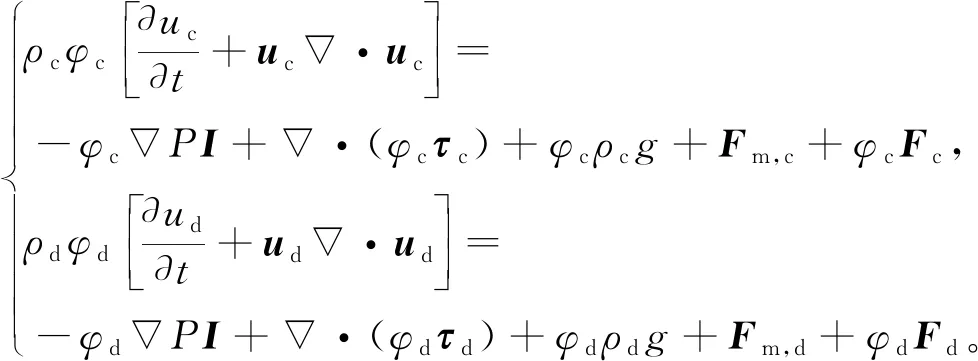
(4)
其中:P是混合相的压力;τc是连续相黏性应力张量;τd是离散相黏性应力张量;g是重力加速度;Fm(Fm,c及Fm,d) 是两相之间的相互作用力;F(Fc及Fd) 是体积力[10-11];I是单位向量。
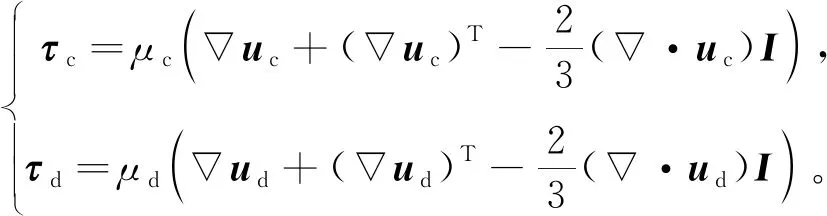
(5)
其中:μc是连续相的动态黏滞度;μd是离散相的动态黏滞度。
本文建立的三维耦合模型中,F是电场力,表示为[12-13]
F=·T,
(6)
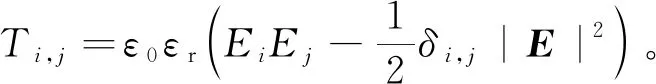
(7)
其中,δi,j是克罗内克符号,
T=ε0εr·
(8)
混合物的相对介电常数εr可以由Maxwell-Garnett方程表示为
(9)
其中,εd和εc分别是固体(离散相)相对介电常数和气体(连续相)相对介电常数,该公式是耦合模型成功建立的关键。
2 耦合仿真
2.1 仿真条件
这里利用COMSOL Multiphysics多物理场仿真软件对模型进行数值仿真,并在Matlab中进行数据处理。耦合模型包括Euler-Euler湍流模型(流体场)及AC/DC模块(静电场)。耦合场的主要物理参数见表1,这里的仿真环境参考燃煤电厂气力输送系统中气固两相流的相含率测量。基于该耦合模型研究了3种电容传感器结构 (2个电极、4个电极和8个电极),电极片等间隔安装在石英玻璃管周围,电极片之间间隔连接,实际均等效为两电极结构,其参数如表2所示。
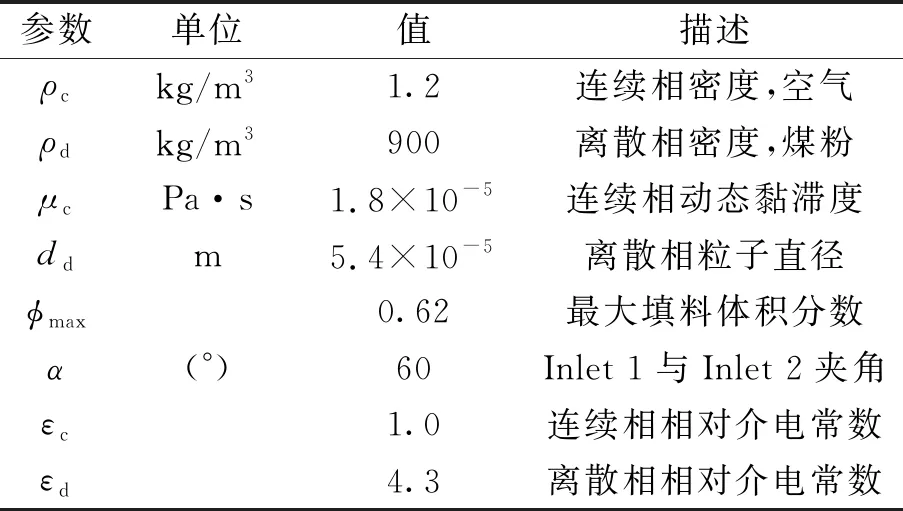
表1 耦合场主要物理参数Tab.1 Physical parameter of the coupled field

表2 3种电容传感器参数Tab.2 Parameters of the 3 capacitive sensors
2.2 基于耦合模型的传感器的性能分析
图1为建立的气力输送管道及传感器的耦合仿真模型,入口1是空气入口,入口切向速度为10m/s,入口2是固体颗粒给粉入口,入口切向速度为2m/s。输送管道直径D=100mm,给粉管道直径40mm。传感器安装在l=800mm处,l为入口1到电极中心的距离。
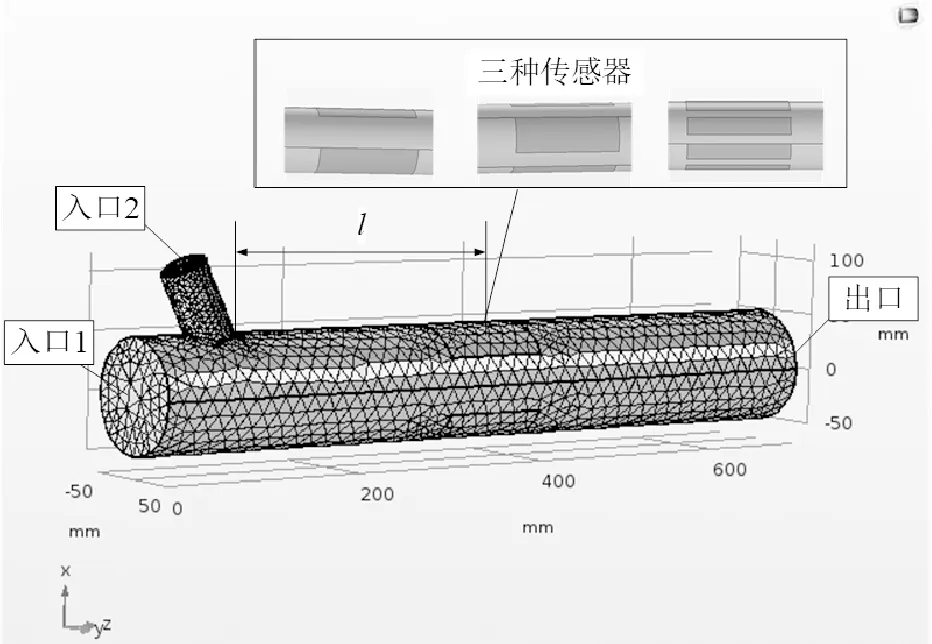
图1 管道及传感器仿真模型Fig.1 The simulation model of pipeline and sensor
入口2的给粉相含率(体积分数)p与出口的固相体积分数vout的关系曲线如图2所示,该值由动态流场仿真得出。在实际的燃煤火电厂应用中,煤粉与空气的固气质量比通常在0.1~1之间,相应的煤粉体积浓度范围通常为0.1‰ ~ 1.5‰,因此,本文仿真过程中参数p分别取值0.01,0.02,0.03,0.04,0.05,共5个点。
耦合模型针对每个测量点运行3s,以0.1s为步长,记录每个相含率测量点的31组数据。图3中分别提取第0.6s, 0.9s, 1.2s, 1.5s, 2s和3s时传感器中心横截面上的离散相体积分数分布情况,其中图例中的颜色条范围保持一致。
从图3中可以看出0s到1.2s之间的流型不稳定,称之为过渡过程;1.5s到3s之间的流型比较稳定,稳定后的流型主要为层流。基于动态气固两相流耦合模型的建立, 相应电极对之间的电容值可以由模型输出。图4、图5、图6分别是2电极、4电极、8电极的电容值变化趋势,及其稳定状态下的电容平均值(取1.5s之后的电容平均值)。
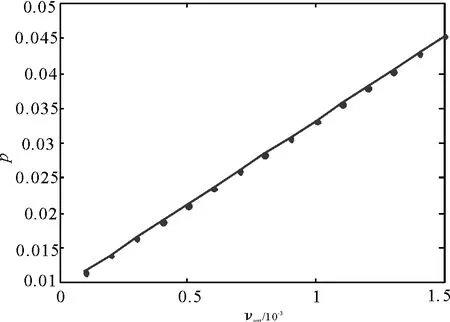
图2 p与vout之间的关系曲线Fig.2 The relation curve between p and vout

图3 离散相的体积分数分布Fig.3 The volume fraction distribution of dispersed phase
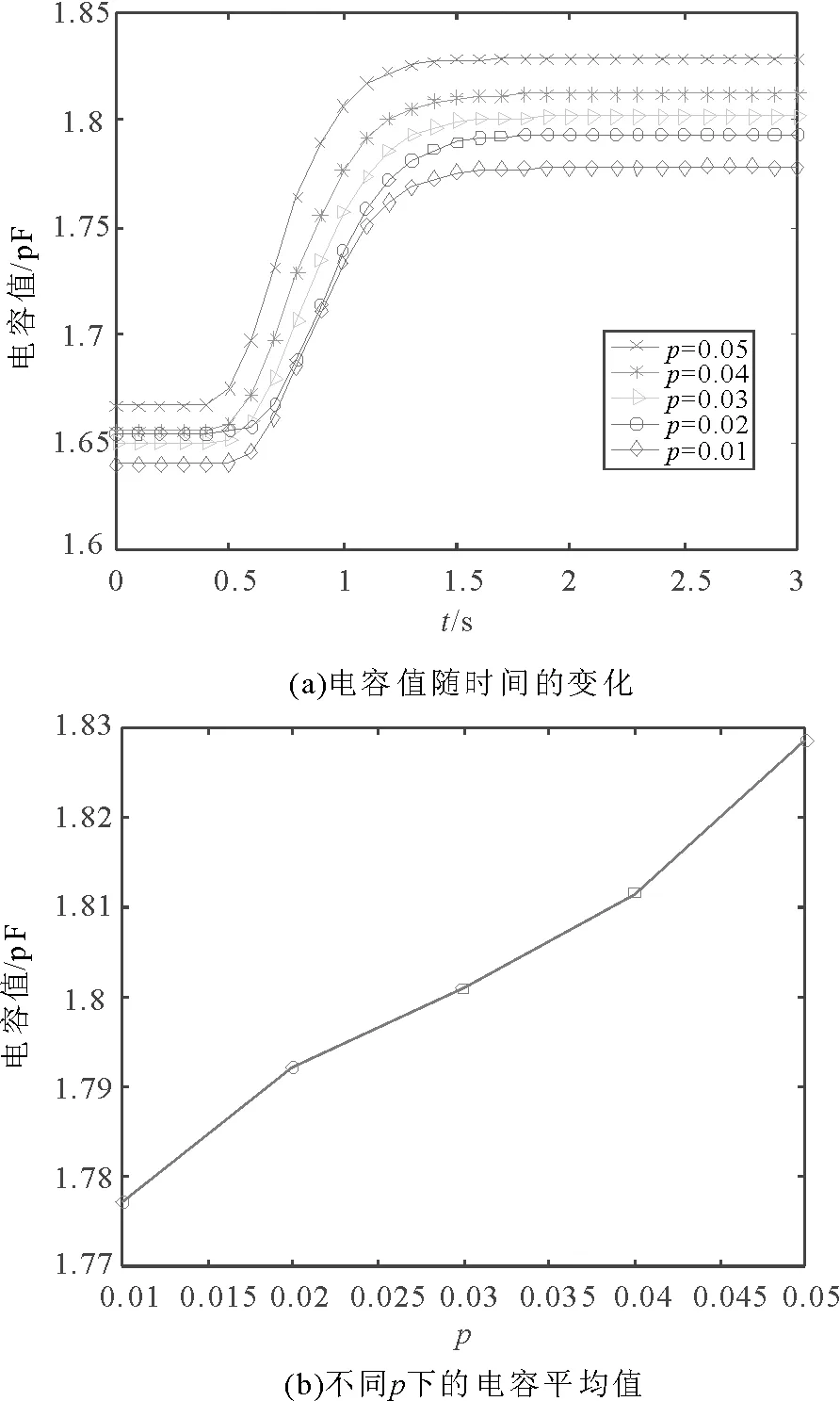
图4 2电极Fig.4 2-electrode
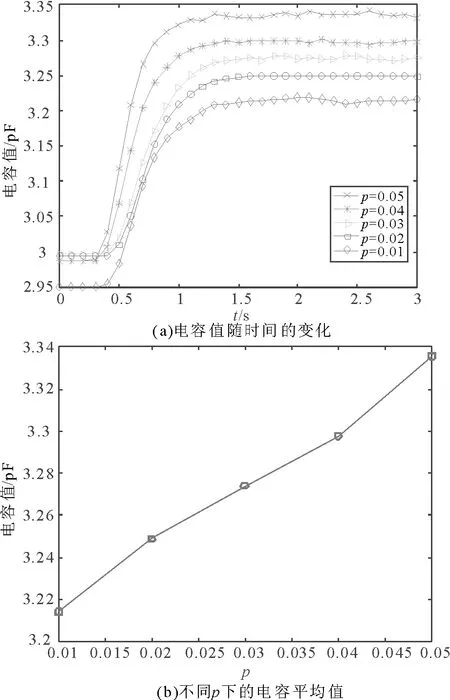
图5 4电极Fig.5 4-electrode
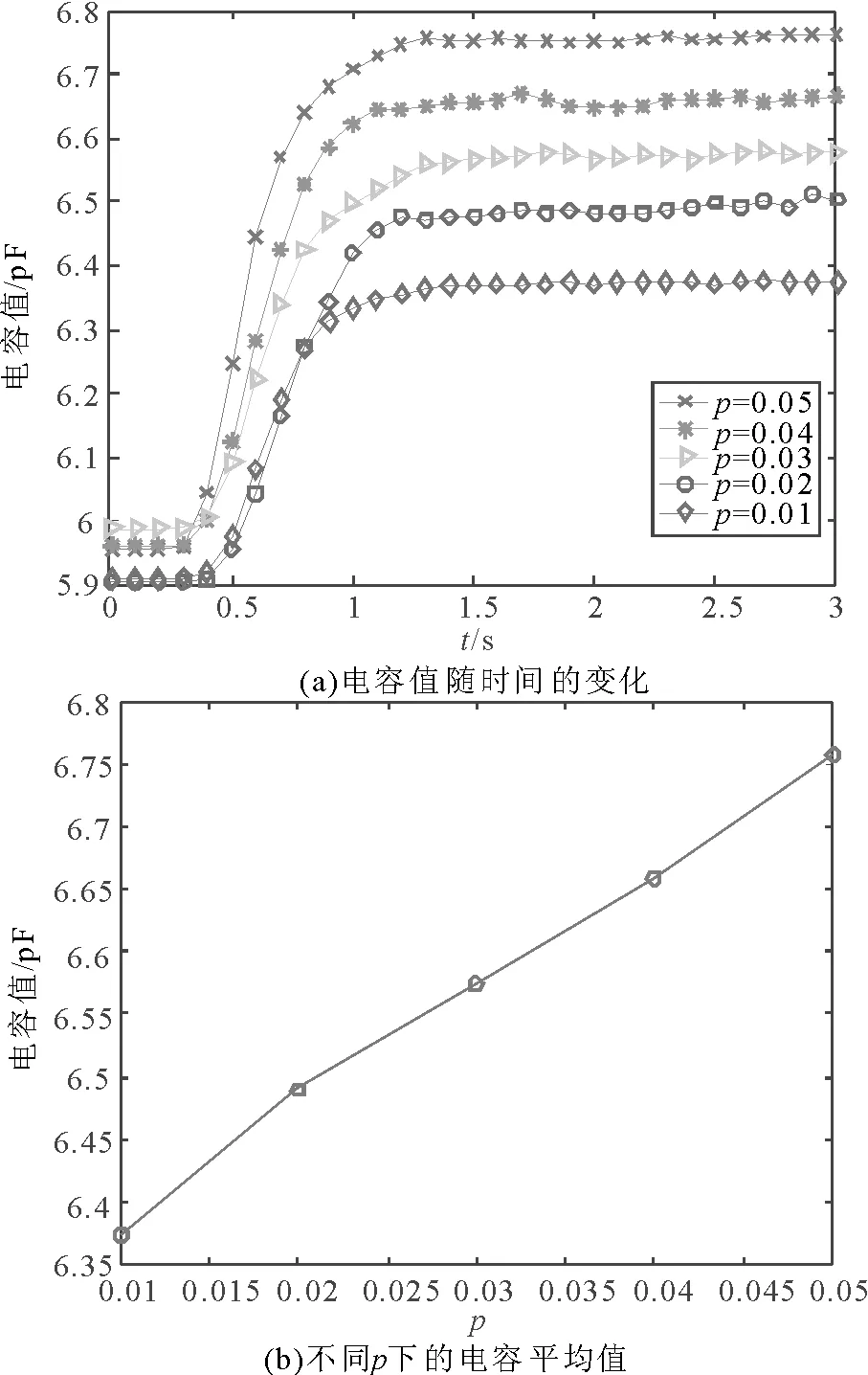
图6 8电极Fig.6 8-electrode
从图4(a)、图5(a)、图6(a)中可以看出,测量点的曲线在0~1.2s之间不平稳,大概在1.5s之后均趋于平稳,这与图3中固相体积分布图趋势一致。这里采用线性相关系数和灵敏度均值来评价传感器的性能。线性相关系数是一种通过将两个变量的协方差除以其方差乘积的平方根来衡量两个变量之间的相关程度的统计量。其值越接近1或者-1,说明相关性越强,反之越接近0,说明相关性越弱。线性相关系数r可以表示为
(10)
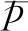

表3 线性相关系数rTab.3 Correlation coefficient r
从表3中可以看出,仿真环境下3种电极结构的测量电容值与相含率之间均具有较好的相关性,其中,4电极的相关性最高,r=0.98, 其次是8电极,r=0.95, 最低的是2电极,r=0.93。
系统灵敏度均值S可以表示为

(11)
表4列出了3种电极结构的灵敏度均值,可以看出,随着电极数的增加,其系统灵敏度均值增加。为了验证该耦合模型的有效性,下面将在气力输送实验平台上对该系统进行验证。
3 试验验证
图7所示的气力输送系统用于验证以上耦合模型的仿真结果,该平台包括载气单元、给粉单元、测试单元、收集单元。
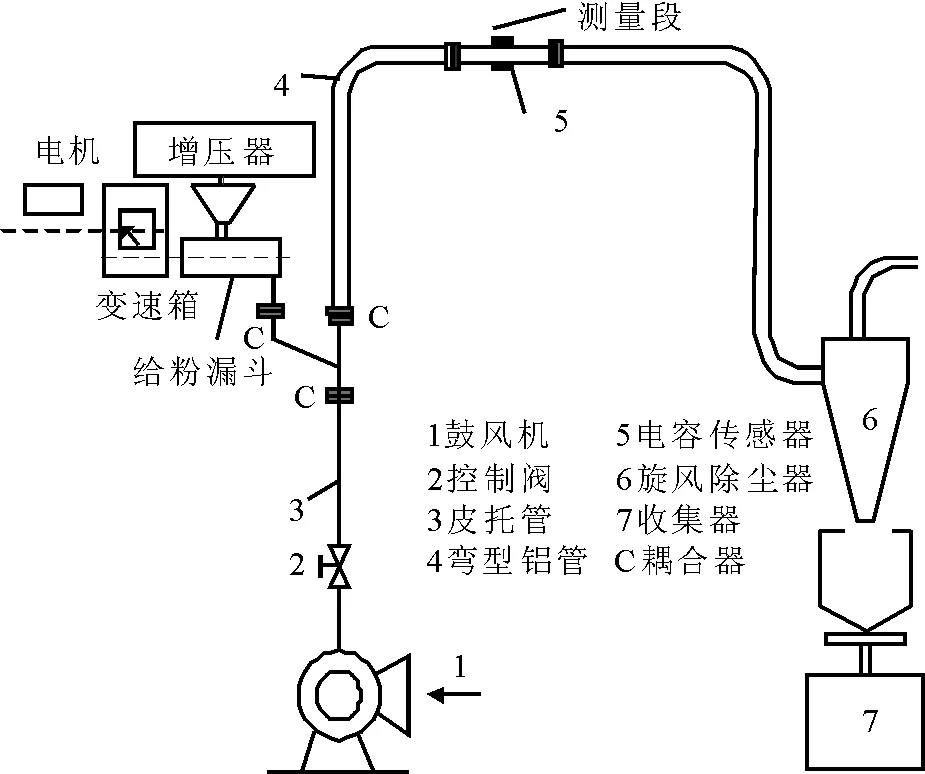
图7 实验平台Fig.7 Experimental platform
气固两相分别为空气和煤粉,载气速度为10m/s,给粉量范围12.82~54.22g/s,根据相含率与质量流量、风速之间的关系[14],可以求得相含率的范围为0.100 6×10-3~0.426 3×10-3。测量段为长度为1 200mm的透明石英玻璃,直径为100mm。电容测量电路采用激励频率为5MHz的交流激励C/V电容电压转换电路,并通过以ARM Cortex-M4为架构的STM32F407ZGT6芯片对输出信号进行采集和处理[15-16]。3种传感器结构与仿真模型的结构参数一致。
在每种相含率下,采集10组稳定状态下的电压测量值,并取平均值,图8为3种传感器在6种不同相含率下的电压测量值曲线。表5为实测环境下传感器的性能参数。
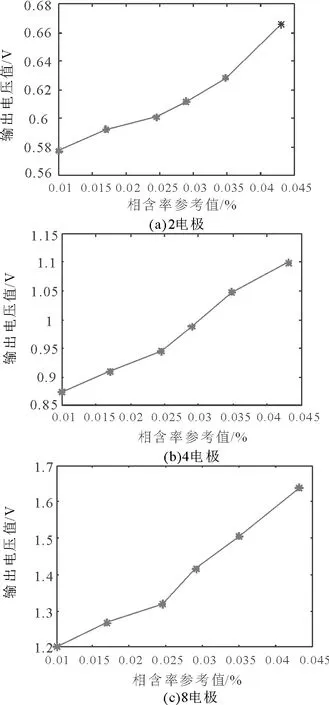
图8 测量曲线Fig.8 Measurement curve
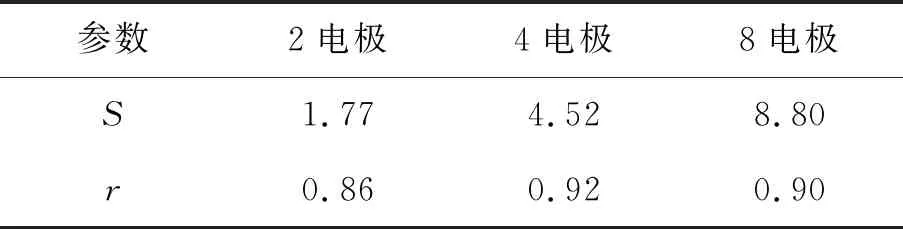
参数2电极4电极8电极 S1.774.528.80r0.860.920.90
从图8及表5中可以看出, 随着电极数的增加, 系统灵敏度S依次增加, 8电极的最大,S=8.80,2电极的最小,S=1.77。对线性相关系数而言,4电极的相关系数最高,r=0.92,其次是8电极,r=0.90,最差的是2电极,r=0.86。相比于耦合仿真条件下的测量特性,实测环境下的测量特性相对较差。这主要是因为在仿真条件下,设定了一些假设或者理想条件,例如粒径均匀、给粉均匀,并且流体在仿真状态下的流动是相对稳定的,不受外界因素影响。然而,在实际测量过程中,受干扰因素较多,例如风速、粒径及给粉机稳定性等。无论是仿真还是实测环境下,3种传感器的测量特性的变化趋势是一样的。因此,基于耦合模型的性能评估与实际相含率测量得到的性能评估结论基本上是一致的,即该耦合模型对于实测过程中的传感器性能评估是有效的。
4 结 论
本文提出了一种三维动态仿真手段耦合静电场及流体场,用于电学法多相流参数测量的传感器性能评估。在该耦合模型的基础上,通过对不同传感器测量结果的灵敏度、相关系数的量化分析,以评估不同结构的电容传感器用于气固两相流相含率测量的性能。为了验证该耦合模型方案的有效性,搭建了气固两相流相含率测量平台,对仿真过程中使用到的3种传感器结构分别进行了试验验证,试验结果表明,耦合模型的性能评估与实际相含率测量得到的性能评估基本上是一致的,即该耦合模型对于实测过程中的传感器性能评估是有效的。该耦合模型同样可以为多相流的流速、流量测量及ECT/ERT电学层析成像等应用提供传感器优化选型、算法优化等方面的仿真指导意见。

