压缩感知在ECT分相含率检测中的应用
唐晨晖,胡红利,王 格,张 肖
(1.西安交通大学 电力设备电气绝缘国家重点实验室,陕西 西安 710049;2.西安市产品质量监督检验院,陕西 西安 710065)
多相流作为一种混合流动体系广泛存在于自然界和工业生产中,尤其在电力、石油、化工、冶金、航空航天等关系到国计民生的专业领域。而多相流中又以两相流最为常见,如气/液两相流,气/固两相流,油/水两相流等,其中,油水两相流广泛存在于石油开采、管道输送等工业过程中[1-2],属液液两相流范畴,在国内其研究进展远远落后于气液两相流、气固两相流及液固两相流[3]。
电容层析成像(electrical capacitance tomography,ECT)技术通过测量随流过极板间流体组分含率变化而变化的极板间电容值来重构流型图。当流过极板间流体组分含率变化时,混合流体的等价相对介电常数会随之发生变化,从而导致极板间的电容值发生相应的改变,便可将两相流中分相含率的信息以电容值的变化表现出来[4]。
图像重建算法是ECT的关键,直接关系到成像精度和成像速度。由ECT灵敏度理论可知,介质分布的微小变化对敏感场分布的影响可忽略,于是,介质分布与测得电容值之间可用简易的线性映射关系表示[5]。根据电磁场理论,由微小介质扰动方法可推导出灵敏度系数矩阵的场域表达式,从而计算灵敏度系数矩阵,即ECT正问题的求解。而ECT逆问题的求解是根据灵敏度系数矩阵计算介质分布向量,从而进行图像重构。但由于灵敏度系数矩阵往往非可逆矩阵,因此,ECT图像重构算法需要逼近灵敏度系数矩阵的广义逆,或利用迭代算法计算出介质分布向量的近似解。
压缩感知理论(compressed sensing, CS)由Donoho于2006年基于稀疏分解及逼近论[6]提出,其主要内容可表述为:若一个信号是可压缩的或在某个变换域内稀疏,则可用一个与变换矩阵非相干的测量矩阵将高维信号线性投影为低维观测向量,然后,通过求解一个稀疏最优化问题,便能够从低维观测向量中精确地重构出原始信号[7]。压缩感知理论的提出,一定条件下突破了采样定律,在远小于Nyquist采样频率的条件下用随机采样获取的离散样本,通过非线性重建算法便可恢复出原信号。目前,CS理论的研究已涉及军事、医疗、工业、社会生活等诸多领域[8]。
目前,多相流含水率在线测量研究较多的是密度法、射线法、电导率法、电容法以及电磁波法[9],几种测量方法都有一定的适用范围和使用条件。相比于其他方法,基于介电常数原理的电容法由于其结构简单,非侵入,成本低,测量精度高等优点在含水率检测中被广泛采用。
本文将CS理论运用到ECT图像重构问题中,将低维观测向量转换为低维稀疏向量,通过求解稀疏最优化问题,较为精确地重构出原信号,从而解决ECT系统的欠定性问题。利用最优阈值算法对重构图像进行灰度处理,由灰度图像对分相含率进行计算。
1 压缩感知基本理论
1.1 信号的稀疏化处理
如果N维信号x∈R最多只有k个分量不为零,即‖x‖0≤k,则该信号是k稀疏的;或者存在一个稀疏域Ψ,x可经其转换,得到一个稀疏信号,即x=Ψz,其中,‖z‖0≤k[10]。设{Ψ1,Ψ2,…,ΨN}为RN的一组正交基向量,则RN空间中的任何一个N×1的离散信号x都可以线性地表示为
(1)
其中,Ψ={Ψ1,Ψ2,…,ΨN}为N×N的稀疏基矩阵,z为x在Ψ域中的N×1维稀疏化表示向量;若z中只有少部分元素取值很大,大部分取值很小,那么可以丢弃取值较小的元素,只需要少量取值大的元素就可以较好地逼近信号x,此时,称x在Ψ域中是可压缩的。
1.2 信号的压缩采样
假设Φ为Μ×N维(Μ≪N)的观测矩阵,则使用Φ对Μ×1的高维信号x进行采样,可以得
y=Φx=ΦΨz。
(2)
其中,y为M×1的低维观测向量。令A=ΦΨ作为传感矩阵,则式(2)可写为
y=Αz。
(3)
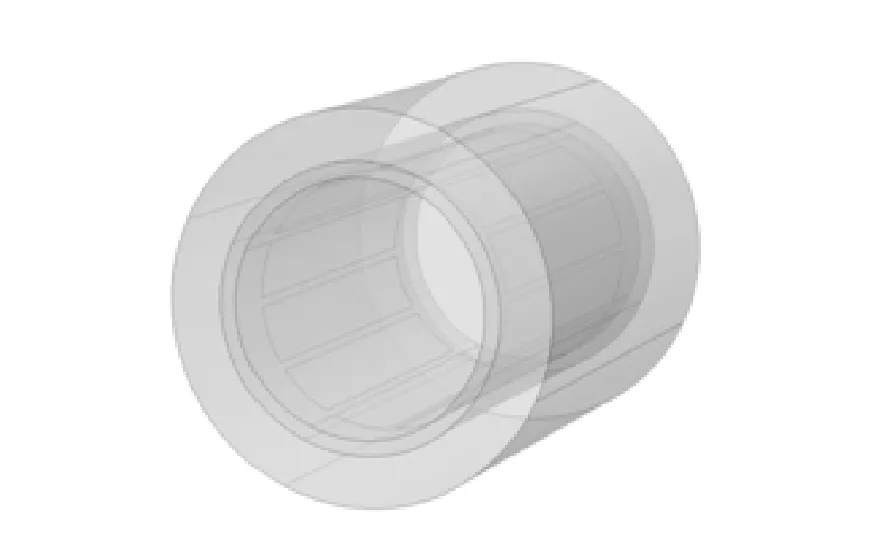
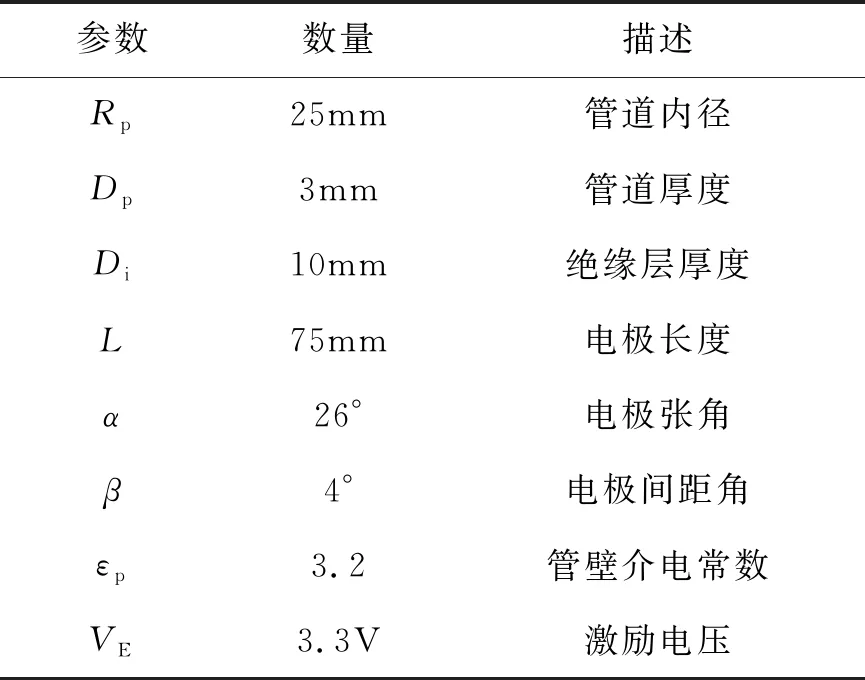
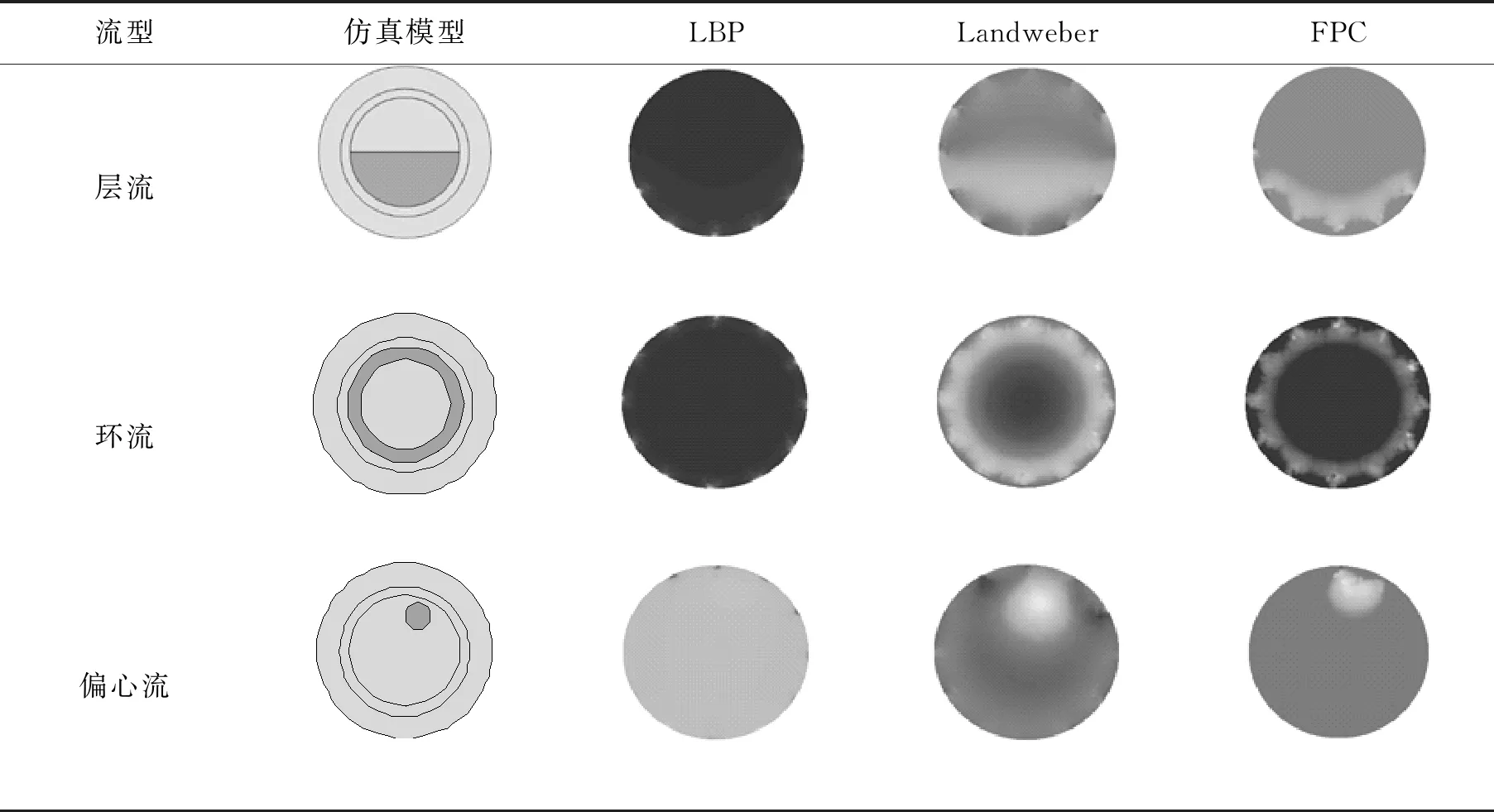
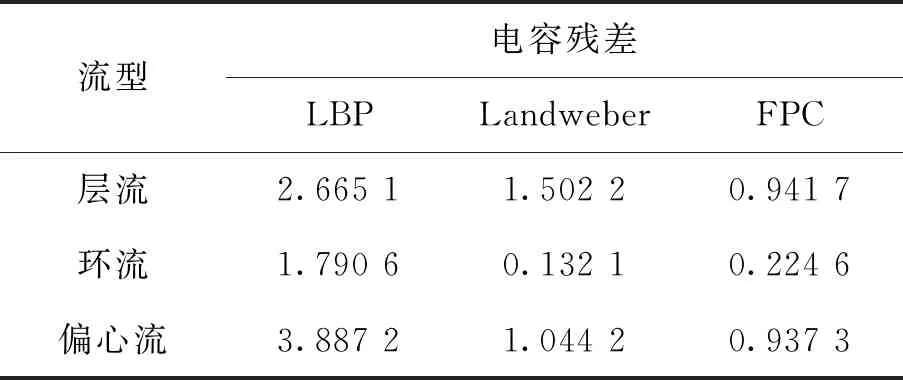
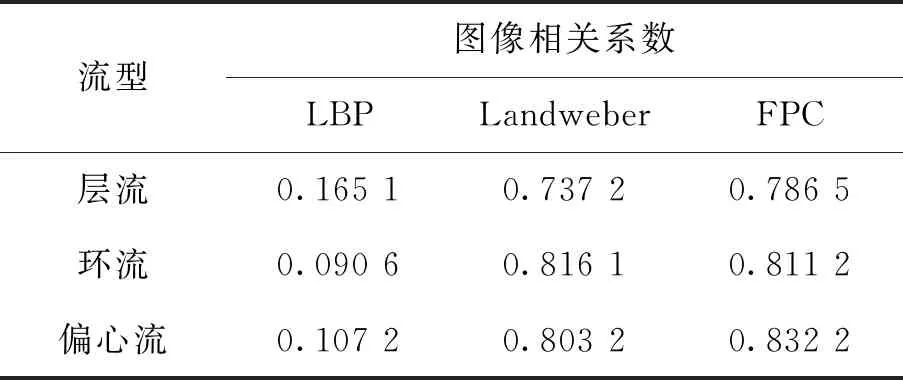
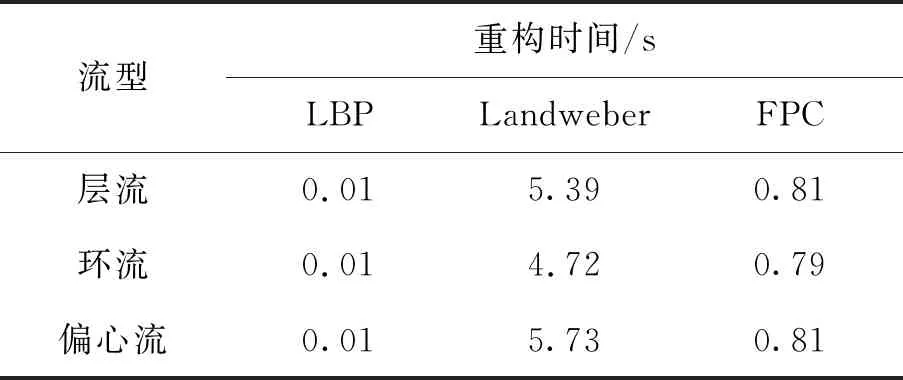
高维信号的求解过程就是由M×1维观测向量y先从式(3)中求出N×1维的稀疏向量z,再根据式(1)线性求解N×1维原始信号x的过程。当Μ Candes指出,当观测矩阵Φ与稀疏基Ψ不相关,传感矩阵Α满足等距约束条件[11](restricted isometry property, RIP),从而可求解欠定方程式(3)。 传感矩阵Α的等距约束条件可表示为 (4) 其中,δk为使得上式成立的最小值,称为传感矩阵的等距约束常数。 文献[12]证明,选择高斯随机矩阵作为观测矩阵Φ可以满足其与稀疏基Ψ的不相关性,从而使传感矩阵Α满足RIP。 最优化问题求解是压缩感知理论的最后一个阶段。当x在Ψ域中k稀疏,且当传感矩阵Α的2k阶等距约束常数δ2k<1时,式y=Αz可转化为L0范数约束最优化求解问题: (5) 由式(5)求解出稀疏向量z的唯一精确解是最直接的方法,但由于L0范数具有高度非凸性,为NP-hard问题[13]。这样的问题需要组合搜索,无法求出数值解。因而,需要寻求其他的替代模型及其相应的重建算法来求解出唯一精确的稀疏系数向量z。 松弛方法是基于L1范数最小化的思想。当传感矩阵A满足RIP条件,求解凸松弛的L1范数最小化与求解非凸的L0范数最小化问题是等价的[14],从而把式(5)转化为L1范数约束最优化求解问题,即 (6) 对于凸优化问题的求解算法目前常用的有内点法、梯度投影算法(gradient projectionfor sparse reconstruction, GPSR)以及不动点连续算法(fixed point continuation,FPC)。FPC作为一种新的基于算子分裂和连续的迭代算法,计算复杂度低、收敛速度快,能够解决大规模问题[15]。因此,本文选用FPC算法进行凸优化问题的求解。 不动点连续算法主要解决L1范数问题。通过引入正则化参数μ将式(6)约束化,得到去约束凸优化问题: (7) H(z)=g(z)+μf(z)= (8) 则根据凸优化理论[16],H(z)的最小值等价于求T(z)=∂H(z)/∂z=0。根据算子分裂理论,若H(z)可被分裂成两个凸函数相加的形式,即H=H1+H2,则有T=T1+T2。根据不动点定理, 0∈T⟺0∈(z+τT1z)-(z-τT2z), (9) 推导得 z=(I+τT1(z))-1(I-τT2(z))z, (10) 由此得到稀疏向量的迭代公式为 zn+1=(I+τT1(zn))-1(I-τT2(zn))zn。 (11) 其中,T1(z)=g(z),T2(z)=μf(z),I为恒等映射。对式(11)中的微分进行求解得 (12) 以及 (13) 根据凸优化理论,当且仅当 z=sgn(z-τf(z))⊙ (14) 为式(7)的最优解。因此,由FPC算法求解L1范数最优化问题的迭代公式可简化为 zn+1=sgn(zn-τf(zn))⊙ (15) 其中,τ,μ均为常数。 将压缩感知理论运用于电容层析成像系统时,图像的灰度向量g便是需要重构的原始信号。为了能满足CS的使用条件,需要寻找一组合适的正交基向量对需要重建的灰度向量进行稀疏化处理。目前,常用的稀疏基主要包括离散傅里叶变换基(DFT)、离散正弦变换基(DST)、离散余弦变换基(DCT)、离散小波变换基(DWT)等。文献[17]指出,DFT基可以较好地稀疏化ECT中多种典型流型的灰度向量。而经比较分析,时域基能更好地对观测矩阵进行稀疏化。因此,本文选取时域基作为稀疏基矩阵,可得 g=ΨTz, (16) ECT系统的线性模型为 c=Sg, (17) 将式(16)代入式(17)得到 c=Sg=SΨTz。 (18) 其中:c为ECT系统中的M×1维电容测量值,作为观测投影向量;S为M×N维灵敏度矩阵,作为压缩采样中的观测矩阵。 (19) 基于CS的ECT图像重构问题是典型的最小L0范数问题,可由1.3节所述的最优化问题求解算法FPC进行求解。 重构的图像向量gopt的元素大小范围为[0,1],对其进行二值化处理,可使重构图像更加清晰。本文采用最优阈值算法,搜寻阈值后,利用重构图像计算出新的电容值,并与测量电容进行比较,不断逼近以至电容误差最小。 为比较基于CS的ECT图像重构效果,本文分别选用线性反投影算法(linear back projection, LBP)、经典迭代算法Landweber以及压缩感知背景下的不动点连续算法(fixed point continuation,FPC)进行图像重构。利用COMSOL有限元计算仿真软件建立ECT传感器模型,如图1所示。最外层为接地屏蔽层;中间是PVC塑料管道,12块电极片位于管道外周;最内层是待求的成像区域。ECT传感器的几何参数如表1所示。 图1 ECT传感器仿真模型Fig.1 ECT sensor simulation model 参数 数量 描述 Rp25mm管道内径Dp3mm管道厚度Di10mm绝缘层厚度L75mm电极长度α26°电极张角β4°电极间距角εp3.2管壁介电常数VE3.3V激励电压 分别利用线性反投影算法(LBP)、经典迭代算法Landweber以及压缩感知背景下的不动点连续算法(FPC)对分层流、环状流、偏心流3种典型流型进行图像重构,结果如表2所示。 为了评价重建图像的效果,采用相对电容残差、图像相关系数、重构时间作为评价指标[19]。分别计算3种算法的重建图像评价指标,结果如表3~5所示。 表2 3种不同算法重构图像结果Tab.2 Results of reconstruct image using three different algorithms 表3 3种重构图像的相对电容残差 Tab.3 Relative capacitance residuals of reconstructed images under three algorithms 流型电容残差LBPLandweberFPC 层流2.665 11.502 20.941 7环流1.790 60.132 10.224 6偏心流3.887 21.044 20.937 3 表4 3种重构图像的图像相关系数 Tab.4 Image correlation coefficient of reconstructed images under three algorithms 流型图像相关系数LBPLandweberFPC 层流0.165 10.737 20.786 5环流0.090 60.816 10.811 2偏心流0.107 20.803 20.832 2 表5 3种重构图像的重构时间 Tab.5 Reconstructing time of reconstructed images under three algorithms 流型重构时间/sLBPLandweberFPC 层流0.015.390.81 环流0.014.720.79偏心流0.015.730.81 由重构图像及上述评价指标可看出LBP算法的重构图像基本无法用肉眼识别,辨识度很差;采用Landweber算法重构的图像边缘较为模糊,辨识度较好;而基于FPC算法的重构图像具有更清晰的边缘信息,重建图像伪迹较少,辨识度更高,更接近真实分布。此外,FPC算法的重构时间远远低于Landweber算法,满足工业成像对实时性的要求。 为进一步提升图像的重构质量,采用最优阈值算法对Landweber及FPC算法重构的图像进行图像灰度变换。处理后的效果及图像相关系数如表6所示。 表6 两种算法的灰度处理图像与相关系数 Tab.6 Grayscale processing image and correlation coefficient of two algorithms 流型Landweber FPC 灰度处理相关系数灰度处理相关系数层流0.79210.8354环流0.83320.8043偏心流0.76540.9133 从灰度图像可以看出,经最优阈值算法灰度处理后的图像效果有所改善,且FPC算法重构图像优于Landweber算法。 本文中的分相含率测量以二相流截面含水率为例,用管道截面处待定相的面积与管道截面积之比表示。油/水两相流中截面含水率的计算公式为 (20) 其中,Aw表示水的截面区域面积,Ao表示油的截面区域面积。则通过重构图像计算截面含水率的公式可表示[20-21]为 (21) fi是经最优阈值算法灰度处理后管道截面的像素值,其中,待定相的像素值为1,其余区域像素值为0;M是管道截面总的像素个数。 为了分析基于CS的ECT重构图像对于不同分相含率流体的计算能力,分别选用含有8mm,5mm,2mm三种不同内径的待定相流型进行仿真,仿真结果如表7所示。 表7 3种不同分相含率的图像重构 Tab.7 Image reconstruction of three different phase separation ratios 预设物场FPC灰度处理 预设物场的实际分相含率分别设定为10.24%,4%,0.64%;通过灰度处理后的重构图像计算得到3种分相含率的大小分别是:9.91%,3.61%,1.9%;相对误差分别是:3.22%,9.75%,70.31%。由表7中重构图像和分相含率计算结果可以看出,随着分相含率的减小,重构图像边界开始模糊,物场变形较为严重,这极大影响灰度处理中最优阈值算法求解的二值化阈值,从而导致分相含率的相对误差随着真实含率的减小而增大。 1)研究了CS理论在ECT问题中的应用,提出了稀疏基的选择方案,设计了观测矩阵;并将不动点迭代算法FPC应用于凸优化问题的求解,得出基于FPC的迭代算法。 2)建立了ECT传感器模型,并分别对3种典型两相流流型进行仿真重构,仿真实验说明,基于CS的ECT重构算法在只有少量测量数据的情况下也能精确地重建图像,解决了ECT的欠定性问题,其成像速度大幅提升,且成像质量远高于LBP,并优于Landweber迭代算法。 3)为了分析基于CS的ECT重构图像对于不同分相含率流体的计算能力,以二相流截面含水率为例,分别选用了3种不同内径的待定相流进行仿真计算,利用最优阈值算法对两种算法下的重构图像进行灰度处理。最终得出,分相含率的相对误差随着真实含率的减小而增大。因此,最优阈值算法的优化是下一步工作重点。1.3 最优化问题求解
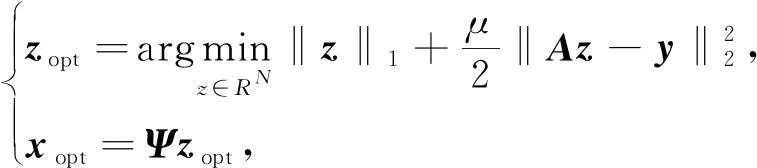
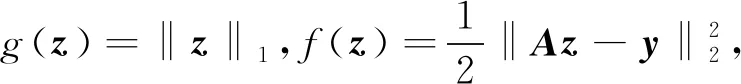
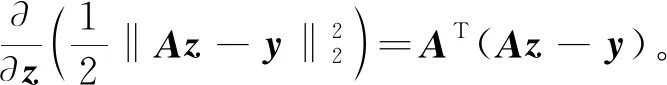
2 基于CS的ECT图像重构
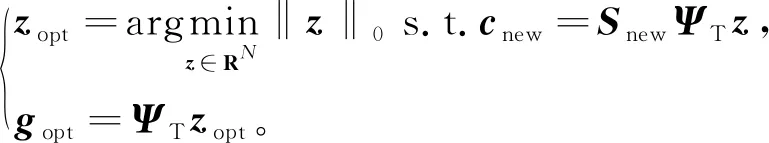
3 仿真及结果分析

4 截面含水率测量

5 结 论

