周边固支功能梯度圆板的强迫振动分析
刘小飞 龙偲 湘潭大学 湖南湘潭 411105 段启园 中北大学 山西太原 030051
功能梯度材料是多种物质复合而成的复合材料,近年来材料科学的发展有从单一物质材料发展到多种物质复合而成的趋势,从均质材料向复合材料发展,而功能梯度材料是复合材料研究的一个重要方向,近三十年才提出,材料学家和力学家以及对功能梯度材料感兴趣的科研人员与工程师进行广泛的研究和精细化的制备。
由于材料组成与性质在横向的非均匀性分布导致了功能梯度结构的应变在横向分布的复杂性,表现出与均匀材料结构不同的宏观特征。从而使得 FGM 结构的弯曲,屈曲和振动与断裂等宏观力学行为的分析要比相应的均质材料结构复杂得多。
本文研究功能梯度材料圆板的力学行为,功能梯度材料与均质板的区别是组成与性质随坐标变化,研究了功能梯度圆板随着梯度因子的变化,它的固有频率随材料参数的变化关系,以及研究了功能梯度圆板受一简谐力激励下,材料参数功能梯度因子的变化引起强迫振动的振幅与频率的影响,此研究可以帮助制备出力学性能良好的功能梯度材料。
1 功能梯度材料简介
材料作为国民科学技术的支柱之一,材料的进步标志着人类文明的进步,科技技术的快速发展使人们对材料的要求越来越高,特别在航空航天等高技术领域,航空航天发动机对材料有苛刻的要求,不仅需要有金属材料的强度和韧性,还需要有陶瓷的高熔点和高硬度,但是简单的层合组成复合材料,在高温和大温度梯度下由于热膨胀将引起剥落或龟裂,为解决此类由热应力产生材料失效的问题,日本科学家在20世纪80年代后期到90年代初提出了功能梯度材料(Functionally Graded Material,简称FGM)的概念,功能梯度材料的概念一经提出快速引起了材料界和力学界的高度注重,迅速成为了材料领域和力学领域的研究热点。
2 功能梯度圆板的自由振动分析与MATLAB求解
2.1 复合材料圆板的基本假设
本文采用的是薄型圆板,厚径比的范围是(小于1/8到1/5),功能梯度板也可以近似使用基尔霍夫薄板假设。首先圆形薄板作为弹性体,服从连续介质模型的假设,圆板材料是连续分布的,组成物质的质点之间是不存在任何间隙的,我们可以假设认为应力(σ,τ),应变(ε,γ)和位移(u,v,w)等是连续的变量或者函数,在做数学推导时可以方便的运用连续和极限的操作。
但是弹性体的均匀性假设在此不成立,材料是功能梯度材料,材料的组成结构是呈梯度变化的。
2.2 参数对自然频率的影响
(1) 参数E0对自然频率的影响
参数半径a对自然频率的影响
泊松比v 对自然频率的影响

令α=1,半径a=1,其他变量表达式的数为1,讨论厚度对自然频率的影响
ωn,现由MATLAB作图模拟厚度变化对自然频率的影响,厚度h取(0,0.2)符合薄板规定厚径比小于1/5。
参数幂指数αfalse的大小对自然频率的影响
ωn∝,厚度0.2,半径1,厚径比0.2,其他物理量表达式的值设为1,讨论幂指数因子α对自然频率ωn的影响。
3 简谐激励作用下的强迫振动与MATLAB计算
厚度为0.2m,半径为1m。厚径比为0.2满足薄板假设;设频率比q为0.1,设施加的外力为(N)。其中力的幅值0为100000(N);阻尼比为0.05。
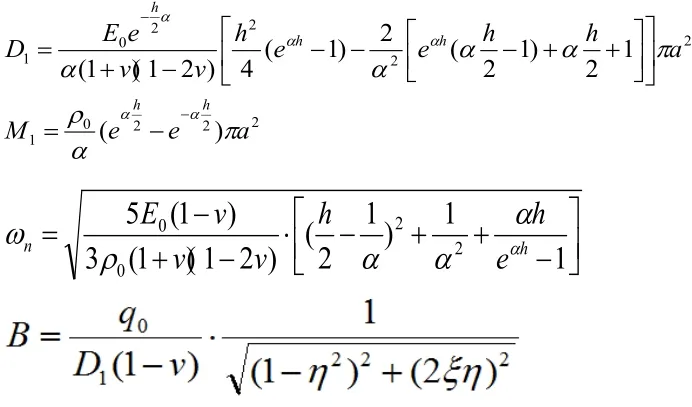
其 中3h=0.2,v =0.3,E0false=70Gpa,a=1,ρ0=2700kg/m,代入上式求出下表:

表1 不同梯度因子α对应的参数
设问题的初始条件位移为零,初速度为20m/s,固有频率不同,阻尼λ和A 值也不同;
λ为:1.0e+03*(1.1157 0.6281 0.4858 0.4218 0.3853);
A 为: 0.0008 0.0016 0.0020 0.0024 0.0026。
φ1=0将上面的参数代入下面的方程
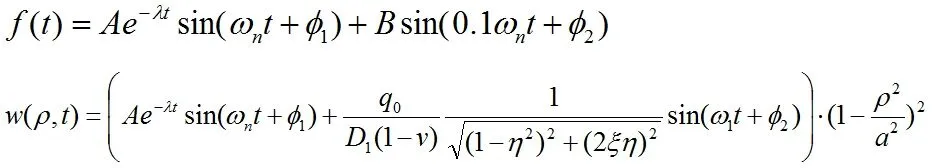
利用MATLAB绘图如下:

图3 .1梯度因子α为0.5,振幅随时间的变化关系

图3 .6 梯度因子α为0.5轴对称横向位移随时间的变化关系
随着梯度因子的增大,暂态解振幅越来越大,暂态解的振幅与初速度有关,这里假设初速度为20m/s,梯度因子增大,固有频率减小,暂态解的振幅越大,稳态解的振幅基本不变,随着时间的变化,系统趋向于简谐运动,暂态解衰减到零,系统处于稳态解的振幅函数上,系统越趋近于稳态解。功能梯度板与均质板的强迫振动的区别是梯度因子不为0,在此讨论的梯度因子是一个常数,与功能梯度材料的制备有关,一但制成就不再改变,由上节可以看出,功能梯度因子从0.5变化到2.5,固有频率逐渐减小。研究了初始的0秒到0.01秒的瞬态图像,外界频率与固有频率的关系始终是0.1倍,可以看出从暂态解到瞬态解的过渡非常短暂。
结论
本文分析的是功能梯度薄圆板小变形的振动问题,基于一般连续介质假设,运用了极坐标参考系下的方程,在分析过程中由基尔霍夫假设把纵向位移用横向位移表达式,由能量法推导了系统的固有频率,讨论了功能梯度圆板的弹性模量,泊松比,密度,厚度,半径,以及功能梯度指数幂系数αfalse对固有频率的影响,讨论了功能梯度圆板的强迫振动,运用弹性微块的平衡建立运动微分方程,运用了一个满足位移边界条件的振型表达式,表示横向位移函数,为了使问题简化,把功能梯度圆板看做是轴对称振动的,运用伽辽金积分方法,求得振幅关于时间的常微分方程,利用高数知识求解了此微分方程,得到了振幅的表达式,讨论了各参数对振幅的影响,最后给出了横向位移关于时间与半径的表达式。本文第三章与第四章求得的固有频率有偏差,可能我用能量法讨论时,忽略了纵向运动对动能的贡献。

