考虑相关性的多元输出仿真模型验证方法
林圣琳 李伟 杨明 马萍
目前建模与仿真技术已成为人们认识和改造现实世界的重要手段.由于仿真是一种基于模型的活动,仿真模型是否可信成为用户十分关注的问题.验证是仿真模型可信度评估的重要步骤[1],包含概念模型验证和结果验证.仿真结果验证最直接而有效的方法是,在相同输入条件下度量仿真输出与参考输出数据之间的一致性程度.然而,针对复杂系统建立的仿真模型往往具有不确定性、多元异类(动、静态)输出,且各输出变量间可能存在相关性,此时,若仍采用传统仿真结果验证方法将导致验证结果不准确.因此,考虑相关性及不确定性的多元输出仿真结果验证是需要重点研究的问题.
由于仿真模型和参考系统的输入及模型参数通常含有不确定性,加之仿真模型运行和实际实验过程中引入的不确定性因素和误差,导致仿真模型和参考系统的输出为随机变量或不确定的时间序列[2].考虑不确定性的影响,静态输出结果验证方法的研究多数集中在概率框架,形成了以参数估计[3−5]、假设检验[6−7]、贝叶斯因子[8−10]、证据距离[11]、概率分布差异法[12−13]为代表的5 种解决方案.其中,Oberkampf 等针对参考数据稀疏的情况,采用插值和回归分析的方法估计参考输出的均值和标准差,并与仿真输出的相应统计量进行对比,得到置信区间形式的验证结果[5];同时,假设检验和贝叶斯因子方法在静态仿真输出结果验证中的应用日趋完善,Jiang 等将贝叶斯区间假设检验应用于模型的分等级评估中[14];考虑到固有和认知不确定性的影响,文献[11]采用证据理论对动静态输出进行描述,并引入证据距离度量仿真和参考输出的一致性;Ferson等提出了概率分布差异与u-pooling 相结合的方法,用于处理稀疏参考数据情况下的单输出仿真结果验证问题[12],该方法以其原理简单、可操作性强等优点得到了广泛应用.
考虑不确定性的同时,复杂仿真模型可能存在多个输出变量的情况,且各变量间可能存在函数或相关关系.在单变量静态输出结果验证方法的基础上,针对多元输出仿真结果验证方法的研究取得了一定的进展.例如,Rebba 等最先提出了假设检验、贝叶斯因子与协方差相结合的多元输出结果验证方法,并引入了非正态验证数据转化为正态数据的方法以满足假设检验的条件[15];Jiang 等将区间贝叶斯因子方法进行推广,将其应用至多元静态输出结果验证问题中[16];Zhan 等提出了基于概率主成分分析(Probabilistic principal component analysis,PPCA)与贝叶斯因子相结合的方法,用于解决带有不确定性和相关性的多元动态输出结果验证问题[17].同时,Li 等将概率积分变换(Probability integral transformation,PIT)与概率分布差异法相结合,将多变量累积概率分布转化为单变量概率分布的形式,采用概率分布差异法计算仿真和参考输出累积概率分布的差异[18];Zhao 等分别计算仿真和参考输出与相应总体分布的马氏距离,进而得到仿真和参考输出马氏距离的累积概率分布,并应用概率分布差异法计算两者的差异[19].
从单变量验证到多变量验证,各变量间的关系是研究的重点,现有验证方法存在验证结果不够准确和全面的问题.利用传统单变量验证(或结合多种预处理方法)对各变量进行分别验证再综合,一是对带有相关性的多个验证结果进行加权综合导致最终验证结果不够准确;二是未考虑多变量间相关性的验证将导致验证结果不全面.此外,对复杂仿真模型进行结果验证,其输出变量间的关系不够明确.此时需首先明确输出变量间的关系(独立/函数/相关关系)再进行验证,现有的多变量验证方法仅适用于变量间关系已知的情况.同时,多变量验证方法均利用协方差矩阵度量变量间的相关性,这对非线性等其他相关关系将不再适用,导致多变量间相关性度量不够准确.
为解决上述问题,提出基于变量选择和概率分布差异相结合的多元输出仿真结果验证方法,对具有不确定性的多元异类输出进行联合验证.第1 节对多元输出结果验证问题进行描述与分析,指出现有方法存在的问题;第2 节给出多元静、动态输出的相关性分析及变量选择方法;第3 节提出基于数据特征提取和联合概率分布差异的多元输出仿真结果验证方法;第4 节给出应用实例与对比实验结果;第5 节给出本文结论.
1 问题描述与分析
用S表示系统,Ss和Sr分别表示仿真模型和参考系统,用As={as1,as2,···,asp}和Ar={ar1,ar2,···,arp}分别表示仿真模型和参考系统的输入变量集,p为输入变量个数,Ys={ys1,ys2,···,ysm}和Yr={yr1,yr2,···,yrm}分别表示仿真模型和参考系统的输出变量集,m为输出变量个数,多元异类输出集Ys、Yr中的静态输出表示为随机变量,动态输出表示为多个时间序列集合的形式.假设ysi、ysj分别为仿真模型的某一动态和静态输出,则有
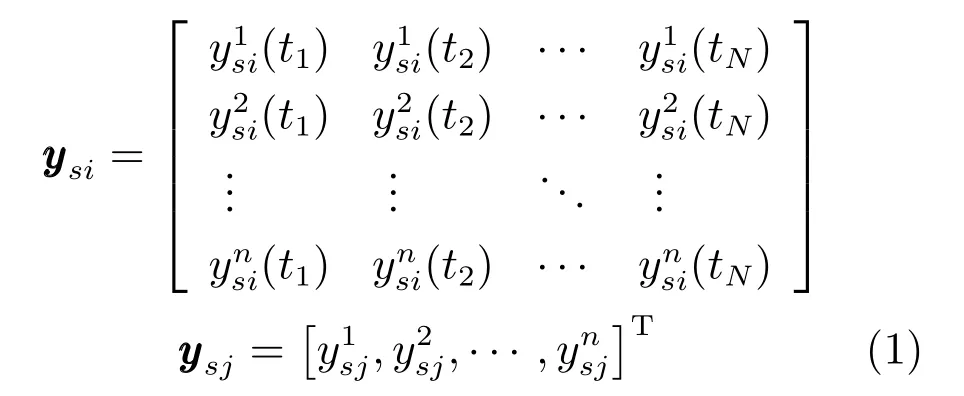
式中,i,j ∈[1,m],且=j;N为时间序列的长度;t1,t2,···,tN表示时间序列的时刻点;考虑不确定性的影响,需要进行多次仿真和实际实验,n为重复实验次数.用C(Ys,Yr)表示在As=Ar时,Ys相对于Yr的一致性程度,且C(Ys,Yr)∈(0,1].当Ys与Yr完全一致,则有C(Ys,Yr)=1;当Ys相对于Yr的一致性程度越差,表示仿真模型越不可信,则有C(Ys,Yr)→0[1].
假设YsJ ∈Rns×m与YrJ ∈Rnr×m为多元仿真模型和参考系统的静态输出变量,ns、nr表示仿真和实际实验的重复运行次数.针对带有相关性的多元静态输出结果验证方法主要有:
1)基于假设检验和马氏距离相结合的方法.文献[16]给出基于似然比检验和马氏距离相结合的验证方法,得到最终一致性结果.
2)基于主成分分析的方法[17].对YsJ和YrJ进行降维,去除变量间相关性,得到新的输出变量和,η ≤m为主成分的个数,而后采用现有静态输出验证方法对若干主成分进行逐一验证并综合得到最终验证结果.
3)基于概率分布差异的方法[18].分别计算m维YsJ和YrJ的联合累积概率分布(Cumulative distribution function,CDF)函数并作差,获得仿真和参考输出数据的差异,得到[0,+∞)的误差度量结果.
针对带有相关性的多元动态输出结果验证问题,常用方法为基于数据特征和主成分分析相结合的方法[17].首先分别提取动态输出数据的特征矩阵,而后采用基于主成分分析的多元静态输出验证方法获得最终验证结果.针对上述多元输出仿真结果验证方法进行分析,存在以下问题需要进一步研究:
1)复杂仿真模型常存在多元输出变量间的相关或独立关系未知的情况,目前方法均是在变量关系已知的前提下进行研究,存在一定局限性;
2)利用主成分分析获取的多元输出变量的主成分是线性变换后的结果,被提取主成分所代表的变量含义不够明确,同时对多元输出变量进行降维将导致验证信息丢失,使验证结果不够准确和全面;
3)采用协方差矩阵度量变量相关性,需假设变量样本服从正态分布,且仅能描述多元输出变量间的线性关系,无法度量变量间非线性等其他相关关系,进而导致变量间相关性度量不准确;
4)基于联合概率分布差异法可直接度量多元静态输出变量间的差异,需要已知变量间的独立或相关关系,同时,处理多元动态输出存在局限,得到的差异度量结果无法刻画仿真模型的可信度.
为解决上述问题,可采用基于变量选择和概率分布差异相结合的多元输出仿真结果验证方法,考虑不确定性的影响,对选取到具有相关性的多变量进行联合验证.首先,引入变量选择方法分别对Ys、Yr进行相关性分析,提取相关变量子集(又称相关变量组,子集中各变量是相关的,各子集中变量数的和为输出变量总数),进而得到多个独立的变量子集;同时,提取相同变量子集中多变量的数据特征,对于静态输出选取数据本身作为变量特征,对于动态输出选取距离、形状以及频谱特征;而后计算变量子集中多个变量关于某特征的联合CDF 差异,并将其转化为可信度;最后将多个变量子集关于若干数据特征的一致性与多个动态输出均值曲线的一致性进行综合得到仿真模型可信度.
2 多元输出相关变量选择方法
为明确复杂仿真模型中多元输出变量间的独立或相关关系,引入数据挖掘领域的相应方法对多变量进行相关性分析,进而提取相关变量子集.本文仅考虑同种类型(静态或动态)输出变量间的相关性,利用分形维数和互信息方法分别对静、动态输出变量进行相关性分析.
2.1 基于分形维数的静态相关变量选择方法
对随机变量的相关性分析集中于Pearson 相关系数,它仅能度量变量的线性关系,并对变量间强相关性较敏感,其结果受奇异值的影响较大,无法适应具有非线性、不确定性以及非正态分布的数据集.其他一些相关系数,如Kendall 系数、Spearman系数等虽可以描述非线性相关关系,但却不能完整地刻画变量间的相关性结构.此外,数据挖掘领域常用的变量选择方法,如奇异值分解法(Singular value decomposition,SVD)、主成分分析法(Principal component analysis,PCA)、基于神经网络的方法(Neural networks,NN)、基于k-邻近方法(K-nearest neighbor,KNN)、基于决策树的方法(Decision tree,DT)、基于贝叶斯网络的方法(Bayesian network,BN)以及基于分形维数的方法(Fractal dimension,FD)等,具有不同的特点,对其进行对比分析如表1 所示.
由表1 可知,SVD 和PCA 方法得到的变量子集失去了其原有的含义,且只能对具有线性相关性的变量集进行分析;而基于机器学习的方法需要训练样本集作为支撑,其运行速度受到变量个数的影响较大,导致变量个数较多时运行速度较慢;而基于分形维数的方法不仅能够度量线性相关性,还能度量非线性等其他相关关系,具有不需要训练样本集和运行速度快等优点.因此,本文引入基于分形维数[20]的方法对多元输出变量进行分析,提取相关变量子集.假设YsJ、YrJ为仿真和参考多元静态输出变量集,以为例给出YsJ的相关变量子集提取步骤如下.
步骤1.根据自相似性原理计算的局部固有维度pD(·):
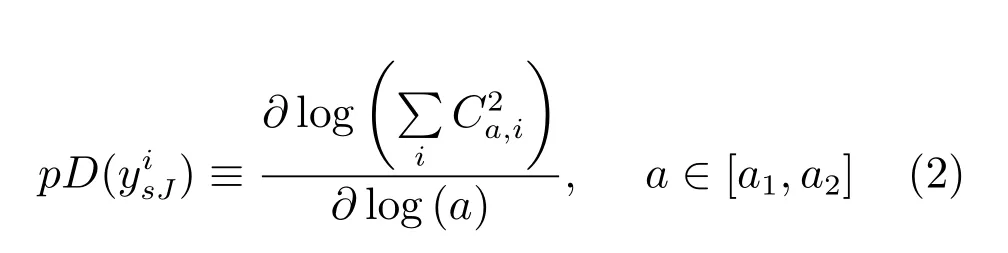

表1 常用变量选择方法对比Table 1 Comparison of general variable selection methods
式中,r表示将划分成2υ个相等大小区间的长度,υ为划分深度,表示中落入第i个区间的样本个数;
步骤2.设c=1,移除YsJ中的变量,ξ为预定义的固有维度阈值,排除的变量为独立变量,并按照pD(·)大小将进行降序排列,形成新变量集其变量个数为;
步骤3.计算直到
步骤4.若,则算法结束;
步骤5.设相关性变量超集并提取ξSGc中的相关变量子集ξGc和相关变量基ξBc,具体算法见文献[20],并设循环变量j=k+1;
步骤6.若,则执行下一步,否则转至步骤8;
步 骤 7.对于ξBc中的每个变量,若同时成立,则将加入ξGc;
步骤8.执行j ←j+1,若,则转至下一步,否则转至步骤6;
步骤9.移除中ξGc −ξBc的变量,并输出相关变量子集ξGc和相关变量基ξBc;
步骤10.执行c ←c+1,并转至步骤3.
通过上述步骤提取YsJ和YrJ的相关变量子集如下.
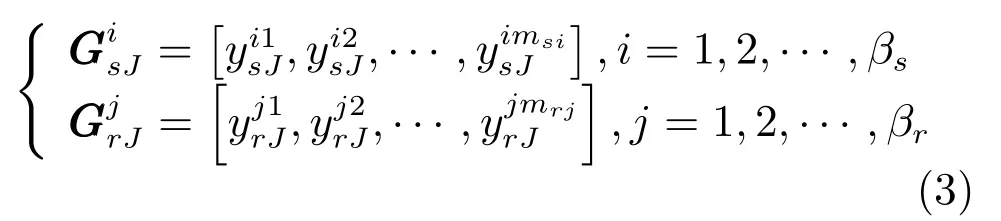
式中,βs、βr分别为提取YsJ和YrJ相关变量子集的个数,msi、mrj分别为中变量的个数,且有ms1+ms2+···+msi=mr1+mr2+···+mrj=m.
2.2 基于互信息的动态相关变量选择方法
与随机变量不同,多元动态输出变量与时间有关,其相关性分析与变量选择需从时间序列整体的角度进行分析.一些传统的随机变量相关性分析方法对于多元动态变量同样适用,例如Pearson 系数、Kendall 系数、Spearman 系数等,但无法用于动态输出变量具有多个样本(时间序列)的情况.此外,一些统计学分析方法,如Granger 因果关系分析[21]、典型相关分析[22]、Copula 分析[23]、灰色关联分析[24]以及互信息分析[25]等同样能够用于多变量的相关性分析.Granger 因果关系分析只能定性地分析变量间的因果关系,而无法得到定量的结果;典型相关分析对观测值的顺序不会做出响应,因此无法解决时间序列问题;Copula 分析需要建立在对边缘分布的合理假设之上,使其应用受到限制;灰色关联分析仅从形状相关性的角度对时间序列进行分析,其相关性度量不够全面.
基于互信息的相关性分析方法能够度量动态输出变量间任意类型的关系,互信息以信息熵为理论基础,它能够度量变量取值的不确定性程度,进而描述变量的信息含量大小[26],通常用于多种类型时间序列的特征提取和结构化预测[27].然而,互信息同样存在不能完整刻画变量集相关性结构的缺点,因此本文引入类可分性和变量可分性提取多元动态输出的相关变量子集[28].假设YsD、YrD为仿真和参考多元动态输出变量集,同样以YsD为例,给出变量选择步骤如下.
步骤1.计算YsD的m×m维互信息矩阵,具体算法见文献[26];
步骤2.分别计算每一维变量的类间离散度Ωbi和类内离散度Ωwi:
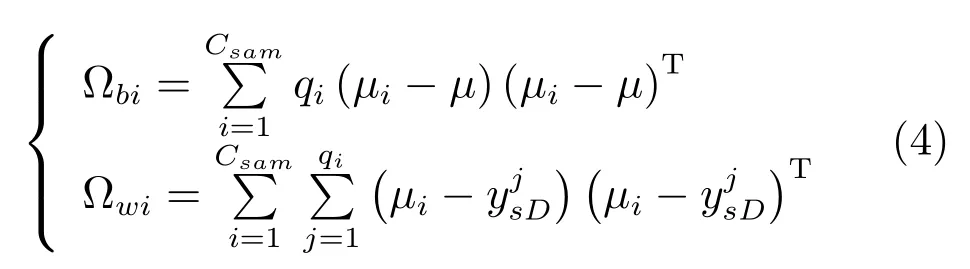
式中,Csam为样本类别总数,qi为属于第i类的样本个数,按照每个变量的类可分离性大小,进行变量排序:
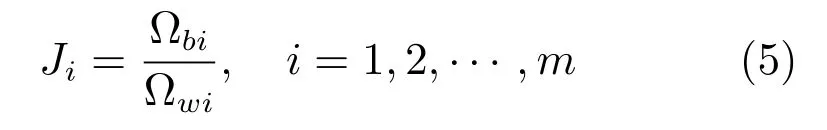
步骤3.取Ji值最大的变量为变量子集的第一个变量;
步骤4.选择使下式最大的变量为的下一个变量:
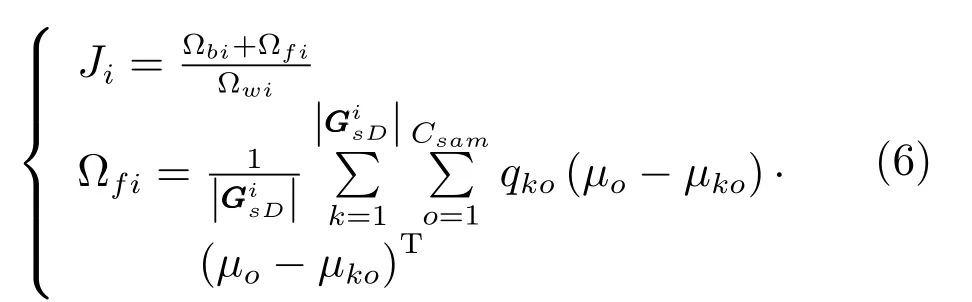
步骤5.当则算法终止,其中,ε为预设值,否则转至步骤4.通过上述步骤得到相关变量子集如下:

式中,i=1,2,···,βs,j=1,2,···,βr.βs、βr的含义与式(3)相同.
3 多元输出仿真结果验证方法
考虑不确定的影响,若对每一时刻的多元动态输出变量进行分析势必导致维数爆炸.为此提出基于特征的验证方法,首先提取用户关注的输出数据特征,而后计算每个特征下多变量联合概率分布的差异,并将其转化为可信度结果,最后综合多个验证结果得到模型可信度.
3.1 多元输出数据特征提取方法
针对于静态输出,选取数据本身作为变量特征.假设Ys ∈Rns×m与Yr ∈Rnr×m为多元仿真和参考静态输出变量,其数据特征描述为

对于动态输出ysij(t)、yrik(t),i=1,2,···,m,j=1,2,···,ns,k=1,2,···,nr则选取ns、nr次系统运行得到的输出均值曲线作为基准,与每次实验得到的输出曲线进行对比,求取相应的均值曲线的第l个特征:
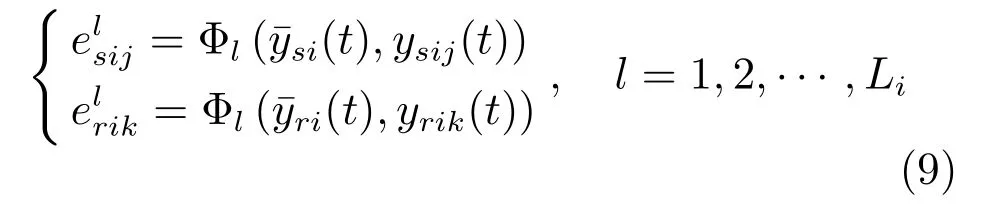
式中,Li为第i个输出的特征数,Φl(·)为第l个特征度量模型.
提取动态输出特征前,需要先对动态输出进行归类[1].以第j个动态输出的第i次实现yij(t)为例,其对应的时间变化序列为[t1,t2,···,tN].则定义yij(t)随时间变化的频率为:

式中,Fij ≥0 为yij(t)的变化频率;∆yij(tk)=yij(tk+1)−yij(tk);∆tk=tk+1−tk;给定F0为判断时间序列变化快慢的临界值,若Fij ≥F0,则认为yij(t)为速变数据,否则为缓变数据.
为刻画不确定性对系统输出的影响, 从距离和形状两方面提取缓变数据的特征. 在前期工作[29]的基础上, 给出第j个仿真输出的第i次实现ysij(t)与其均值曲线的距离和形状差异的度量公式如下.
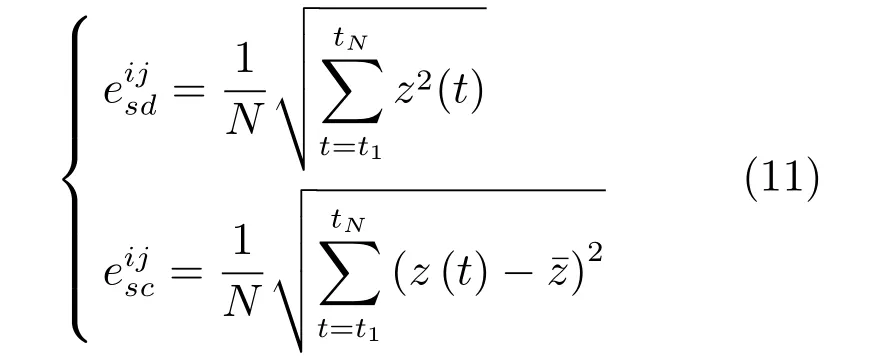
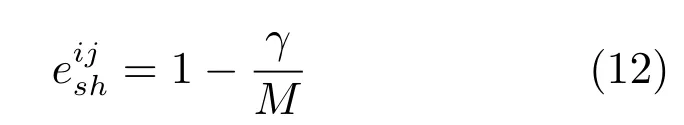
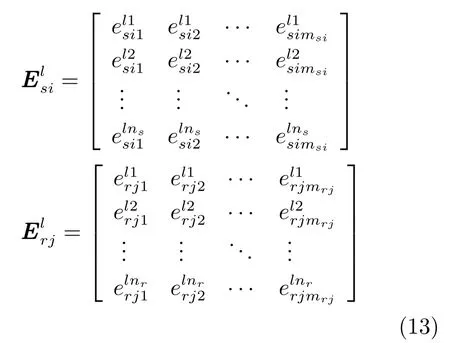
式中,i= 1,2,··· ,α,j= 1,2,··· ,β. 若Gsi和Grj均为静态输出变量子集, 则Li= 1; 若Gsi和Grj均为缓变输出变量子集, 则Li= 2; 若Gsi和Grj均为速变输出变量子集, 则Li=1. 需要说明的是, 在某些特殊仿真应用中, 除了上述特征外, 通常还需关注数据本身的一些特征, 例如控制系统阶跃响应中的上升时间、超调量以及稳态误差, 位置数据中的变化趋势, 测量数据中的噪声等. 在进行实际验证中, 特征矩阵包含两部分内容, 一部分为上文给出的数据特征, 另一部分为根据具体领域知识确定的数据特征.
3.2 基于概率分布差异的特征一致性分析方法
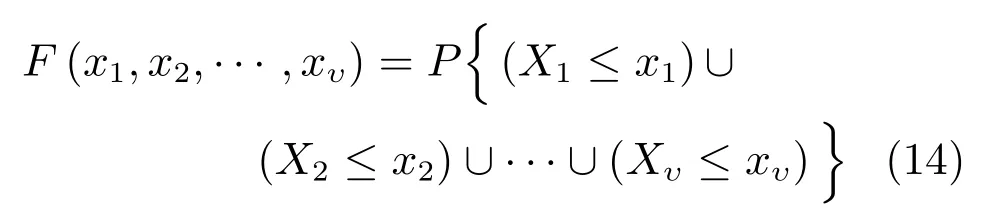
将υ维空间划分为等尺寸的ρυ个区域,遍历υ维变量的ρ个取值区间,若则F(x1,x2,···,xυ)=0;若则F(x1,x2,···,xυ)=k/ρυ等.如果变量集x1,x2,···,xυ在第k个区间内的样本量为1,则F在x1,x2,···,xυ点的跳跃度为1/ρυ,如果变量集x1,x2,···,xυ在第k个区间内有ε个样本,则F在x1,x2,···,xυ点的跳跃度是ε/ρυ.给出EEElsi和联合CDF 间的差异如下.

为计算联合CDF 的差异D(Fr,Fs),可将上式改写为下面积分之差的形式:
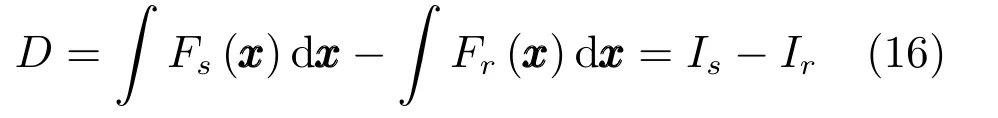
式中x=[x1,x2,···,xυ].假设分别用估计Is和Ir,并用估计,则的方差为:
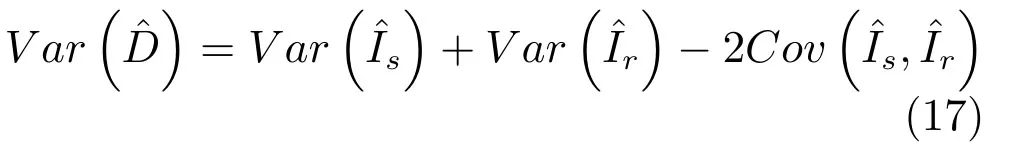
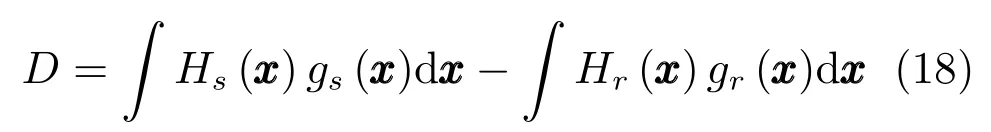
其 中,x=x1,x2,···,xυ,gs(x)、gr(x)是 两个密度函数,Hs(x)=Fs(x)/gs(x),Hr(x)=Fr(x)/gr(x).首先,由gs(x)、gr(x)各产生P个相互独立的υ维随机数Ts1,···,TsP和Tr1,···,TrP,并计算
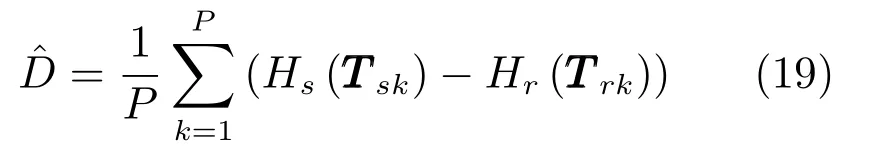
采用逆变换方法由同一个υ维联合均匀分布U(0,1)产生Ts1,···,TsP和Tr1,···,TrP,能够保证两组随机数具有较高的正相关程度,进而使较小,对的估计值趋于稳定.
需要说明的是,D(Fs,Fr)∈[0,∞)仅是仿真和参考输出特征的联合CDF 的差异(如图1 所示),其取值范围为[0,∞),此时无法给出仿真和参考输出的一致性程度(即取值为[0,1]的相对值).因此,提出将D(Fs,Fr)向可信度C(Fs,Fr)转化的公式如下.

性质1.非负性:C(Fs,Fr)≥0;
性质2.交换性:C(Fs,Fr)=C(Fr,Fs);
性质3.有界性:C(Fs,Fr)∈[0,1];
性质4.同一性:C(Fs,Fr)=1,当且仅当Fs=Fr.
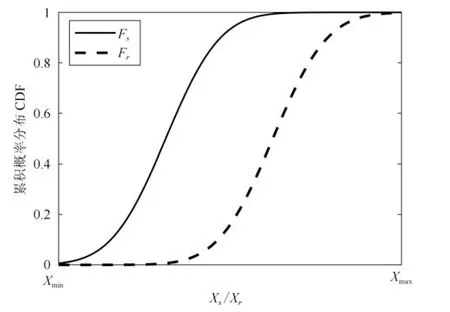
图1 参考与仿真输出的CDF 对比Fig.1 Comparing CDF curves of reference and simulation output
3.3 多元输出仿真结果验证方法流程
基于前文所述方法,给出考虑相关性的多元输出仿真结果验证流程如图2 所示.
1)考虑不确定因素的影响,分别进行n次仿真运行和实际试验,获取多元仿真和参考输出Ys={Ys1,Ys2,···,Ysm},Yr={Yr1,Yr2,···,Yrm};

图2 考虑相关性的多元输出仿真结果验证方法流程Fig.2 Procedures of multivariate simulation result validation under correlation
2)利用多元输出变量选择方法提取Ys、Yr的相关变量子集Gsi,i=1,···,βs,Grj,j=1,···,βr;
3)若βs=βr且Gsi=Grj,则依据式(8)∼(13)提取Gsi、Grj中各变量的数据特征反之,若βs=βr或的相关变量子集,则认为该仿真模型不可信,即C=0,算法结束;
5)依据式(15)∼(19)计算特征变量集的联合CDF:Fsil、Frjl的差异
7)通过2)可知,α个相关变量子集之间是相互独立的,且用户关注的多个数据特征(包括位置、形状、频谱)间也可认为是独立的,进而可采用加权方法综合多个可信度结果l=1,···,Li;i=1,···,βs;j=1,···,βr.图2 中“Integrate(·)”表示加权综合算子.同时第σ个动态输出的均值曲线可认为是对系统输出的一次抽样,不考虑不确定性影响时的多元输出数据是近似独立的,进而综合得到最终验证结果如下所示.
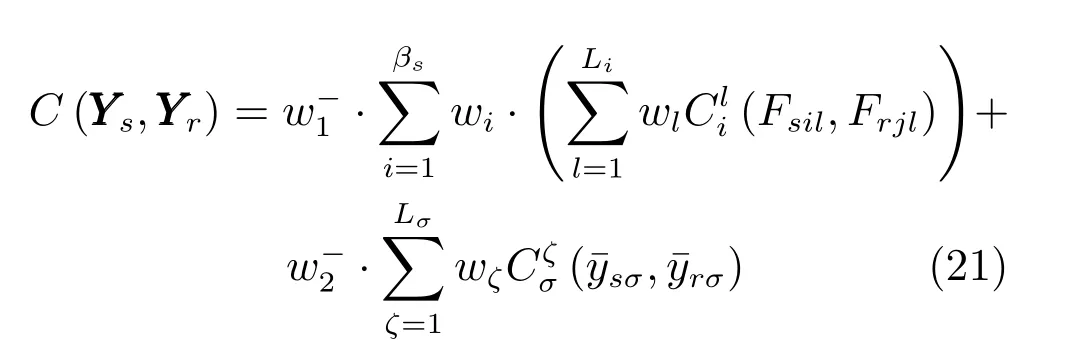
其中,σ=1,···,mdynamic表示第σ个动态输出变量,ζ=1,···,Lσ表示动态输出均值曲线的第ζ个特征,wl、wζ代表第l、ζ个数据特征的可信度结果权重,wi代表第i个相关变量子集的一致性分析结果权重,代表相关变量子集和动态输出均值曲线一致性的权重.
4 应用实例与分析
为验证本文方法的有效性,针对文献[2]中给出的某飞行器纵向平面内末制导阶段的仿真模型进行结果验证.该模型包括飞行器制导模型和目标运动模型.图3 给出纵向平面内弹目相对运动几何关系.目标以恒定速度vT沿x轴向右行驶.假设飞行器无动力飞行且航向已对准目标,忽略地球自转,给出以时间为自变量的飞行器纵向质心运动方程
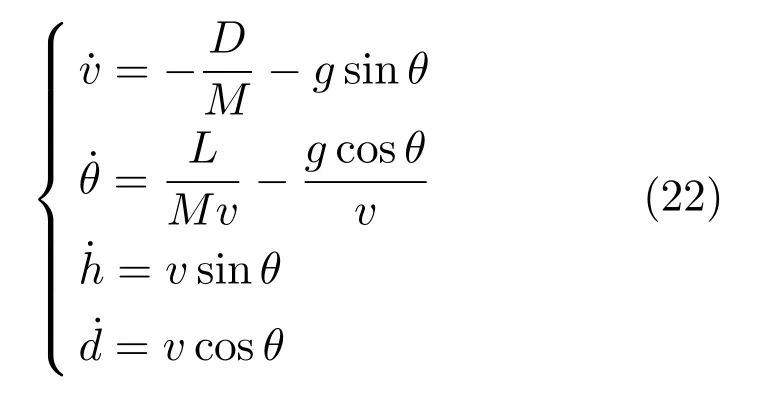
式中,v为速度,θ为弹道倾角,h为高度,d为水平距离.阻力D=0.5ρv2SCD(Ma,α),升力L=0.5ρv2SCL(Ma,α).CD与CL分别为阻力系数与升力系数.α为攻角,马赫数Ma=v/vs,S为参考面积,M为质量,αM为法向加速度,λ为视线角.声速vs与大气密度ρ根据1976 年美国标准大气计算.相应的制导律设计可见文献[30].根据上述信息建立该飞行器纵向平面内末制导仿真模型.

图3 纵向平面内弹目相对运动几何关系Fig.3 Geometrical relationship of relative missile-target movement in longitudinal plane
利用此仿真模型精确研究此飞行器在末制导阶段的特性,需要考虑其受到的不确定性因素.飞行器升力与阻力均存在不确定性,引入升力系数扰动CLC,与阻力系数扰动CDC模拟阻力系数与升力系数的不确定性,因此有升力L=0.5ρv2SCLCCL(Ma,α),阻力D=0.5ρv2SCDCCD(Ma,α),分别采用不同分布对CLC和CDC进行描述.同时,大气密度会影响升力和阻力,因每次飞行环境不同需考虑其不确定性的影响,采用大气密度系数Cρ表示.此外,飞行器进入末制导阶段时的初始视线角λ0与弹道倾角θ0亦具有不确定性.选取仿真模型和参考系统的不确定参数如表2 所示.

表2 飞行器末制导过程的不确定参数取值Table 2 Uncertainty parameters values in the terminal guidance process of flight vehicle
选取用户关注的多元输出变量如表3 所示.选取静态输出变量有飞行器的最终落点位置坐标(xf,zf)和目标终点位置坐标(xT f,zT f),同时选取待验证的动态输出变量有弹道倾角θ、攻角α、视线角λ、弹目相对距离DMT、目标速度vT.利用拉丁超立方抽样法,对模型不确定性参数进行抽样,给定初始样本数为1 000,运行仿真模型共得到1 000 组输出.改变飞行器模型参数(见表2),采用拉丁超立方抽样获得的1 000 组数据作为参考输出.系统输出数据的包络线如图4∼10 所示.其中目标速度vT、目标终点位置zT f为恒定值,未在图中标出.

表3 待验证的模型输出Table 3 Model outputs to be validated
利用本文方法对该飞行器末制导仿真输出进行验证.首先利用多元输出变量选择方法分别对仿真和参考的动静态输出变量进行相关性分析及变量选择,得到相关性分析结果如表4 所示.通过分析可知,仿真和参考输出变量具有相同的变量子集,动态输出变量θ、α、λ、DMT具有相关性,故将其归为一类.vT为定值(不随时间改变)并与变量子集I 相互独立;静态输出xf、xT f具有相关性,通过验证可知两者满足线性关系(如图11 所示),同时zf与xf相互独立(如图12 所示),进而可得zf与xf相互独立,zT f为定值0 形成了变量子集III.由上述分析结果验证了变量选择方法的有效性.
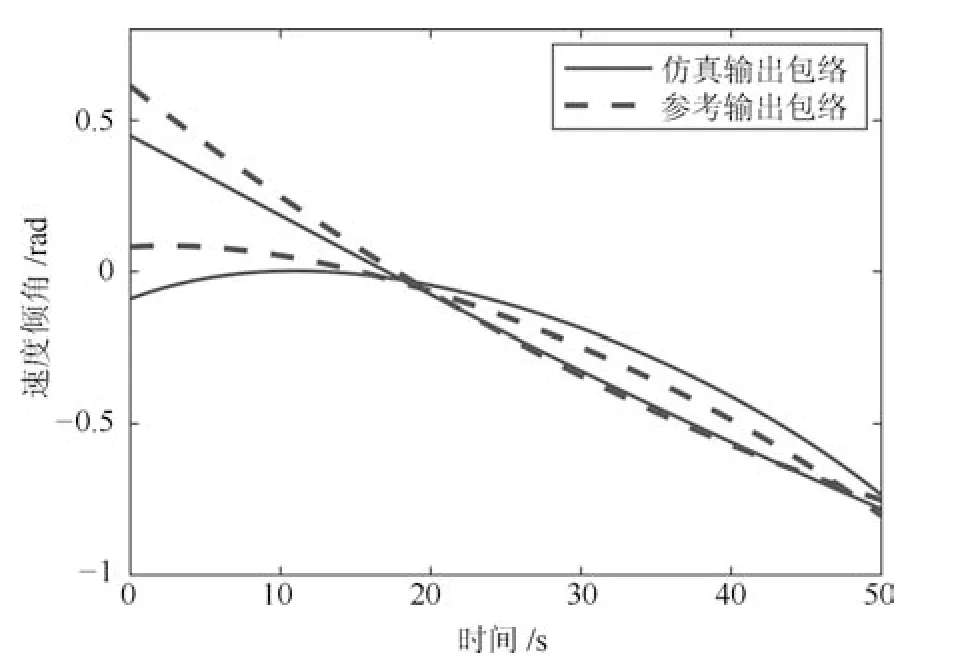
图4 弹道倾角输出包络线Fig.4 Envelope lines of launch angle
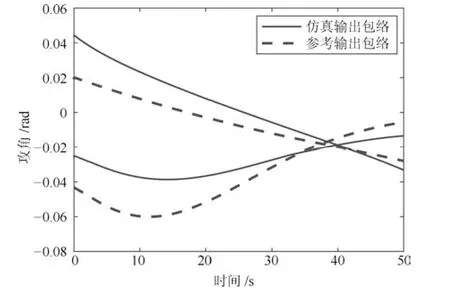
图5 攻角输出包络线Fig.5 Envelope lines of angle of attack
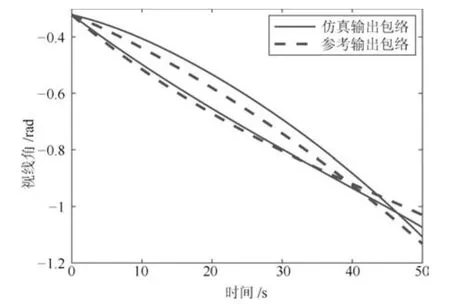
图6 视线角输出包络线Fig.6 Line-of-sight angle envelopes
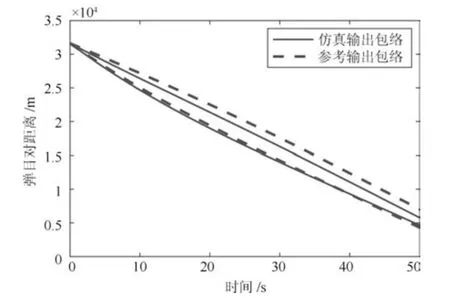
图7 弹目相对距离输出包络线Fig.7 Envelope lines of the missile-target relative distance

图8 飞行器落点X坐标输出散点图Fig.8 Scatter diagram of X-direction drop point coordinates of the flight vehicle
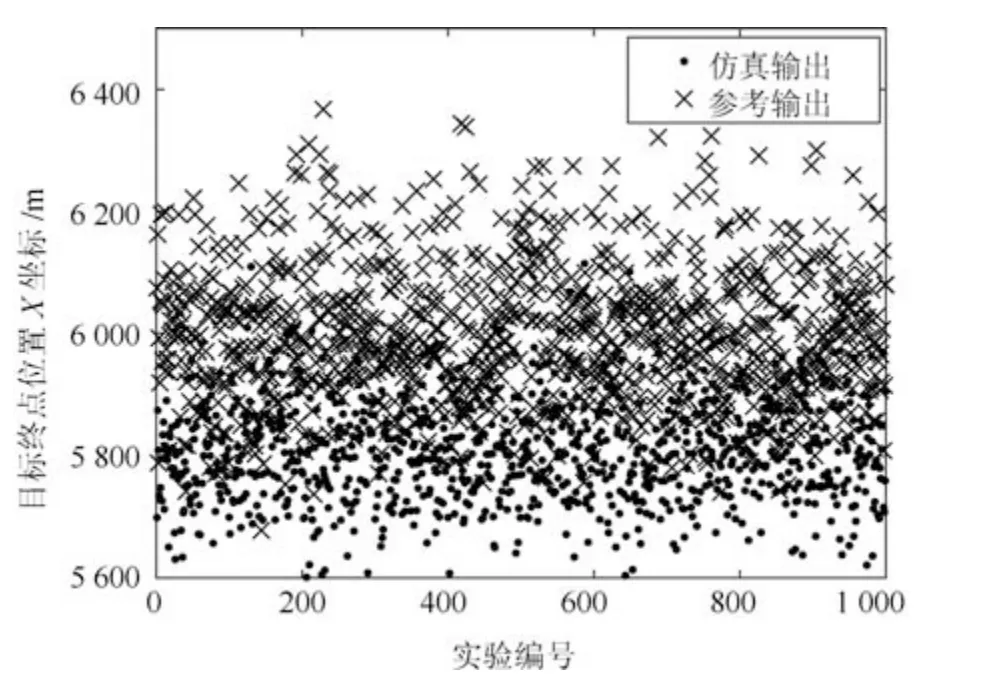
图9 目标终点位置X坐标输出散点图Fig.9 Scatter diagram of X-direction terminal point coordinates of the target vehicle
根据表4 的变量选择结果求取各变量子集关于某特征的联合CDF,选取动态输出的位置和形状特征,分别求取变量子集I 的联合CDF,变量子集II为恒定值在验证过程中直接采用相对误差方法进行一致性分析即可;对于静态输出变量子集I 关于数据本身的联合CDF 如图13 所示,变量子集II 的CDF 曲线如图14 所示.进而得到动态输出均值曲线的一致性结果(见表5)以及多个变量组关于多个特征的CDF 差异和可信度结果(见表6).依据式(21)综合多个可信度结果得到最终验证结果为0.82,由于仿真和参考输出变量vT、zT f均相等且恒为0,故在计算模型可信度时不予考虑,为方便计算采用均权的方式进行综合.
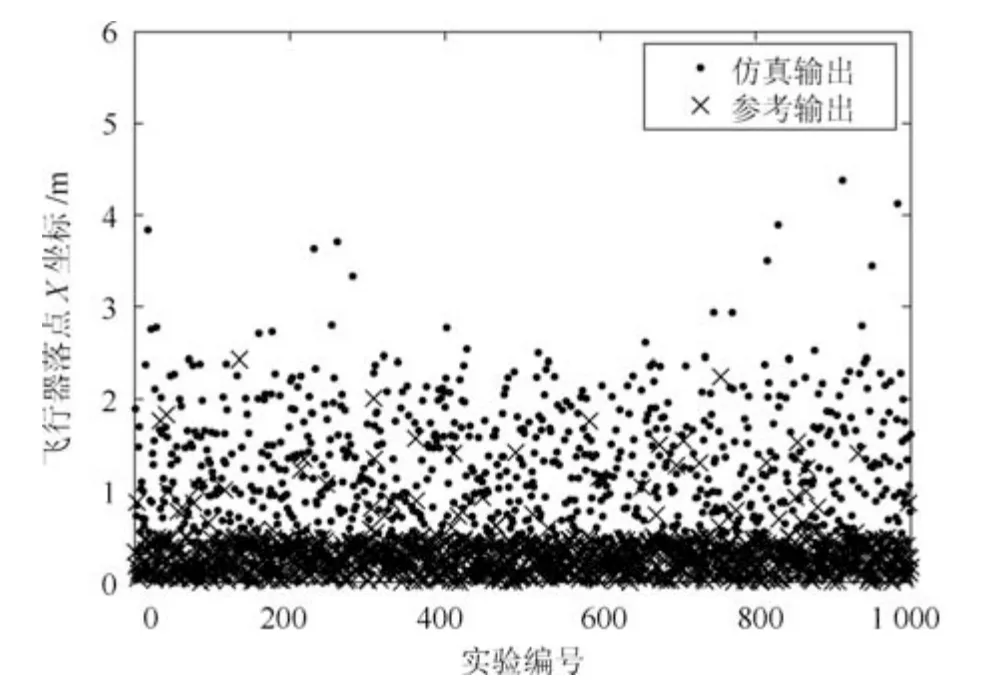
图10 飞行器落点Z坐标输出散点图Fig.10 Scatter diagram of the terminal point of the target in the Zdirection

表4 多元输出变量选择结果Table 4 Variables selection results of multiple outputs
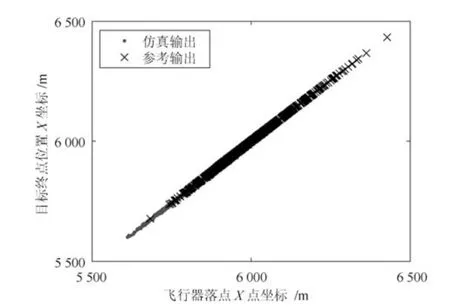
图11 飞行器落点X坐标与目标终点位置X坐标间的关系Fig.11 Relationship of X-direction coordinates between drop point of flight vehicle and terminal point of target
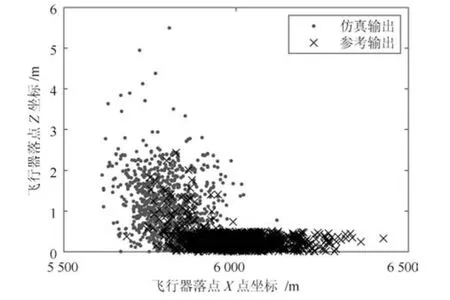
图12 飞行器落点X方向坐标与Z方向坐标间的关系Fig.12 Relationship between X-direction and Z-direction coordinates of the drop point of flight vehicle

图13 仿真和参考静态输出变量子集I 的联合CDF 对比Fig.13 JCDF comparison of variable subset I between static simulation and reference output
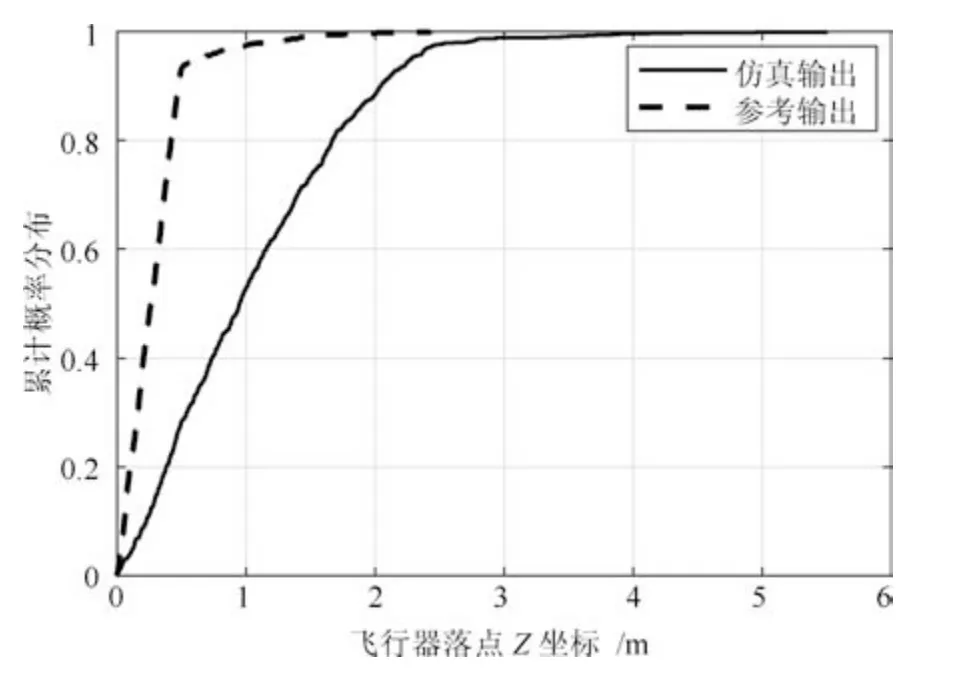
图14 仿真和参考静态输出变量子集II 的CDF 对比Fig.14 Comparison of variable subset II between static simulation and reference output
此外,为进一步验证本文方法对参数不确定性度量的有效性,针对上述应用实例分别设计两组验证实验(不确定性参数取值见表7).固定仿真模型和参考系统的不确定性参数大气密度系数Cρ、升力系数CD、阻力系数CL和初始视线角λ0的取值.分别调节仿真模型初始弹道倾角θ0的均值和方差,得到最终验证结果如图15∼16 所示.通过实验可得,该方法能够度量仿真模型不确定参数取值的离散程度对验证结果的影响,证明过大或过小的参数不确定度均会降低模型的可信度;同时该方法能够度量不确定性参数的均值差异对验证结果的影响.综上所述,所提方法能够用于解决带有相关性的多元输出仿真结果验证问题.
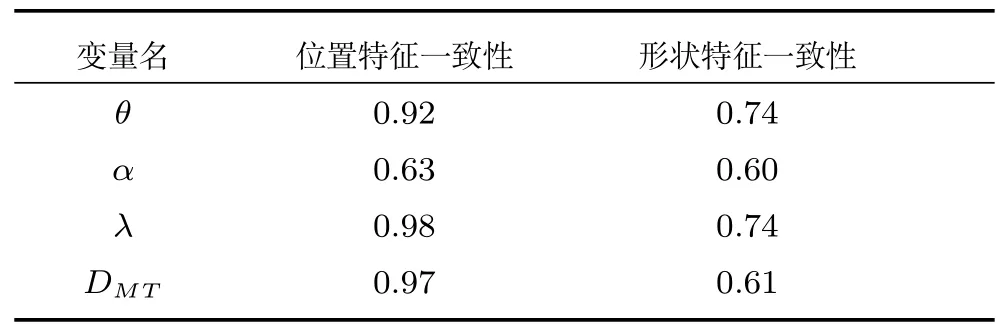
表5 动态输出均值曲线的一致性分析结果Table 5 Consistency analysis results of the mean curves of dynamic outputs
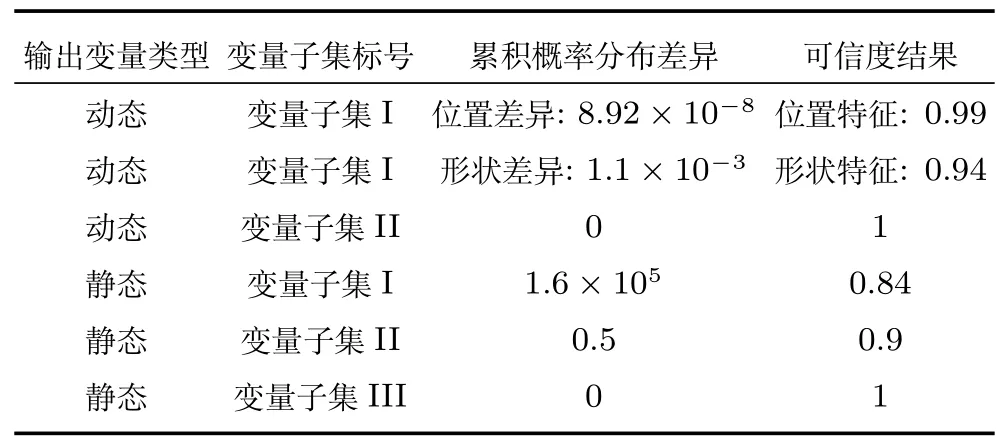
表6 仿真和参考输出变量子集的一致性分析结果Table 6 Consistency analysis results of the variables subset of the simulation and reference outputs
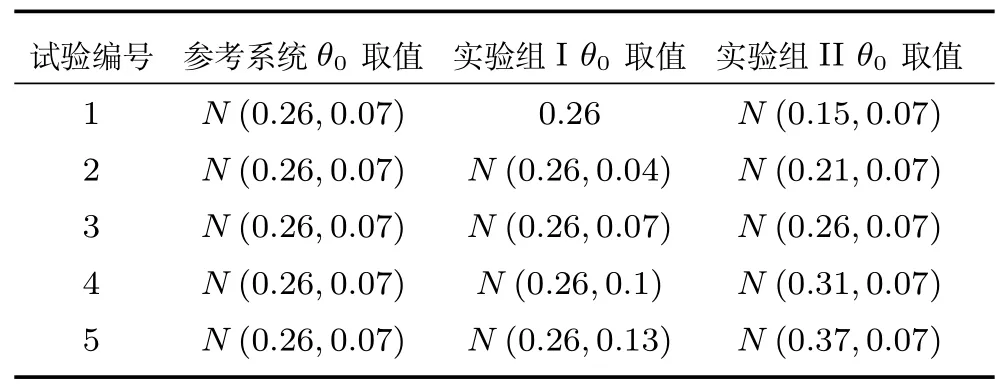
表7 验证实验的不确定参数取值Table 7 Uncertainty parameters values for validation experiments
5 结论
针对带有相关性的多元输出仿真模型验证问题,提出了考虑不确定性的联合验证方法.首先对多变量输出提取相关变量子集,并对各输出变量提取数据特征,利用联合CDF 差异法度量各相关变量子集的一致性程度,进而综合得到模型可信度.利用单变量验证方法进行多变量验证时需要满足输出变量相互独立的条件.本文方法考虑了多变量间的相关关系,基于相关变量子集进行联合验证,较单变量验证方法应用更合理;同时在验证前引入了变量相关性分析,使其能够适应输出变量之间关系未知的情况,使验证结果更准确,但也增加了计算开销.此外,该方法能够度量不确定性因素对模型可信度的影响.
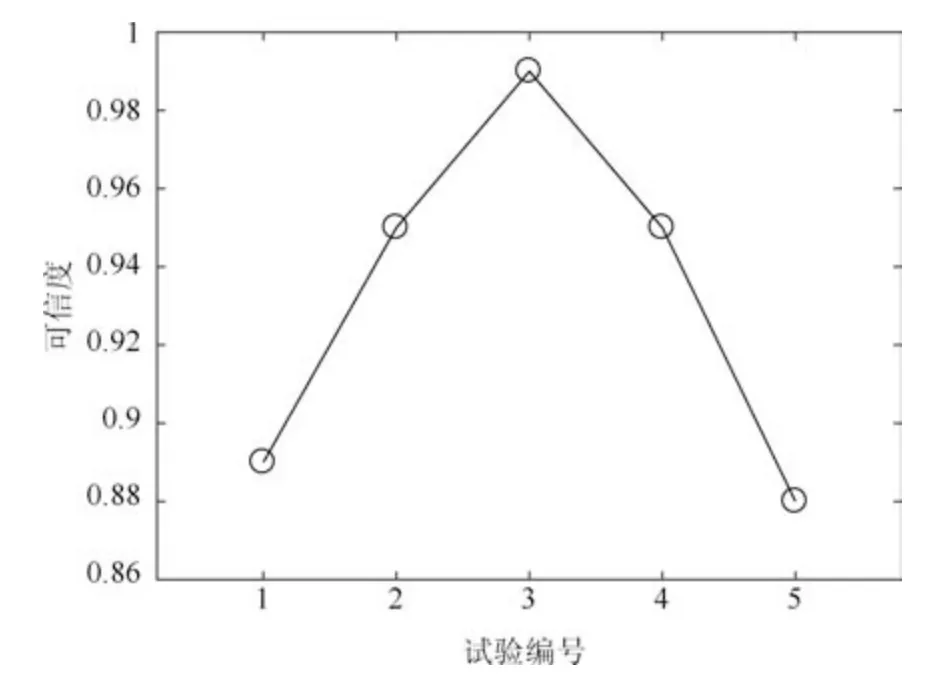
图15 实验组I 验证结果Fig.15 Validation result of experiment I
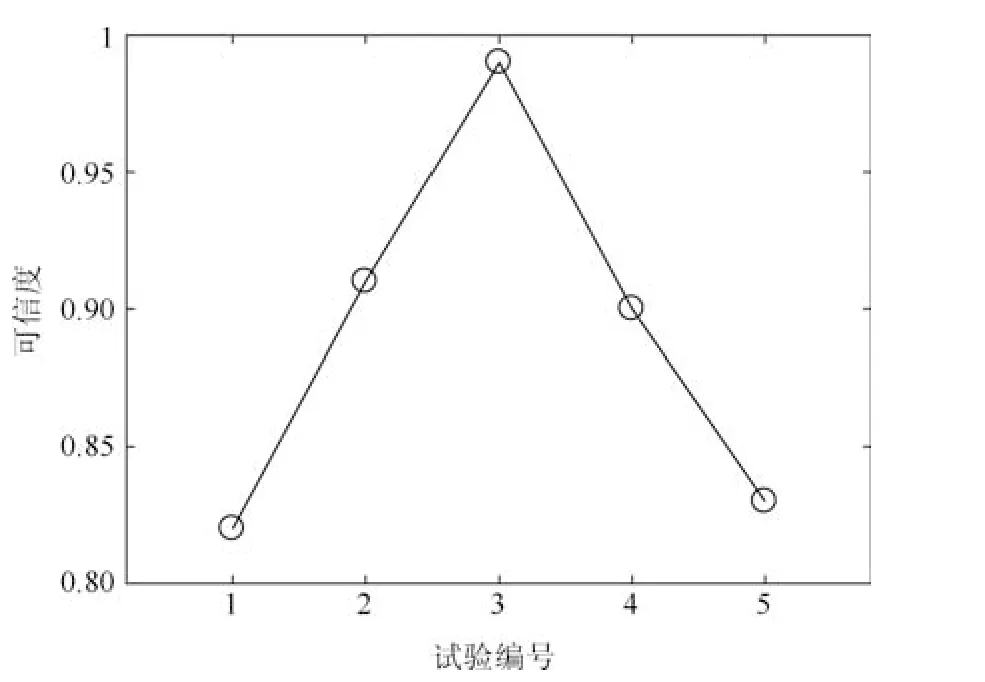
图16 实验组II 验证结果Fig.16 Validation result of experiment II
需要说明的是,本文仅考虑同一类型输出(动态或静态)存在相关性的情况,涉及的变量选择方法本质上属于数据挖掘方法,为确保方法的准确性要求具备足够的样本容量,对于参考数据缺乏的情况,可采用专家给出参考数据的大致分布,或可利用已有的历史数据、可信度较高且类似的半实物/纯数字仿真模型所产生的数据代替.此外,刻画动态输出的数据特征不限于距离、形状及频谱,可依据具体应用需求而定(例如,超调量、相位误差等).后续将对动态、静态输出间的相关性分析及变量选择方法进行研究;同时针对参考数据缺乏以及存在认知和固有混合不确定性时的多元输出仿真结果验证问题展开进一步研究.

