有混合数据输入的自适应模糊神经推理系统
张宇献 郭佳强 钱小毅 王建辉
随着全球数据量出现爆炸式增长,数据成了当今社会增长最快的资源之一.如何对大量复杂数据进行分析和挖掘,从中提取有价值的知识用于决策,已经成为学术界和产业界广泛关注的问题[1−2].在各行业中数据分析与数据建模仍有许多核心技术问题有待解决[3−4].如商业金融领域,电子商务企业通过对所销售产品的类别以及客户的浏览行为进行数据分析,进而精准把握客户的购买意图,其中数据信息中既包含数量、单价这样的数值信息,又包含商品种类、属性这样的非数值信息.银行金融企业对储户分类进行分析,根据客户特点对其设计不同的金融管理方案,其中数据信息中既包含账户余额、资金流量这样的数值信息,也包含储户年龄区间、职业、性别等非数值信息.又如工业生产领域,钢铁行业炼钢过程通过生产工艺参数建立生产过程数据模型对产量、产品质量、能耗等指标进行估计,其中工艺参数中既包含氧气压力、流量等数值数据,也包含造渣原料种类(如石灰、白云石和萤石等)带有分类性质的非数值数据.汽车行业电动汽车电池管理系统通过电池组运行数据对电池组状态和汽车续航里程进行估计,其中既包含电流、电压、内阻、温度等数值数据,也包含电池结构、电池类型等非数值数据.再如医疗领域中,医疗辅助诊断借助医院综合管理信息系统数据进行大数据挖掘给出患者的诊断和治疗方案建议,其中医学数据中既包含化验结果、基因数据等数值数据,同时也包含波形信号、图像、文字等非数值数据.上述领域中普遍存在一个共同特点,即数据信息中同时包含数值/非数值两类数据(这里我们将非数值数据统称为分类数据).
然而,现有数据建模方法大多依赖于定量的数值信息,难以加入定性的分类信息.对此国内外学者进行了大胆的尝试,并取得了一些进展.Jacobs等[5]利用多个独立网络子模型构建组合模型,采用有监督学习对模型参数进行训练.其子模型中仅包含数值变量,各子模型由分类变量组合成完整数据模型.但当分类属性值较多时,不同分类变量的组合排序将呈几何倍数增长.Lee 等[6]构建了多个参数的组合模型,每个子模型输入仅有数值数据.该方法采用1-out-of-n编码,把子模型中分类数据编码为一个数值向量,然后把该向量导入神经网络.然而当训练数据分布不均匀时无法精确描述模型.Brouwer[7−8]提出基于多层感知机(Multi layer perception,MLP)结构的改进神经网络模型,该模型由多感知机和多输出编码器单元组成.模型输入为数值变量,由分类变量决定最终模型输出,即每一个输出单元对应一个分类输入变量组合.该方法适用于分类变量较少的数据建模问题,当分类变量数量较大时该方法训练结构参数的时间较长.Reydel-Castillo 等[9]提出一种模糊极小极大神经网络,由模糊超立方体聚集形成的集合体定义模糊集,模糊超立方体的极大点作为模糊操作算子,并利用改进模糊极小极大神经网络模型结构实现数值/分类混合属性数据建模.但由于神经网络的黑箱结构,模型的输入输出映射关系难以解释.Hsu[10]采用自组织神经网络(Self-organizing map,SOM)结构,通过定义分类数据之间的距离把分类数据转化为数值数据.张宇献等[11]以自组织映射神经网络为框架,采用基于样本概率的异构值差度量混合属性数据的相异性.利用分类特征项在Voronoi 集合中出现频率作为分类属性数据参考向量更新规则的基础,通过混合更新规则实现数值属性和分类属性数据规则的更新.
尽管上述研究工作在数值/分类混合的数据建模中做出了积极贡献,但对于数值/分类混合的数据建模研究中仍有一些难点问题尚未得到很好的解决,具体体现在以下几方面:1)多个分类变量采用排列组合方式参与数值数据计算时,不同分类变量的组合排序将呈几何倍数增长;2)按分类变量建立多个子模型,各子模型训练数据分布不均匀;3)将分类变量转化为二进制数或定义成数值变量,参与计算时易出现大数吃小数现象;4)分类数据转化为数值数据的过程,忽略了各变量值之间内在的分类或约束关系.
针对上述问题,Liu 等[12]提出带分类输入的自适应模糊推理系统(Adaptive network-based fuzzy inference system with categorical inputs,C-ANFIS)结构,将激励强度转移矩阵(Firingstrength transform matrix,FTM)引入自适应模糊推理系统(Adaptive network-based fuzzy inference system,ANFIS)中,把分类数据对规则的影响作用到规则前件的激励强度上.该方法一定程度上取得了不错的效果,但它却存在自身不足:CANFIS 只考虑分类数据对规则前件的影响,而对规则后件并未做任何处理.基于以上分析,本文提出了一种具有混合数据输入的自适应模糊推理系统
(Adaptive network-based fuzzy inference system with mixed data inputs,MDI-ANFIS)模型.该模型在标准ANFIS 结构基础上,引入激励强度转移矩阵和后件影响矩阵(Consequent influence matrix,CIM),通过后件影响矩阵把分类数据对模糊规则后件的影响作用到ANFIS 上,使分类数据对整个模糊规则产生影响,并提出适应MDI-ANFIS 结构的参数学习算法.同时,针对MDI-ANFIS 结构辨识问题,给出了基于高氏距离的减法聚类算法,通过在减法聚类中引入混合型数据的高氏距离来确定MDI-ANFIS 的模糊规则数和规则前后件的初始参数.
1 MDI-ANFIS 模型
1.1 MDI-ANFIS 的网络结构
学者Jang 于1993 年提出了ANFIS[13],它融合了神经网络的学习机制和模糊系统的语言推理能力等优点,弥补各自不足,属于神经模糊系统的一种.ANFIS 能够以任意精度逼近非线性函数,具有便捷高效的特点,并已在多个领域取得了成功应用[14−18].
然而,标准的ANFIS 结构只针对数值数据输入,当输入有分类数据时利用标准ANFIS 建模将变得不再适合.例如,针对混合数据的自适应神经模糊推理建模问题,假设ANFIS 中的第l条规则有2 个数值输入和1 个分类输入,其规则描述如下:
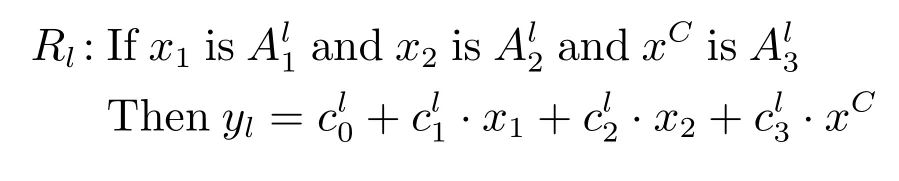
其中,x1和x2是数值数据输入,xC是分类数据输入,是第l条规则对应的模糊子集,yl是第l条规则的后件输出.
因为xC是分类数据,在规则中的和不能直接计算.
针对这个问题,本文提出一种具有混合数据输入的自适应模糊推理系统(MDI-ANFIS)模型,它在C-ANFIS 的基础上,引入后件影响矩阵,使分类数据对规则前件和后件同时产生影响,使得其对混合数据输入作用更加完善.
图1 是一个多输入单输出的MDI-ANFIS 结构图,其对应的第l条模糊规则为:

其中,xN=(x1,x2,···,xn)T为数值数据输入,为分类数据输入,n为数值输入变量个数,m为分类输入变量个数.为第i个数值输入对应的第j个模糊子集(为了表述方便在图1 中取j=1,2),s为分类数据的编码向量,为第l条规则的后件参数,pl为分类数据对第l条规则的后件影响,yl为第l条规则的后件输出,l=1,2,···,L,L为规则数.
MDI-ANFIS 网络结构分为6 层:输入层、规则层、正规化层、混合激励层、结论层和输出层,具体各层的输出为:
第1 层:输入层,该层的节点执行模糊化操作,把数值输入转化为模糊子集的隶属度值.各节点的输出可表示为
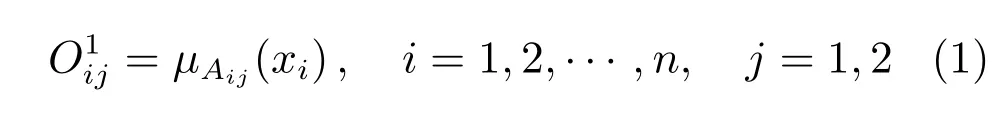
其中,µAij(xi)为输入变量xi的第j个模糊子集的隶属度函数,当取高斯隶属度函数时,其表达式为:


图1 MDI-ANFIS 结构Fig.1 Structure of MDI-ANFIS
其中,{cij,σij}(i=1,2,···,n,j=1,2)为模糊规则的前件参数集.
第2 层:规则层,该层节点执行规则前件数值变量的模糊与运算,计算出第l条规则数值变量的激励强度:
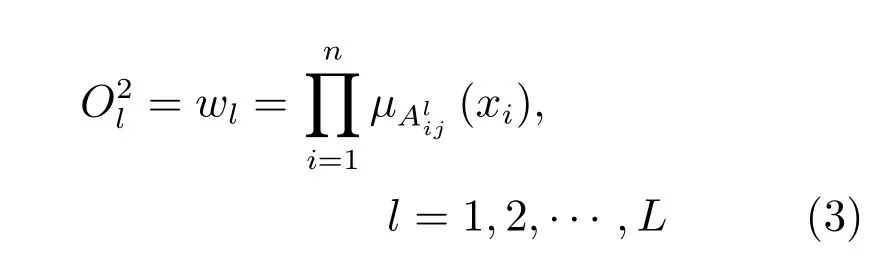
第3 层:正规化层,正规化规则层的激励强度.该层节点的输出为:
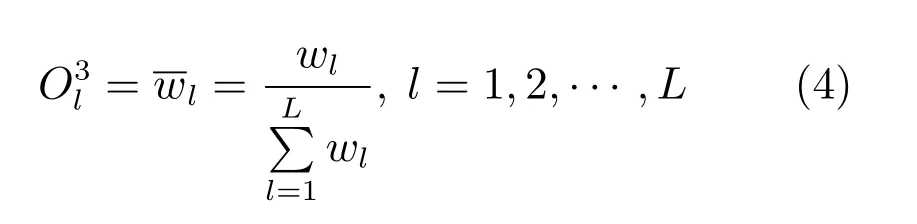
第4 层:混合激励层,该层节点计算分类数据和数值数据对每条规则的激励强度.各节点在该层的输出为:
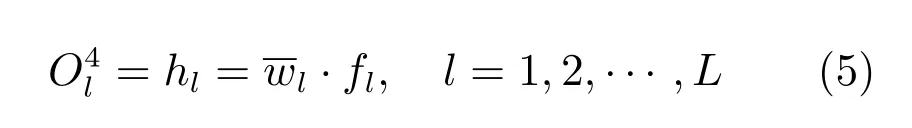
其中,fl为分类数据的编码向量经激励强度转移矩阵T得到的第l条规则上的分类激励值,fl=s·Tl,s为分类数据的编码向量,Tl为激励强度转移矩阵T的第l列.
第5 层:结论层,该层计算每条规则的输出.各节点函数是一个线性函数,各节点输出为:
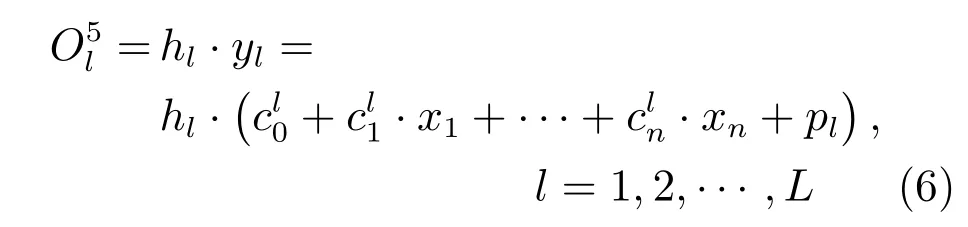
其中,pl为分类数据通过后件影响矩阵I得到的分类数据对每条规则的后件影响值,pl=s·Il,Il为后件影响矩阵I的第l列.
第6 层:输出层,计算整个MDI-ANFIS 的输出:
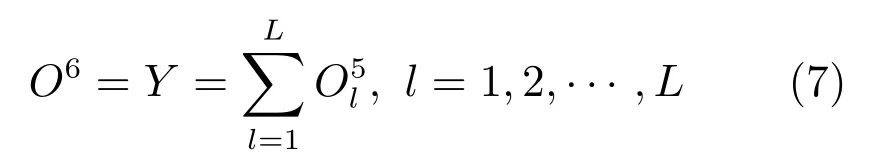
1.2 MDI-ANFIS 的参数学习
假设有K个训练样本点xk和sk(k=1,2,···,K)分别为第k个样本点的数值输入向量和分类编码向量,其中xk=(x1k,x2k,···,xik,···,xnk),xik为第i个数值变量在第k个样本上的取值.Yk为第k个样本点的训练输出值,为第k个样本点的期望输出值.对于单个样本点的MDI-ANFIS 的输出误差为
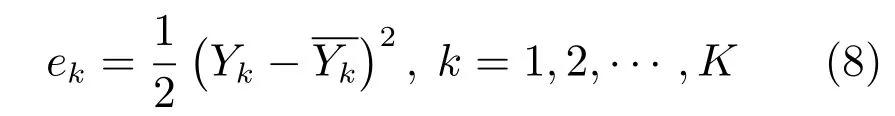
整个训练样本集的输出误差为:
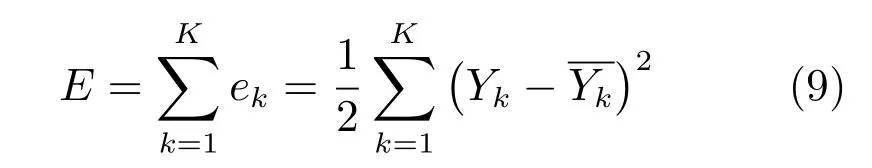
参数学习的目的是通过训练MDI-ANFIS 中的参数使总误差E达到最小.假定系统输入为第k个样本点,其输出为:

这里把所有由Cl元素组成的参数集合称为后件参数集Pc,所有由Il元素组成的参数集合称为后件影响矩阵参数集Pi.
将式(10)两边同时乘以[(zk)T·zk]−1·(zk)T,可以得到:
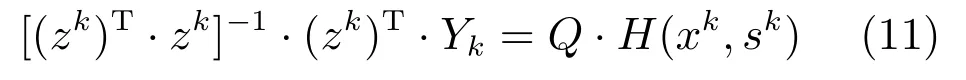
式(11)表明[(zk)T·zk]−1·(zk)T·Yk通过Q与H(xk,sk)成线性关系,而Q包含后件参数和后件影响矩阵参数,因此Pc和Pi可以通过最小二乘估计(Least squares estimation,LSE)得到.
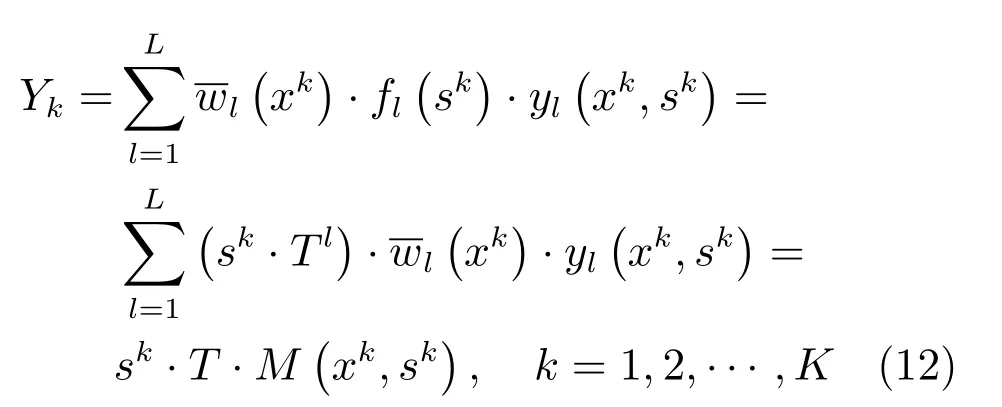
同理,在第k个样本点下的输出:yL(xk,sk)]T,Tl为激励强度转移矩阵T的第l列参数向量.
这里称由所有Tl元素组成的参数集合为激励强度转移矩阵参数集Pt.
将式(12)两边同时乘以[(sk)T·sk]−1·(sk)T,可以得到:
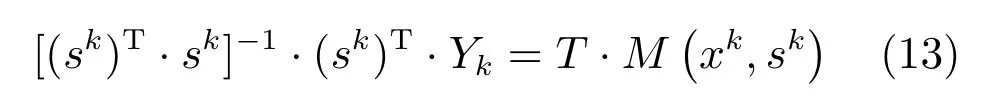
其中,
式(13)表明[(sk)T·sk]−1·(sk)T·Yk通过T与M(xk,sk)成线性关系,因此激励强度转移矩阵参数集Pt也可由LSE 得到.
以上有关Y k的所有推导中为MDIANFIS 正规化层的第l个输出,这里把所有中的参数组成的集合称为前件参数集Pp,它可以通过预先固定参数集Pt、Pc和Pi,然后由反向传播算法(Back propagation,BP)求得.MDI-ANFIS的参数学习步骤如表1 所示.

表1 MDI-ANFIS 混合学习算法Table 1 Hybrid learning algorithm of MDI-ANFIS
1.3 MDI-ANFIS 的结构辨识
当输入ANFIS 的维度不断增大时,采用传统的网格划分会使规则数目呈指数增大,这将不可避免导致维度灾难.本文提出了基于高氏距离的减法聚类算法(Gower distance-based subtractive cluster,GDSC)对其进行结构辨识.减法聚类(Subtractive cluster,SC)是一种无需预先确定聚类数和快速单次的聚类算法,克服了其他聚类算法的计算量随着输入维数的增加而呈指数增长的不足.然而,减法聚类只适用于对数值数据进行聚类,而对于混合数据就显得无能为力了,同时仅对混合数据的数值部分聚类产生的模糊推理结构也不完备,因为它没有考虑混合数据的分类部分对结构辨识产生的影响.基于以上减法聚类的优缺点,GDSC 算法把高氏距离引入到减法聚类公式中.这样GDSC 算法既充分利用了SC 的优势,又充分考虑到分类数据对结构辨识的影响.
结合文献[19]和[20],本文定义样本点Xk和Xr的高氏距离为:

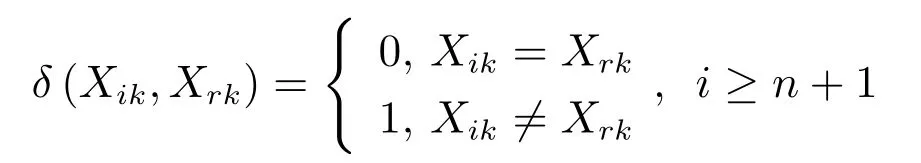
将式(14)代入到减法聚类公式中得到样本点的高氏密度

为排除已被选为聚类中心的附近数据作为下一个聚类中心的可能性,将式(15)的减法聚类密度修正为:

算法1.GDSC 算法

1.4 MDI-ANFIS 收敛性分析
本文针对基于MDI-ANFIS 网络结构的T-S 模糊系统,给出收敛性证明[21−22].基于MDI-ANFIS的T-S 模糊系统规则为:
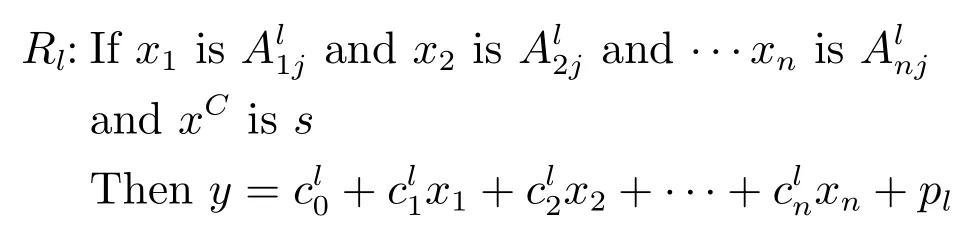
其中,xN=(x1,x2,···,xn)T为数值输入,xC=为分类输入,s为分类数据的编码向量,s ∈{s1,s2,···,sG},l=1,2,···,L,j=1,2,···,ni,此处ni为第i个变量的模糊子集个数,L为规则数,n为数值输入变量个数,m为分类输入变量个数.
其模糊子系统的规则为:
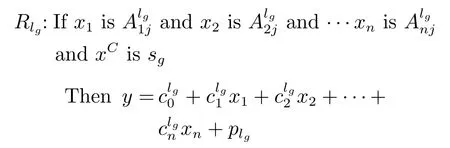
其中,Rlg为分类编码向量s=sg确定的模糊规则,lg=1,2,···,Lg.
这里,flg为子系统第lg条规则分类数据的激励强度,为子系统第lg条规则分类数据的后件影响值,为子系统第lg条规则的后件参数.
定义1.数值数据取值Cn[0,1],分类数据取值{s1,s2,···,sG}的φ次n+1 元多项式函数可以写为:

定义2.称论域U上的一组模糊集Aij(j=1,2,···,ni)是一致的,如果对某些xi0∈U存在使得且对任意υ=1,2,···,ni,以及=j,都有
假设1.所研究的T-S 模糊系统的每一个数值输入变量的模糊子集都是一致的.
假设2.所研究的T-S 模糊系统采用的隶属度函数都是连续且分段可微的.
假设3.所研究的T-S 模糊系统的每一个分类输入sg,sg·Tlg=1,其余=lg,sg·Tl=0.
基于上述假设,证明基于MDI-ANFIS 网络结构的T-S 模糊系统具有通用逼近性.
定理1.基于MDI-ANFIS 网络结构的T-S 模糊系统能够以任意精度一致逼近数值数据取值Cn[0,1]上,分类数据取值{s1,s2,···,sG}的φ次n+1 元多项式函数Pφ(xN,xC),即∀γ >0,存在T-S 模糊系统使得:
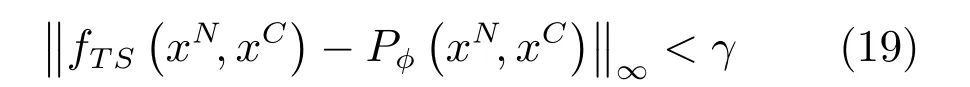
证明.假设T-S 模糊子系统的每一条规则Rlg,lg=1,2,···,Lg,它决定了一个特殊数值输入矢量xlg=(x1,x2,···,xn)T,每个分量xi(i=1,2,···,n)的取值恰好等于对应的模糊子集Algij的中心点,即

显然,对应一个T-S 模糊子系统,全部输入矢量共有Lg个,并且与子系统模糊规则一一对应的关系,记它们的集合为
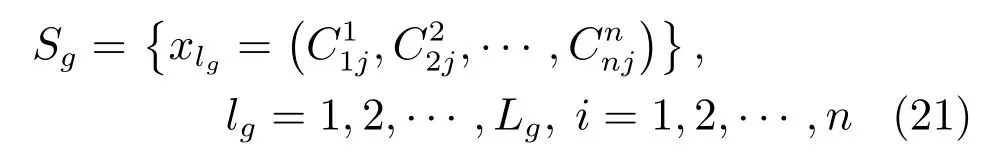
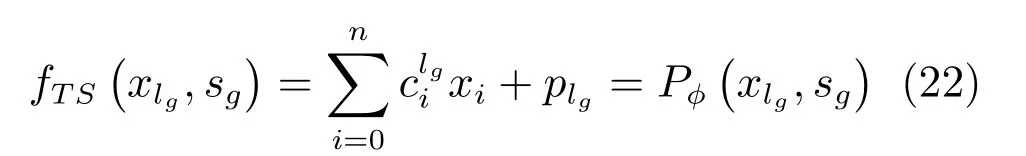
在fT S(xN,xC)中xN=(x1,x2,···,xn)T,并且令x0≡1.设数值输入变量xi(i=1,2,···,n)的第j个模糊子集的中心点为归一化xi(i=1,2,···,n)有不失一般性,设每个中心点处的隶属度为1,对每一个数值输入变量xi(i=1,2,···,n)定义模糊分割间距:

在此基础上可以对每个数值输入变量xi(i=1,2,···,n)定义最大模糊分割间距:

注意xN的任意分量xi(i=1,2,···,n),总可以找到下标j ∈{1,2,···,ni+1},使得从而
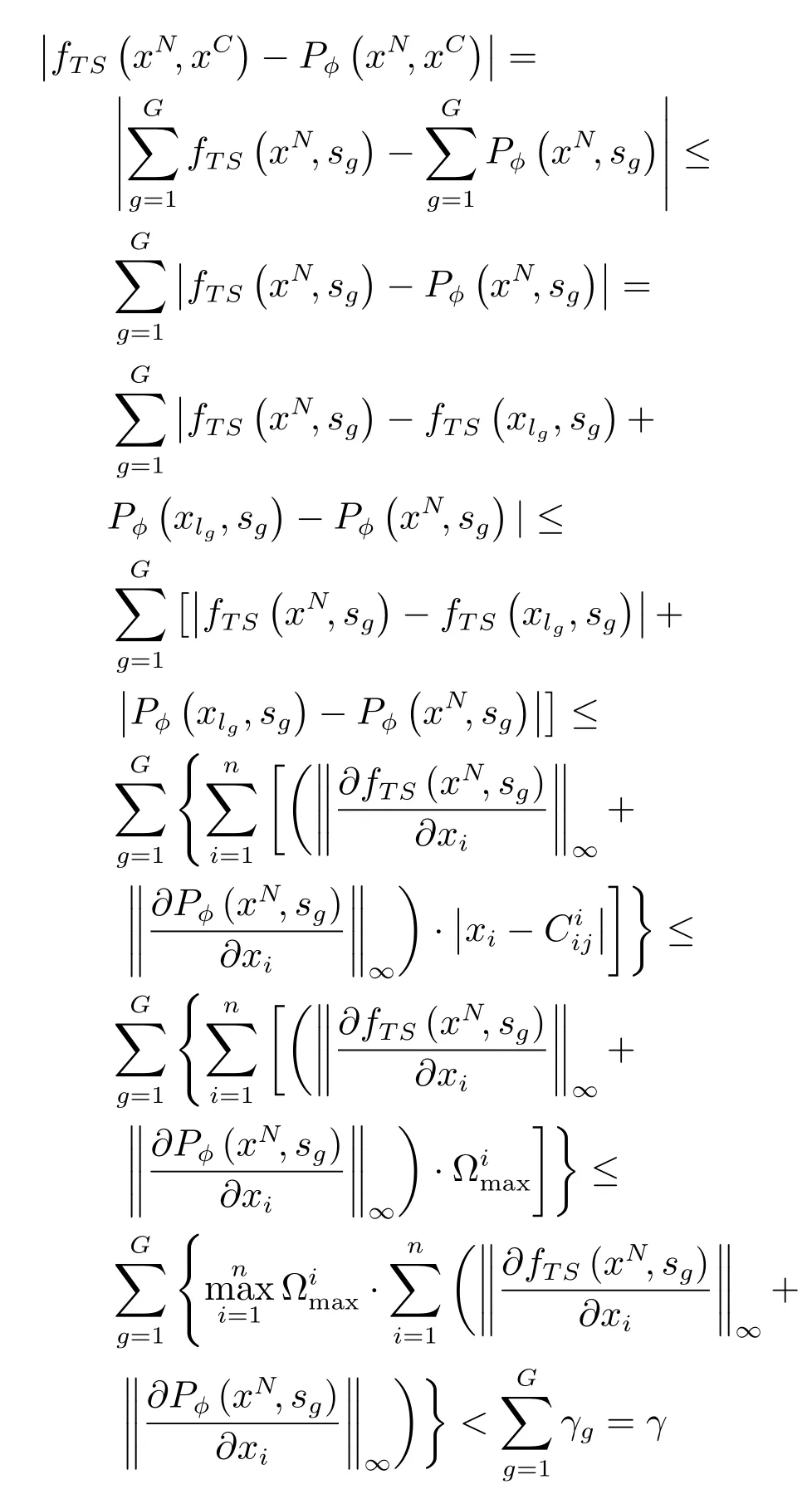
引理1.∀ζ >0,存在多项式P(x),使得对一切x ∈[a,b]的f(x)成立:
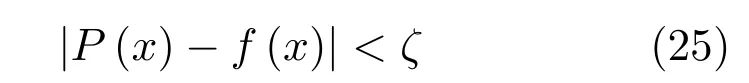
定理2.基于MDI-ANFIS 网络结构的T-S 模糊系统能够以任意精度一致逼近数值输入在紧致集U ⊂Rn上的任意实函数Ψ(xN,xC),即∀δ >0,存在基于MDI-ANFIS 网络结构的T-S 模糊系统使得:
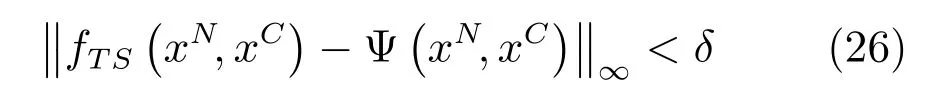
证明.根据引理,在U ⊂Rn上存在φ次多项式函数Pφ(xN,sg),一致逼近任意连续实函数ψ(xN,sg),即∀ζg >0 存在Pφ(xN,sg)使得另一方面,∀γg >0,根据定理1,存在
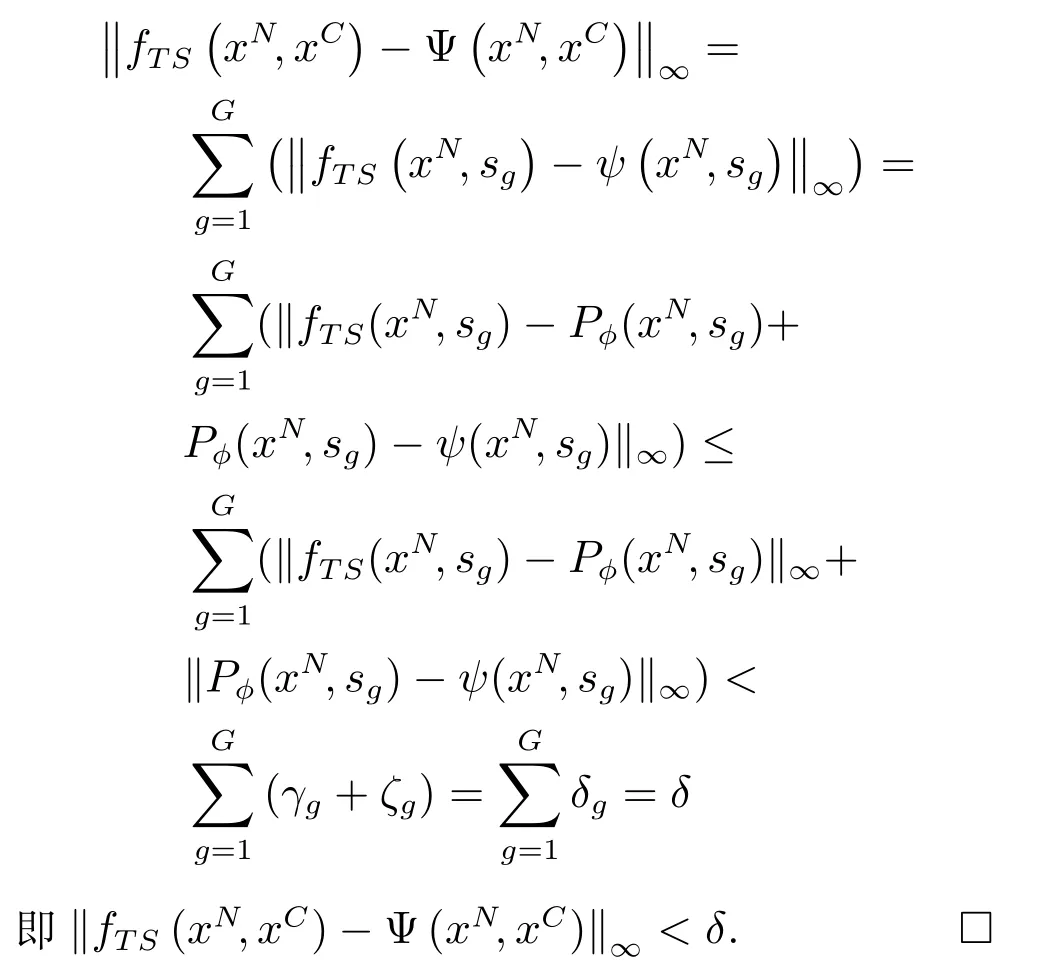
2 仿真实验及结果分析
为了验证所建模型的性能,我们将从规则后件参数影响分析、结构辨识方法比较以及几种混合数据建模方法预测精度对比几方面来说明本文所提出的MDI-ANFIS 的优越性.
实验操作系统为Windows 8.1,仿真软件为MATLAB 2009b.硬件条件:CPU 为Intel Core I5 2.5 GHz,内存为4 GB.
2.1 后件参数影响分析
对于参数预测问题,文献[12]提出的C-ANFIS算法把分类数据对规则的影响作用到规则前件上,但并未考虑其对后件的影响.本文在C-ANFIS 结构上做了改进,提出适用于混合数据参数预测的算法MDI-ANFIS,使混合数据中的分类数据对规则的前后件均产生影响.
这里采用UCI 机器学习库中的Abalone 数据集来训练C-ANFIS 和MDI-ANFIS 参数,然后预测鲍鱼的年龄.Abalone 数据集包含4 177 个样本点,分别记录了鲍鱼的性别、长度、直径、高度、整体重量、脱皮重量、内脏重量、壳重量和年龄属性值,其中鲍鱼的性别是分类属性数据,其他变量是数值属性数据.
表2 给出了两种算法对比结果,其中平均规则后件值反映了C-ANFIS 与MDI-ANFIS 对规则后件结论的影响大小,预测误差选取均方根误差作为误差指标.为了更加体现分类数据对规则后件的影响,我们选取表2 第1 组实验产生的平均规则后件值数据制作对比柱状图见图2,横坐标表示本组实验一共产生9 条规则,纵坐标记录了每条规则的平均输出值.图2 非常直观地显示出考虑分类数据对规则后件的影响将极大地改变规则后件大小.表2同时体现出MDI-ANFIS 相较C-ANFIS 能够有一个更好的预测精度.图3 是两种算法的训练误差对比,从图上可以看出随着训练周期的增加,两者的误差距离正在逐渐拉大.图4 是训练后的C-ANFIS模型和MDI-ANFIS 模型对测试样本点做预测的结果.对比结果显示相对于C-ANFIS 模型,本文所提出的MDI-ANFIS 模型在后件参数的影响和预测精度上更具优势.
2.2 结构辨识对比分析
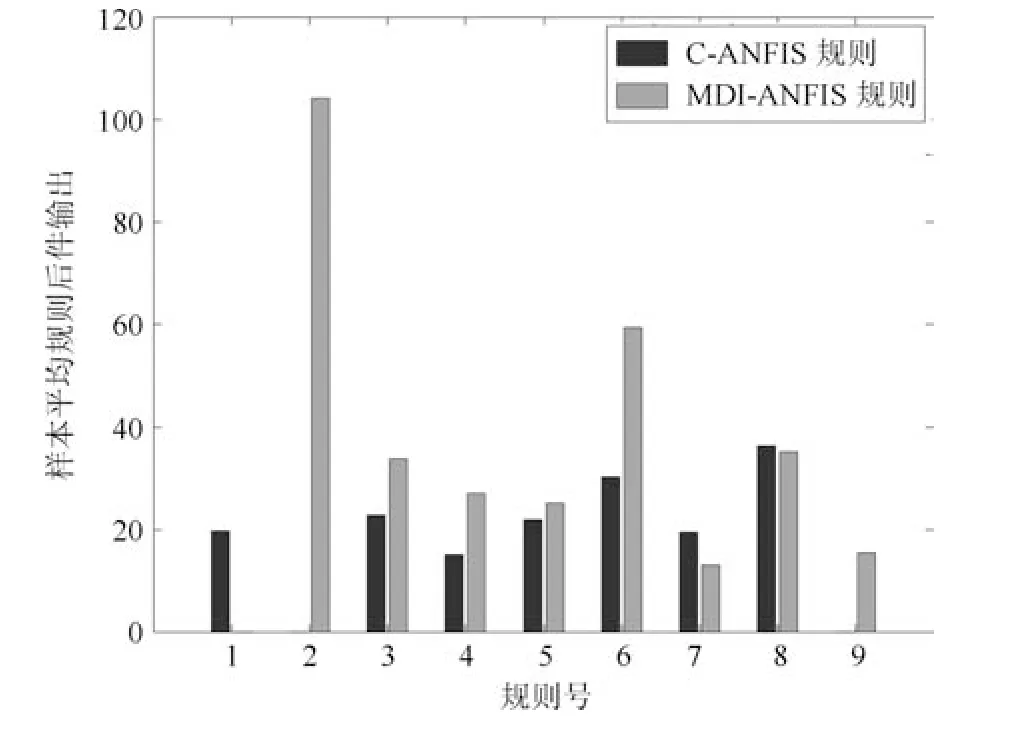
图2 样本平均规则后件输出Fig.2 Average consequent output of samples
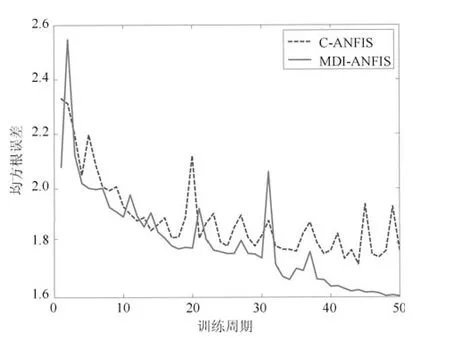
图3 模型训练误差对比Fig.3 Comparison of model training error

表2 两种算法的平均规则后件影响和误差Table 2 Average consequent influences and errors of two algorithms

图4 模型预测结果对比Fig.4 Comparison of model prediction
MDI-ANFIS 的结构辨识问题对具有高维输入数据的网络性能具有重要影响,本文提出的GDSC算法,将高氏距离引入到减法聚类中,实现数值数据和分类数据同时对初始规则产生影响,从而完成混合属性数据的ANFIS 结构辨识.实验采用UCI中的Boston Housing 数据集,它包含506 个样本点,其中11 个数值属性和2 个分类属性,这里把数值属性记为NA1∼NA11,分类属性记为CA1和CA2.实验首先利用SC 算法和GDSC 算法对Boston Housing 数据集聚类,然后利用聚类结果产生的规则作为MDI-ANFIS 的网络结构,再通过对MDI-ANFIS 进行训练得出模型来预测波士顿的房价.为了可视化方便,我们选取CA1=1,CA2={1,2,3}的样本点且使用平行坐标系显示(其结果见图5),图5 通过平行坐标系实现高维混合属性数据的可视化,从图中我们可以看出减法聚类得到的聚类中心数是12,聚类中心相对集中,存在一致性的问题.而基于高氏距离减法聚类得到的聚类中心数是4,且聚类中心位置分布相对比较合理.我们可以发现,GDSC 算法得出的聚类中心数比SC 算法得到的聚类中心数显著减小,且GDSC 算法得到的聚类中心更具代表性.
表3 从Boston Housing 数据集中随机选取10组样本集作训练对结构辨识性能对比,其中规则数反映出利用两种算法做辨识得到的规则数目多少,预测误差反映采用两种算法作结构辨识时模型的预测精度.通过10 组样本预测结果比较可以看出,两种辨识算法的预测误差平均值较为接近,但GDSC 算法在结构辨识中产生的规则较少,降低了需要训练的规则参数个数,因此模型的参数辨识速度相对较快.图6 是MDI-ANFIS 在第1 组数据下采用两种辨识算法做训练的模型训练误差,图7 是MDI-ANFIS 模型预测波士顿房价的结果.


图5 聚类结果对比图Fig.5 Comparison of clustering results

表3 结构辨识性能对比Table 3 Performance comparison of structure identification
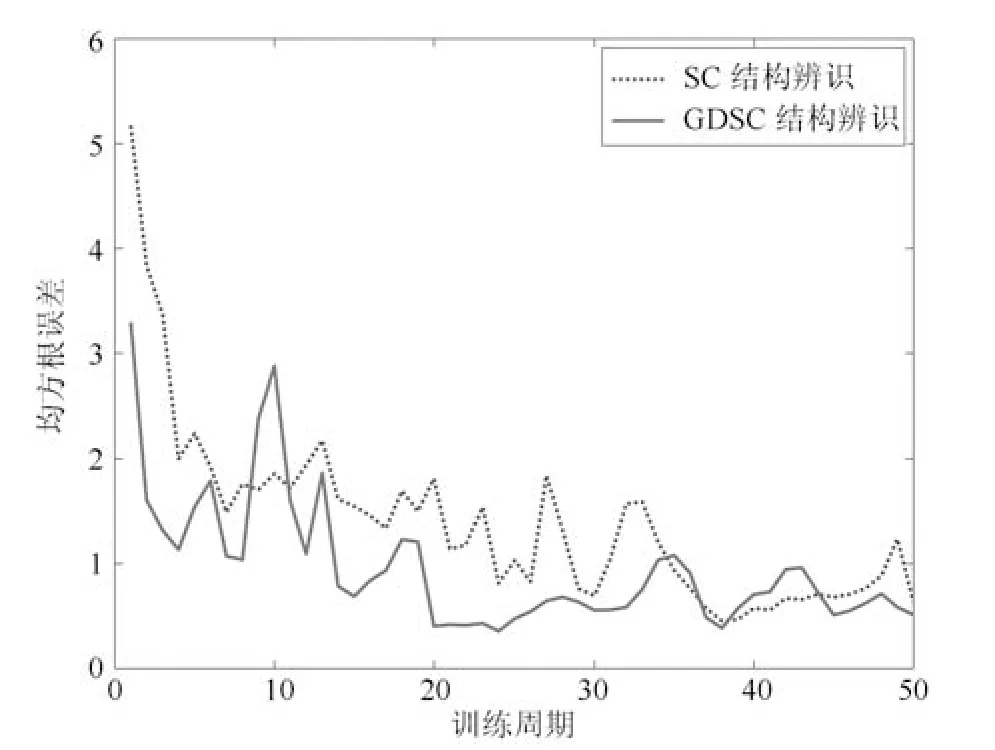
图6 模型训练误差Fig.6 Model training error
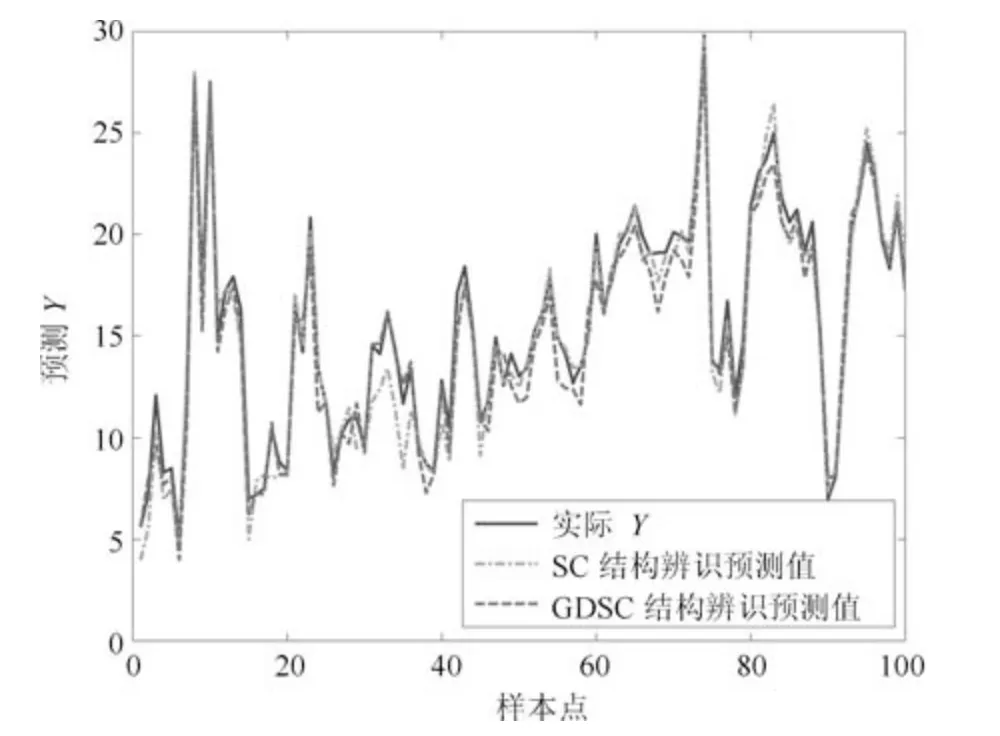
图7 MDI-ANFIS 模型预测对比Fig.7 Prediction results comparison of MDI-ANFIS
2.3 模型误差对比分析
为了比较分析MDI-ANFIS 模型在混合属性数据建模上的性能,现选取几种已有混合属性数据建模方法与之对比,对比建模方法说明如下:
1)ANFIS 模型:采用标准的ANFIS 算法,其中混合属性数据只考虑数值输入,而不考虑分类输入.
2)带有数值转化的自适应模糊推理系统(Adaptive network-based fuzzy inference system with numeric conversion,N-ANFIS)模型:将分类数据转化为数值数据(如1,2,3,···),然后和数值输入一起导入标准的ANFIS 网络中.
3)带有频率转化的自适应模糊推理系统(Adaptive network-based fuzzy inference system with frequency conversion,F-ANFIS)模型:通过频率给分类数据赋值,之后与数值输入导入ANFIS网络.
4)分离多层感知机(Multi-layer perception with separation method,S-MLP)模型:是由Brouwer 提出的混合属性数据预测模型,分类数据经编码后与以数值数据做输入的MLP 的输出作点乘,产生预测输出.
5)C-ANFIS 模型:是由Liu 等提出的CANFIS 混合属性数据预测模型,其分类数据经激励强度转移矩阵作用到ANFIS 结构上.
6)MDI-ANFIS 模型:本文所提出的混合属性数据预测模型,分类数据经激励强度转移矩阵和后件影响矩阵作用到ANFIS 上.
对比实验选取UCI 数据库中的Abalone、Boston Housing、Auto MPG、Servo、TAE、Zoo和Heart Disease 数据集,验证本文提出的算法对不同数据集的性能.
这里对ANFIS、N-ANFIS、F-ANFIS 和CANFIS 模型的结构辨识采用SC 算法;对MDIANFIS 模型的结构辨识采用GDSC 算法,其初始参数设置为:邻域半径表示样本点Xk和Xr的高氏距离,阈值ε=0.06,最大迭代次数L=100,训练周期epoch=50,初始化步长step=0.01,惯性因子gamma=0.75,激励强度转移矩阵FTM 和后件影响矩阵CIM 初始化为0∼1 区间的随机矩阵.而S-MLP 模型设置学习率deta=0.001,训练周期epoch=1 000,权值矩阵初始化为0∼1 区间的随机矩阵.
对比实验采用十折交叉验证,选取均方根误差(Root mean squared error,RMSE)为模型预测误差的评价指标.

其中,Yk为第k个样本点的预测输出值,为第k个样本点的期望输出值,K为样本点总数.
实验过程,记录每次测试集的RMSE,然后对十次测试得到的RMSE求其平均值,以此来判断模型对一种数据集的预测精度.
同时,本文还通过误差降低率(Error reduction rate,ERR)对各模型进行比较,其反映了各模型的RMSE相对原有模型下降的大小,误差降低率定义为:
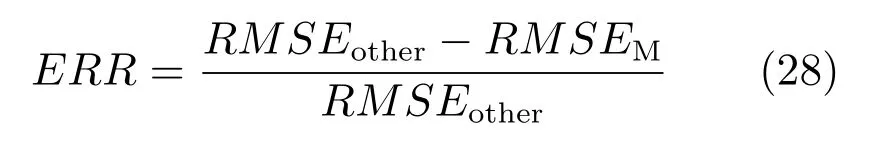
其中,RMSEM是MDI-ANFIS 模型的预测误差,RMSEother是本文对比的其他混合属性数据建模方法的预测误差.
表4 给出UCI 数据库中7 个数据集对应不同建模方法的预测误差以及误差降低率.通过几种建模方法的预测误差和误差降低率结果对比可以看出,对于不同数据集本文所提出的MDI-ANFIS 相对ANFIS、F-ANFIS、S-MLP 和C-ANFIS 具有相对较高的预测精度,仅相对于N-ANFIS 误差降低率较小.当对比7 个数据集的误差降低率平均值时,N-ANFIS 相对MDI-ANFIS 高出0.203.

表4 UCI 数据集模型误差对比Table 4 Model error comparison on UCI dataset
进一步我们对比N-ANFIS 和MDI-ANFIS 的计算时间复杂度,这里我们假设W为训练周期,K为样本点个数,n为数值属性个数,m为分类属性个数,L为规则数,则N-ANFIS 和MDI-ANFIS的时间复杂度分别为O(W ×K×(n+m)×L3)和O(W ×K ×n×L3),因此,在输入是高维混合属性数据时,MDI-ANFIS 的程序运行效率要高于N-ANFIS.
3 结论
本文针对已有混合数据模型存在的模型组合随分类变量呈几何增长以及子模型训练数据分布不均匀问题,提出一种具有混合数据输入的自适应模糊神经推理系统模型.该模型引入激励强度转移矩阵和后件影响矩阵,构建新型模糊神经网络结构,使混合属性数据对模糊规则的前后件同时产生影响.在模型的结构辨识中,将高氏混合距离引入减法聚类,计算混合型样本点的密度值,克服了经典ANFIS 网络仅适用于数值数据不适用分类数据的缺陷.在模型的参数学习中,使用BP 和LSE 混合学习算法来训练前件参数、激励强度转移矩阵、后件参数以及后件影响矩阵.仿真实验验证了后件规则对模型的影响作用,并验证了结构辨识中采用GDSC 算法能够以更少的规则数达到模型精度要求.最后,选取UCI 数据库中7 组数据进行对比实验,结果表明所提出的具有混合数据输入的自适应模糊神经推理系统模型相比其他模型具有更高的预测精度.

