基于变分的CT 图像环形伪影校正
霍其润 李建武 陆 耀 秦 明
计算机断层成像(Computed tomograpy,CT)技术作为一种高性能的无损检测手段在医疗等多种领域得到了广泛的应用[1−2].受实际成像系统的限制,重建后的CT 图像中通常会存在一些环形伪影,环形伪影的产生原因复杂,如何处理CT 图像中的环形伪影引起了业界广泛的关注.一部分研究[3−4]在数据采集时通过校正各探测器的响应率或是改变设备的扫描方式来避免环形伪影的出现,该类方法实现时存在一定的局限性和难度,且重建后生成的CT 图像中仍有残留伪影的可能.
近年来,基于图像处理的环形伪影校正方法研究取得了较大的进展,这类方法通过软件实现,实现代价较小,同时也可以达到较好的校正效果.该类方法又可划分为前处理方法和后处理方法两种.前处理方法是指在系统采集到投影数据后,通过对重建前的投影正弦图进行处理,来避免重建后CT 图像中出现环形伪影.Raven[5]提出在投影正弦图上使用傅里叶变换的方法.Münch 等[6]将小波分解和傅里叶变换下的低通滤波相结合,实现了将伪影信息与图像信息进行更为严格的区分.Ashrafuzzaman等[7]提出了自适应的可变窗口均值滤波用于正弦图中伪影的校正.Hasan 等[8]提出了基于形态学滤波的伪影检测和校正方法.Anas 等[9]通过对正弦图中的伪影进行检测实现分类校正.Rashid 等[10]将伪影根据不同的强度和宽度进行不同的处理.Kim等[11]通过计算投影图像域中各列数据间的比率来估计出各探测单元的不一致性并求出校正因子加以平衡,来实现伪影的去除.近些年还出现了一些结合压缩感知的方法作用在重建前的投影图像上[12−13]或图像重建的过程中[14]实现对伪影的抑制.虽然前处理方法的研究取得了很大的进展,但由于方法本身需要获取原始的投影数据,故其应用会受到一定的限制.后处理方法就是对重建后的CT 图像进行直接处理来实现伪影去除的效果.Sijbers 等[15]在CT 图像中提取出伪影较为明显的感兴趣区域,然后在极坐标系下利用滑动窗口对伪影进行滤除.Prell等[16]提出了一种结合均值和中值滤波的高分辨率CT 图像伪影去除算法,并通过比较说明将该算法作用于极坐标系下的重建图像校正效果更佳.Wei等[17]将Münch 等所提方法[6]用于重建图像上,在极坐标系下对图像进行小波分解和傅里叶低通滤波来实现伪影的校正工作.Yan 等[18]提出了稀疏约束的模型用于极坐标系下的重建图像来实现对伪影的校正.和作用在投影正弦图的前处理方法相比较,后处理方法由于是直接作用于重建后的CT 图像,校正效果更加直观,且实现时无需使用扫描过程中采集的原始投影数据,使用更加方便,应用场合也不受限制,无论是在成像环节还是在后续的使用环节,都可以使用基于重建图像的后处理方法来进行伪影校正,具有更好的应用前景.目前后处理的伪影校正研究受到了越来越多的关注[19−21],本论文工作也是从后处理的角度进行研究的.
目前较为成熟的校正方法中常用的一些频域或空域滤波方式,在去除伪影的过程中不可避免会对图像中的边缘信息产生一定的影响,图像一些原始的细节信息也可能会丢失,因此在不损失图像信息的情况下进行环形伪影的去除仍然是一个很有挑战性的任务.近年来基于变分的相关方法在图像去噪、复原等领域取得了很大进展[22−25],该类方法的优势是在去除噪声或干扰的同时能够较好地保护边缘信息,故本文基于变分的思想,把环形伪影校正问题转化为一个能量优化的问题来进行建模和解决,尽可能缓解保持图像信息和去除伪影之间的矛盾;同时考虑到CT 图像的环形伪影并非普通意义上的噪声,结合CT 图像环形伪影的产生机理和特征表现,设计有针对性的优化模型来有效地去除环形伪影,从而得到更高质量的CT 图像.与大多数后处理方法类似,为了使处理更加简单有效,我们构造的模型和算法也是在极坐标系下对伪影进行分离的,本文的校正流程如图1 所示.整个过程中,作为核心步骤的分离伪影操作是在极坐标系下使用本文构造的变分模型对图像进行处理的,为了减少坐标变换操作对整体图像信息的影响,最后一步是在笛卡尔坐标系下从原始CT 图像中对得到的环形伪影成分直接进行减除的,这样就相当于在整个过程中仅伪影信息部分受到了两次坐标间变换操作的影响,而CT 图像中其他信息几乎没受到影响.

图1 本文的校正算法流程示意图Fig.1 The flow chart of the proposed method
本文的主要贡献如下:
1)分析环形伪影在极坐标系下的几何特性,提出了更适合的模型梯度保真形式,尽可能降低处理过程中图像其他细节信息的丢失.
2)分析并提出环形伪影与图像结构性信息的边缘特性差异,模型中引入对伪影信息更有针对性抑制作用的相对全变分约束形式,从而增强模型对图像结构性信息的保护.
本文后续内容安排如下:第1 节详细描述了基于变分方法的思想并结合CT 图像环形伪影的结构特性来构造伪影校正模型的过程;第2 节介绍了模型的优化求解思路及其伪影校正算法;第3 节分别在模拟数据和真实CT 图像上进行了实验和比较,并对实现效果进行了进一步分析;第4 节做出了最后的总结.
1 变分模型设计
变分方法的思想是将一幅二维图像看作是一个能量系统,当没有噪声或其他干扰信息时,认为图像是平滑的,其对应的能量也很小.因而在解决图像干扰问题时,可以建立一个能量函数模型,引入某些约束条件,通过求取这个能量函数的最小值来获取理想图像的估计,从而去除图像中的噪声和干扰.由Rudin 等首次提出的一种经典全变分模型[26],又称ROF 模型,形式如下:
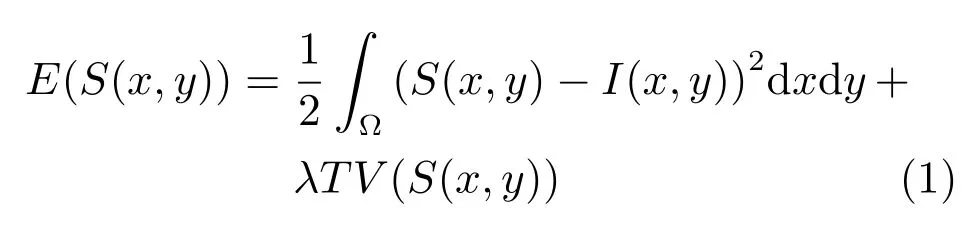
其中,(x,y)为像素点,I为初始的含噪声图像,S为处理后的平滑图像,Ω 代表图像域空间,式中采用了全变分(Total variation,TV)的约束形式:
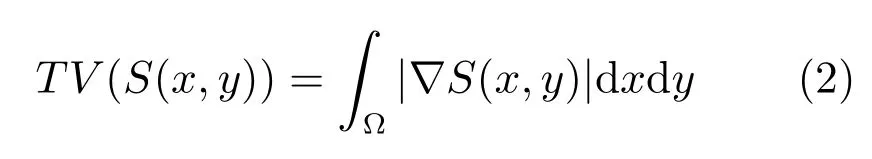
如式(1)所示,变分模型通常由保真项、正则项和正则化参数构成.模型中的第一项为保真项,其作用是保证处理后图像与带噪声的初始图像之间不要有太大的差别.第二项为正则项,也叫平滑项或约束项,其作用是去除噪声,使图像变得更加平滑,但同时也会使得图像信息在一定程度上有所损失.λ是用于平衡保真项和正则项的正则化系数,实际使用时通过合理选取正则化系数λ的值来达到图像去噪和保持图像信息之间的平衡.
对于CT 图像而言,环形伪影可以被看作是一种噪声污染,但是一种比较特殊的噪声形式,直接采用传统变分模型来处理显然不太适合,为了能够更有针对性地抑制环形伪影,我们结合环形伪影在实际CT 图像中的结构特性,来设计更为合理的能量函数模型,从而有效地实现对CT 环形伪影的校正.
1.1 环形伪影的几何特性分析及梯度保真设计
在笛卡尔坐标系下的CT 重建图像中,环形伪影表现为一系列圆心与重建图像中心相重合的同心圆环,为了降低伪影的提取与处理难度,我们可将待处理的CT 重建图像从笛卡尔坐标系转至极坐标系下进行处理.在极坐标系下,同心圆环的环形伪影就变成了平行的垂直条纹,如图2 所示.针对条带模式的噪声,许多不同领域也有着相关的研究,并根据自身特定的情况和应用产生了各种各样的方法[27−29].受这些方法的启发,我们对极坐标系下的伪影特性进行分析,设计更加有效的极坐标系下的去伪影模型.
在极坐标系下,包含伪影的CT 图像可以用数学公式表示为:

其中,I表示转至极坐标系下的CT 图像,即含有伪影的待处理图像,S表示极坐标系下不含伪影的理想图像,n为极坐标系下CT 图像中的伪影信息.如图2(b)所示,在极坐标系下伪影表现出了明显的垂直条状,因此可以被视为是一种有结构的特殊噪声,其引起的图像梯度变化主要表现在水平方向,而图像在垂直方向上受到的梯度干扰几乎为0,即

对式(3)分别在水平和垂直方向上求偏导可得:
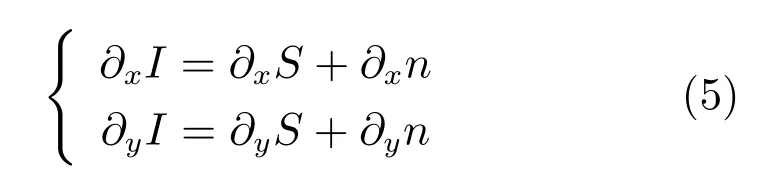
其中,∂x和∂y分别代表水平和垂直方向的梯度算子,在此由于I、S和n均为极坐标系下的图像信息,故式中x和y实际分别指示了图2(b)中的径向ρ和角度方向θ.结合式(4),故有:

由式(6)中描述的包含伪影图像的梯度情况可知,条状伪影很明显地影响了图像水平方向的梯度变化,对图像垂直方向的梯度变化影响甚微,因此在构造伪影校正模型时,我们可以利用这种鲜明的几何特性.
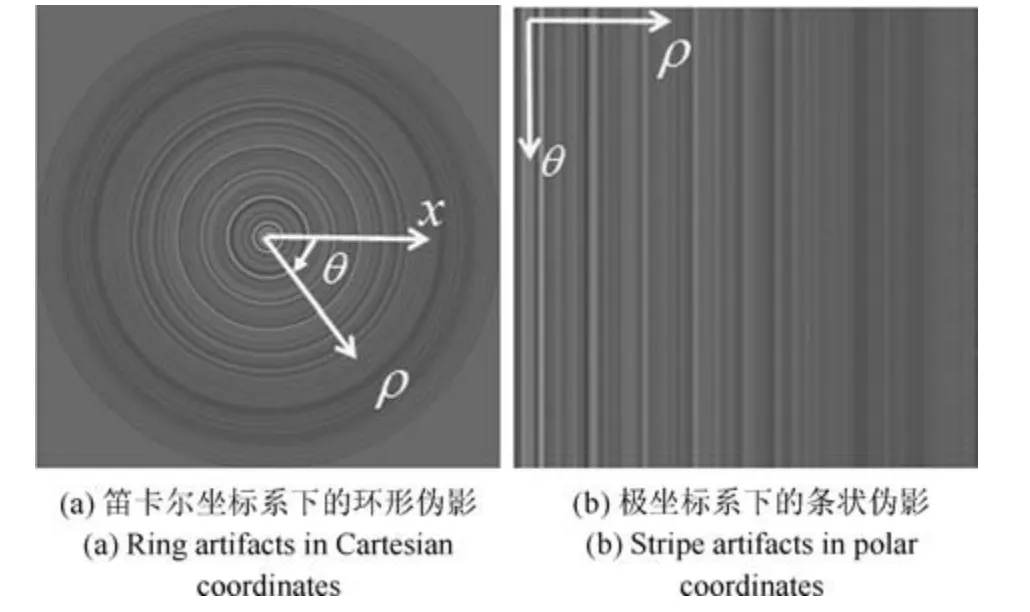
图2 极坐标转换Fig.2 Polar coordinate transformation
式(1)所示的传统ROF 模型中,第一项使用了图像处理前后像素灰度差的最小二乘形式来作为保真项,根据CT 图像的重建原理可知,在误差相差不大的情况下,靠近圆心的环形伪影将表现得更为明显,可见伪影的表现强度不满足高斯分布,根据研究者提出在去除非高斯加性噪声时,保真项采用L1范数形式比传统L2范数形式更有效[30−31],因此保真项可改为L1范数形式.此外,通过对环形伪影成因和实际医学CT 图像的分析可知,仅当CT 系统中出现了个别探测器通道损坏时,图像中会出现少量强度较大的单环伪影,对于这种情况通常可以通过硬件修复或图像检测等方法实现有效的处理,这部分不属于本文的研究范围;而大多数情况下由于探测器响应不一致等原因引起的多环伪影通常会具有相当的数量,虽表现强度不会太大,但伪影的去除势必会产生一定程度的图像灰度信息变化.根据上述伪影分析和式(6)中的描述,即理想情况下去除伪影后的结果图像对应的垂直梯度信息应与原图的基本保持一致,因此在设计模型时,利用保真项来限制图像处理前后垂直梯度信息尽可能不变更为合适,在此我们将常用的图像灰度保真修改为图像的单向梯度保真.第二项中用到的正则化约束是为了最大限度地去噪,普通的去噪处理要对图像中水平和垂直方向的梯度均进行约束,针对极坐标下伪影的单一方向性,去伪影时仅考虑一个方向的梯度约束即可,在此只对水平方向进行梯度约束.由此,可以得出以下基于梯度保真的变分模型形式:
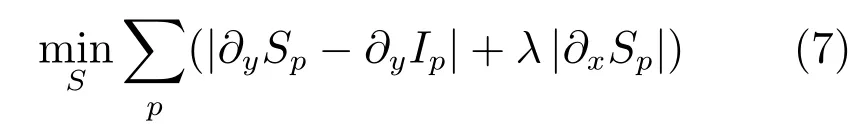
这里保真项和正则项中分别选用了垂直和水平两个不同的方向,第一项保真项用来保持图像在垂直方向的梯度信息,显然这些梯度主要来自图像本身的内容,因此更大程度地保留了图像的原始细节;第二项正则项中只对水平方向的梯度进行了约束,从而更有针对性地去除垂直伪影.
1.2 环形伪影的边缘特性分析及正则项设计
上述梯度保真模型(7)可以较好地保留垂直方向图像的原始细节信息,其中的正则项仅对图像水平方向的梯度进行了约束.但水平方向的梯度显然不是完全由垂直伪影引起的,其中也包含了图像本身内容的信息,因此在做约束时,若能将两者区分开,处理效果将会得到更有效的提升.
从环形伪影的成因和表现可知,连续多个探测器出现同样的响应异常是比较少见的,即环形伪影每个环的宽度有限,其灰度值与周围像素存在一定的差异,表现为较细的边缘形式.对于包含环形伪影的图像,其上的边缘信息有来自于图像本身的结构性信息,也有来自环形伪影的信息.按照边缘像素与其周围像素的灰度关系,图像中的边缘信息可大致分为两类:屋脊型边缘和阶跃型边缘.屋脊型边缘位于灰度增加与减少的交界处;阶跃型边缘在阶跃两边的灰度值有明显的变化.图3 为两类边缘剖面示意图,分别对应了两类边缘在垂直于边缘方向上可能出现的灰度变化趋势,其中横坐标表示垂直于边缘的方向,纵坐标表示像素值.环形伪影的每个环较细倾向为屋脊型边缘;而图像中的阶跃型边缘主要来自于图像结构性信息.相应两类边缘产生的图像梯度情况也有所不同,如图4 所示.在边缘所在的局部区域,一个屋脊型边缘产生的图像梯度既包含正向梯度也包含反向梯度;而一个阶跃型边缘产生的图像梯度通常方向是一致的,要么全为正,要么全为负.
根据上述对不同类型边缘的特性分析可以看出,环形伪影与图像结构性信息在产生图像局部梯度的效果上表现有明显的差异.在此要去除图像中的环形伪影,若能将环形伪影与结构性信息表现出的差异性引入到对图像梯度的正则约束项中,可以更有针对性地对伪影信息进行抑制,从而减少处理过程中对其他图像信息的影响.
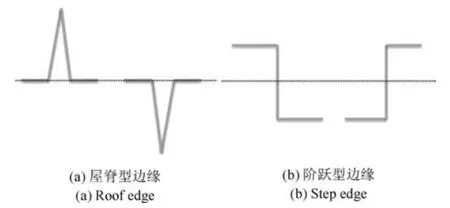
图3 边缘剖面示意图Fig.3 Edge profile diagram
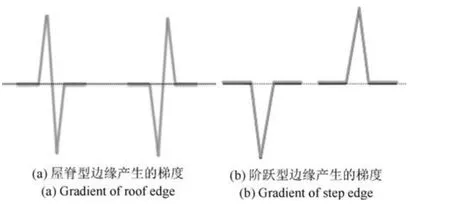
图4 两类边缘产生的梯度效果示意图Fig.4 Gradient diagram of two types of edges
受Xu 等在研究图像结构–纹理分离方法时提出的相 对全变分(Relative total variation,RTV)概念[32]的启发,发现相对全变分的计算结果能较好地体现出上述分析的差异性.在极坐标系下伪影表现为平行的垂直条纹,基于模型(7)的构造,第二项的正则项中只考虑约束图像水平方向的梯度变化.在水平方向上,图像中所有边缘均会产生梯度信息,由于各条垂直伪影宽度有限,为屋脊型边缘,其相关像素产生的局部水平梯度会有正有负,而图像结构性信息更多地倾向为阶跃型边缘,其相关像素产生的局部水平梯度方向是大体一致的.为突出对垂直伪影的约束,减少对图像结构信息的影响,我们结合相对全变分的定义,引入像素局部窗的单向相对全变分形式作为模型的正则项,实现伪影与图像内容更严格的分离,得到最终的目标函数如下所示:

其中,

式(8)中,ε取很小的正实数以免分母为0,R(p)表示图像中以像素p为中心的局部区域窗口,q为该局部窗中的像素点,gp,q为根据区域内各梯度所在位置定义的权重函数,表示如下:
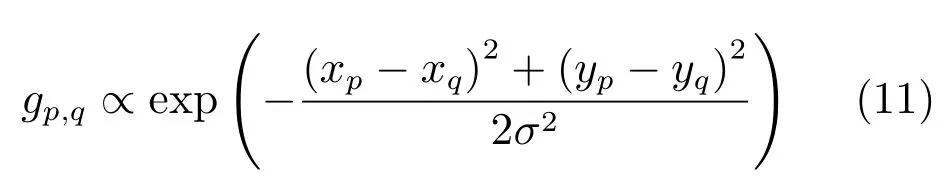
其中,σ控制了局部区域的窗口尺寸.Dx(p)是像素p在x方向的局部窗口全变分,它计算了R(p)中各点水平梯度绝对值的总和.无论是条状伪影还是图像的结构性信息边缘,都对应较大的Dx.Lx用来度量局部窗口内水平梯度的总体变化,在求和时未对窗口中各梯度单独取绝对值,故求得的总和大小取决于区域内各梯度是否具有一致的方向性.比较而言,倾向为屋脊型边缘的条状伪影更易使区域中的水平梯度出现有正有负的情况,倾向为阶跃型边缘的图像结构性信息会产生更多方向一致的水平梯度值,因此仅包含条状伪影的区域,其对应的Lx值通常小于包含图像结构性信息的区域.将Dx和Lx结合起来构成的水平方向相对全变分Dx(p)/(Lx(p)+ε)能够凸显出图像中的条状伪影信息(条状伪影信息Dx较大Lx较小;结构性信息Dx较大Lx也较大;平滑区域Dx和Lx均较小),故将其作为最小化模型中的正则约束项,如式(8)所示,可更好地满足仅对图像中条状伪影进行抑制的需求.
2 模型求解及其校正算法
式(8)所示的目标函数是非凸的,无法直接求解,由于二次项便于线性优化,我们参照文献[32]中给出的方法将公式中的RTV 约束项分解成一个非线性项和二次项的乘积形式,如下所示:

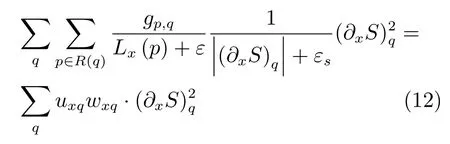
上述推导中的第三行为避免分母为0 添加了一个小的正实数εs,故为近似相等.可见约束项被分解为了二次项和非线性部分uxqwxq的乘积,其中
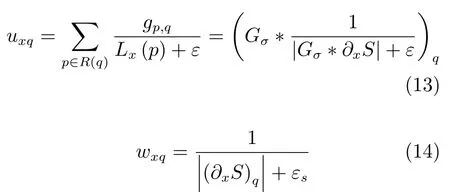
式(13)中求像素的ux时用到了周围区域的梯度信息,Gσ表示标准差为σ的高斯核函数,∗是一个卷积运算符,式中的除法为点除运算.式(14)中求像素的wx时计算比较简单,只涉及当前像素的梯度信息.
此外,近似可将式(8)中第一项进行如下转换:
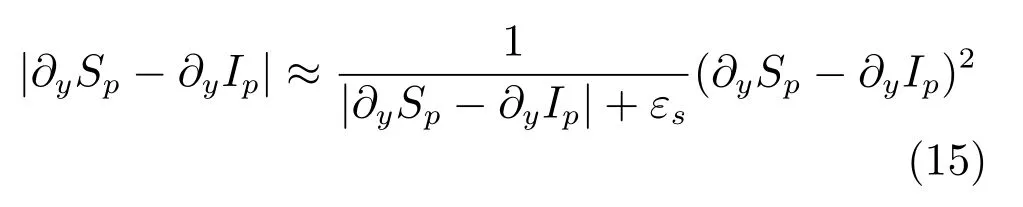
基于以上转换,式(8)相应可写为以下矩阵形式:

式中,R为一对角矩阵,对角线元素取值R[i,i]=1/(|∂y(Si −Ii)|+εs),vS和vI分别是图像S和I的列向量表示形式,Cx和Cy分别是在水平方向和垂直方向做前向差分的梯度算子矩阵,Ux和Wx均为对角矩阵,它们对角线元素的值分别为Ux[i,i]=uxi,Wx[i,i]=wxi.
要对式(16)求最小值,令其对vS求导为0,得到如下线性方程:
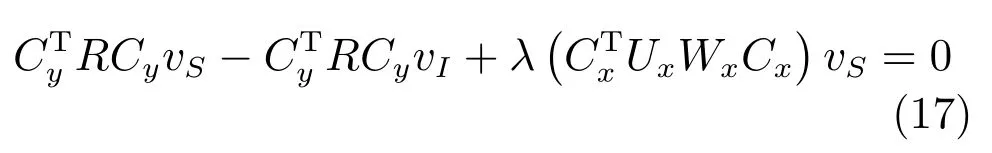
故有
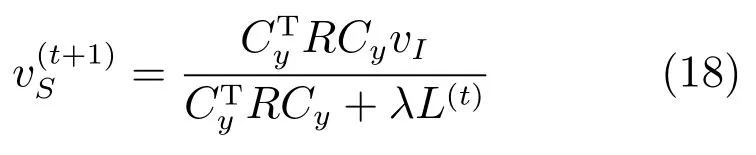
结合上述设计的模型及其求解过程,基于变分模型的CT 图像环形伪影校正算法描述如下:
算法1.基于变分模型的环形伪影校正算法
输入.含有环形伪影的CT 重建图像F,参数λ和σ
输出.去除伪影后的CT 图像R
1)将图像F转至极坐标下生成图像I
2)S(0)←I,t ←0,=1×10−3
3)repeat
基于S(t),利用式(13)和式(14)计算权值w和u,生成矩阵L(t);
基于L(t),利用式(18)计算,生成图像S(t+1);

4)条状伪影K=I −S
5)将K转至笛卡尔坐标系下生成环形伪影A
6)无伪影的结果图像R=F −A.
3 实验结果与分析
基于本文所提算法,我们分别在模拟数据图像和实际CT 图像上进行了伪影校正的有效性验证.实验中待处理初始图像均归一化为[0,1]的灰度图,在笛卡尔坐标系和极坐标系下的图像尺寸分别设定为512×512 和360×360.为了验证算法的有效性,我们在此选择了三个有代表性的后处理方法—WF[17]算法、RCP[16]算法和VDM[18]算法作为对比,其中WF 算法虽最初是基于投影正弦图设计的[6],由于作用原理相似,后续也被直接作用于转换至极坐标系下的CT 重建图像[17].由于这些方法都是在极坐标下对重建图像进行处理的,公平起见,我们实验中采用了统一的坐标转换方式.
3.1 模拟数据实验
为了客观地评价各种算法的性能,我们采用一些常用的定量评估方法来评价去除伪影后的图像效果,在此引入两种常用的图像评价指标:峰值信噪比(Peak signal-to-noise ratio,PSNR)和平均结构相似性(Mean structural similarity,MSSIM).PSNR是最普遍和使用最为广泛的一种图像质量评价指标,是基于对应像素点间的误差,将处理结果与参考图像的像素值进行比较,处理结果的PSNR 值越大说明与参考图像的像素值差异越小,即算法性能越好.MSSIM 是一种更接近于人类视觉的图像质量评测方法,指标值体现了处理结果与参考图像间的亮度、对比度以及结构的相似性,更多地与图像视觉特征相关,值越大说明处理结果视觉上越接近理想的参考图像.考虑上述评价指标计算时均需用到理想的无伪影图像做参考,而现实情况下,对于包含伪影的CT 图像,这些理想的参考图像往往无法获得,故在此使用人工生成的一些模拟数据进行实验.
我们首先采用的是Shepp-Logan 模型测试图,如图5 所示,其中包含许多均匀平滑的区域,便于对处理结果进行有效的观察.图5(a)为不包含伪影的标准参考图像,将人工模拟的环形伪影叠加在参考图像上生成了待处理的模拟图像,如图5(b).图5(c)显示了采用本文算法处理后的整体效果,图5(d)∼5(f)分别对应图5(a)∼5(c)中相同部分区域的放大显示效果,从中可以看出本文算法的处理效果视觉上非常接近理想的参考图像.图5(g)∼5(i)分别是WF、RCP 和VDM 三种算法的处理结果,可以看出WF 算法的处理结果(图5(g))中有新增伪影的出现,RCP 算法的处理结果(图5(h))中大部分伪影均被有效地去除了,但在图像中心位置处,由于伪影强度较大,校正后仍有一定的残留伪影存在.VDM 算法的处理结果(图5(i))视觉效果较好,仅从视觉上已看不出残留伪影的存在.除了视觉观察外,为了更客观地评价算法性能,我们基于参考图像,计算了各种算法处理结果对应的峰值信噪比PSNR 和平均结构相似性MSSIM,如表1所示.通过比较可以看出,本文算法较WF 和RCP两种算法,性能指标值提高明显,这也与之前的视觉观察的结果相一致;此外虽然本文算法与VDM 算法的处理结果在视觉比较中看不出太大的差异,但通过定量的性能指标计算,两者还是有一定的差异的,本文算法的处理结果对应了更高的峰值信噪比和平均结构相似性,结合视觉观察和定量指标的分析可以看出本文算法在去除伪影和保持图像信息方面具有更好的性能.
我们的第二组模拟数据选取了Lena 图像,如图6 所示,虽然该图像不是CT 图像,由于图像中既有平滑区域又包含丰富的边缘及纹理细节信息,在此选用可以更有效地体现处理过程对多种图像成分的影响效果.理想的无伪影图像如图6(a)所示,图6(b)为添加了环形伪影的待处理模拟图像,采用本文算法处理后的整体效果如图6(c)所示,视觉上看来伪影已被有效去除,同时图像中的细节信息也保留得很好.为了便于更清晰的视觉观察,取图6(a)∼6(c)中相同部分区域进行放大显示,依次对应图6(d)∼6(f)所示.图6(g)∼6(i)分别是WF、RCP 和VDM 三种算法的处理结果,总体上来看,各种算法均有效地去除了图像中的大部分伪影,同时也较好地保留了图像中的细节信息.但在某些局部区域,WF 算法和RCP 算法的处理结果中仍可看出有少量伪影的残留,如图6(g)和图6(h)中箭头所指位置.VDM 算法的处理结果明显好于WF和RCP 两种算法,基本看不出有残留伪影的存在,但和本文算法的处理结果比较起来,在一些灰度均匀的区域,如图6(i)中箭头所指的脸颊位置,其处理后的效果比较起来略显得有些粗糙,而本文算法的结果看起来更加平滑.通过表1 中所列的评价指标值可以看出,和其他三种算法比较起来,本文算法的处理结果具有最高的PSNR 和SSIM 值.
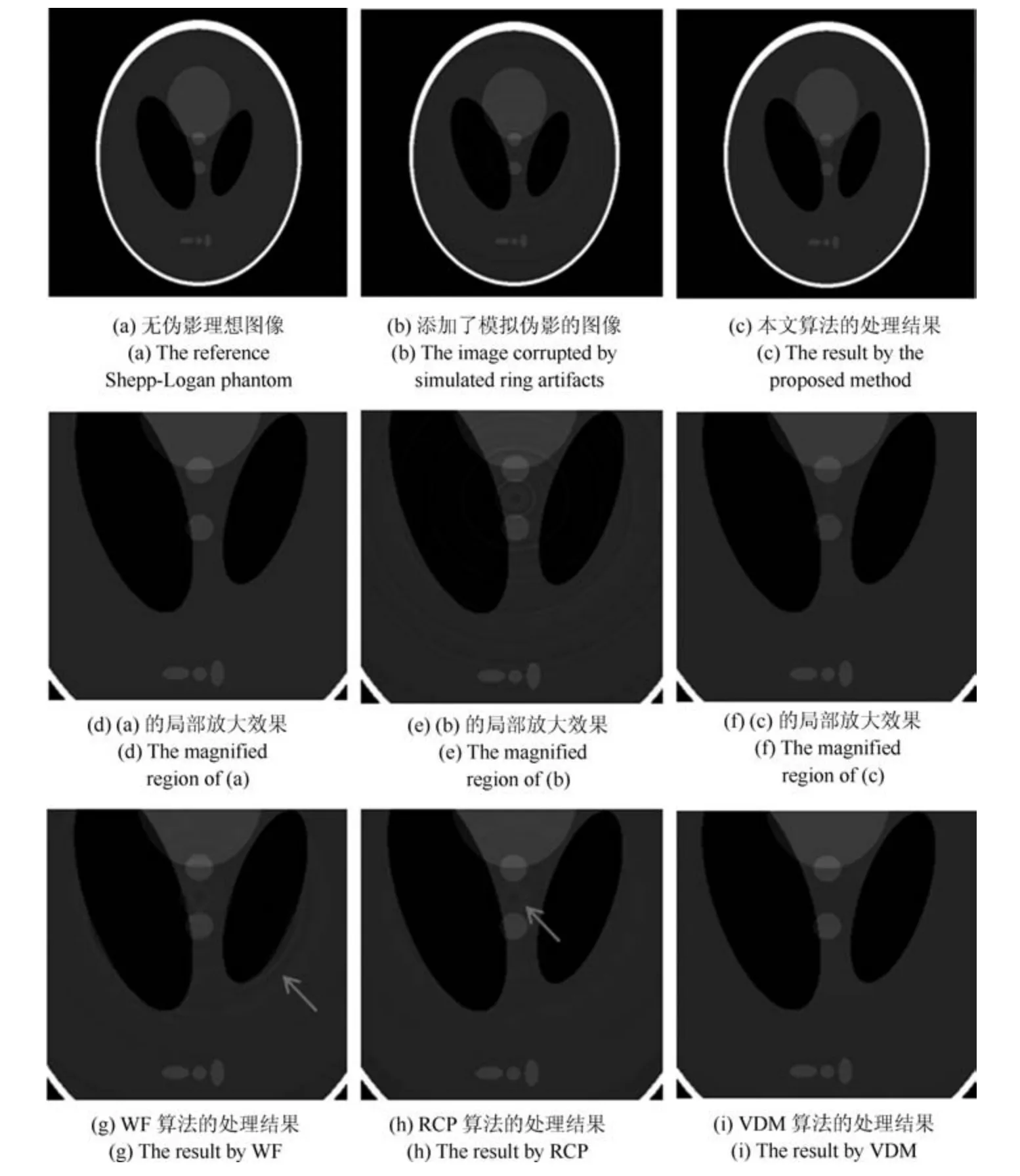
图5 Shepp-Logan 图像处理结果Fig.5 Experimental results on the Shepp-Logan phantom
3.2 真实数据实验
为了进一步验证本文算法的实际校正效果,我们利用上述几种校正算法对两幅真实CT 图像进行了去除伪影的处理,如图7 和图8 分别显示了一幅脑部CT 和一幅颈部CT 的各算法实验情况对比.

表1 各算法结果的图像质量评价指标值Table 1 Quantitative comparison for the different methods

图6 Lena 图像处理结果Fig.6 Experimental results on the Lena image
在这两组实验图中,图7(a)和图8(a)为处理前的原始图像,在此为了让环形伪影看起来更明显,我们适当地增强了图像的对比度.可以看出在接近图像中心位置有较强的伪影,偏离中心的位置上伪影强度较弱.图7(b)和图8(b)分别是图7(a)和图8(a)中局部区域的放大效果,图7(c)∼7(f)和图8(c)∼8(f)依次放大显示了四种算法处理结果中的对应区域.图7(c)为本文算法的处理结果,环形伪影没有明显的残留,同时图像结构及平滑度均得到了较好的保留.图7(d)和图8(d)是WF 处理的效果,可以看出靠近图像中心的环形伪影去除的较好,但在偏离中心的位置会有一些新的伪影出现.图7(e)和图8(e)是RCP 处理的结果,图中大多数伪影都被有效的去除,同时细节信息也基本得到保留.然而由于算法本身需要考虑伪影去除与细节保留之间的平衡,故一些强度较大的环形伪影还是会有些残留的痕迹.在VDM 算法的处理结果中,如图7(f)和图8(f)所示,尽管没有明显的环形伪影存在,但本该平坦的区域看起来却不够平滑.由此可见,对于实际CT 图像中环形伪影的校正,本文提出的算法也体现了更优的性能,在去除伪影的同时能更好地保持原始图像的质量.
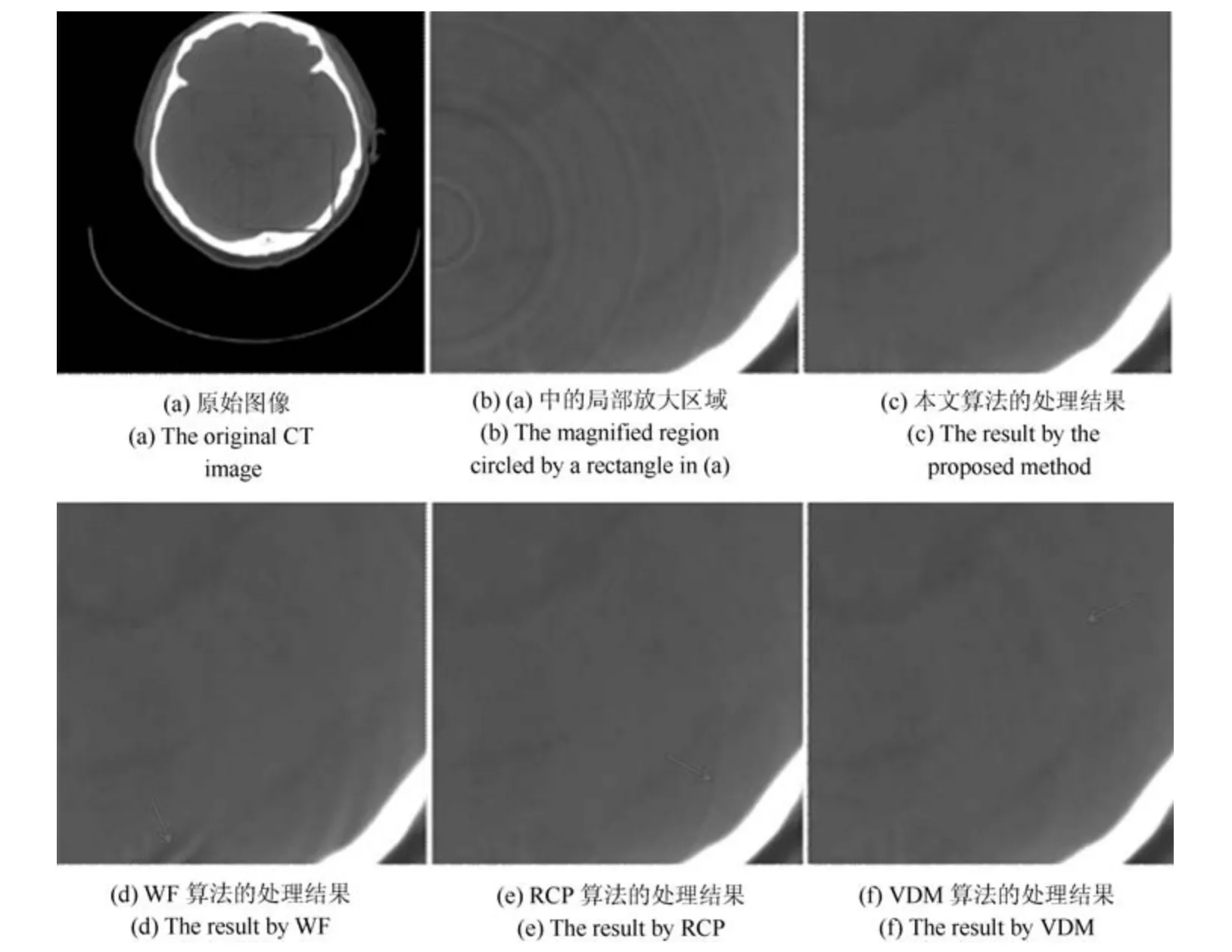
图7 脑部CT 图像处理结果Fig.7 Experiments on a brain CT image
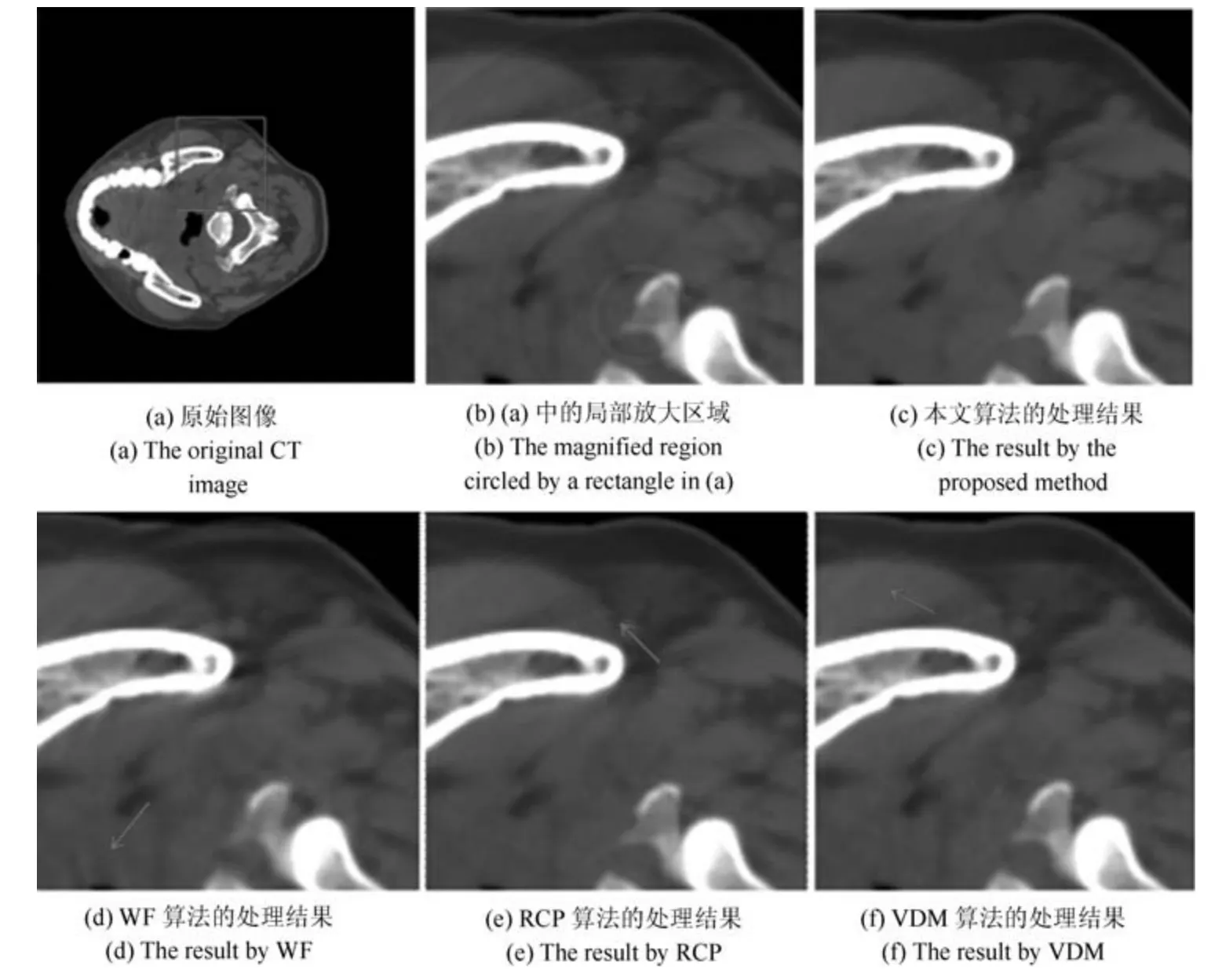
图8 颈部CT 图像处理结果Fig.8 Experiments on a neck CT image
视觉观察是检验伪影去除与图像细节保护最直接的途径,但要更精确地对比处理结果的差异,仍需客观的评价指标来进行衡量.但对于实际待处理的CT 图像,其对应的理想无伪影图像并不存在,故无法利用传统的峰值信噪比或平均结构相似性等指标来进行评价.在此我们在相对平滑的脑部CT 图像中选取几个平坦区域作为感兴趣区域(Region of interest,ROI),如图9 所示,计算这些区域的局部信噪比(Local signal-to-noise ratio,LSNR),即区域内像素值的标准差与平均值之间的比值,公式如下:
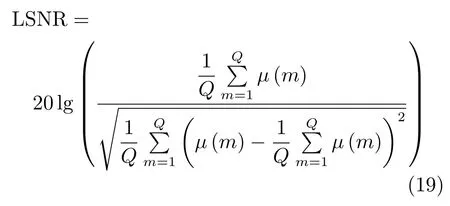
对于图像中的平坦区域,其标准差很大程度上与图像中的伪影相关,标准差的降低相应地反映了图像伪影的减少[16].显然对于处理后的图像,其平坦区域的LSNR 值越大,表明图像伪影的去除效果越好.对应图9 各方框标识的区域位置,我们依次计算出原始图像及其各算法处理结果中相应区域的LSNR 值,如表2 所列.可以看出相对于原始图像,各种算法处理后相应区域的LSNR 值均明显变大,其中本文算法较其他算法来说更为有效.
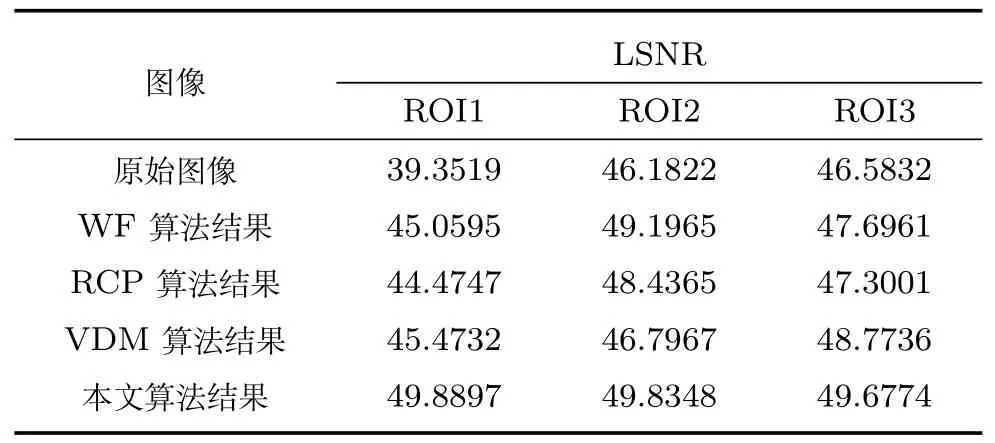
表2 各算法结果相应局部区域(图9)的LSNR 值Table 2 LSNRs of the ROIs circled in Fig.9 for different methods
3.3 实现分析
3.3.1 梯度保真与传统灰度保真的效果对比
为了单独说明校正模型中的保真项采用梯度保真形式在去除伪影时会产生更好的效果,我们以添加了伪影的Lena 图像为例,将采用梯度保真形式的模型(7)与如下采用传统灰度保真形式的模型(20)就示例图像在极坐标系下的处理效果进行实际比较.
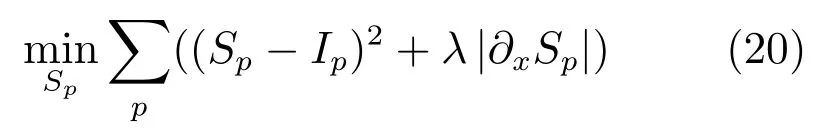
由于Lena 图像中的边缘及纹理细节信息更丰富,在此选用该图视觉上可以更明显地看出处理过程对多种图像成分的影响效果.如图10 所示,两种模型的处理均明显消除了伪影,但比较而言,使用灰度保真的模型(20)处理后的图像细节损失相对严重,且有阶梯现象出现;而使用梯度保真的模型(7),处理结果中细节信息得到了更好的保留.

图9 脑部CT 图像中的ROI 选取Fig.9 A brain CT image with ROIs
为了进一步说明模型保真项的改进在实际CT图像上的近似效果,同样在极坐标系下对比了上述两种模型(20)和(7)在包含细节信息相对较多的颈部CT 图像上的处理效果,如图11 所示.可以看出在消除了垂直伪影的同时,使用灰度保真的模型(20)处理后的图像细节损失较多;而使用梯度保真的模型(7)处理后的结果中细节信息保留较好(图中箭头所指区域的效果对比更为明显).
3.3.2 RTV 与TV 的约束效果对比
为了直观显示模型中正则项采用RTV 约束形式优于传统TV 形式的效果,我们将模型(7)与模型(8)的处理效果进行了对比,图12 为Lena 图像在极坐标系下的效果展示,显然在单向梯度保真的作用下,两者在消除垂直条状伪影的同时均较好地保留了图像中的细节信息.但仔细观察不难发现,在图像中较为显著的垂直结构边缘位置(如图12(a)中箭头所指),TV 约束模型(7)处理后其灰度和对比度均受到了一定的影响,而RTV 约束模型(8)的处理结果中看不出明显的变化.为方便观察,我们截取该位置附近的一小段水平线段(如图12(d)中的

图10 Lena 图像伪影去除效果对比Fig.10 Comparison of artifact removal effects on the Lena image
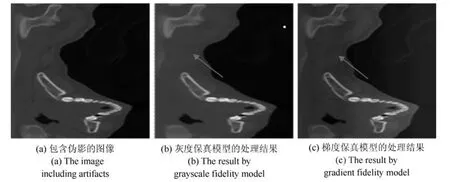
图11 颈部CT 图像伪影去除效果对比Fig.11 Comparison of artifact removal effects on the neck CT image
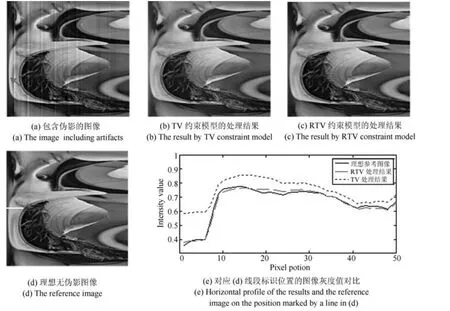
图12 Lena 图像上TV 和RTV 的约束效果对比Fig.12 Comparison of constraint effects between TV and RTV on the Lena image
线段标识),将标准原图、TV 约束模型处理结果图和RTV 约束模型处理结果图的相应位置灰度信息以曲线形式显示并加以对比,如图12(e)所示,RTV 约束模型的结果与标准原图更为接近.
同样将上述两种模型(7)与(8)作用在极坐标系下的颈部CT 图像,处理效果对比见图13,可以看出,两种模型均基于单向梯度保真,故在消除垂直条状伪影的同时均较好地保留了图像中的细节信息.但仔细对比不难发现,使用TV 约束模型(7)处理后,图像部分区域(如图12(b)中箭头所指)的灰度和对比度出现了一些变化,而使用RTV 约束模型(8)的处理结果并没有出现明显的变化.
3.3.3 RTV 与TV 的约束效果对比
式(8)中的λ作为模型的约束项系数,用来调整梯度保真程度和伪影去除程度的平衡,其值越大图像中被去除的原始信息就越多,值越小去除的信息越符合条状伪影的几何特性,可较好地保留图像原始信息.根据实际CT 图像中环形伪影的情况,λ大小通常设为1×10−4∼1×10−5较为合适,可在去除掉伪影信息的同时较好地保留图像原始信息.
式(13)中尺度参数σ用于控制相对全变分计算时涉及到的局部窗口大小.σ值的大小取决于要去除伪影的宽度,它实际上是区分图像结构性边缘和伪影边缘的尺度标准.σ值较小时,仅可去除较细的伪影,比较宽的伪影则会被作为结构性信息予以保留;σ值较大时,则可去除较宽的伪影,但同时也会影响到更多的图像结构信息.因此要根据实际伪影情况对σ的取值进行设定,通常为(0,6]范围内,在上述实验中我们设定值为3,同时在算法迭代时逐渐减小σ的值可以改善处理后的边缘轮廓清晰度,每次迭代之后执行σ ←max(σ/2,0.5).
此外式(13)中的ε值和式(14)、(15)中的εs值,这两个参数设定为较小的正数主要是为了避免公式中出现分母为0 的情况.实验中,我们设定ε值为1×10−3,εs值为2×10−2,εs设得稍微大些更有助于保留平稳变化的结构性信息.
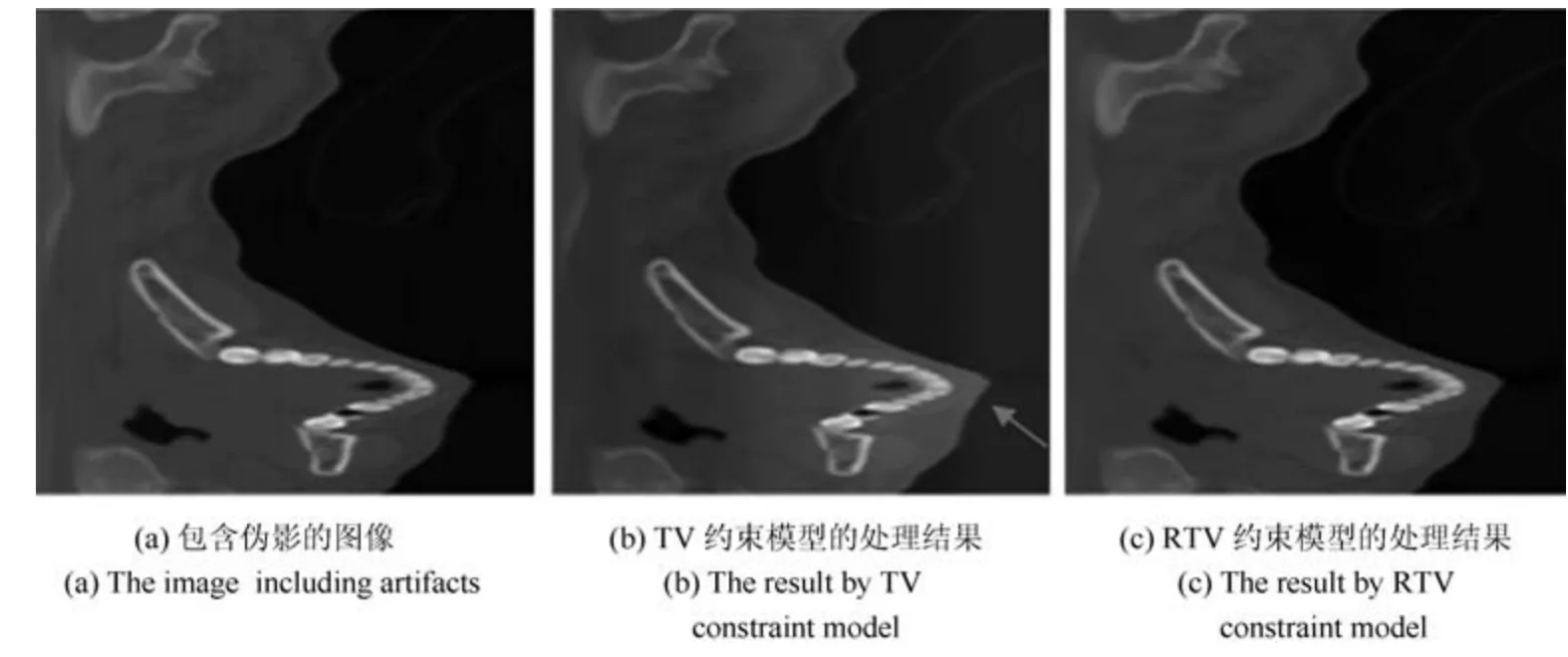
图13 颈部CT 图像上TV 和RTV 的约束效果对比Fig.13 Comparison of constraint effects between TV and RTV on neck CT image
3.3.4 算法收敛性
算法1 中在对公式迭代求解来去除图像伪影的步骤中,一般经过第一次迭代即可明显消除伪影,为了使伪影消除得更彻底,通常迭代3∼5 次足以.我们通过实验分析了该算法的收敛性,计算每次迭代后结果的归一化能量变化(Normalized step difference energy,NSDE),公式如下:
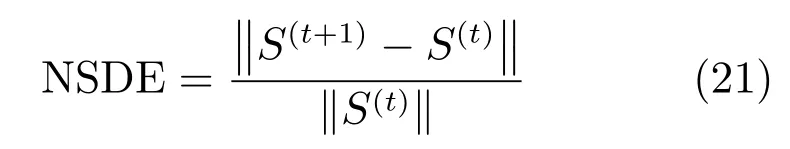
以模拟数据Lena 图像的为例,转至极坐标系下利用式(8)进行处理时,在各次迭代后计算的NSDE 值所构成的变化曲线如图14 所示.从中可以看出随着迭代次数的增加,NSDE 的值迅速下降,可见模型求解时能够快速收敛.
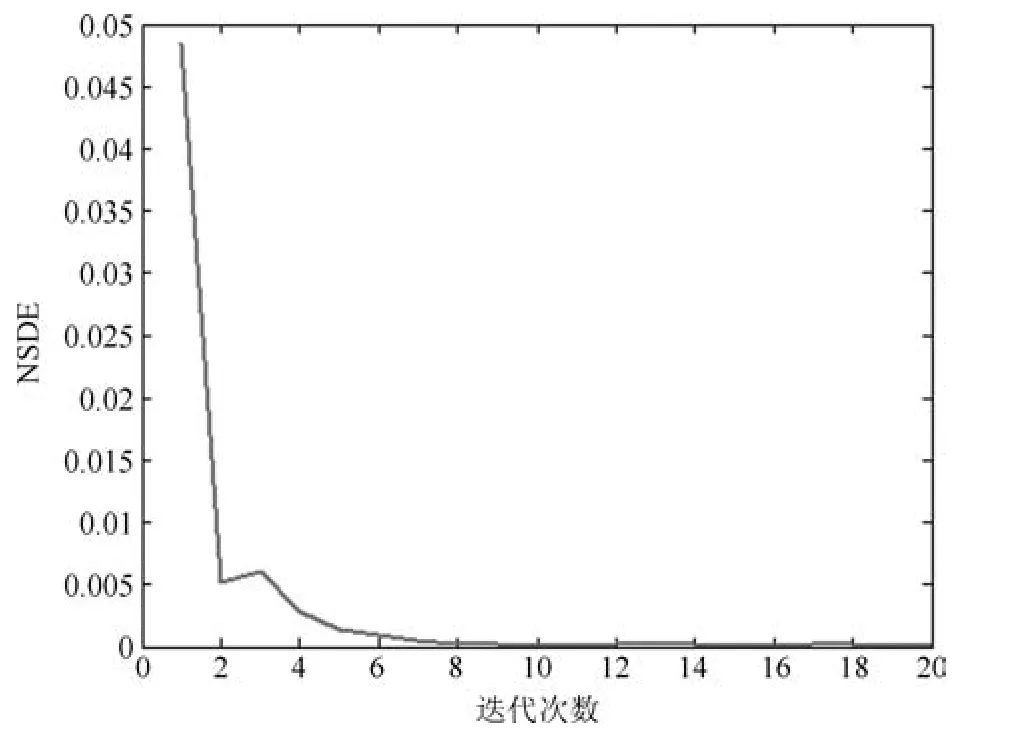
图14 算法迭代的收敛性趋势Fig.14 Convergence of iteration algorithm
4 结论
本文针对CT 图像常见的环形伪影问题,基于变分方法的思想,提出了一种作用于重建后CT 图像的校正算法来有效地去除环形伪影.构造校正模型时,结合医学CT 图像环形伪影的几何特性及边缘特性,引入了梯度保真形式和相对全变分约束形式,从而提高了对图像信息的保真性,增强了对伪影抑制的针对性.同时通过有效的优化求解,保证了校正算法的准确性和实用性.实验验证本文算法无论在模拟数据图像还是真实的CT 图像上均展示了较好的校正性能.后续研究工作中,我们将考虑校正更多的噪声成分,在现有模型基础上继续完善,不断提高校正算法的实用性.

