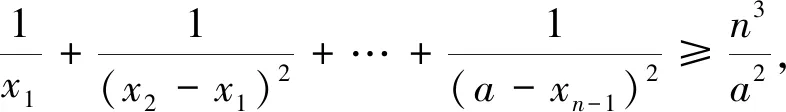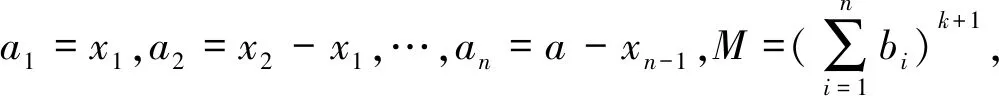一道竞赛填空题的一题多解与拓展

新疆实验中学 (830049) 晏 鸿

高中数学教学内容多，学生天天在做题，老师天天在讲题，好像数学题永远做不完，那么有没有一种行之有效的学习方法？如果现在还没有，不妨尝试一下一题多解.可能有人会认为，追求一题多解，会加重负担.本人认为不尽然，因为一题多解是用多种方法解决同一道问题，在解决问题的同时复习巩固多项数学基础知识，熟练多项解题技能，积累各种解题经验.实际上就是跳出题海，通过有限的训练达到掌握多种方法的目的.本文以一道新疆初赛填空题为例说明.

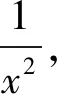
思路2：在考虑选用代数方法解决问题时，三角代换也是常用的方法，直接代换不行，但观察不等式发现分母有x,a-x，就可以考虑给它倒过来相加，再除以a就可以得到常数1，顺利引进正余弦平方和公式，把整个问题转化为三角方面的运算，这种想法的关键在于要有转化思想.

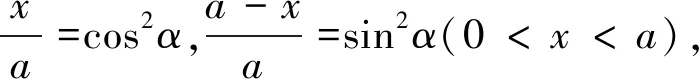
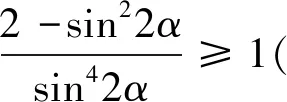
图1

思路4：前面的几种想法本质都是在转化，那能不能直接用不等式解决这个问题?由于是竞赛题，可以考虑选用常规的结论“平方平均值大于等于调和平均值”来入手.

评注:以上四种解法，基本上选用的是解决高考题的常规方法，在日常的学习过程中，需要学生夯实基础，熟练技巧，理解方法的本质、功能，增强解题思维能力，培养学习数学的兴趣，提高学习实效性.

思路5：一般情况下，竞赛题用解决高考题的常规方法去做会比较麻烦，但如果选用解决竞赛题的非常规思路去想，用均值不等式，柯西不等式以及柯西不等式的变形来做，就方便多了.

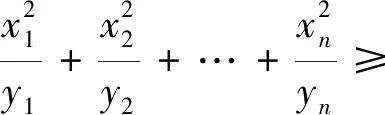
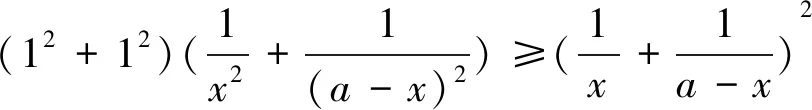
思路6：把解法5的不等式(*)进行变形，把分子处理掉，变成更简洁的形式，与题目条件直接对接，立马解决问题.只要继续往下做，就可以发现这种想法是可行的.

评注:后两种解法，选用的是非常规方法，优点是解题速度快，缺点是需要记住的中间结论多，很难想到,因此在平常的学习过程中，不要过分强调哪一种方法的重要性，而是要理解题意，分析条件，因题施策，出奇制胜，提高练习的实战性.六种解法各有特点，都值得仔细研究.

此题可作如下推广：

推广1 若0

总之，本题在具体的课堂教学过程中，学生们反应热烈，课堂气氛活跃，大多数同学都能提出自己的想法，因此老师有意识，有目的的进行了引导，诱发学生的内在动力，激发他们的探索求知欲望，使他们精神饱满，心情舒畅地渐入“解题境界”.仁者见仁，智者见智.一题多解主要是让学生学会从不同角度、不同侧面去思考问题,培养良好的思维品质,拓展解题空间，是让学生跳出题海的一件法宝.