“倒序相加法”简解一类绝对值函数最值问题

江苏省徐州市侯集高级中学 (221121) 李培颖

绝对值函数的最值问题历来是高考、自主招生、竞赛常涉及到的问题.笔者在今年高三二轮复习中针对绝对值函数最值问题进行了专题复习，讲解了一类绝对值函数的最值问题.其中2011年北大自主招生第7题(压轴题)最为典型，现在将这道试题的解法及分析与大家共赏.

题目(2011年北大自主招生第7题)求|x-1|+|2x-1|+|3x-1|+…+|2011x-1|的最小值.

本题涉及的是传统的绝对值函数的最值问题，学生最初接触到的是求解两个或三个绝对值相加的函数最值，最常用的方法是找零点(使绝对值为0的变量的值)分区间分类讨论法.即通过分类讨论将绝对值这一“面纱”揭开，将函数化为一个分段函数，逐段求解最小值，然后进行比较得出函数的最小值，这种方法我们称之为“零点分段法”.此题是一个典型的“年代题”，含有2011个绝对值，仅仅是绝对值个数的增加，显然可以使用“零点分段法”，下面是这种方法的求解过程.

解法一：令f(x)=|x-1|+|2x-1|+|3x-1|+…+|2011x-1|.

-1-2-3-…-2010+2011;

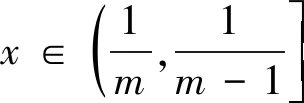
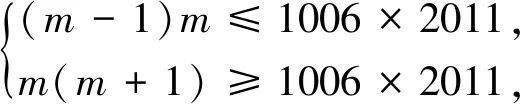
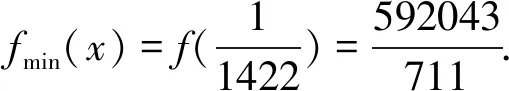
我们知道，求解绝对值函数y=|x-a|+|x-b|的最小值问题，除了使用“零点分段法”，还可以利用绝对值的几何意义求解.由|x-a|+|x-b|表示数轴上的点(x,0)到点(a,0)、(b,0)的距离之和，其最小值为|a-b|，当ab)时，在x∈[a,b]([b,a])时取得；当a=b时，在x=a=b时取得.利用这种方法求解显然比“零点分段法”简洁的多.但问题是|x-1|+|2x-1|+|3x-1|+…+|2011x-1|中x的系数不都是1，无法使用几何意义求解，接下来该怎么办呢？其实将函数f(x)的表达式进行适当变形，就可以使复杂的问题柳暗花明.

解法二:令f(x)=|x-1|+|2x-1|+|3x-1|+…+|2011x-1|，将其变形为

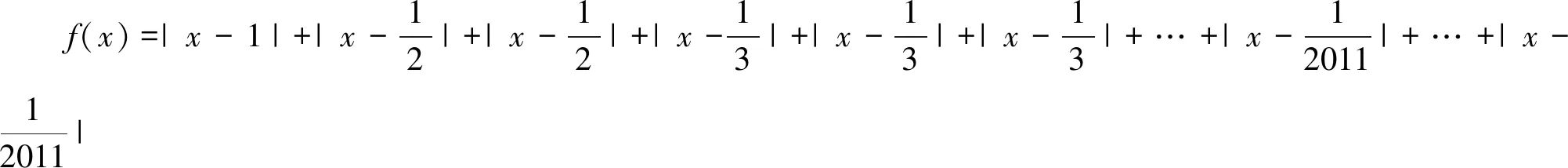
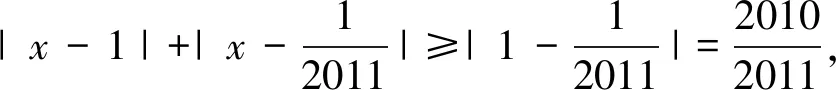
点评：“零点分段法”一般先讨论去绝对值，再利用函数的单调性等知识，以及数形结合思想、分类与整合思想和转化与化归思想解题，是解决绝对值函数的常规方法.但面对本题这种绝对值个数较多时，过程明显比较繁琐.解法二则是对函数解析式进行适当改造，巧妙地利用绝对值的几何意义，使问题轻松获解.这种方法形式上类似于等差数列前n项和的推导方法，笔者称之为“倒序相加法”.高考中，类似的问题曾经出现，比如2014年高考安徽卷(理科)第9题：若函数f(x)=|x+1|+|2x+a|的最小值为3，则实数a的值为( ).(选项略去)“零点分段法”可以求解，但“倒序相加法”要简单很多，几乎达到了“秒杀”.再比如此类问题也受到了数学竞赛命题者的青睐.2009年全国中学生数理化解题技能竞赛高二数学决赛第12题与以上两题一脉相承.原题如下：已知函数f(x)=|x+9|+|x+8|+|x+7|+…+|x-29|+|x-30|，若存在实数m，使得不等式f(x)>388+|m2-15|对于∀x∈R恒成立，求实数m的取值范围.使用“倒序相加法”亦可以使问题轻松破解.