2019年高考全国I卷不等式选讲试题分析及备考建议

广东省华南师范大学附属中学(510631) 林 琪

广东省惠州市教育科学研究院(516001) 廖伟君

1.试题呈现

题目(2019年高考全国I卷文理第23题)已知a,b,c 为正数，且满足abc=1.证明：

本题主要考查利用二元基本不等式、三元基本不等式证明不等式，也可以运用柯西不等式、排序不等式等知识解题，解答涉及根式与幂的运算，同时体现了转化与化归的思想方法.

2.解法研究

2.1.主要解法及点评

2.1.1.第一问主要解法

解法1因为a2+b2≥2ab,b2+c2≥2bc,c2+a2≥2ac，又abc=1，故有a2+b2+c2≥ab+bc+ca=所以≤a2+b2+c2(当且仅当a=b=c=1 时等号成立).

解法2因为a,b,c 为正数且abc=1，故有

所以

解法3(柯西不等式)因为a,b,c 为正数且abc = 1，故有

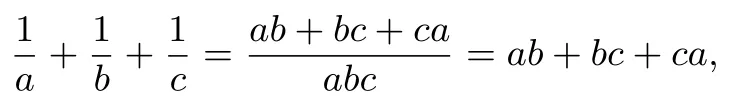
因为a,b,c 为正数且abc=1 及柯西不等式，故有

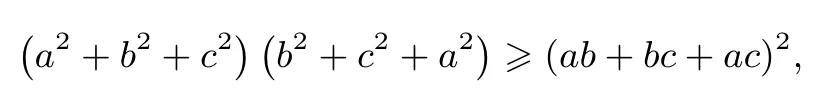
所以a2+b2+c2≥ab+bc+ac，所以a2+b2+c2≥所以≤a2+b2+c2(当且仅当a=b=c=1 时等号成立).

解法4(排序不等式)因为a,b,c 为正数且abc = 1，故有

对于两组数a,b,c 和a,b,c，不妨设a ≥b ≥c ＞0，则a2+b2+c2为其顺序和，bc+ca+ab 为其乱序和，所以a2+b2+c2≥ab+bc+ca，所以≤a2+b2+c2(当且仅当a=b=c=1 时等号成立).

点评这4 种解法的关键在于证明不等式a2+b2+c2≥ab+bc+ca，证明过程中涉及二元基本不等式、柯西不等式、排序不等式、完全平方的非负性等相关知识.

2.1.2.第二问主要解法

解法1因为a,b,c 为正数且abc=1，故有

所以(a + b)3+ (b + c)3+ (c + a)3≥ 24 (当且仅当a=b=c=1 时等号成立).

解法2因为a,b,c 为正数且abc=1，故有

所以(a+b)3+(b+c)3+(c+a)3≥24(当且仅当a=b=c=1时等号成立).

解法3因为a,b,c 为正数且abc=1，故有

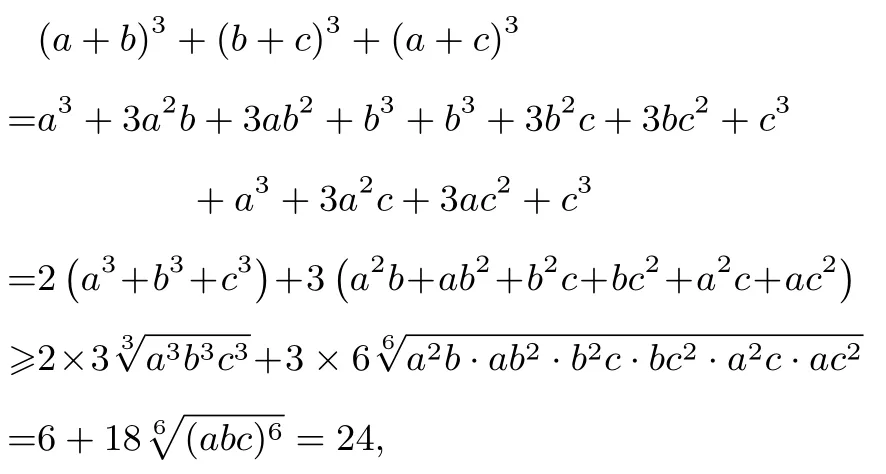
所以(a + b)3+ (b + c)3+ (c + a)3≥ 24 (当且仅当a=b=c=1 时等号成立).

解法4因为a,b,c 为正数且abc=1，故有

所以(a + b)3+ (b + c)3+ (c + a)3≥ 24 (当且仅当a=b=c=1 时等号成立).

解法5因为a,b,c 为正数且abc=1，故有

所以(a+b)3+(b+c)3+(a+c)3+8×6 ≥24(a+b+c)≥所以(a+b)3+(b+c)3+(c+a)3≥24(当且仅当a=b=c=1 时等号成立).

解法6因为a,b,c 为正数且abc = 1 及幂平均不等式，故有

所以(a+b)3+(b+c)3+(c+a)3≥3×23= 24，所以(a+b)3+(b+c)3+(c+a)3≥24(当且仅当a=b=c=1时等号成立).

解法7因为a,b,c 为正数且abc=1 及赫尔德(HÖlder)不等式，故有

所以(a + b)3+ (b + c)3+ (c + a)3≥ 24 (当且仅当a=b=c=1 时等号成立).

点评本题广东文科考生的解法相对比较单一，大多是直接先利用二元基本不等式，再用三元基本不等式处理；而理科考生的思路较为开阔，解法相对更多样化，除了利用基本不等式，还有利用幂平均不等式，但较多的学生选择将原不等式的(a+b)3+(b+c)3+(a+c)3展开，利用不同的组合方式使用基本不等式从而得证.

2.2.典型错误及分析

2.2.1.运算出错

第一问通分整理，出现

等错误.在利用分析法或作差法证明不等式时移项出错，如：

要证2bc+2ac+2ab ≤2a2+2b2+2c2，

即证(a+b)2+(a+c)2+(b+c)2≥0.

2.2.2.二元或三元或n 元基本不等式出错

本题最为关键的是利用基本不等式证明，部分考生对基本不等式的结构及其成立的条件掌握不到位，导致证明难以进行下去或出现错误.

使用二元基本不等式出现缺少系数或根号等错 误，如ab ≤ a2+ b2，ab ≤ab + bc + ac ≤等.使用三元或n 元基本不等式时，出现了与二元基本不等式的形式混淆，缺少或写错指数、根指数、系数等，如

等.

在使用基本不等式时，考生对“一正二定三相等”不是特别理解，出现了如下的错误：

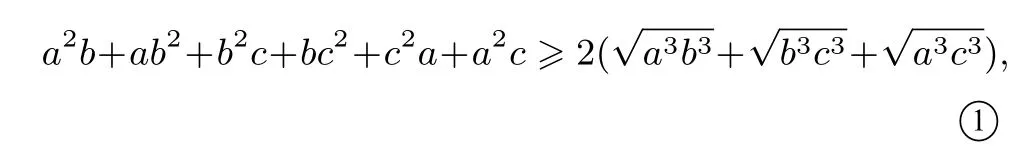
当且仅当a = b = c = 1 取等号，所以a2b + ab2+b2c + bc2+ c2a + a2c = 6.在这里，“当且仅当a =b = c = 1 取等号”指的是不等式 ①中的等号成立，即而不是说a2b+ab2+b2c+bc2+c2a+a2c=6.

在多元的基本不等式，也存在类似这样的问题，比如有考生将原不等式的左边展开并利用基本不等式：

2(a3+b3+c3)+3(a2b+ab2+b2c+bc2+a2c+ac2)≥

在这里，学生并没有真正计算根式的值，而且该等号不成立.

2.2.3.运用柯西不等式或赫尔德(HÖlder)不等式出错

定理设aij(i = 1,2,···n,j = 1,2,···m)是正实数，αj(j = 1,2,··· ,m)是正实数，且α1+α2+···+αm= 1，则

推论(赫尔德(HÖlder)不等式)：设xi＞0，yi＞0，zi＞0(i=1,2,3)，则有

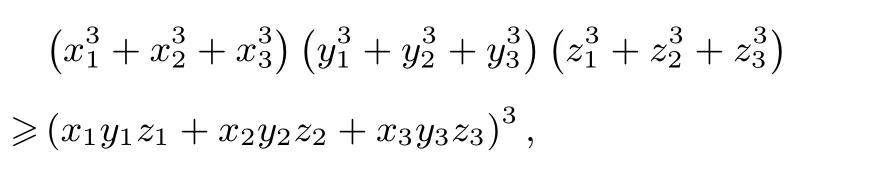
当m = 2 时，不等式便是著名的柯西不等式，这说明赫尔德不等式本质上是柯西不等式的一种推广.

柯西不等式在选修4-5《不等式选讲》中出现，部分考生对其形式不太理解，出现了

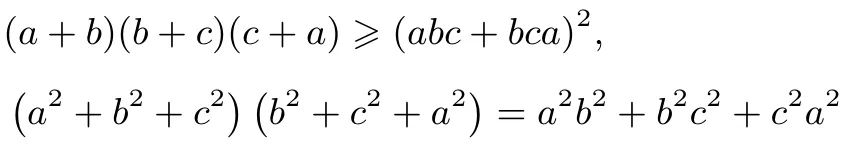
等错误形式.也有考生写出

从这个式子来看，考生大致有两种可能的错误原因，一是误以为是可直接利用柯西不等式，二是将赫尔德不等式的形式记错成如上的形式，少了一个因式13+13+13.

2.2.4.错误的推理导致出错

个别考生对多变量的问题较陌生，不能很好理解abc = 1 这个条件，甚至推导得出a = b = c = 1，或者a ＜1,b ＜1,c ＜1 等错误结论.有些考生证明中发现可由基本不等式得到如下两个不等式并错误地使用不等式的传递性得出

2.2.5.用特例验证不等式的等号或不等号成立

部分考生因对不等式证明不知如何处理或知识本身的不足，在处理本题时，运用了特例验证不等式的等号或不等号成立.如当a=b=c=1 时，如当时，

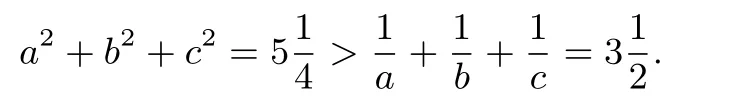
3.备考建议

3.1.考法研究

下表是近四年全国课标卷“不等式选讲”的考点分布表：

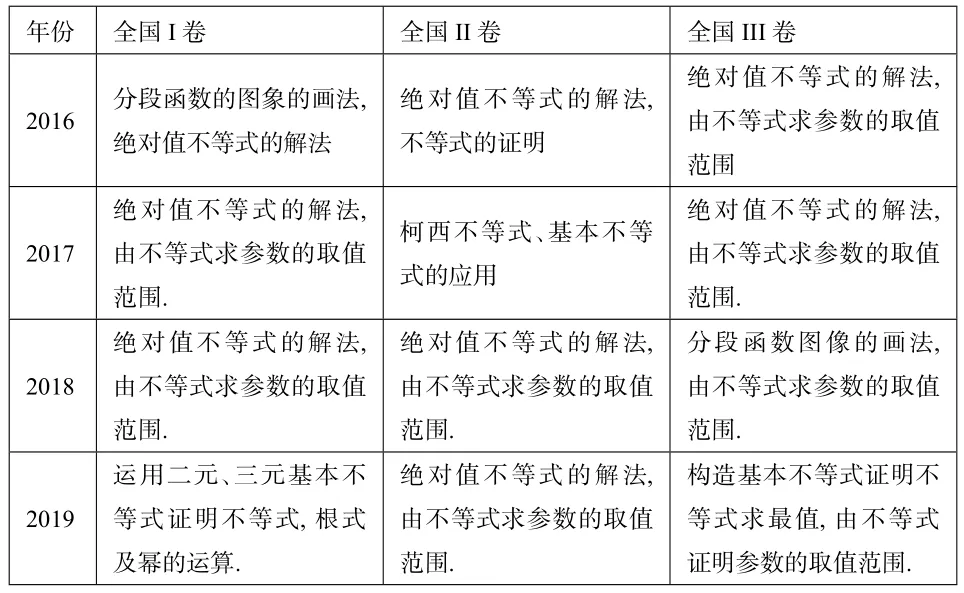
年份全国I卷全国II卷全国III卷_____________2016分段函数的图象的画法，绝对值不等式的解法绝对值不等式的解法，不等式的证明绝对值不等式的解法，由不等式求参数的取值范围__________________2017绝对值不等式的解法，由不等式求参数的取值________范围.柯西不等式、基本不等式的应用绝对值不等式的解法，由不等式求参数的取值范围._________________2018绝对值不等式的解法，由不等式求参数的取值_______________________________________范围.绝对值不等式的解法，由不等式求参数的取值范围.___________________分段函数图像的画法，由不等式求参数的取值范围.__________________2019运用二元、三元基本不等式证明不等式，根式____________________________________及幂的运算.绝对值不等式的解法，由不等式求参数的取值范围.___________________构造基本不等式证明不等式求最值，由不等式证明参数的取值范围.____

从上表中可以看出，近四年“不等式选讲”在全国卷中的考法在内容上是稳中有变.大部分以考查绝对值不等式为主，也穿插考查基本不等式或柯西不等式的运用.

3.2.教学建议

3.2.1.立足基础，关注公式教学，注重知识生成

2019年全国I卷23题不等式的考查方式与前几年有一些变化，从考查绝对值不等式的解法及不等式恒成立问题求参数范围，转变为证明不等式.这一风格的转变让许多考生不大适应，由于在复习和备考过程中，他们以绝对值函数或绝对值不等式为主要复习训练内容，忽视对基本不等式、柯西不等式等内容的复习和训练，因此造成本题广东考生得分较低.

从评卷的情况可以发现，考生们在解答过程中出现频数较多的公式错误，同时他们对二元基本不等式掌握得更为熟练，而对三元基本不等式却未能识别其结构.部分考生在面对(a + b)3+ (b + c)3+ (a + c)3时，并未能将(a+b)3,(b+c)3,(a+c)3看成整体，利用三元基本不等式求解，导致后续解答更复杂.

因此，教师在初授公式课时，尽量避免呈现式的教学方式，应更关注公式的生成，更多地采取生成式、探究式的教学方式，关注类似公式之间的区别与联系，并可以让学生发挥自己的创造力，从有限的式子拓展一些变形，促进学生对新知的认识.这样的教学方式看似占用了更多的教学时间，但能从多维度提升学生对公式的理解，加强新旧知识的关联，形成螺旋式的结构.当面对陌生的问题时，学生的思维能拥有更多的发散性和创造性.

2019年全国I卷23题的第(1)问的关键步骤“a2+b2+c2≥ab+bc+ca”与教材选修4-5 第10 页习题1-1 第7题“求证a2+b2+c2+d2≥ab+bc+cd+da”如出一辙，教材第11题“已知a,b,c ∈R+，a+b+c=1，求证也与本题类似.

无独有偶，2013年高考全国II卷理科第24题与本题类似，只是条件从abc=1 变成a+b+c=1：

题目(2013年高考全国II卷理科第24题)设a,b,c 均为正数，且a+b+c=1，证明：

我们高三的复习工作要紧扣教材、变式教学、抓纲务本，由重结论转化为重过程以及重能力培养等要落实在教学活动中.高考题源自于课本，而高于课本，在平常利用教材教学时，需要我们教师更多地挖掘教材，多角度多维度地思考课本素材的应用.

3.2.2.思考关联，关注长远发展，注重能力提升

从近几年的全国卷可以发现，试题突出学科素养导向，重点考查基础知识的运用和思维方法的掌握，增强综合性和应用性，突出对创新应用能力的考查.尤其今年高考数学全国卷设置的情境真实、贴近生活，体现数学知识和方法在解决问题中的价值和作用，同时对主观题考查内容的位置安排进行了调整，难度也有相应变化.这种设计有助于学生全面学习掌握重点知识和重点内容，同时有助于破解僵化的应试教育.从长远来看，我们要培养的是更多具有创新性的人才，而非只会简单地套用知识的学生.

结合这样的变化，作为教师的我们应思考中学教学的导向应是指向哪里?

首先，我们应该做到不随意删减教学内容.广东省2019年只有11.37% 的考生选择做23题，2018年则是12.50%，2017年更是低至9.00%.这与考生对不等式证明这部分的内容不够重视有关，考生本身对不等式证明的接受能力较弱，平常考试只选做22题，极少做23题，而且只保留解绝对值不等式的经验，面对基本不等式等问题则基本束手无策.部分学校甚至没有开设《不等式选讲》这门课程，短期来看删减了部分学习内容，提高了学生的精力付出，节省了教学及复习时间.但从长远来看，这门课程中涉及的知识对于提升学生的思维层次有很大帮助，能促使他们更灵活更全面地思考问题.另外不等式的相关问题与大学数学数学分析的知识联系紧密.缺少这部分知识，对于学生长期发展来说是相当不利的.

其次，多挖掘一些创新性情景，为学生创造解决真实问题的机会.《普通高中数学课程标准(2017年版)》突出函数、几何与代数、概率与统计、建模与探究四条主线，体现了社会发展的时代性.在教学的过程中，我们更应突出主线的教学，加强重要模型的构建，探索建模与探究的实践.数学模型搭建了数学与外部世界联系的桥梁，是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段，也是推动数学发展的动力.

最后，虽然当前的选考题型将在2020年最后一次出现在高考数学中，但作为教师必须积极负责地站好最后一班岗，毕竟绝大多数学生的高考只有一次.教学必须以学生为主体，严格按照课程标准和考试大纲的要求，把选择的权利还给学生.学生在面对多种选择能自主做出正确的判断，这需要学生有独立思考和风险决策能力，这正是学生核心素养中自主发展的一种体现.尊重学生认知发展规律，引导学生面对挑战独立决策，这正是教学过程中立德树人的一种体现.