2019年高考全国I卷解析几何试题评析及备考建议*

广东省茂名市第一中学(525000) 全 茂

2019年全国高考数学I卷的解析几何题仍然由客观题和主观题两部分组成，其中理科卷客观题以椭圆、双曲线为考点，重点考察考生的解题基本功，方法可圈可点；理科的主观题以抛物线为考点，难度有所下降.文科客观题延续一贯考法，但关于圆锥曲线的主观题出人意料的放在第21题的压轴题位置(2卷理科也是圆锥曲线试题作为压轴题)，改变了往年的由导数题作为压轴题的试卷布局，这种题序上的重大变动，对考生形成了一定的心理压力，以至于有人认为它比理科圆锥曲线的主观题还难.但如能结合圆和抛物线的定义和基本性质对问题加以转化，则可以认为整个解题过程还是较为常规的，它延续了全国卷的重本质、重通性通法、淡化解题技巧的命题风格.

以下就通过分析2019年高考的解析几何试题，总结近年来全国卷的解析几何命题特点，明确备考方向，提出备考建议.

一、2019年全国I卷理科解析几何试题解答与评析

题目1(理10 文12.)已知椭圆C 的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C 交于A,B 两点.若|AF2| =2|F2B|，|AB|=|BF|，则C 的方程为( )

分析题设条件以焦点三角形和焦点弦为背景，应充分利用椭圆定义和解三角形等有关知识求解，这是解此类问题的通性通法.

思路由已知可设|F2B| = n，则|AF2| = 2n,|BF1| =|AB| = 3n，由椭圆的定义有2a = |BF1|+|BF2| = 4n，所以|AF1|=2a-|AF2|=2n.故A 为短轴顶点，不妨设为上顶点.接下来有：

解法1由|AF2| = 2|F2B|，利用向量或相似三角形的性质得点代入椭圆方程得a2= 3，所以b2= a2-c2=3-1=2，选B.

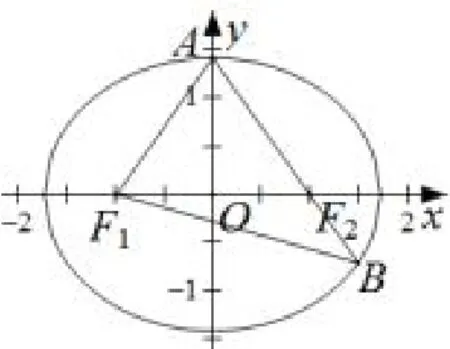
图1

解法2在△AF1B 中，由余弦定理易得cos ∠F1AB =在△AF1F2中，由余弦定理得-4n2+4n2-2·2n·2n·=4，得所以2a = 4n =所以a =所以b2=a2-c2=3-1=2，所以选B.

解法3 在 △AF1F2和 △BF1F2中，由余弦定理得又由 于∠AF2F1和∠BF2F1互补，所 以cos ∠AF2F1+cos ∠BF2F1= 0，两式消去余弦得3n2+ 6 = 11n2，解得所以2a = 4n =所以a =所以b2=a2-c2=3-1=2，所以选B.

解法4由椭圆的极坐标方程得得在ΔBF1F2中，由余弦定理得即4n2= 3 = a2，选B.

点评本题考查椭圆的标准方程及其简单性质，考查数形结合和转化化归的思想、分析问题和解决问题的能力，很好的落实了直观想象、逻辑推理等数学素养.学生首先要根据椭圆定义列出方程，得到A 点的特殊位置；再根据图形的特殊性解题，如解法1 利用共线向量坐标运算或者用相似三角形确定B 的坐标，再由方程思想迅速求解.若没有关注到特殊图形，还可用余弦定理，借助同角或互为补角的余弦关系列方程求解，如解法2 在两个三角形中对同一个角A 运算(也可对角B)，体现了算两次的思想方法；解法3 在两个三角形中对互补的两个角运算，巧妙消去余弦，充满了整体与对称的美感.解法4 则高屋建瓴，运用极坐标方程处理焦半径，颇有牛刀杀鸡的意味，供学有余力的学生参考.

焦点三角形一直是高考热点，本题题源丰富，不一而足：

题源1(2009年全国II卷理科第11题)已知双曲线= 1(a ＞0, b ＞0)的右焦点为F 且斜率为的直线交C 于A、B 两点，若则C 的离心率为( )

题源2(2010年全国II卷理12)已知椭圆1(a ＞b ＞0)的离心率为过右焦点F 且斜率为k(k ＞0)的直线与C 相交于A、B 两点.若则k =( )

题源3(2010年全国I卷理16)已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于点D，且则C 的离心率为____.

题源4(2014年安徽-14)设F1,F2分别是椭圆= 1(0 ＜b ＜1)的左、右焦点，过点F1的直线交椭圆E 于A,B 两点，若|AF1|=3|BF1|，AF2⊥x 轴，则椭圆E 的方程为____.

题目2(理16)已知双曲线C :=1(a ＞0,b ＞0)的左、右焦点分别为F1,F2，过F1的直线与C 的两条渐近线分别交于A,B 两点.若则C的离心率为____.

分析本题结合平面向量考查双曲线的渐近线和离心率.离心率的计算，关键是利用题设条件构建关于a，b，c 的一个等式关系，解题中若恰当采取几何法则较为简捷.

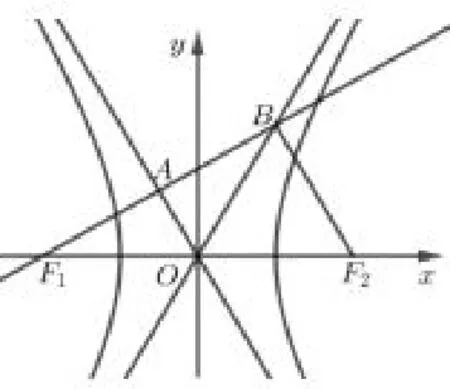
图2

解法1如图，由得F1A = AB.又OF1= OF2，得OA 是三角形F1F2B 的中位线，即BF2//OA，BF2= 2OA.由得F1B⊥F2B，所 以OB = OF1，∠AOB =∠AOF1，又OA 与OB 都 是 渐 近 线，所 以∠BOF2=∠AOF1.又∠BOF2+ ∠AOB + ∠AOF1= π，所 以∠BOF2= ∠AOF1= ∠BOA = 60°，又渐近线OB 的斜率为

解法2注意到OB = OF1= OF2= c，得到OA 垂直平分F1B，则∠AOF1= ∠BOA，由渐近线OA、OB 的对称性，得则所以∠BOA = 60°，ΔOF2B 为等边三角形，所以该双曲线的离心率为

解法3据題意可知点A 为F1B 的中点，F2B⊥F2B，又点O 为F2F2的中点，可知OA//F2B,∠OAF2= 90°.设渐近线的傾斜角为θ，由双曲线焦点到渐近线的距离为b，得可知OA = a,BF2= 2a,OB =OF2= c，得△OF2B 为等边三角形，得离心率为2.或者由余弦化简即可得e=2.

解法4因为点B 在渐进线上，可设B(am,bm)，m ＞0，由得(c - am,-bm)=(a2-b2)(m2-1)= 0，得m = 1，而点A 在渐近线上，故故c=2a,e=2.

解法5由O,A 是中点，可得OA//BF1,OA⊥BF1，由双曲线焦点到渐近线的距离为b，从而AB = b,OA =由夹角公式所以

解法6如解法1 得F1B⊥F2B，所以OA⊥F1A，从而kF1BkOB= kF1B(-kOA)= 1，因此由于与渐近线的交点为则

点评本题考查考查双曲线的几何性质(主要是渐近线与离心率)，还有平面向量数量积的相关问题，考查学生的图形理解能力和综合运用知识的能力，渗透了逻辑推理、直观想象和数学运算素养.如果考生只会用解析法解，就会出现解法6 那样的复杂运算，但如掌握好初中平面几何的相关知识，则只需用上一两个定理就能把复杂的运算问题转化为简单的推理证明，思路快捷，可谓大道至简! 以下两道题有异曲同工之妙：

2.(广东茂名2019 届高三一模理科第12题).已知双曲线=1(a ＞0,b ＞0)的左，右焦点F1,F2，右顶点为A,P 为其右支上一点，PF1与渐近线交于点Q，与渐近线交于点R，RQ 的中点为M，若RF2⊥PF1，且AM⊥PF1，则双曲线的离心率为( )

题目3(理科数学第19题)已知抛物线C : y2= 3x 的焦点为F，斜率为的直线l 与C 的交点分别为A,B，与x轴的交点为P

(1)若|AF|+|BF|=4，求l 的方程.

分析(1)设直线l : y =由抛物线定义得联立直线方程与抛物线方程，利用韦达定理可构造关于t 的方程，解方程求得结果；

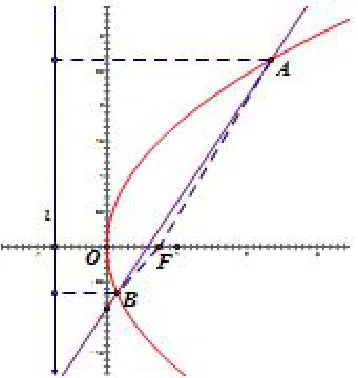
图3

解法1(1)设直线l 与x 轴交于P(m,0)，方程为得y2- 2y - 3m =0，设A(x1,y1)，B(x2,y2)，y1+ y2= 2，y1y2= -3m，Δ = 4 + 12m ＞ 0，|AF|+ |BF| = x1+ x2+=得因此直线l 的方程为即

解法2(1)设直线l 的方程为B(x2,y2)，由题设得故|AF| + |BF| = x1+由题设得由得9x2+12(t-1)x+4t2=0，则Δ=144(t-1)2-4×9×4t2=144(1-2t)＞0，x1+x2=从而得因此直线l 的方程即

(2)由(1)9x2+12(t-1)x+4t2= 0，得x1+x2=由得y1= -3y2，可得故

解法3设直线l 的方程为B(x2,y2)，由题设得故

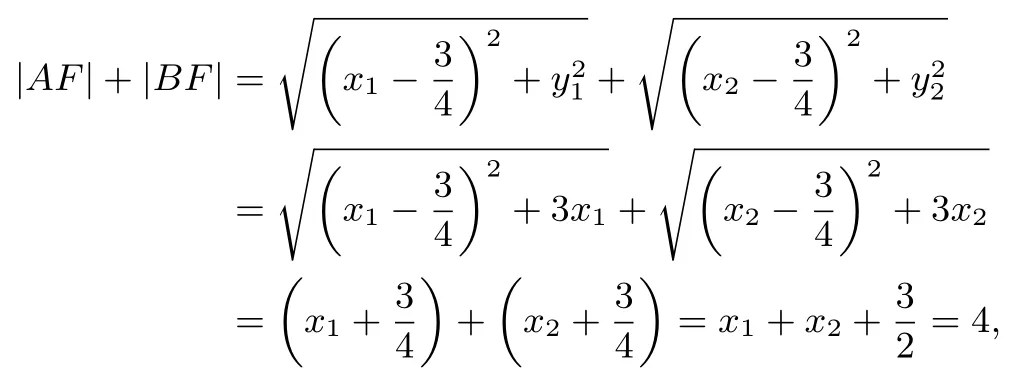
解法4设直线l 的方程为B(x2,y2)，以下略.

解法5(点差法)(1)设直线l 的方程为A(x1,y1)，B(x2,y2)，由题设得故|AF|+|BF|=由题设得由y21-y22=3x1-3x2，得所以y1+y2= 2，弦AB 的中点为而且M 在抛物线内部，因此直线l 的方程为即以下略.

解法6直线l 与x 轴的交点为P(m,0).

解法7(2)(直线的参数方程)

上述解法采用了标准形式的参数方程，运算量稍大，可改成下面一般形式来求解，更加简捷：

点评本题考查抛物线的几何性质、直线与抛物线的综合应用问题，涉及到平面向量、弦长公式的应用，满分学生相对往年多，由此可见理科的圆锥曲线大题有降低难度、减少运算量的趋势.解题的第一个关键是能通过直线与抛物线方程的联立，通过韦达定理构造等量关系；第二个关键是要善用转化与化归思想：用抛物线的定义转化|AF|+|BF| = 4，用相似三角形或线性运算破译本题的第一问来自于教材，稍高于教材，也算是2018年全国二卷圆锥曲线大题的改编题，第二问是个常规题型，在椭圆、双曲线及抛物线都出过很多类型题：

题源1(2018年全国I卷理科第8题)设抛物线c : y3= 4x 的焦点为F，过点(-2,0)且斜率为的直线与C 交于M,N 两点，则

A.5 B.6 C.7 D.8

题源2(2018年全国II卷理科)设抛物线C : y2= 4x的焦点为F，过F 且斜率为k(k ＞0)的直线l 与C 交于A,B 两点，|AB|=8.

(1)求l 的方程；

(2)求过点A,B 且与C 的准线相切的圆的方程.

二、2019年全国I卷文科解析几何试题解答与评析

题目1(文科第10题)双曲线C :=1 (a ＞ 0,b ＞ 0)的一条渐近线的倾斜角为130°，则C 的离心率为( )

A.2 sin 40°B.2 cos 40°C.2 cos 40°D.

解选D.事实上，由双曲线渐近线定义可得tan 130°，所以所以

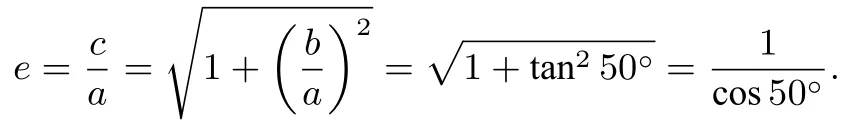
点评此题考查双曲线的渐近线的倾斜角，同时考同角三角函数的公式.分值不多，但内容不少，在重点考查基础内容与方法的同时体现了良好的覆盖面，堪称“麻雀虽小五脏俱全”.

题目2(文科第12题)即是理科第10题，对于理科生只是一道偏难的中等题，但是对文科生则属于难题，所放的位置恰到好处.

题目3(文科第21题)已知点A,B 关于原点O 对称，|AB|=4，⊙M 过点A,B 且与直线x+2=0 相切.

(1)若A 在直线x+y =0 上，求⊙M 的半径；

(2)是否存在定点P，使得当A 运动时，|MA|-|MP|为定值? 并说明理由.

分析(1)设A(t,-t)，B(-t,t)，根 据|AB| = 4 得由圆的性质可知圆心M 在直线y = x 上，可设圆心M(a,a)； 利用圆心到x+2 = 0 的距离为半径和|MA|=|MB|=r 构造方程，解出r；

图4

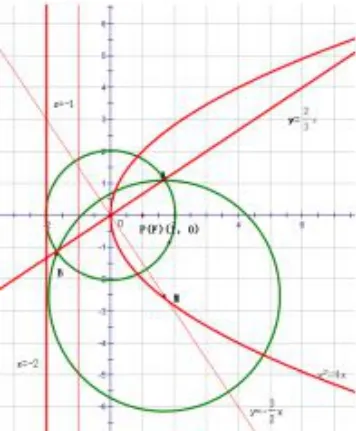
图5

(2)关键在于求出动圆圆心M 的轨迹方程.紧抓所给的几何特征，就是M 必须满足三个条件：圆心在线段AB 的垂直平分线上； 圆过点A,B； 圆与直线x = -2 相切.于是可设圆心M 的坐标，利用圆心到x+2 = 0 的距离为半径和构造方程，解出M 坐标，可知M 的轨迹为抛物线；利用抛物线定义可知为抛物线焦点，且定值为1，从而得结论.

第(1)问解法1(1)因为⊙M 经过A,B 两点，所以点M 在线段AB 的垂直平分线上.因为lAB:x+y =0 且A,B关于原点O 对称，所以M 在直线y =x 上，可设M(a,a)，因为⊙M 与直线x=-2 相切，所以⊙M 的半径为r =|a+2|，又因为AO ⊥MO，且|AO| = 2，所以(a+2)2= 2a2+4，解得a=0 或a=4，所以⊙M 的半径r =2 或r =6.

第(1)问解法2如解法1，M 在直线y = x 上，设M(a,a)，⊙M 的半径为r = |a+2|，又因为|AB| = 4，所以所以解得a = 0 或a = 4，所以⊙M 的半径r = 2 或r =6.

第(1)问解法3因为|AB|=4，且lAB:x+y =0，所以设M(a,b)，因为|MA|=|MB|，所以解得a = b.因为⊙M 与直线x = -2 相切，所以⊙M 的半径为r = |a + 2|，又因为r2= |MA|2，即(a + 2)2=以下同解法1.

第(1)问解法4因为|AB| = 4，且lAB: x+y = 0，所以设⊙M 的方程为(x-a)2+(y-b)2=r2，故得a=b.以下同解法1.

第(2)问解法1存在定点P(1,0)使得|MA|-|MP|=定值.理由如下：

设M(x,y)，由已知可得⊙M的半径r = |x + 2|，又因为r = |MA|，所以r2= |MA|2，即(x + 2)2=|MO|2+ |AO|2=(x2+y2)+ 4，化简可得y2= 4x，故点M 的轨迹是以点P(1,0)为焦点，x = -1 为准线的抛物线.因为|MA| = r = x + 2，|MP| = x + 1，故|MA|-|MP|=(x+2)-(x+1)=1.故存在定点P(1,0)，使得|MA|-|MP|为定值1.

第(2) 问解法2设M(x,y)，|OM| = t，由已知得|OA| = 2，OM ⊥ OA，可设A(2 cos θ,2 sin θ)，得M(t sin θ,-t cos θ)或M(-t sin θ,t cos θ)，作MH 垂直直线x+2 = 0 于H，则|MH| = |MA|，所以|-t sin θ +2| =或| - t sin θ +化简得t2cos2θ =±4t sin θ，即y2=4x.以下同解法1

第(2)问解法3当直线AB 的斜率存在且不为0时，设根据|OA| = 2，可 取点A 的坐标为这时 点M 在直线则r2= |xM+2|2=解得xM= 0,xM= 4k2，所以M 点的坐标为(0,0)或(4k2,-4k).当直线AB 的斜率不存在或者为0 时，点A 在x 轴或y 轴上，易得点M(0,0)，两种情况的点M 的坐标都满足y2=4x.综上所述，点M 的轨迹方程为y2=4x.以下同解法1.

第(2)问解法4设M(x,y)，由已知可得⊙M 的半径r = |x + 2|，又因为r2= |MA|2，即(x + 2)2=|MO|2+ |AO|2=(x2+y2)+ 4，化简可得y2= 4x.故|MA|=x+2，假若存在定点P(a,b)，使得|MA|-|MP|=定值m，则

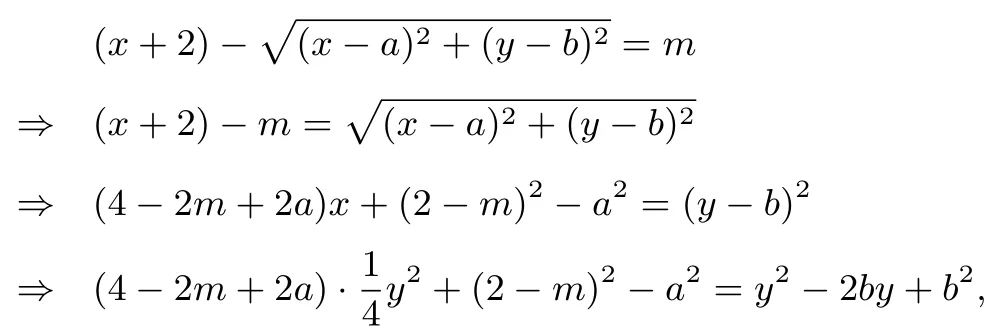
点评本题考查圆的方程的求解问题、圆锥曲线中的定点定值类问题.第一问较基础但对第二问有启示作用，第二问求解轨迹方程的入口较宽，解法多样，解题关键是根据圆的性质得到动点M 所满足的轨迹方程，点M 的轨迹方程求出后，结合抛物线的定义容易得到定值.

本题处于压轴位置，突破常规框架，考法新颖，考察学生的综合创新能力，对于文科学生而言难度较大，感觉题目比理科圆锥大题还难.第一问需要综合分析相切、点在圆上等条件，第二问打破了简单的相交-联立-韦达定理的套路，只会靠套路得步骤分的学生就会慌了阵脚.

本题第二问求点M 的轨迹方程问题，源于：

题源1(2013年陕西卷理科第20题)已知动圆过定点A(4,0)，且在y 轴上截得的弦MN 的长为8.

(1)求动圆圆心的轨迹C 的方程；

(2)已知点B(-1,0)，设不垂直于x 轴的直线与轨迹C交于不同的两点P，Q，若x 轴是∠PBQ 的角平分线，证明：直线l 过定点.

而且该题的(2)与2018年全国I卷理科19题的(2)有令人惊奇的关系：

题源2(2018年全国I卷理科19 (2))设椭圆c :的右焦点为F，过F 的直线与C 交于A,B两点，点M 的坐标为(2,0).

(1)当l 与x 轴垂直时，求直线AM 的方程；

(2)设O 为坐标原点，证明：∠OMA=∠OMB.

三、高考命题特点的领悟与分析

受篇幅限制，仅以全国I卷理科的解析几何5年考点分布为例：

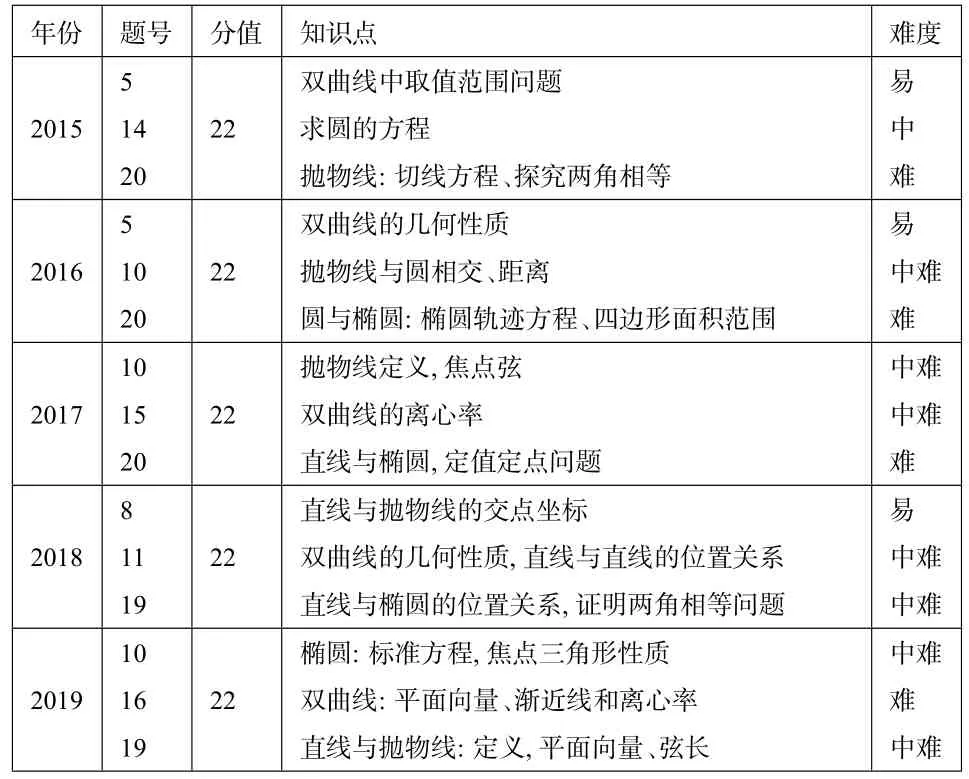
年份题号分值知识点难度5 201514____________________________20 22双曲线中取值范围问题求圆的方程抛物线：切线方程、探究两角相等_________________易 中难___5易201610____________________________20 22双曲线的几何性质抛物线与圆相交、距离圆与椭圆：椭圆轨迹方程、四边形面积范围_________中难难___2017 10 15____________________________20 22抛物线定义，焦点弦双曲线的离心率直线与椭圆，定值定点问题______________________中难中难难___8易201811____________________________19 22直线与抛物线的交点坐标双曲线的几何性质，直线与直线的位置关系直线与椭圆的位置关系，证明两角相等问题________中难中难2019 10 16____________________________19 22椭圆：标准方程，焦点三角形性质双曲线：平面向量、渐近线和离心率直线与抛物线：定义，平面向量、弦长______________中难难中难

从上表可以看到近年高考全国I卷的数学试题与高考改革所倡导的“突出独立思考、逻辑推理、数学应用、数学阅读和表达等关键能力的考查，突出对数学思想方法的理解，重视数学核心素养考查”的思想是契合的.试题呈现如下特点：

(1)题型稳定，分值不变三种题型都有，基本保持为两道选择题和两道解答题(含选考的坐标系与参数方程，本刊另有专文分析)，或一道选择题一道填空题和两道解答题，共4 道题，分值为22+10 分.选择与填空题有一道起点较低，另一道则较难或是压轴题.小题和解答题的第(1)问侧重考查圆锥曲线的定义与基本性质；解答题的第(2)问，往往有多种不同的呈现形式.

(2)整体平衡，重点突出对直线、圆、圆锥曲线知识的考查没遺漏，通过对知识重组，考查时既注意全面，更突出重点，突出了核心主干知识的价值和考查力度，保证了较高的考查比例并保持必要深度.内容主要集中在如下几个类型：

①求曲线方程(类型确定或待定)；

②直线与圆锥曲线的位置关系、弦长、面积问题；

③与曲线有关的范围、定点、定值问题；

④与曲线有关的几何证明(对称、平行、垂直)；

⑤探求曲线方程中几何量及参数间的数量特征.

(3)能力立意，渗透思想计算量减少，思考量增大，一些常见的基本题型，借助数形结合就能快速准确得到答案.解析几何与向量都具有数与形结合的特征，所以这两者多有结合，在它们的知识点交汇处命题，是高考命题的一大亮点.此外还要加大与函数、方程、不等式等相关知识的交汇联系，加大探索性题型的分量，凸现研究性学习的能力要求.

(4)难度各异，题序不定小题上，文科保持传统做法，理科则定格为中等偏难和难题；解答题位置不定，如今年I卷理科难度下降，而文科和II卷理科的解析几何大题则取代导数成为压轴，位置的变化必将影响相对难度的调整，解答题终将成为决胜高考的重要增分点，应切实引起关注.而在文理不分科命题趋势下，试题又如何设置? 引人遐思和期待!

值得注意的是：一线教师研究高考除了研究考题，还要研究《课程标准》、《考试大纲》与《考试说明》(这三者是高考命题的重要依据)，不要局限于近三年，更不要局限于I卷，应该放眼近五年文理科所有题目，广泛取材全国1、2、3卷乃至研究各省市高考题.

四、2020年高考数学解析几何备考建议

基于考生答卷中出现的一些典型错误及全国卷解析几何的命题特点，给出如下备考建议.

(1)全面复习，夯实基础，强化双基，重视总结.要牢固掌握定义，重视基础知识，基本题型的训练，各类题型都要过关，不漏一个，不搞押题活动.注意课本典型例题、习题的延伸，教材中的例题、习题虽然大多比较容易，但解法具有示范性，可延伸性，要适当编拟题组进行复习训练，融会贯通；对于热点问题，不仅要掌握方法，还要学会思考.

(2)引导学生构建好知识网络.在高中数学知识的教学中，直线和圆的方程在必修教材中，圆锥曲线安排在选修系列.在高三复习时，要打破教材排列顺序的约束，引导学生构建知识网络，对所学的知识进行梳理，以达到知识条理化、系统化的目的.

(3)重视对数学思想和方法进行归纳提炼，强化目标意识，优化解题思维，简化解题过程.在复习时要注重引导学生理解解析几何的基本思想，要求学生必须有画图、析图、用图的意识和习惯；要立足概念，返璞归真，重视挖掘图形的几何特征，减少运算量；要利用图形，巧妙转化，实现几何条件代数化.要掌握坐标法、待定系数法、建模构造法、设而不求整体运算等方法技巧，要活用数形结合、函数方程、转化化归和分类讨论等数学思想.

(4)圆锥曲线本质上属于几何的内容，要重视初中平面几何知识的应用.尽管考试大纲已经从选考模块中删去“几何证明选讲”选做题，但删去它并不代表真的会减轻平面几何的分量，反而恰恰可能在其他试题里找到一种平衡，反而要更加重视起来关注平面几何知识方法与性质在问题转化中的应用，关注几何图形相关方法在运算中的应用.从前面每一道高考题的分析和解答中，我们发现利用平面几何解决高考问题已经成为高考命题的一种趋势，适当利用平面几何知识的确可以成为解题利器.学生在初中就已经学习了平面几何的一些性质，再加上高中几何知识的补充与强化，学生有了较为全面的平面几何知识，较好的应用平面几何的能力，所以如果能够有意识地能够将平面几何的知识应用上去，结合圆锥曲线的知识进行求解，就能另辟蹊径、删繁就简，收到事半功倍、巧妙解题的效果.