2019年高考全国I卷概率与统计试题分析及备考建议

广东省华南师范大学数学科学学院(510631) 赵 萍

广东省佛山市乐从中学(528315) 林国红

一.2019年全国I卷概率与统计试题分布一览表

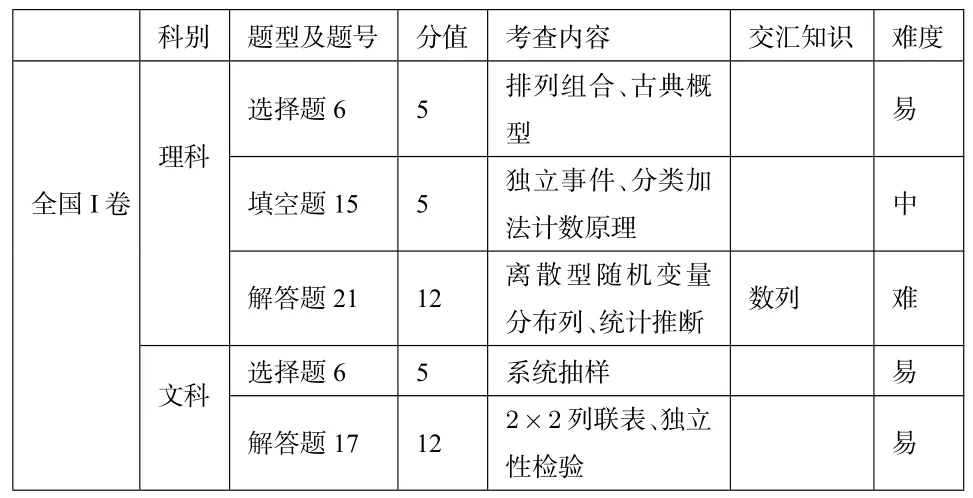
科别题型及题号分值考查内容交汇知识难度选择题6 5排列组合、古典概型易理科全国I卷填空题15 5独立事件、分类加法计数原理中解答题21 12离散型随机变量分布列、统计推断数列难文科选择题6 5系统抽样易解答题17 122×2 列联表、独立性检验易

二.2019年概率与统计试题特点分析

特点1：基础性

题目1(全国I卷文科第6题)某学校为了解1 000 名新生的身体素质，将这些学生编号为1，2，…，1 000，从这些新生中用系统抽样方法等距抽取100 名学生进行体质测验.若46 号学生被抽到，则下面4 名学生中被抽到的是( )

A.8 号学生 B.200 号学生

C.616 号学生 D.815 号学生

分析本题考查的是抽样方法中的系统抽样，理解系统抽样的特点是关键.抽取100 名学生，可分为100 组，由于组距为10，因此选出的号码所成为的数列是以10 为公差的等差数列，46 号学生被抽到，可知被抽的标号为6，16，26……，尾号都为6，故选C.

特点2：应用性

题目2(全国I卷理科第15题)甲、乙两队进行篮球决赛，采取七场四胜制(当一队赢得四场胜利时，该队获胜，决赛结束).根据前期比赛成绩，甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6，客场取胜的概率为0.5，且各场比赛结果相互独立，则甲队以4：1 获胜的概率是____.

解析本题从试题中体现体育，引入非常普及的篮球运动比赛，以普遍存在的比赛结果的预估和比赛场次的安排提出问题，考查学生应用独立事件、统计推断等数学知识、方法解决问题.欲使甲队4：1 获胜，则第五场甲胜，前四场甲胜三场负一场.可能情况为：1 负或2 负或3 负或4 负，即两主场负一场或两客场负一场，故概率为

特点3：创新性

全国I卷(理科)第21题信息量大、情景陌生，除了考查概率与统计的知识外，还综合考查等比数列的证明与数列求和等相关知识，具有较大的创新性，具体分析见文章第三部分理科21题-试题呈现与解答.

特点4：突出数学文化

题目3(全国I卷理科第6题)我国古代典籍《周易》用“卦”描述万物的变化，每一“重卦”由从下到上排列的6 个爻组成，爻分为阳爻“——”和阴爻“——”，如图就是一重卦.在所有重卦中随机取一重卦，则该重卦恰有3 个阳爻的概率是 ( )

图1

解法1从在所有重卦中随机取一重卦这句话，大部分考生会联想到此题的数学模型是古典概型，这样第一步求出基本事件的总数是26=64，恰有3 个阳爻的重卦有C36=20个，第二步用古典概型的概率公式求出答案A.

解法2从阳爻和阴爻这2 个原子概念学生很容易联想到抛硬币的正面和反面，这样可以概率统计思想及基本概念分析：阳爻“——”和阴爻“——”—随机现象—抛硬币的正面和反面，

“重卦”从下到上排列的6 个爻组成—随机过程—抛6次硬币，

“重卦”—随机事件—独立重复实验.

一个“重卦”里阳爻的个数—随机变量X —独立重复实验里事件A 发生的次随机变量X 服从二项分布不难理解求在所有重卦中随机取一重卦，则该重卦恰有3 个阳爻的概率等价于求在一个重卦里恰好有3 个阳爻的概率，就是抛6 次硬币里恰好有3 次正面的概率

三.理科21题解析

题目4(全国I卷理科第21题)为了治疗某种疾病，研制甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1 分，乙药得-1 分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分，甲药得-1 分；若都治愈或都未治愈则两种药均得0 分.甲、乙两药的治愈率分别记为α 和β，一轮试验中甲药的得分记为X.

(1)求X 的分布列；

(2)若甲药、乙药在试验开始时都赋予4 分，pi(i =0,1,···8)表示“甲药的累计得分为i时，最终认为甲药比乙药更有效”的概率，则p0= 0，p8= 1，pi=api−1+bpi+cpi+1(i = 1,2,···7)，其中a = P(X = -1)，b=P(X =0)，c=P(X =1)，假设α=0.5，β =0.8.

(i)证明：{pi+1-pi}(i=0,1,2,···7)为等比数列；

(ii)求p4，并根据p4的值解释这种试验方案的合理性.

1.试题评析

本题在具体情境中融合概率统计与数列的知识，主要考查学生的数学建模、抽象概括、数学运算、逻辑推理等数学学科核心素养，具体考查离散型随机变量的分布列、互斥事件的概率解法公式、相互独立事件的概率乘法公式、等比数列证明、递推数列求通项、求和，小概率事件的决策问题等，属于半开放的综合性试题.题目具有创新性，有很好的区分度.

2.试题解析

第(1)问解法1由题意X 可能的取值为-1,0,1，P(X =-1)=(1-a)β，P(X =0)=αβ+(1-α)(1-β)=2αβ-(α+β)+1，P(X =1)=α(1-β)，所以X 的分布列为

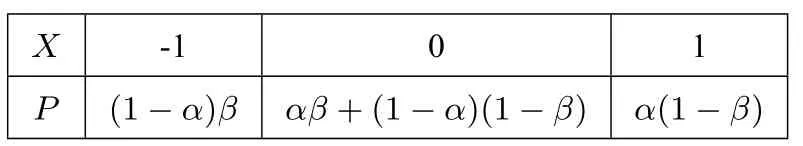
X -1 0 1_____P (1-α)β αβ+(1-α)(1-β)α(1-β)_

第(1)问解法2由题意X 可能的取值为-1,0,1，所以X 的分布列为

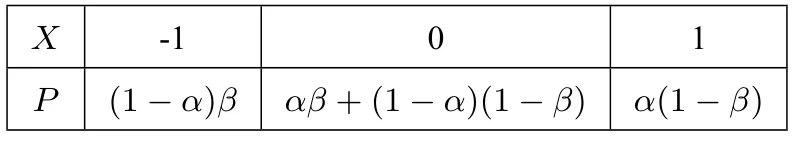
X -1 0 1____P (1-α)β αβ+(1-α)(1-β)α(1-β)_

第(1)问解法3(1)由题意X 可能的取值为-1,0,1，所以X 的分布列为

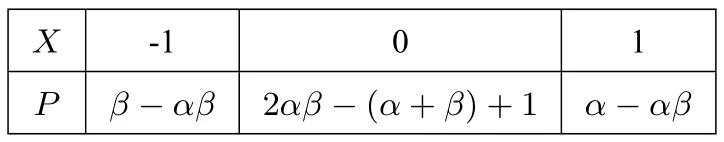
X -1 0 1____P β-αβ 2αβ-(α+β)+1 α-αβ_

第(2)问(i)解法1(i)由(1)得a = P(X = -1)=(1 - α)β = (1 - 0.5)× 0.8 = 0.4，b = P(X = 0)=αβ + (1 - α)(1 - β)= 0.5 × 0.8 + 0.5 × 0.2 = 0.5，c = P(X = 1)= α(1 - β)= 0.5 × 0.2 = 0.1，因此pi= 0.4pi−1+ 0.5pi+ 0.1pi+1，故pi+1= 5pi- 4pi−1，得pi+1- pi= 4(pi-pi−1)(j = 1,2,······ ,7).因 为p1-p0=p1/=0，所以{pi+1-pi}(i=0,1,2,……,7)是以p1为首项，4 为公比的等比数列.

第(2)问(i)解法2因为pi=a·pi−1+b·pi+c·pi+1，又因为1-b=a+c，所以(a+c)pi=a·pi−1+c·pi+1，故c·(pi+1-pi)=a·(pi-pi−1)，即因为所以{pi+1-pi}(i=0,1,2,……,7)是以p1为首项，为公比的等比数列.

第(2)问(i)解法3因为pi= (1-α)β·pi−1+(αβ-(1-α)(1-β))·pi+α(1-β)·pi+1，所以(α+β-2α·β)pi=(1-α)β·pi−1+α(1-β)·pi+1，故α(1-β)·(pi+1-pi)=(1-α)β·(pi-pi−1)，即因为p1-p0=p1/=0，所以{pi+1-pi}(i=0,1,2,……,7)是以p1为首项，为公比的等比数列.

第(2)问(ii)解法1由(i)得p8=p8-p7+p7-p6+···+p1-p0+p0=(p8-p7)+(p7-p6)+······+(p1-p0)+p0=因为p8= 1，故所以p4= (p4-p3)+(p3-p2)+(p2-p1)+(p1-p0)+p0=表示最终认为甲药更有效的概率.由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8时，认为甲药更有效的概率为此时得出错误结论的概率非常小，说明这种实验方案合理.

第(2)问(ii)解法2由(i)有pi+1- pi= p1·4i(i = 0,1,2,……,7)，累加可得p8- p0= p1·(40+41+······+47)得

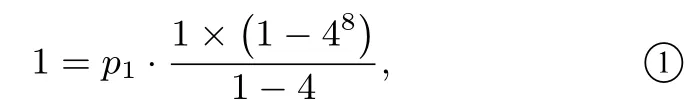
同理p4-p0=p1·(40+41+42+43)，得

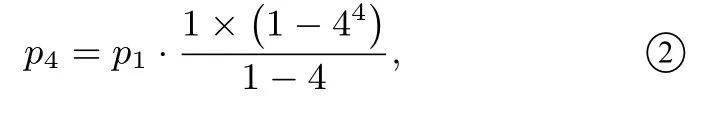
第(2)问(ii)解法3由(i)得解方程组得即表示最终认为甲药更有效的概率.由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8 时，认为甲药更有效的概率为此时得出错误结论的概率非常小，说明这种实验方案合理.

第(2)问(ii)解法4由(i)有pi+1- pi= p1·4i(i = 0,1,2,……,7)累加可得 p8- p0= p1·(40+41+······+47)，得解得所以

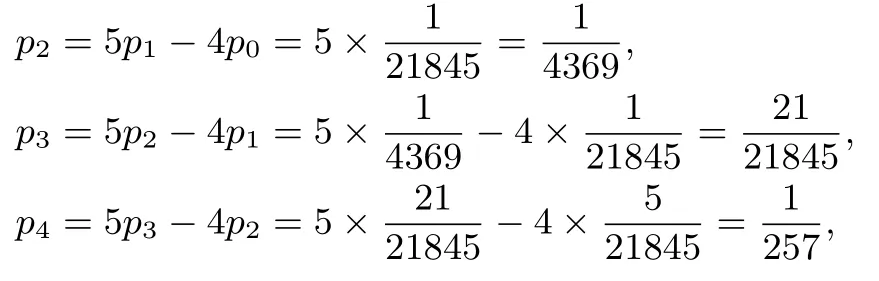
第(2)问(ii)解法5由(i)有

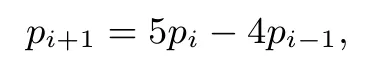
所以

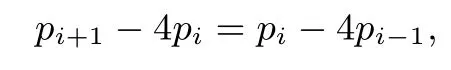
可得

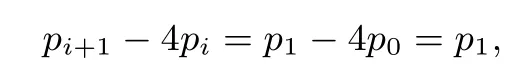
即

又

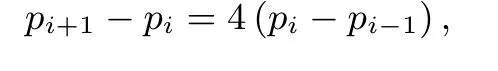
可得

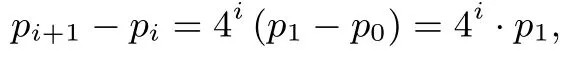
即

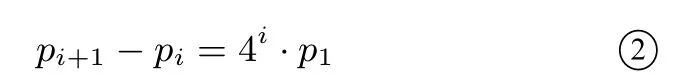
由 ① ②可得3pi=(4i-1)· p1，即由p8= 1，可得所 以p4=表示最终认为甲药更有效的概率.由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8 时，认为甲药更有效的概率为此时得出错误结论的概率非常小，说明这种实验方案合理.

第(2)问(ii)解法6由

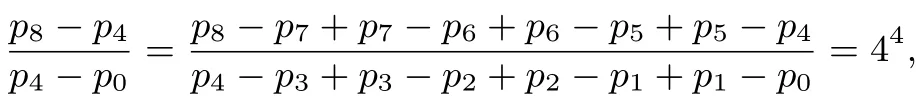
又p8=1，p0=0，得表示最终认为甲药更有效的概率.由计算结果可以看出，在甲药治愈率为0.5，乙药治愈率为0.8 时，认为甲药更有效的概率为此时得出错误结论的概率非常小，说明这种实验方案合理.

3.探究试题中初始条件与递推公式的由来

进一步思考：试题中所给出的初始条件p0= 0，p8= 1和递推公式pi= api−1+bpi+cpi+1是否合理? 能否根据题意推出初始条件和递推公式呢?

事实上，是不需要给出初始条件和递推公式的，这些可以根据题意推出来!

因为依题意，当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时，就停止试验，并认为治愈白鼠只数多的药更有效.甲药、乙药在试验开始时都赋予4 分，pi(i=0,1,···8)表示“甲药的累计得分为i 时，最终认为甲药比乙药更有效”的概率，依照约定，可知每轮得分之和均为0，于是两人得分之和始终不变，保持是8 分.每多治愈一只白鼠则比对方多得2 分，则若甲得0 分，则乙得8 分，故乙治愈的白鼠比甲多4 只，即实验即可停止，故有p0=0，同理p8=1.

若甲得分为i，考虑下一轮，要么变为i - 1，要么不变，要么变为i + 1，其相应的概率恰为a,b,c.从而得到pi= api−1+ bpi+ cpi+1，其中a = P(X = -1)，b=P(X =0)，c=P(X =1).

所以试题完全可以不给初始条件p0=0，p8=1 和递推公式，试题把最难的求递推公式直接给出来，实际是为了降低难度.而且问题(2)(i)的证明等比数列其实也是可以不要的，之所以要证明等比数列也是为了增加梯度，是命题老师给考生提示解题思路的.这样做的目的是为了控制整个试题的难度，让考生相对更容易解答.

当然如果试题不给初始条件和递推公式，直接问最后一问，那样试题的难度就大大的提升了.

4.试题的概率论背景

这道概率题是命题人站在随机过程的马尔科夫链(Markov Chain)角度命制的题目.马尔可夫链，又称离散时间马尔可夫链，因俄国数学家安德烈·马尔可夫得名，是状态空间中经过从一个状态到另一个状态的转换的随机过程.该过程要求具备“无记忆”的性质：下一状态的概率分布只能由当前状态决定，在时间序列中它前面的事件均与之无关.这种特定类型的“无记忆性”称作马尔可夫性质.在马尔可夫链的每一步，系统根据概率分布，可以从一个状态变到另一个状态，也可以保持当前状态.状态的改变叫做转移，与不同的状态改变相关的概率叫做转移概率.下图是一种最简单的马尔科夫链：随机游走(Random Walk)的示意图，这是概率论中著名的“直线上的随机游走问题”.本试题相当于是随机游走的一个变种，增加了一种分数维持不变的可能性.本题相当于有两个边界0 和8，到达边界后即停止，所以更准确的说是“有双侧吸收壁的直线上的随机游走问题”.

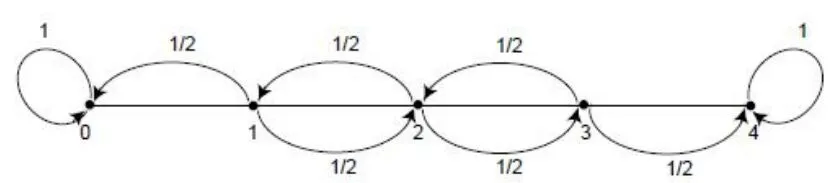
图2

马尔科夫链的本质较为简单，就是一个事件之后的状态只取决于上一步的状态.例如在本试题中，第i+1 次实验之后两种药的分数，只会基于第i 次试验之后的分数+1/不变/-1，所以再之前的分数是多少就不用关心，知道第i 次实验之后的分数就足够对之后继续推测了.

题目中甲药的分数就是这样一个马尔科夫链，而我们关心甲药的分数和最后“试验表明甲药更有效”的概率之间的关系.这就要关系到甲药在不同分数之间转移的概率，就是题目中所给的递推式：pi=api−1+bpi+cpi+1，这个关系式本质上表达了这个马尔科夫链的传递规律，从pi有概率a 传递到pi−1，有概率b 留在pi，有概率c 传递到pi+1.所以从pi出发，最后获胜的概率也是如此传递的.给出这个关系式实质上大大降低了题目的难度，避免了考生因为不熟悉题目的背景而束手无策.试题设计注重对问题背景的理解，将大学随机过程的知识融在高中数列的角度中让考生分析，本质上只需要高中数学的数列知识，而不需要复杂的计算工具.

马尔科夫链是概率论中重要的一类问题，应用非常广泛，有兴趣的读者可以查阅概率论的专业书籍进一步学习.

5.试题的变式

变式1变pi为qi，其中qi(i=0,1,2,····8)表示“乙药的累计得分为i 时，最终认为乙药比甲药更有效”的概率.

变式2变α,β 的值，如α=0.5,β =0.6.

变式3变试验方案设计.

限于篇幅，变式的解答留给读者.

6.一组与本题解答无关的有趣数据

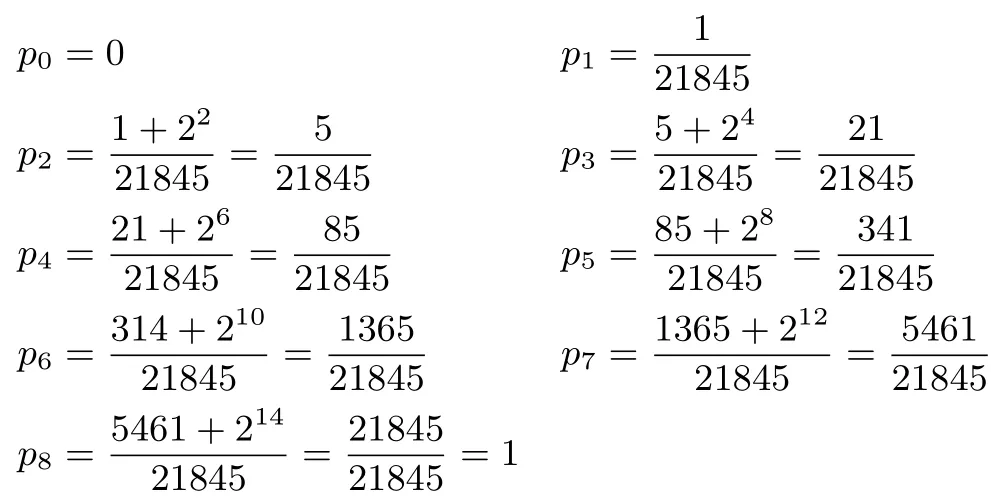
四.教学建议

1.夯实基础，注重对数学概念的教学

概率与统计中的概念众多，在复习备考过程中引导学生回归教材，对教材中的基本概念进行梳理.下面的三条主线可以将概率统计的有关概念串联起来：

一是随机事件的基本研究过程：随机事件→事件概率→基本概型.

二是随机变量的基本研究过程：随机变量→概率分布→分布模型.

三是统计的基本研究过程：收集数据→整理数据→分析数据→统计推断.

2.加强阅读理解能力与数据处理能力的培养

数据处理的一般过程是：用抽样方法收集数据，用统计图表整理数据，用数字特征分析数据，用估计思想作出推断.即“图表→信息→公式→模型”，体现了数据处理的四个层次.

概率与统计是高考试题中相对独立的一个模块，处理问题的方式、方法体现了较高的思维含量.该类问题以应用题为载体，题材内容非常丰富，生活背景知识特别广泛，注重考查考生的应用意识、阅读理解能力、计算能力、分类讨论与化归转化能力.重视概率与统计的理论知识与实际生活相结合，其中题目文字描述多，对考生的阅读理解能力要求高，重视审题教学，教会学生准确理解题意，时刻思考考题已知的是什么，要求的是什么.能从大量的信息中提取对研究问题有效的信息，并做出判断，这是数据处理能力的基本要求，也是解概率统计题的基本要求.

3.突出概率，重视统计

明确概率问题的核心是概率计算，概率计算的核心是清楚事件的互斥、对立、独立等关系.排列组合是进行概率计算的工具，强调概率中的三个基本问题—概率分布列、数学期望、方差，对相互独立事件的概率、超几何分布、二项分布等题型要熟练掌握.

统计问题的核心是样本数据的收集和整理方法，重点是频率分布直方图、茎叶图和样本的数字特征.注意随机数模拟求概率，随机数表法求概率的小题.同时要学会概率与频率分布直方图、正态分布、独立性检验与线性回归方程知识的综合应用、决策问题等.

概率统计是考查数学能力的大舞台，新课程标准中提出的四种能力、六种数学核心素养，在今年的概率与统计试题中除空间想象能力外，几乎全面涉及.

4.关注易错点

在概率与统计复习中，要准确理解概念，特别要明确概率计算的核心是事件之间的关系，统计问题的核心是样本数据的收集和整理，即随机抽样和用样本估计总体.

易错点主要有：

①套用公式计算出错；

②事件之间的关系理解不正确；

③使用排列组合公式时出错；

④频率分布直方图、茎叶图的基本概念理解不清；

⑤二项分布、超几何分布分辨不清；

⑥应用独立性检验方法解决问题时出现K2值计算错误等.

5.想对策

①提高学生的数学阅读能力；

②提高对公式认识的深度；

③加强在教学中对事件的分析，让学生透彻理解事件之间的关系；

④加强排列组合数公式的应用，让学生熟练掌握；

⑤让学生阅读课本，加深对频率分布直方图、茎叶图基本概念的理解；

⑥让学生举例说明超几何分布与二项分布之间的区别与联系；

⑦加强对独立性检验的基本思想的理解与应用.

6.加强数学核心素养的培养及数学思想方法的渗透

高考命题的趋势是以知识为载体，能力立意，思想方法为灵魂，核心素养为统领.概率统计的命题兼顾基础性、综合性、应用性和创新性，以此展现数学的科学价值和人文价值；在全面考查综合数学素养的基础上区分考生的数学能力的差异.因此教师在概率统计复习时，要结合相应的教学内容，落实“四基”，培养“四能”，适当渗透数学思想方法(如数学建模、转化与化归、分类讨论等思想)促进学生数学核心素养(如数据分析与处理、数学运算等)的形成与发展，才能从容应对高考的变化.

7.注重数学模型化思想的渗透

高考中的概率统计问题基本上是应用问题，情景的设置贴近学生的生活实际，对数学建模都有一定的要求.《数学课程标准》中还明确要求教师引导学生建立数学模型，不但要重视结果，更要关注学生自主建立数学模型的过程，让学生在进行探究性学习的过程中科学地、合理地、有效地建立数学模型.帮助学生构建数学模型大致要经过三个大的步骤：①创设问题情境，发现提出问题——建立模型准备阶段； ②探究解决问题——建立数学模型阶段； ③解释应用拓展，体验数学价值——应用数学模型阶段.所以应该加强概率模型的区分与训练，从概率模型入手，分模型训练，以期提高复习的有效性.

8.概率统计教学注意题型的多样性与综合性

数据处理包含面非常广泛，目前主要集中于概率与统计之中.这几年的高考题中，对概率统计的考查要求逐渐提高，背景与题型变化多，且在加大综合性方面进行了探索，如2018年与导数结合、2019年与数列结合充当压轴题，其目的之一是让学生意识到，生活中概率统计的应用非常广泛.特别是人类进入智能化时代后，对数学的分析处理应用更是每个人都必须掌握的一种工作、生活的技能.因此我们要重视概率统计教学，在概率统计教学中注意题型的多样性与综合性，不要因为偏难而选择性放弃，通过有效教学及训练，可以帮助学生克服畏难情绪.

9.作为中学数学教师，需苦练内功，进行高观念下的概率与统计学习

近年来，高考的命题者通过挖掘高等数学中的一些素材来命制高考试题，这种命题现象应该引起老师们的关注.因此中学教师要加强对概率论与数理统计内容的学习，重视其基本原理的研究，提高自身的专业知识素养；当然这并不意味着要将过多的高等数学知识下放到中学里来，加重中学的负担，应该是教师能站在高观点的角度看待问题，找到问题的本质内涵，更好地指导中学的数学教学.