2019年高考全国I卷数列试题分析及备考建议

广东省广州大学附属中学(510000) 韩智明

广东省华南师范大学数学科学学院(510631) 刘 岩

数列是高中数学的重要知识模块之一，是历年高考必考内容，也是广大考生“抢分争分”之地.在高考试卷有关数列的试题通常题量是一大一小，它们也经常作为压轴题出现，大题则稳在17题，与三角考查交替进行，分值约占15 分左右.数列题是考查学生综合素养的重要载体，其蕴含了构造、转化和化归、函数与方程、数形结合等数学思想方法，体现了数学运算、逻辑推理、几何直观等数学学科核心素养.数列备考问题存在题量大、所包含知识面广、题型复杂、难易大小程度区分大且文理不同科考查要求不易把握等情形；近几年的高考都是把数列作为核心内容来考查，从总体上来看，难度虽然有所降低，但是创意不断，而且是常考常新.本文通过对高考全国I卷数列题的分析，从文理科数列考题在知识要求、思想方法、能力及核心素养考查等角度进行探讨，旨在为2020 届高三数学数列复习备考提供一个参考，也期望对高三文理科教师进行复习备考时起到一个较为明晰的教学引领和导向作用.

1.试题分析

1.1 试题呈现

题目1(2019年高考全国I卷文科第14题)记Sn为等比数列{an}的前n 项和.若则S4=____.

题目2(2019年高考全国I卷理科第9题)记Sn为等差数列{an}的前n 项和.已知S4=0，a5=5，则( )

A.an=2n-5 B.an=3n-10

C.Sn=2n2-8n D.

题目3(2019年高考全国I卷理科第14题)记Sn为等比数列{an}的前n 项和.若则S5=____.

题目4(2019年高考全国I卷文科第18题)记Sn为等差数列{an}的前n 项和，已知S9=-a5.

(1)若a3=4，求{an}的通项公式；

(2)若a1＞0，求使得Sn≥an的n 的取值范围.

题目5(2019年高考全国I卷理科第21题)为治疗某种疾病，研制了甲、乙两种新药，希望知道哪种新药更有效，为此进行动物试验.试验方案如下：每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠，随机选一只施以甲药，另一只施以乙药.一轮的治疗结果得出后，再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4 只时，就停止试验，并认为治愈只数多的药更有效.为了方便描述问题，约定：对于每轮试验，若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1 分，乙药得-1 分；若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1 分，甲药得-1分；若都治愈或都未治愈则两种药均得0 分.甲、乙两种药的治愈率分别记为α 和β，一轮试验中甲药的得分记为X.

(1)求X 的分布列；

(2)若甲药、乙药在试验开始时都赋予4 分，pi(i =0,1,··· ,8)表示“甲药的累计得分为i 时，最终认为甲药 比 乙 药 更 有 效”的 概 率，则p0= 0，p8= 1，pi=api−1+bpi+cpi+1(i = 1,2,··· ,7)，其中a = P(X = -1)，b=P(X =0)，c=P(X =1).假设α=0.5，β =0.8.

(i)证明：{pi+1-pi}(i=0,1,2,··· ,7)为等比数列；

(ii)求p4，并根据p4的值解释这种试验方案的合理性.

1.2 试题解析

题目1 解析设等比数列的公比为q，由已知S3=a1+a1q+a1q2=1+q+q2=即q2+q+=0，解得q =所以

另解：本题在求得数列的公比后，可利用已知计算S4=S3+a4=S3+a1q3=避免繁分式计算.

题目2 解析题目2 解析：设等差数列的公差为d，由题意可知解得所以an=2n-5，故选A.

另解：本题还可用排除法：由于a5= 5，若B 正确，则有矛盾，故B 不成立； 若C 正确，则S4= 0，a5= S5-S4= 2×52-8×5-05，矛盾，故C 不成立； 若D 正确，则S4= 0，a5= S5-S4=矛盾，故D 不成立.

题目3 解析设等比数列的公比为q，由已知a24= a6，所以又所以q = 3，故

以上三个题目都是考查数列的定义概念、性质，题目的难度不大，注重了基础知识、基本计算能力的考查.主要考查等差(等比)数列通项公式与前n 项和公式，渗透方程思想与数学计算等学科素养.利用等差(等比)数列通项公式与前n项公式即可列出关于首项与公差(公比)的方程，解出首项与公差，再适当计算即可.

题目4 解法一(1)设等差数列{an} 的公差为d.由S9= -a5得a1+4d = 0，由a3= 4 得a1+2d = 4，解得a1=8，d=-2，故数列的通项公式为an=10-2n.

(2)由(1)得a1= -4d，故an= (n - 5)d，Sn=由a1＞ 0 得d ＜ 0.故Sn≥ an等价于n2- 11n +10 ≤0，解得1 ≤n ≤10.所以n 的取值范围是{n|1 ≤n ≤10,n ∈N}.

题目4 解法二(1)设等差数列{an} 的公差为d.S9= 9a5，由S9= -a5得a5= 0，由a3= 4 得d = -2，由于an=a5+(n-5)d，故数列的通项公式为an=10-2n.

(2)由(1)得a1= -4d，故由a1＞0，故Sn≥an等价于n2-11n+10 ≤0，解得1 ≤n ≤10.所以n 的取值范围是{n|1 ≤n ≤10,n ∈N}.

题目4 解法三(1)同解法一或二；

(2)由(1)得a1=-4d，

①当n = 1，S1= a1成立，由Sn≥an得na1+整理得(n-1)d；

由 ① ②可知1 ≤n ≤10.

题目4 解法四(1)同解法一或二；(2)由(1)得a1=-4d.

①当n=1，S1=a1成立；

②当n ≥ 2 时，由an= Sn- Sn−1代入Sn≥an得Sn≥ Sn- Sn−1，即Sn−1≥ 0，即(n - 1)a1+同除n-1 得即即n ≤10.

由 ① ②可知1 ≤n ≤10.

题目4 解法五(1)同解法一或二；

(2)S9= 9a5或a5= a1+4d = 0，由S9= -a5得由a1＞0 得d ＜0，则由a1＞0 得，d ＜0，则an＜0(n ≥6)，当1 ≤n ≤5 时，Sn= a1+···+an≥an，当n ≥6 时，{Sn}是递减数列，由Sn≥an得Sn−1≥0=S9，则n-1 ≤9，所以1 ≤n ≤10.

题目5 解法参见参考文献[2]，不再赘述.

1.3 试题评析

1.3.1 文理科数列知识考纲考查要求如下表

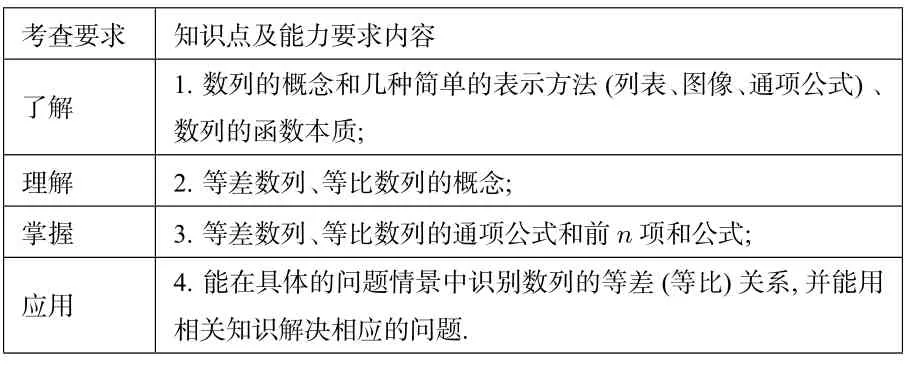
考查要求知识点及能力要求内容____________________________________了解1.数列的概念和几种简单的表示方法(列表、图像、通项公式)、数列的函数本质；________________________________________理解2.等差数列、等比数列的概念；______________________________掌握3.等差数列、等比数列的通项公式和前n 项和公式；___________应用4.能在具体的问题情景中识别数列的等差(等比)关系，并能用相关知识解决相应的问题._________________________________

1.3.2 文理科数列能力考纲考查要求

考纲中明确规定高中数学学习要培养的数学能力是指：空间想象能力、抽象概括能力、推理论证能力、运算求解能力、数据处理能力以及应用意识和创新意识.数列知识模块涉及到的数学能力主要有：①推理论证能力，②运算求解能力，③应用意识和创新意识.

1.3.3 文理科数列数学思想、方法考纲考查要求

考纲中提出高中数学学习要具备的七大基本数学思想方法是指：函数与方程思想、数形结合思想、分类与整合思想、化归和转化思想、特殊与一般思想、有限与无限的思想、或然与必然的思想.数列知识模块涉及到的数学思想方法主要有：①函数与方程思想，②分类与整合思想，③化归和转化思想，④特殊与一般思想，⑤数形结合思想.

1.3.4 考题考查到的知识、能力、思想方法、核心素养如下表

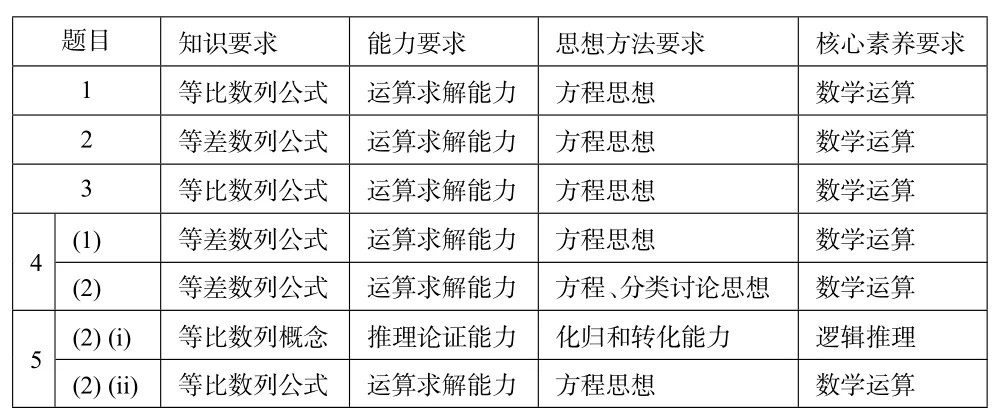
题目知识要求能力要求思想方法要求核心素养要求__1等比数列公式运算求解能力方程思想数学运算______2等差数列公式运算求解能力方程思想数学运算______3等比数列公式运算求解能力方程思想数学运算______4(1)等差数列公式运算求解能力方程思想数学运算______(2)等差数列公式运算求解能力方程、分类讨论思想数学运算______(2)(i)等比数列概念推理论证能力化归和转化能力逻辑推理_____5(2)(ii)等比数列公式运算求解能力方程思想数学运算_____

1.3.5 试题综述

今年文理科试卷在数列知识模块的考查中做到了统筹兼顾，展现了稳中有变，变中有新，新中有活的出题特点，坚持以能力立意，以知识为载体，落实核心素养，体现了选拔功能和区分度，对中学数学教学科学导向，从各个角度全面考查学生的数学素养.

文理科都以小题的形式考查了等差数列的定义、通项公式、前n 项和公式与性质，渗透方程思想、化归和转化思想，突显运算能力和推理论证能力，尤其集中对数列必备重点基础知识的考查.

今年较以往有所不同，理科在大题中虽然没有和文科一样专门把数列作为一个大题出现，出乎大家意料地是在压轴概率统计大题中巧妙地植入数列知识，单独成问，重点对递推数列中的等比数列证明和求和进行考查，在概率大题中与数列知识联系紧密，做到了三角和数列在大题中考查的兼顾；文科在大题中对知识层面的考查也一改以往数列求和的套路，通过对二元方程组的求解及简单不等式的化简和求解，考查了学生对基础知识的简单掌握及应用能力、逻辑推理能力、数学运算能力，试题渗透了转化化归、函数与方程、数形结合等思想方法，试题设计新颖、把数列知识和方程、不等式巧妙结合，对考生的综合数学素养进行了较为全面的考查.

2.考生答题情况分析

2.1 典型错误详情参见参考文献[3]，不再赘述.

2.2 考生答题情况错因分析

2.2.1 知识性错误不熟悉等差数列的公式，张冠李戴，乱用公式或自己造公式，不知道数列通项公式的表示方法出现“{an}=10-2n”的常识性错误；对等差数列的概念模糊，利用特殊有限几项通过不完全归纳法得到一般性结论，缺乏严格的推理论证；对题设条件不清楚，大量考生出现依赖第一问结论来解第二问的错误；对不等式的性质不熟，解不等式变形时不考虑字母符号出现不等号不变号的错误n.

2.2.2 方法性错误本题对数列知识模块的考查一改以往特别专注数列求和的特点，在注重数列基础知识的前提下，渗透融合数列和方程、不等式相关知识，特别是设置当考生错误利用第一问结论解决第二问时，同样可以出现相同的答案，对考生的知识辨析能力要求较高；解法四中对不等式中“n-1”的处理没有考虑n 的取值范围直接消掉；解法五中没有说清楚当n ≥6 时，{Sn}是递减数列，由Sn≥an得Sn−1≥0 = S9，则n-1 ≤9，而是直接得到结论，对等差数列的函数性质理解不到位；数列试题应该成为广大考生得分的重要阵地，结果4.5 分左右的平均分，未免让人感慨万分.

2.2.3 能力性错误高考命题不光是凸显知识立意、能力立意，而且已经走向素养立意了，在试题中体现学科核心素养也是体现一道试题价值的核心指标，文科考生发散思维较强，理性思维普遍偏弱，在平时的学习中多偏好按套路解题，不理解数学公式的来龙去脉和本质含义，在第一问中甚至出现一元一次方程组不会解得情况； 试题包含数学知识面广，通过数列问题列出方程组和不等式，出现几次数学思维的转换，考生在哪一方面不熟就会出现错误；试题蕴含数学思想方法较多，在解题过程中函数方程、化归和转化、分类讨论甚至是数形结合思想都有所体现，足以综合考查考生的综合能力；试题考查的数学核心素养也较为丰富，要求考生必须有较强逻辑推理和数学运算方面的数学素养.

3.备考复习建议

3.1 研究高考考纲，把握高考命题方向立足高考考纲，把脉高考命题方向是每位教师在进行备考前的一项重要工作，从近几年的文理高考数列考查内容和方向来分析，变化不大，保持了较高的稳定性，注重考查数列的基本定义和概念，渗透数学思想方法，体现数学能力，考核学科素养，前几年的考查都是从数列的基本通项和求和公式方面重点考查学生的运算能力居多，从2019年的文科数列大题来看，一改画风，把数列知识和方程、不等式等知识结合，具有一定的综合性，对学生的能力要求更高，从整道试题的均分4.5 的得分就可以知道.理科数列试题在大家千呼万唤中今年作为大题中出现(前几年理科大题一直考查三角)，不过不是像大家猜测那样用数列替换三角而独立成题，而是把数列知识巧妙地融合到概率统计压轴题中，巧妙而又自然地对递推数列证明和求和进行了考查，试题体现了数学知识模块之间的互相渗透，从数学能力和学科素养上对学生进行了一次挑战.

作为一线教师，要对高考方向有一个比较精准的判断和预测，除了研究高考试题，还要研究《课程标准》、《考试大纲》与《考试说明》.这三者是高考命题的指挥棒和重要依据，当然研究高考试题也要不局限某年某地，而是要放眼所有年份或省市的高考卷.

3.2 熟悉数列定义，训练学生辨析理解能力在数列知识模块的教学或备考活动中，首先要让学生理解数列的函数本质，体验数列相关公式的推导过程，清楚其来龙去脉，通过不断的变式和训练题来提升学生的运算能力和逻辑推理能力，在解题过程中重点关注学生在计算中出现的高频错点，通过对知识错点的再纠正来加深学生对等差(等比)数列定义的理解，强化对数列一系列公式的记忆，促使学生明晰概念，增强对数列类型的识别能力.

3.3 掌握数列性质，提升学生综合能力数列的定义和概念是学生学习数列知识必须掌握到位的知识，也是我们在进行高考备考务必具备的教学环节，由数列定义而提取的数列性质则是学习数列的重点内容，只有深刻理解数列的定义才能领悟的数列的系列性质，比如：理解了数列的函数本质，你就知道通过数列通项或求和公式就可以对一个数列进行判断，从文科数列解法五可以看出考生充分利用数列性质解答，过程简洁美观，达到事半功倍的效果.熟练掌握和运用数列性质去处理数学中的数列问题，必须在高考备考中通过题组形式对学生进行针对训练，在题组训练中体验数列性质的灵活运用，加深对数列性质的理解.

3.4 理解数列背景，促成学生转化应用能力纵观数列试题的命制，其考查内容离不开定义和性质，只是考查的形式和角度不一样，文科试题把数列知识和方程、不等式相关知识相结合，理科试题把数列知识巧妙自然地“镶嵌”在压轴概率统计题中，它们都是搭载其它数学知识的平台，互为知识背景，体现数学知识之间的自然融合，实现了数学知识之间的完美互动，综合性较强.这种试题命制特点和风格是否预示着为即将到来的文理同卷作铺垫，数学知识的考查不再单一化，而是重在穿插和渗透融合.试题对考生的考查不仅仅局限于数列知识，它要求考生在多个数学知识模块的解题活动中实现多种知识间的思维转换，在其它知识系统中明晰数列知识的角色参与，在数列的知识系统里熟悉其它数学知识的“客串”功能，从而实现知识间的相互转化，试题蕴含丰富的数学学科核心素养.此类题的备考重点是理解数列的本质内涵，熟悉数列知识的背景，提升是学生解题的转化能力.

3.5 挖掘数列本质，达成学生创新思维能力一道试题的命制体现一种思维过程，其考查某种知识内容的形式有显性和隐性之分.理科试题以pi+1= 5pi- 4pi−1递推数列的形式呈现，从表面上看仿佛此题与数列相关知识无关，其实它是隐性地考查等比数列知识.通过仔细观察递推式结构，合理变形和重组，就可以构造等比数列pi+1- pi= 4(pi-pi−1)(i = 1,2,.....,7)来求解，它是以等比数列知识搭建平台，把学生的思维提升到一个源于等比数列而又高于等比数列的高度，综合性强，是运用构造思想解题的典例.文科试题第二问还可以把看做关于n 的二次函数作出图像通过数形结合得到结果，这些解法都是对数列本质内涵的深刻理解后而得到的创新思维，学生只有掌握了数列知识所蕴含的本质问题，才能在解题过程中领悟和转化，触类旁通，化繁为简.在高考复习备考中，我们要求学生在熟练掌握运用数列定义和性质处理相关数学问题的同时，更要深刻理解和挖掘数列的本质，能够运用转化和等价思想巧妙合理地处理看似复杂实则简单的数学问题.