2019年高考全国I卷三角试题评析及复习建议*

中山市教育教学研究室(528400) 方 勇

三角函数集数、形为一体，是沟通几何与代数的桥梁，蕴含了重要的数学思想方法，体现了数学学科的本质，是高中数学的重要内容之一，是历年高考必考的重点部分.

一、考查要求

高中教材三角模块主要有三部分内容：三角函数(基本初等函数)、三角恒等变换、解三角形.2019年考试大纲对此部分规定如下：

表1

表2

表3

由上述表格可以看出，高考主要考查任意角三角函数的概念和正弦函数、余弦函数、正切函数的图像与性质，突出考查三角函数模型的图像与性质；考查两角和与差的三角函数公式和简单的三角恒等变换.重点考查正弦定理和余弦定理及其应用.对三角函数的考查重点是考生对基本概念、基本公式的理解和应用以及运算求解能力.从下文可以看出，2019年高考全国卷很好的体现了考试大纲的要求.

二、试题评析

2019年全国I卷对三角部分的考查与前几年保持基本一致，分值稳定在15 分左右，其中文科采取“2 选1 填”的形式，理科采取“1 选1 大”的形式，试题总体难度中等及以下，以考查基本知识、基本运算(变换)为主，是学生得分的“重头”.

题目1(全国I卷文科第7题)tan 255°=( )

解根据诱导公式及两角和的正切公式有，tan 255°=tan(180°+75°)= tan 75°= tan(30°+45°)= 2+故选D.

本题考查知识点为三角诱导公式以及两角和的正切公式，要求考生能够利用诱导公式将所求“大角”转化为“小角”，再利用两角和的正切公式转化为特殊角的三角函数值进行运算求解.本题对考生的运算化简能力有一定要求，考查转化与化归的思想方法.

题目2(全国I卷文科第11题)△ABC 的内角A,B,C的对边分别为a,b,c，已知a sin A - b sin B = 4c sin C，cos A=则=( )

A.6 B.5 C.4 D.3

解因a sin A-b sin B =4c sin C，由正弦定理得

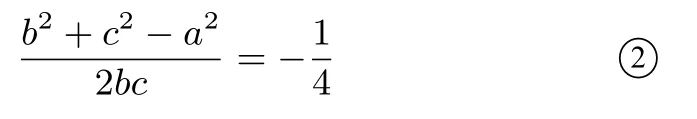
本题考查知识点为正、余弦定理，要求考生能够利用正、余弦定理进行边角转化，根据所求目标对代数式进行合理变形求解.本题对考生的代数运算能力要求显然高于上一题，考查函数与方程的思想方法.

题目3(全国I卷文科第15题)函数f(x)=-3 cos x 的最小值为____.

解f(x)= sin- 3 cos x = -2 cos2x -3 cos x+1，显然fmin(x)=f(0)=-4.

本题考查知识点为三角诱导公式、二倍角公式、三角函数模型，要求考生能够利用诱导公式、二倍角公式将三角函数模型转化为同名三角函数模型，再结合余弦函数的取值范围，通过观察函数表达式来发现最小值.本题对代数变形有一定要求，考查转化与化归的思想方法.

注：本题设计精妙，考生在求得f(x)= -2 cos2x -3 cos x+1 后，可以通过观察函数解析式的特征，快速发现

题目4(全国I卷理科第11题)关于函数f(x)=sin|x|+|sin x|有下述四个结论：

①f(x)是偶函数

③f(x)在[-π,π]有4 个零点

④f(x)的最大值为2

其中所有正确结论的编号是( )

A.① ② ④ B.② ④ C.① ④ D.① ③

解显然，f(x)为R 上的偶函数，f(x)的最大值为2，故 ① ④正确； 当x ∈时，f(x)= 2 sin x，f(x)在上单调递减，故 ②错误； 当x ∈ [-π,π] 时，f(-π)= f(0)= f(π)= 0，f(x)有3 个零点； 故 ③错误；故选C.

本题考查知识点为三角函数(正弦函数)性质，要求考生熟悉正弦函数的图像性质，并能结合备选项，对题目中函数的性质(奇偶性、单调性、零点、值域等)进行分析.本题要求考生掌握研究函数的一般方法，具备一定的推理论证能力，掌握数形结合的思想方法.

注：本题设计方式具有一定新意，类似于多选题，主要是为新高考后命题方式进行一些探索和过渡.

题目5(全国I卷理科第17题)△ABC 的内角A,B,C的对边分别为a,b,c.设(sin B - sin C)2= sin2A -sin B sin C.

(1)求A；

解(1)由已知得sin2B+sin2C-sin2A=sin B sin C，故由正弦定理得b2+ c2- a2= bc，由余弦定理得因为00＜A ＜1800，所以A=60°.

(2)由(1)知B =120°-C，由题设及正弦定理得

即

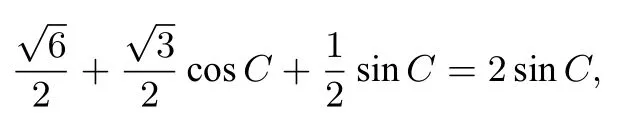
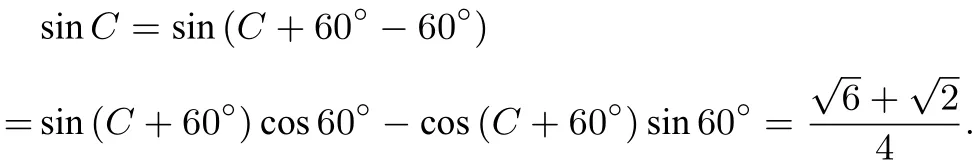
本题依托平面几何中一类相似三角形(有一个内角为60°)为载体，将解三角形相关知识融入其中.第(1)问将余弦定理的代数表达式(关于边的)经过代数变形，再利用正弦定理转换成关于角的关系式，要求学生能正确识别关系式，能联想到并利用正弦定理将角的关系式转化为边的关系式，利用余弦定理求出角.第(2)问来源于人教A 版必须5 第一章《解三角形》1.2 节课后练习第3题(射影定理)，以题中三角形射影定理为背景，在第(1)问条件的基础上增加边的关系(事实上，这确定了一类相似三角形)，要求学生能合理利用第(1)问的结论，根据要求的目标，把边的关系转化为角的关系，通过三角变换求得结果，即求出这类相似三角形的特征(内角).

本题考查的知识模块为人教A 版必须5 第一章《解三角形》章节内容，涉及到的基本知识有正弦定理、余弦定理、三角函数性质(三角函数取值)、三角恒等变换以及三角形基本性质(内角和180°等)等，主要考查的基本能力有运算求解能力、推理论证能力，涉及到的数学核心素养有数学运算素养、逻辑推理素养和直观想象素养.

2019年全国I卷三角考题考点汇总如下：

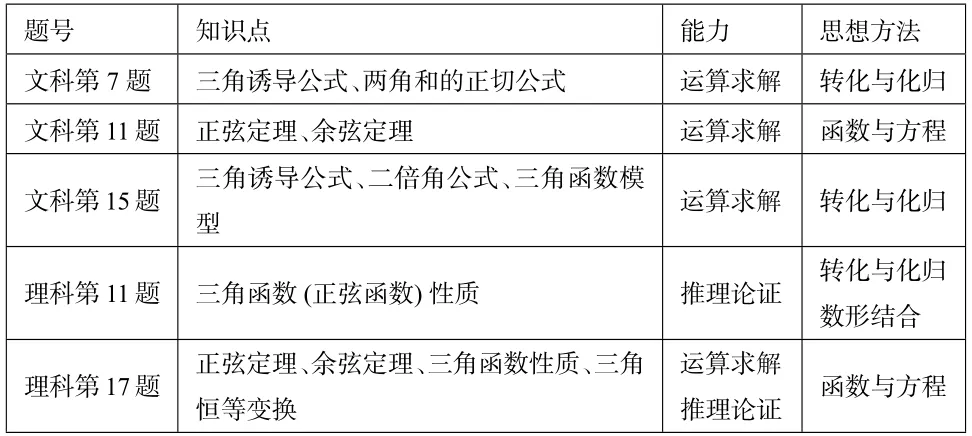
表4

从上面分析可以看出，2019年高考三角部分试题立足于课程标准和考试大纲，以素养为导向，突出能力立意，通过考查学生对基础知识和基本方法的熟练程度，考查学生对重要数学思想方法的理解和掌握，对教学发挥了正确的导向作用.

三、典型答卷及分析

下面以理科17题为例，对考生在答卷中反映出来的问题作简要分析.本题第(1)问较为基础，绝大部分学生(80%以上)能够正确求解，第(2)问对学生运算能力要求较高，还要求学生具备一定的推理论证能力，能对可能出现多解的情况进行讨论，因而具有一定难度和区分度，有超过一半的考生(53%)未能完美解出.比较典型的答卷情况有：

分析书写不规范，这反映考生思维不严密，或学习习惯不好.

2.第(2)问中，停留在√2 sin A+sin B =2 sin C 不知如何继续.

分析说明考生没能掌握解三角形的基本方法.

分析说明考生运算能力欠缺.

分析说明考生三角变换运用能力不够，不能熟练运用辅助角公式.

分析原因同1.

分析算法设计欠佳，导致运算困难.

分析原因同1.

四、备考建议

针对高考三角部分试题的特点，结合上文中考生答卷暴露出来的问题，建议在今后的复习中要注意下面几点：

1.日常教学中要重视教材知识的生成过程，注重数学思想方法的渗透.数学知识的形成与发展经历了一个漫长的抽象、提炼的过程，最终才形成了今天我们看到的科学形态的数学，这个过程凝聚了无数数学家、学者的智慧和汗水，体现了重要的数学思想方法.这些数学思想方法具有迁移性，对学生解决新的数学问题具有启发作用，高考试题也往往在这方面加强考查.比如2019年高考三角试题考查了转化与化归、函数与方程、数形结合等思想方法.教师在日常教学中，要抛弃讲题练题的功利化思想，不能为了追求进度，片面追求知识的应用而忽视知识的生成过程，要通过引导学生自主探究、积极思考，深刻地领悟蕴含在知识形成过程中的思想方法.

2.回归教材，用好教材，发挥教材中阅读材料、例题、练习、习题的辐射示范作用.教材是学生数学知识的主要来源，教材知识是学生能力发展的基本生长点，教材内容是高考命题的重要依据和试题来源，许多高考试题是教材中的阅读材料、例题、练习、习题的引申或变式(如本题第(2)问).教师在指导学生复习中要重视教材，引导学生对教材中经典题目进行抽丝剥茧，对解决教材问题中的重要的思想方法进行举一反三，发挥好教材题目的辐射示范作用，学会“万变不离其宗”，从而提高复习效率.

3.强化落实“双基”.注重基础性，注重通性通法，考查学生必备知识和关键能力是高考数学试题的重要特征(这也体现了国家对基础教育培养人才的基本要求).高考通过加强对基本概念、基本原理、基本思想方法的考查，引导学生重视基础，将所学知识和方法内化为自身的能力.如今年理科17题是解答题第一道题，从难度上讲，这是一道中等偏易难度题目，是广大学生拿分的“大头”.但从上文中学生答卷情况来看，情况并不是那么理想.许多学生对解三角形的基本知识、通性通法(边角互化)、基本能力(运算求解)仍然掌握不不到位，这反映出来我们前期的复习中，“双基”落实仍有较大提升空间.因此，教师在复习教学中始终要把落实“双基”作为教学的基本任务，不要一味贪多求快，要帮助学生克服“眼高手低”的不良习惯，基本知识逐一落实，基本能力逐一过关.

4.提升数学表达能力，做到规范答题.规范答题的本质是数学思维的书面表达，要求学生理解、并能灵活运用数学语言将问题解决的方法正确表述出来，体现了思维的严谨性程度和深度，也反映了学生学习品质的高低.经历过高考阅卷的教师都很清楚，高考答卷中因为学生不规范书写导致的失分情况比比皆是，看起来非常痛心.学生常犯的答题毛病有：多写废话或少写跳步、忽略关键点、用非标准符号代替书写，以图代证(以几何直观代替数学证明)，用特殊代一般等.这些毛病的养成既与平时教师对学生要求不严格有关，也与教师本身习惯有关(有些教师自己板书也非常随意).冰冻三尺，非一日之寒，希望教师们平时就以身作则，严格要求，帮助学生形成严密思考，规范书写的好习惯.