一道高三模考题的解法探究
☉北方民族大学数学与信息科学学院 何陈程
☉湖北省宜昌市第十七中学 何金华
三角函数是高中数学函数部分的一个重要的组成部分,是高中数学必备的基础知识,同时也是历年高考的重点和热点内容.教材中涉及三角函数的内容主要分为两大块:《必修4》中的“三角函数”与“三角恒等变换”这两章,以及《必修5》中的“解三角形”这一章.虽说多数情况下,考查三角函数知识以基础题和中档题为主,学生失分不会太严重,但是我们也不可掉以轻心,避免“阴沟翻船”,这不,这次全市高三期末联考数学试卷中,第14题出现了一道三角形中的三角函数问题,学生的得分情况只能用一个“惨”字来形容,于是在这里写出来,探究这道题的解法,与大家共勉.
题目在△ABC中,已知sinAsinBsin(C-θ)=λsin2C,其中,若为定值,则实数λ=______.
思路分析:题设条件中给出了而且式子sinAsinBsin(C-θ)=λsin2C中含有θ,这是一种暗示,暗示我们要根据tanθ的值求出sinθ,cosθ的值.因为sin(C-θ)展开后会出现θ的正弦、余弦值,题设中有是定值,那么,我们猜想:要么是将sinA·sinBsin(C-θ)=λsin2C展开后转化成正切形式,要么是将转化成正弦、余弦,总之,只要我们找出这两个式子之间的内在联系,此题离解出正确答案就不远了,下面我们就一起来探讨这道题的解法.
解法1:因为,所以cosθ=2sinθ,4sin2θ+sin2θ=1.又因为,所以,


点评:本解法中,将sinAsinB整体代入是关键,遵循了我们解决这类问题的常规思路,即将正切转化为正弦、余弦来处理.
解法2:将已知等式sinAsinBsin(C-θ)=λsin2C变形处理,可得sinAsinB(sinCcosθ-cosCsinθ)=λsinCsin(A+B),将代入,有sinAsinB·
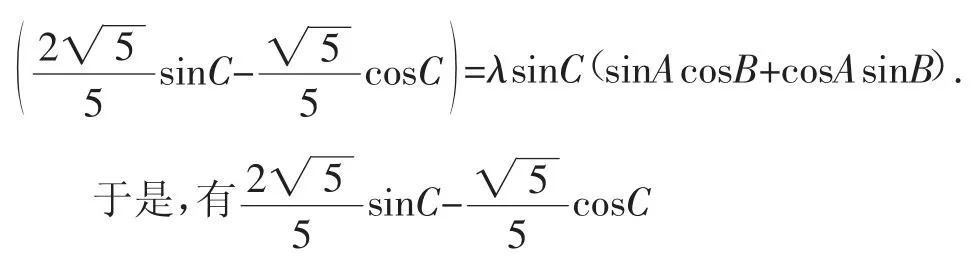

点评:本解法中,将其中一个sinC用sin(A+B)替换,从而将正弦、余弦等式转化构造成已知条件中的的形式是解题的关键.
解法3:将已知等式sinAsinBsin(C-θ)=λsin2C变形处理,可得sinAsinB(sinCcosθ-cosCsinθ)=λsinCsin(A+B),将代入,有sinAsinB·
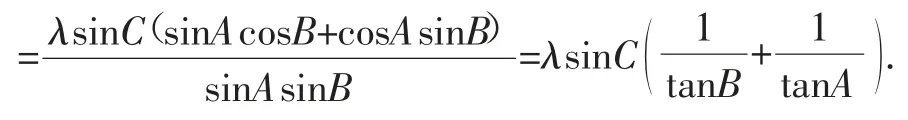
点评:与解法2类似,只是最后一步的处理方式不同而已,解法2是从化简结果看,本解法则从对比已知条件中的正切等式整体形式出发.
解法4:由正弦定理知所以已知等式sinAsinBsin(C-θ)=λsin2C可化为将由已知条件tanθ=求得的代入,有所以2absinC-abcosC=根据余弦定理,可得变形得

点评:在三角形的相关问题中,正弦定理和余弦定理是常用的两个基本定理,在本解法的整个转化过程中,这两个定理的作用体现得淋漓尽致.
变式训练:在△ABC中,角A、B、C所对的边长分别为a,b,c,若且a2+b2+c2=1,则△ABC的面积为______.
思路简析:因为要求△ABC的面积,而面积的公式中是含有正弦值的,所以可先将已知条件中等式处理为然后结合余弦定理,有即=2,再由a2+b2+c2=1即可求得△ABC的面积为
在三角恒等式的处理上,经常会运用三角函数中的一些基本公式、基本定理,平时教学时,我们要让学生熟记这些基本公式、基本定理,这是我们解题的根本所在,要追求一题多解,多指导学生从不同的角度去思考问题,以拓宽学生的数学思维空间.

