基于数学核心素养的微专题研究——以“与圆有关的高考问题探究”为例

☉江苏省清浦中学 吴洪生

☉江苏省清浦中学 金明

圆是高中数学中一个重要的C级考点，常与另一C级考点直线方程一起考查，它是中学数学一个重要的知识交汇点，在高考中备受命题者的青睐.圆与直线问题在江苏高考中地位突出，常考常新，是高考的高频考点，既可作为中上难度的填空题，也可在应用题或解析几何解答题中考查.

一、以圆为背景的填空题

（一）转化为“直线与圆”的位置关系

例1（南京、盐城2018届高三一模第12题）在平面直角坐标系xOy中，若直线上存在一点P，圆x2+（y-1）2=1上存在一点Q，满足，则实数k的最小值为______.

分析：我们先设出直线上的动点坐标P（x0，y0），根据向量关系式可以写出圆上的动点Q的坐标由于点在圆x2+（y-1）2=1上，可得，即x02+（y0-3）2=9.从而可以发现点P（x0，y0）在圆x2+（y-3）2=9上.由于点P既在直线上，又在圆x2+（y-3）2=9上，所以该问题自然转化为直线与圆x2+（y-3）2=9有公共点，求满足这个条件的k的最小值.

点评：该问题所涉及的范围较广，既考查了直线和圆的方程，还涉及了向量表达式的考查，并且还运用了相关点法求轨迹方程；对学生逻辑推理、直观想象等核心素养的掌握程度要求较高；另外，其对转化、化归思想的综合运用能力要求也较高.

（二）转化为“圆与圆”的位置关系

例2（苏北四市2018届高三一模第12题）在平面直角坐标系xOy中，若圆C1：x2+（y-1）2=r2（r＞0）上存在点P，且点P关于直线x-y=0的对称点Q在圆C2：（x-2）2+（y-1）2=1上，则r的取值范围是______.

分析：先设圆C1上点P的坐标为（x0，y0），那么根据点关于直线的对称关系可以写出点Q的坐标为（y0，x0）.由题目条件点Q（y0，x0）在圆C2：（x-2）2+（y-1）2=1上，可得（y0-2）2+（x0-1）2=1，那么可以发现点P还在圆C3：（x-1）2+（y-2）2=1上.所以问题自然转化为半径未知的圆C1与已知方程的圆C3有公共点，进而求未知半径r的取值范围.

点评：从知识内容来看，该问题结合点关于直线对称的知识来考查圆与圆之间的位置关系，需要学生熟练地掌握点坐标的对称知识；从核心素养来看，对学生掌握数学运用和直观想象两种素养的要求较高；从能力方面来看，主要是考查学生对逆向思维的运用能力，要求学生能够通过圆的位置关系反过来去判断圆的半径.

二、以圆为背景的应用题

例3（2019年江苏高考18）如图1，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）.规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA.规划要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径.已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位：百米）.

（1）若道路PB与桥AB垂直，求道路PB的长；

（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；

（3）在规划要求下，若道路PB和QA的长度均为d（单位：百米），求当d最小时，P、Q两点间的距离.

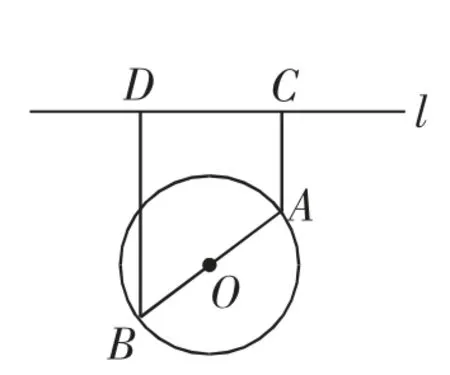
图1

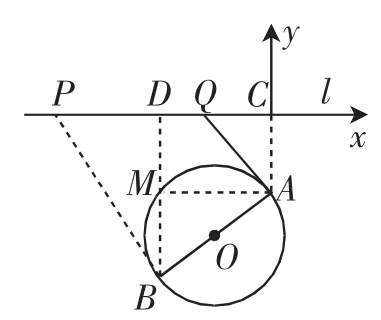
图2

分析：如图2，假设BD和圆O的交点为M，连接AM，AM⊥BD，得到DM=AC=BM=6，AM=8.以点C为坐标原点，l为x轴，建立直角坐标系，则A（0，-6），B（-8，-12），D（-8，0）.

（1）设点P（x1，0），PB⊥AB，则，即，解得x1=-17，所以PB=15.

（2）当QA⊥AB时，QA上所有的点到O的距离不小于圆O的半径，可设Q（x2，0），那么kAQ·kAB=-1，即，解得，所以.因为，在这个范围内不满足PB，QA上的所有点到O的距离不小于圆O的半径，所以P、Q中不能有点选在点D.

点评：这是江苏省2019年高考中的一道以圆为背景的应用题，要求学生能熟练地掌握建立坐标系的方法，求动点间的距离等内容；重在考查学生对数学建模、逻辑推理、数学运用的核心素养的掌握；同时，要求学生具有较强的借助几何图形去解决代数问题的综合运用能力.

三、与圆有关的解答题

例4（2016年江苏高考18）如图3，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2+y2-12x-14y+60=0及其上一点A（2，4）.

（1）设圆N与x轴相切，与圆M外切，且圆心N在直线x=6上，求圆N的标准方程；

（2）设平行于OA的直线l与圆M相交于B、C两点，且BC=OA，求直线l的方程；

（3）设点T（t，0）满足：存在圆M上的两点P和Q，使得，求实数t的取值范围.

分析：将圆M的方程转化为标准方程为（x-6）2+（y-7）2=25，可知M（6，7），r=5.

图3

（1）由已知条件可设N（6，y0），由圆N与x轴相切，并且与圆M外切可知，0＜y0＜7，并且7-y0=5+y0，因此y0=1，圆N的方程为（x-6）2+（y-1）2=1.

（3）先设P（x1，y1），Q（x2，y2），根据已知条件，可知x2=x1+2-t①，且y2=y1+4②.因为点Q是圆M上的点，所以满足（x2-6）2+（y2-7）2=25.将①②代入圆M的方程中，可以得到（x1-t-4）2+（y1-3）2=25.由此可看出点P既在圆（x-t-4）2+（y-3）2=25上，也在圆M上，可知两个圆相交，所以有可解得

点评：从考查的知识内容来看，第（1）问考查了利用圆和直线、圆和圆的位置关系求出圆的方程，第（2）问考查了直线和圆在相交的情况下的问题，第（3）问是动点和向量的综合考查；从核心素养来看，主要考查学生对逻辑推理、数据分析的掌握；从能力方面来看，主要是考查学生运用数形结合思想分析和处理数据的能力.

总之，高考中，与圆有关的知识考查的覆盖面较广，综合性和技巧性都较强，是非常重要的一部分内容，教师在教学过程中，要从数学核心素养的各个方面出发，合理地设计教学方案，帮助学生提高圆的知识的应用能力.