优化高中数学习题课教学“三策略”

☉江苏省启东市第一中学 宋凯东

在当前的高中数学教学中，习题课已经占据着极为重要的地位，是教学过程中具有典型实践性的重要环节，更是对理论内容的深入解读及提升.基于习题课能够促使学生增强运算技能、强化逻辑推理能力，使其可以灵活运用所学知识，并将其运用于分析问题与解决问题的过程中，完成对所学的理论知识的消化与巩固，同时借助习题课还可以检查学生对内容的实际掌握情况.所以，应当全面提高习题课的教学质量，这在高中数学教学中具有极为重要的现实意义.

一、优化师生对话，促进辨析质疑

习题课的教学模式并非是简单的做题和讲题，作为教师，应当关注师生之间的对话，透过对话检测学情，渗透数学思想和方法，以此促进学生对数学相关知识的辨析质疑.

例如，在教学“命题及其关系”练习课时，让学生对以下三个命题的真假性进行判断：

命题1：如果x=2，那么x2=4；

命题2：如果x＞3，y＜4，那么x＞y；

命题3：如果sinα≠sinβ，那么α≠β.

生1：我认为命题1是真命题，命题2为假命题，但是面对命题3，我不能作出准确判断.

生2：应该可以借助举例的方式进行判断.

生3：如果能举出反例，则可以证明其为假命题，但是如果其为真命题，又该怎么办？

师：看起来，针对命题3大家暂时不能作出明确的判断，那么，有没有其他的思考方式或者转换视角进行思考？例如逆否命题.大家是否还记得这四种命题的形式及它们之间的关系？（给予学生相应的思考时间之后投影图1）

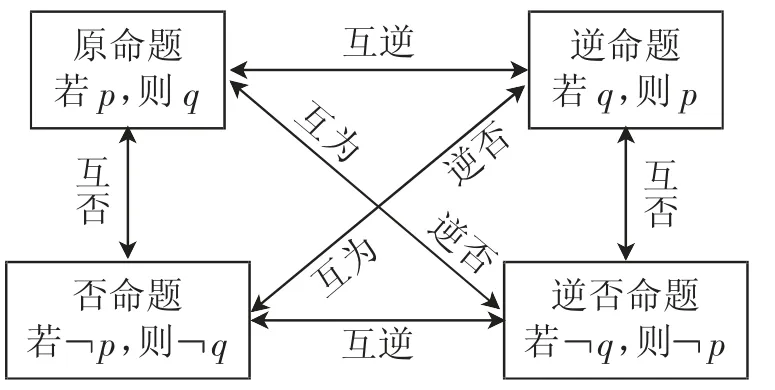
图1

生4：命题3的逆否命题为：若α=β，则sinα=sinβ.很显然，这一命题为真命题，由此也可以帮助我们推断命题3为真命题.

师：刚才我们回顾了四种命题形式及它们之间的关系，我们在实际解题的过程中，可以利用互为逆否命题的判断方法，成功解决对命题3的判断.那么对于这一方法而言，还可以适用于哪些情况？

生5：命题的真假一时间难以直接判断，或者是借助“不等式”的形式而呈现的命题.

师：那么接下来我们看一下命题4：若tanα≠tanβ，则α≠β.

生6：这应该是个真命题.

师：那么它的逆否命题为何？

生6：若α=β，则tanα=tanβ.

生7：如果α=β=90°时，不管是tanα或者tanβ都是不存在的，由此可以看出命题4为假命题.

师：回答得非常完整，我们在研究函数问题的过程中，必须要以定义域为起点开始研究.

在上述教学片段中，教师对教学设计作出了精心的安排，所展示的一组习题由易到难，既明确了教学目的，同时借助师生对话提高了教学实效，学生在教师的及时引导和点拨下，自主展开辨析质疑，由此形成认知上的共鸣.通过这一过程，既完成了对所学知识的巩固，同时也让学生对数学方法的掌握更加到位.

二、优选数学习题，培养思维能力

在高中数学习题课中，作为教师必须要结合教学目标及学情，这样才能够有针对性地选择恰当的习题.同时，在选择习题的过程中，也要注重对课本内容的挖掘.课后习题大都经过专家的精心筛选，可谓精品，但是针对习题的选择也不可完全拘泥于教材，应当要贴合学情才能够更充分地发挥习题应有的功能.

1.借助典型习题，促进举一反三

在数学这门学科中有一些典型的习题，它们大都具有较强的解题思路和解题模式，实际训练的过程中，可以结合不断的反思与总结，促使学生对此类习题形成模型化的解题思路，以达到举一反三的效果.

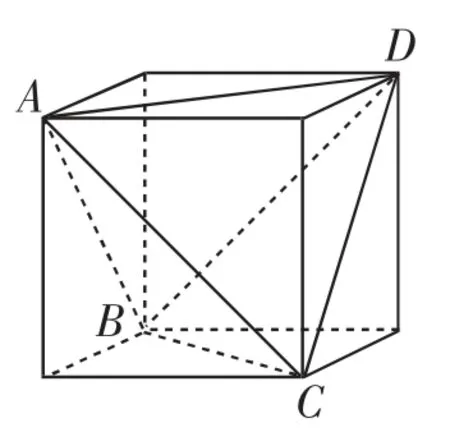
图2

例1一个正四面体ABCD的所有棱长都为，同时四个顶点都在同一个球面上，求此球的表面积.

对于这一道题，以正四面体的各条棱为侧面对角线，以此构造出一个棱长为1的正方体，假设球体的半径为R，根据正方体对角线的长度为球的直径可以得出，由此可以推断出，进而得出球的表面积为S=4πR2=3π.

这样，借助构造数据模型的方式，既能够使问题的呈现更直观、更形象，同时也巧妙地简化了解题方法，使烦琐的问题变得易于解决.数学模型的固化可以促使学生强化知识间的纵横联系，也能够引发学生的探究兴趣，最为关键的是培养了学生的立体思维及创造性思维.

2.借助易错习题，引导数学辨析

作为教师，应当关注习题中的易错点，并充分发掘其中潜在的教学价值，改变传统的告知教学模式，转向引发学生自主探究的模式.通过教师的积极引导，促使学生自主纠错、自主反思，直至走向成功，并就此生成正误知识的辨析点，这才是帮助学生纠错的最有效模式，关键是在这一过程中还有助于提升学生分析问题和解决问题的能力.

例2已知平面向量a=（x，3）与b=（2，-1）的夹角为θ，如果θ为钝角，求实数x的取值范围.

错误的解题思路集中体现在：因为θ为钝角，由此得出cosθ＜0，进而得到2x-3＜0，推出答案.

因为向量夹角的取值范围是［0，π］，可就此引导学生展开分析：当夹角θ满足条件cosθ＜0时，它一定是钝角吗？正解：因为θ为钝角，所以cosθ＜0，解得.同时，当a和b共线时，还能够得出6+x=0，此时x=-6.这也就意味着a，b的方向相反，所得到的夹角为π，进而推导出实数x的取值范围应该是（

针对习题的教学，教师不但要制定精心的预设，还应当以此作为引领，使学生可以自主发现错误的根源，亲历由错误到完全纠错的辨析过程，真正有助于强化对其知识的透彻理解，这样才能够有效避免类似的错误再次发生.

三、借助有效策略，内化数学知识

在高中数学习题课的教学中，教师要善于通过有效的教学策略，引导学生对数学知识进行内化，这样就能够收到事半功倍的教学效果.

1.引导查漏补缺，形成知识网络

数学知识的学习需要经历一个循序渐进的过程，每一步都要稳扎稳打，这样才能够为下一步的学习奠定扎实的根基，任何一步出现差错，都会影响到接下来的深入学习.为了帮助学生巩固知识，作为教师应当善于发现问题，并且做到及时的查漏补缺，这也对教师提出了更高层面的要求，应当针对学生的练习提炼出具有代表性的错误，这些错误所暴露的必然是学习过程中的薄弱环节或者是教学过程中存在的疏漏.针对这部分习题的选择，并不能仅仅依靠单纯地改变数字，而应当选取考查知识点的练习，这样才能够真正有助于查漏补缺：学生出现错误→订正→再出错→再订正，通过上述过程，及时发现导致错误出现的本质，紧抓源头，才能够使学生汲取教训，才能有助于学生完善认知结构，避免错误的再次发生.

2.借助变式迁移，活化数学知识

在学习新知的过程中，大都以相关知识点作为学习目标，所以技能的掌握一般都会局限于对知识的理解和掌握这一层面，然而接下来所学习的内容及与之相关的知识点还未曾涉及，所以难以实现纵向联系.伴随着学习的逐渐深入，习题中都会呈现出知识的纵向及横向拓展，因此针对习题的选择必须要注重其延伸性，保障深度和广度的拓展，这样才能真正有助于引发学生的深入思考，使其自主地将知识点连成串，厘清知识点之间的关系，充分发挥习题的功能；除此之外，还要关注横向的迁移，使学生可以立足于多个视角、选择多元的方法展开观察和联想，或者结合转化的思想以促进数学思维及灵活度的提高.

总之，在高中数学习题课上，教师应关注习题教学，要紧扣教材以及学情，恰当地选择习题，这样才能真正有助于激活学生参与解题的兴趣，提高其思维的积极性和主动性.