横看成岭侧成峰，多种思维离心率——2019年全国卷Ⅰ理第16题

☉浙江省宁海县知恩中学 何起红

求解离心率是圆锥曲线中最常见的一种题型，一直是高考的热点问题之一，也是历年数学高考、竞赛中比较常见的一类问题.此类问题往往小巧玲珑，常考常新，变化较大.解决圆锥曲线的离心率的关键是寻找椭圆或双曲线中参数a、c所满足的关系式，根据题设条件可灵活运用圆锥曲线的定义与几何性质、解三角形知识、直线的方程、直线的斜率、平面几何的性质等进行综合分析与处理，从而得以解决离心率的求值及取值范围等与离心率有关的问题.

一、真题在线

例（2019·全国卷Ⅰ理·16）已知双曲线1（a＞0，b＞0）的左、右焦点分别为F1、F2，过F1的直线与双曲线C的两条渐近线分别交于A，B两点.若，则C的离心率为______.

二、多解思维

思维角度1.解析几何角度

利用解析几何知识，通过点的坐标、直线的方程、直线的交点及直线的位置关系等建立关系式来破解.

方法1：（交点坐标法）由题可知双曲线C的渐近线方程为

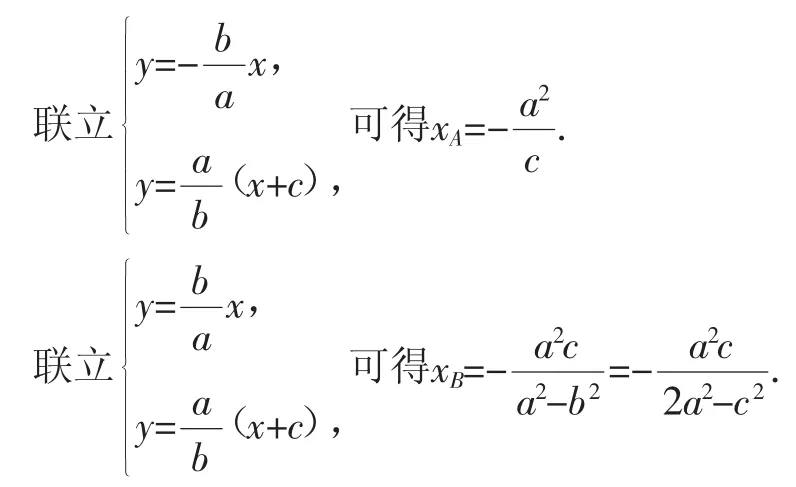
结合A是F1B的中点，可得，整理可得c4-5a2c2+4a4=0，即e4-5e2+4=0，解得e=2（其中e=±1，e=-2舍去）.

故填答案：2.

方法2：（坐标法1）由题可知双曲线C的渐近线方程为

结合直角三角形的性质可得|OB|=|OF1|=c.

故填答案：2.

方法3：（坐标法2）由题可知双曲线C的渐近线方程为

结合直角三角形的性质可得|OB|=|OF1|=c.

而F1（-c，0），由F1B⊥OA，可得，则有b2=a（a+c）=c2-a2，整理可得c2-ac-2a2=0，即e2-e-2=0，解得e=2（其中e=-1舍去）.

故填答案：2.

思维角度2.平面几何角度

利用平面几何知识，通过直角三角形的性质、等边三角形的性质、等面积法思维等建立关系式来破解.

方法4：（等边三角形法）由题可知双曲线C的渐近线方程为

所以∠F1OA=∠F1F2B.

结合渐近线的对称性∠F1OA=∠BOF2，则有∠F1F2B=∠BOF2.

结合直角三角形的性质可知|OB|=|OF2|.

利用∠F1F2B=∠BOF2与|OB|=|OF2|，可知△BOF2为等边三角形，则∠BOF2=60°.

故填答案：2.

方法5：（等面积法）由题可知双曲线C的渐近线方程为

而|OF1|=c，可得|OA|=a，因此有|AB|=|F1A|=b，|F2B|=2|OA|=2a，|F1B|=2b.

结合直角三角形的性质可得|OB|=|OF1|=c.

设点B到x轴的距离为h，利用等面积法有|F1B|·|F2B|=|F1F2|·h，可得

结合xB2+yB2=|OB|2，则有，整理可得4a2=c2，即

故填答案：2.

思维角度3.三角函数角度

利用三角函数知识，通过三角函数的定义、三角恒等变换公式及两直线的夹角公式等建立关系式来破解.

方法6：（夹角公式法）由题可知双曲线C的渐近线方程为

而|OF1|=c，可得|OA|=a，所以|AB|=|F1A|=b.

结合直角三角形的性质可得|OB|=|OF1|=c.

故填答案：2.

三、解后反思

在平时做题时，不能满足于把题目解决出来就可以了，还应该尽量思考不同的解法，从不同角度加以切入，并比较不同方法之间的异同点，从而归纳出常见解法与优异解法.通过不断追求一题多解，一题多思，对思维品质的追求与提升有很好的帮助，这比单纯地追求数量的“刷题”显得更为重要.