一图多问 促进思维 提升素养——以高三《椭圆》一轮复习第1课时为例

☉江苏省梅村高级中学 汪 俊

数学核心素养是数学课程目标的集中体现，是具有数学特征的思维品质、关键能力，以及情感、态度和价值观的综合体现.数学核心素养是在数学学习和应用的过程中逐步发展起来的，是通过数学的反思、积累和升华孕育出来的，如何在高三数学教学过程中落实德育，又充分发挥复习课的功能，教会学生以不变应万变，在减负中提升学生的数学核心素养？笔者以一节椭圆复习课为例，通过一图多问，改变传统的复习方式，对同一图形的提问进行多角度思考与分析，提升学生思维的广度和深度，从而达到培养学生数学核心素养的目的.

一、教学片段与评注

片段1

问题1：观察如图1所示的椭圆，你能得到哪些信息？

学生之间相互讨论补充，得到椭圆的焦点在x轴上，标准方程为，焦距为2.

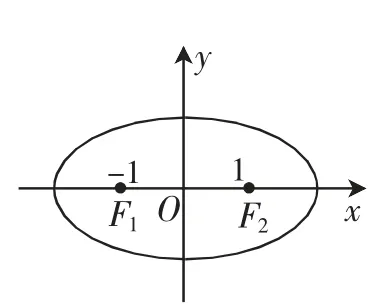
图1

问题2：你能求出该椭圆的方程吗？为什么？若不能，你能添加一个条件使得椭圆的方程能够求出来吗？

生1：不能直接求，可以添加长轴端点的坐标得到a，再求b，或添加短轴端点的坐标得到b，再求a，从而得到椭圆方程.

生2：也可以添加椭圆的离心率e，然后求出a，从而得到椭圆方程.

师：还能添加其他条件吗？

生3：添加椭圆上除端点外的任意一点的坐标也可以，如添加椭圆过点，求椭圆的方程.

师：很好！由生3的条件我们一起来求一下椭圆的方程？

师生共同分析，通过待定系数法，先设出椭圆的标准方程，但要注意先定位，再定量.有时要分类讨论焦点在x轴上还是在y轴上；也可以利用椭圆的定义，直接利用椭圆上任意一点到两焦点的距离之和为2a，然后求出a，再求出椭圆的方程.

评注：通过两个开放性的问题，以题目带动知识，让学生在问题解决中复习椭圆的相关知识，让学生在问题中复习待定系数法、定义法来求椭圆方程的注意点及步骤，渗透分类讨论、数形结合的思想，注重方法的多样性和思维的发散性.

片段2

问 题3：如图2，若P（x0，y0）是椭圆上的任意一点，连接PF1，PF2，你能提出哪些问题呢？

先让学生独立思考，然后交流分享，最后归纳学生提出的问题，主要有：求PF1+PF2的值、△PF1F2的周长和面积、∠PF1F2的度数达到最大值时P的位置、焦半径PF1，PF2的求法等.

师：大家提出的问题都很好，下面我们重点来讨论如何求出PF1，PF2的长度？

生4：利用两点之间的距离公式可知：

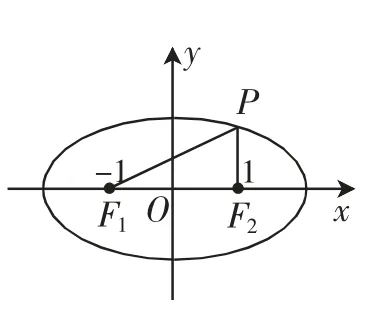
图2

所以PF1=a+ex0，同理PF2=a-ex0.

师：很好！有没有同学有其他的解法呢？

生5：利用椭圆上任意一点到焦点的距离与到相应准线的距离之比是离心率e可得，化简整理得PF1=a+ex0，同理PF2=a-ex0.

师：这位同学利用了椭圆的第二定义，运算较为简单，非常好！接着老师引导大家利用PF1，PF2的长度表达式去研究P点在何处时，∠PF1F2最大.

评注：提出问题比解决问题更重要，在此环节中，教师主动引导学生提出问题并解决问题，在图形中研究问题，让学生的思维层次不断提升，注重问题本质的揭示和方法的提炼，渗透数学思想，有利于培养学生思维的深刻性.同时不满足于问题的单一解决方法，引导学生多角度、多方法来解决问题，不仅强化了知识之间的联系，同时培养了学生思维的发散性和广阔性.

片段3

图3

问题4：如图3所示，若点P（x0，y0）是椭圆上在第一象限内的任意一点，A为长轴端点，B为短轴端点，连接AB，你又能提出哪些问题？并尝试解决.筛选学生提出的问题并归纳如下：

①若△PAB是等腰三角形，求P点坐标.

②是否存在点P，使得△PAB是直角三角形？若存在，求出P点坐标；若不存在，请说明理由.

③过点P作y轴的平行线交AB于点E，则PE长的最大值为多少？

④△PAB的面积的最大值为多少？

教师首先肯定这四个问题都值得研究，然后引导学生重点探究后面两个问题.

师：这是建立了PE关于θ的函数关系式，建立函数模型，很好！

师：上面的解法非常好，我们通过三角代换顺利地解决了与椭圆有关的最值问题，这也是我们经常用到的方法.我们能否用这个方法来解决下面这个问题呢？

问题5：如图4，求出P点到直线AB的距离PQ的最大值.

图4

师：很好！你把求PQ的最大值转化为求△PAB面积的最大值，能否不通过求△PAB的面积而直接表示PQ的长？

教师引导学生可以从三角代换出发设出P点的坐标后运用点到直线的距离公式，或者发现PQ=PEsin∠ABO，从而把求PQ的最大值转化为求PE的最大值.最后通过几何画板来演示，让学生直观感受到：过点P作AB的平行线，当平行线与椭圆相切时，PQ最大，这也是得到PQ最大值的一种方法.

评注：由定点变动点，问题层层推进，水到渠成，学生通过自己提出问题，培养问题意识，通过一题多解，多题归一，在问题解决中提高学生解决与椭圆有关的线段最值、三角形面积的最值问题的能力，增强学生的问题意识和应用意识，注重问题本质的揭示，渗透换元和转化的思想.

二、教学反思与总结

1.改变方式，激发兴趣

数学复习不能简单的重复，否则会让学生觉得枯燥无味，从而失去了学习的兴趣，应该把能力的培养转化为技能的训练.所以我们在高三复习过程中要不断地推陈出新，改变复习方式，在复习形式上创新，让学生在梳理知识的同时，感悟数学解题策略，提炼数学基本方法，从而达到增长智慧、提高素养的目的.本节课突破原来的“知识复习—例题分析—巩固运用—拓展升华”的教学模式，巧妙运用一图贯穿一课的方式，在图中不断添加条件，提出问题，层层深入，逐步衍生出所要复习的知识和方法，从而达到复习的目的.

2.思想渗透，提升素养

在高三复习课中，学生已经较为全面地掌握了基础知识，教师更有条件在教学中有意识地向学生渗透数学思想，揭示数学本质，让学生在应用中体会感悟，在反思中明晰升华，让课堂因思想而厚重.本节课通过问题链接知识，用思想引领方法，抓住图形变化的核心，让学生经历问题的逐渐递进、深度探究，从而提升学生的核心素养.

所以在高三复习中也应该放慢脚步，把更多的时间留给学生思考，把动手的机会、表达的机会、反思的机会让给学生，从而达到促进思维、提升素养的目的.