函数的图像和性质复习要点分析

■河南省太康县第一高级中学

【考点定位】

函数的图像与性质历来是高考的重点,也是热点,对于函数图像的考查主要体现在两个方面:一是识图;二是用图,即通过函数的图像,利用数形结合的思想方法解决问题。对于函数的性质,主要考查函数的单调性、奇偶性、周期性;函数的奇偶性、周期性往往与分段函数、函数与方程结合,考查函数的求值与计算;以指数函数、对数函数、二次函数的图像与性质为主,结合基本初等函数的性质综合考查分析与解决问题的能力。在近几年的高考试卷中,选择题、填空题、解答题三种题型,每年都有函数试题,而且常考常新。以基本函数为背景的应用题和综合题是高考命题的新趋势。在大题中以导数为工具研究讨论函数的性质及不等式求解等综合问题。纵观近几年的高考题,函数问题的考查,往往是小题注重基础知识基本方法,突出重点知识重点考查,大题则注重在知识的交汇点处命题,与不等式、导数、解析几何等相结合,综合考查函数与方程思想、转化与化归思想、分类讨论思想及数形结合思想的理解运用,考查分析与解决问题的能力、应用意识及创新能力。

【典型例题解析】

例1 (2018届北京市昌平区临川育人学校1 2月月考)已知函数f(x)=且a≠1)的最大值为1,则a的取值范围是( )。

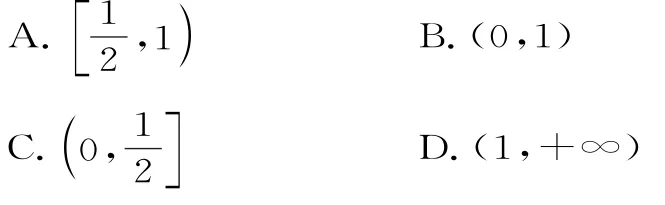
解析：因为当x≤2时,f(x)=x-1,所以f(x)max=f(2)=1。因为函数f(x)=且a1)的最大值为≠1,所以当x＞2时,2+logax≤1,所以解得故选 。A

例2 (2018届北京师范大学附属中学上学期期中)已知m∈R,函数f(x)=1。若函数y=f(g(x))-m恰有6个不同的零点,则m的取值范围是( )。

解析：因为函数f(x)=1,所以当g(x)=(x-1)2+2m-2≤1,即(x-1)2≤3-2m时,则y=f(g(x))=|2g(x)+1|=|2(x-1)2+4m-3|;当g(x)=(x-1)2+2m-2＞1,即(x-1)2＞3-2m时,则y=f(g(x))=log2[(x-1)2+2m-1]。①当3-2m≤0,即时,y=m只与y=f(g(x))=log2[(x-1)2+2m-1]的图像有2个交点,不满足题意,应该舍去;②当时,y=m与y=f(g(x))=log2[(x-1)2+2m-3]的图像有2个交点,需要直线y=m与函数y=f(g(x))=|2(x-1)2+4m-3|的图像有4个交点时才满足题意,所以0＜m＜3-4m,又,解得综上可得,m的取值范围是0＜故选D。

例3 (2019年全国Ⅰ卷理科5)函数f上的图像大致为图1中的( )。

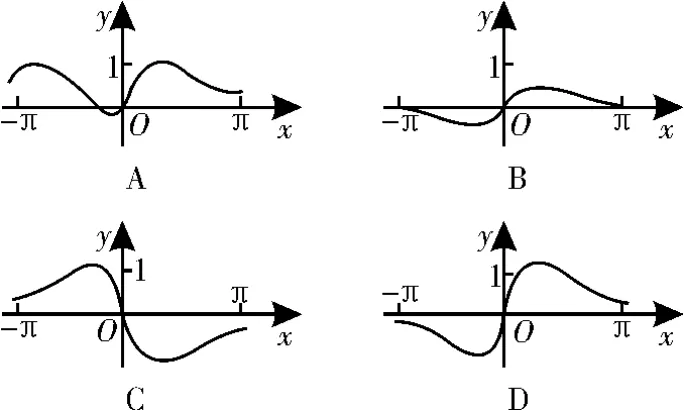
图1

考查意图：考查函数的图像与性质,图像题往往需要与函数的奇偶性、周期性、单调性相结合,再配合特殊值能达到事半功倍的效果。

解析：首先利用函数的奇偶性可以判断函数为奇函数,从而排除选项A,再由特殊点代入得f(π)＞0,可排除选项B,C。故选D。

【复习要点】

1.函数三个性质的应用。

(1)奇偶性:具有奇偶性的函数在关于原点对称的区间上其图像、函数值、解析式和单调性联系密切,研究问题时可转化到只研究部分(一半)区间上。尤其注意偶函数f(x)的性质:f(|x|)=f(x)。

(2)单调性:可以比较大小,求函数最值,解不等式,证明方程根的唯一性。

(3)周期性:利用周期性可以转化函数的解析式、图像和性质,把不在已知区间上的问题,转化到已知区间上求解。

2.函数方程问题求解策略。

(1)判断函数在某个区间上是否存在零点,要根据具体题目灵活处理。当能直接求出零点时,就直接求出进行判断;当不能直接求出时,可根据零点存在性定理判断;当用零点存在性定理也无法判断时可画出图像判断。

(2)已知函数的零点个数求解参数范围,可以利用数形结合思想转化为函数图像交点个数;也可以利用函数方程思想,构造关于参数的方程或不等式进行求解。

(3)对于给定的函数不能直接求解或画出图形,常会通过分解转化为两个函数图像,然后数形结合,看其交点的个数有几个,其中交点的横坐标有几个不同的值,就有几个不同的零点。

跟踪练习：

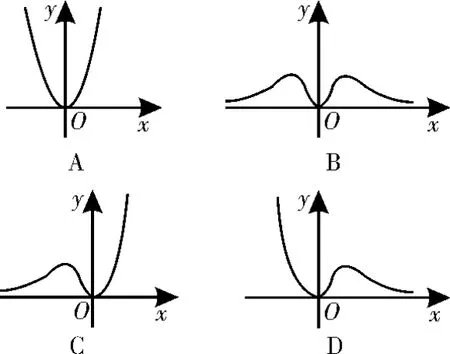
图2

解析：根据题意,函数则,易得f(x)为非奇非偶函数,排除A、B,当x→+∞时,,排除C。故选D。

2.若f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,且f(2)=0,则使得f(log2x)＜0的x的取值范围是( )。

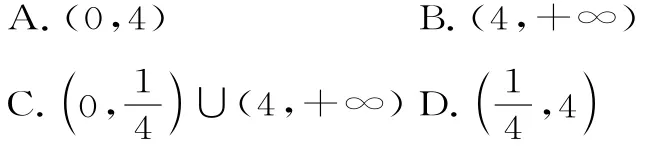
解析：f(x)是定义在R上的偶函数,在(-∞,0]上是减函数,所以在[0,+∞)上是增函数,所以f(log2x)=f(|log2x|),则不等式等价于f(|log2x|)＜f(2),所以,所以,所以x＜4。故选D。

3.若函数f(x)=log2(x+1)的图像与函数y=g(x)的图像关于原点对称,则( )。

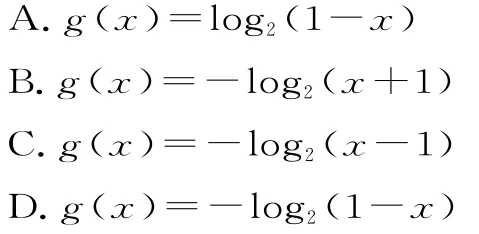
解析：设Q(x,y)是函数g(x)的图像上任意一点,其在函数f(x)图像上关于原点对称的点是P(-x,-y)。因为点P在函数f(x)=log2(x+1)的图像上,所以-y=log2(-x+1),即y=g(x)=-log2(1-x)。故选D。