求解“任意”、“存在”问题的策略
曹吉龙
“任意”、“存在”问题是近几年模拟题及高考题的热点、重点。好多考生对于如何处理这类问题感到无从下手。现举例介绍这类问题的常见的求解策略及方法。
一、“任意”问题的解法
含有“任意的x∈A,使f(x)≥g(x)成立或f(x)≤g(x)成立”这类问题可转化为最值问题或分离参数后转化为最值问题来求解。
【解】(1)略
(2)由g(x)≥-x2+(a+2)x,得 a(x-lnx)≤x2-2x.
∵x∈ [1,]e,lnx≤1≤x,且等号不能同时取得,∴lnx<x,即x-lnx>0
当x∈ [1,]e时,x-1≥0,lnx≤1,x+2-2lnx>0,从而t′(x)≥0
∴t(x)在区间 [1,]e上单调递增,∴t(x)min=t(1)=-1,∴a≤-1
解题策略:任意的x∈A,使f(x)≥g(x)成立⇔x∈A,使[f(x)-g(x)]min≥0;任意的x∈A,使f(x)≤g(x)成立⇔x∈A,使[f(x)-g(x)]max≤0恒成立。
二、“存在”问题的解法
例2.定义在R上的函数f(x)=ax3+bx2+cx+3同时满足以下条件:
①f(x)在(0,1)上是减函数,在(1,+∞)上是增函数;②f′(x)是偶函数;③f(x)的图象在x=0处的切线与直线y=x+2垂直.
(1)求函数y=f(x)的解析式;
(2)设g(x)=4lnx-m,若存在x∈[1,e],使g(x)<f′(x),求实数m的取值范围.
解(1)f′(x)=3ax2+2bx+c.
∵f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
由f′(x)是偶函数得b=0,①
又f(x)的图象在x=0处的切线与直线y=x+2垂直,
∴f′(0)=c=-1,②
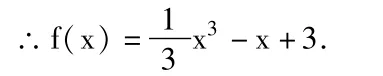
(2)由已知得,若存在x∈[1,e],使4lnx-m<x2-1,
即存在x∈[1,e],使m>(4lnx-x2+1)min.
设M(x)=4lnx-x2+1,x∈[1,e],
我没想到自己的作品会获得如此巨大的曝光,这是让我继续下去的一大动力。以很好的价格出售限量版照片也让我能够自给自足,并且保持创作自由。
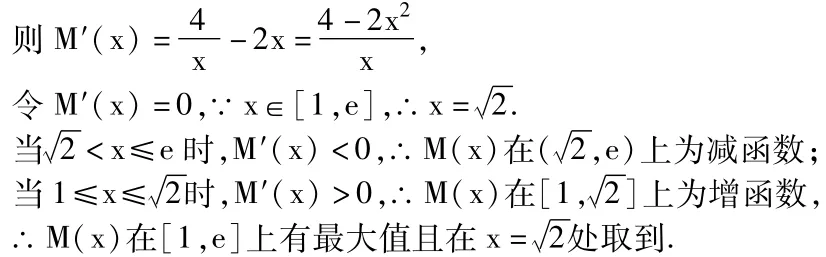
又M(1)=0,M(e)=5-e2<0,
∴M(x)的最小值为5-e2.∴m>5-e2.
评注:存在x∈[1,e],使4lnx-m<x2-1⇔存在x∈[1,e],使m>(4lnx-x2+1)min.
解题策略:存在x∈A,使f(x)≥g(x)成立⇔x∈A,使[f(x)-g(x)]max≥0;存在x∈A,使f(x)≤g(x)成立⇔x∈A,使[f(x)-g(x)]min≤0恒成立.
三、含二元或多元的“任意”与“存在”问题的解法
所以当x∈[0,1]时,f(x)min=f(0)=-1.
根据题意可知存在x∈[1,2],
使得g(x)=x2-2ax+4≤-1,即x2-2ax+5≤0,即成立,
则要使a≥h(x)在x∈[1,2]能成立,只需使a≥h(x)min
解题策略:任意x1∈A存在x2∈B,使f(x1)≥g(x2)成立⇔x1∈A,x2∈B使f(x1)min≥g(x2)min.
“任意”“存在”问题一直是高考中的热点问题,此类问题涉及到函数与导数、不等式与方程等知识,考查了同学们基本计算能力及转化与化归思想、分类讨论的数学思想以及分析问题解决问题的能力。解决此类问题的方法较多,需具体问题具体分析,虽有难度但有规律可循。为此我们要善于观察、善于归纳,把“任意”、“存在”问题转化为我们熟悉的最值问题,就能取得成功。

