课堂教学中“一题多变”的训练策略研究
侯俊玲
摘 要 数学教学不但要教给学生数学知识,还应当培养学生多方面的素质能力。针对数学知识抽象、复杂的特点,通过引导学生进行数学知识的分析、理解,十分有助于发展学生的思维能力。在数学课堂教学中,进行“一题多变”训练,能够让学生从多方面、多角度、多层次去理解数学概念,解决数学问题,发展数学思维。
关键词 课堂教学;一题多变;训练策略
中图分类号:G424.21 文献标识码:A 文章编号:1002-7661(2019)09-0148-01
数学教学主要依托于教材,其中有很多典型的习题、例子可以让学生进行知识的理解、探索。教师在实际的教学过程中,应当对教材中的这些习题、例子加以重视,进行引申、拓展,使它们能够充分为课堂教学服务。同时数学习题形式的多变也有助于吸引学生的好奇心以及学习兴趣,培养起学生探索精神、创新思维、观察能力、分析及解决数学问题的能力。根据数学知识形式多变的特点,教学中教师如果能够有效的利用起“一题多变”教学法,将会极大提升数学教学质量。本文对“一题多变”训练策略进行总结。
一、循序渐进,由浅入深
人们对客观事物的认识都要经历由简单到复杂、由直观到抽象的过程,通过表象逐渐看到本质。在数学课堂教学中,教师也应当遵循学生的知识认识规律,在评估学生知识理解能力、接受能力的基础上,循序渐进进行诱导,让学生通过自己的一步步努力能够不断实现新的突破,体验成功的喜悦,从而越学越有动力。“一题多变”教学法则能实现激发学生数学兴趣的目的。
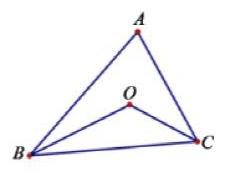
比如:我们在学习了与三角形有关的角的内容之后常会碰到这样一个习题。
例如:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分别平分∠ABC和∠ACB
求:∠BOC的度数
在处理这个习题时,同学们首先想到的就是在△BOC中利用内角和定理来求∠BOC,即:要求∠BOC,就要先求出∠OBC和∠OCB的度数,或求出∠OBC和∠OCB的度数和。学生在解决此问题后之后抛出变式一:将条件改为:∠ABC=45°,∠ACB=65°其它条件不变,求:∠BOC的度数。同样方法学生可以结出结果,然后引导学生猜想猜想得出∠BOC的度数和三角形ABC的哪一个内角有关,有何关系?进而抛出变式二:探究∠BOC和∠A的度数关系。在处理该习题时采用的方法就是循序渐进,由表及里,符合学生认知规律。
二、由此及彼、类比思想
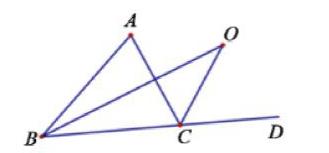
在解决了刚才的那个问题后,可以类比刚才的方法抛出变式进而抛出变式三:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分别平分∠ABC和外角∠ACD。
求:∠BOC的度数
教师引导学生运用类比的思想解决该变式后,让学生类比前面的自己给出组变式题目并尝试解决总结规律。然后水到渠成的出现变式四、五。
变式四:将变式三条件中的∠ABC改为45°,∠ACB=65°其它条件不变。
求:∠BOC的度数
变式五:∠O和∠A的度数关系。解决此问题时,一直类比前面的变式题目进行。
三、变换图形,总结归纳
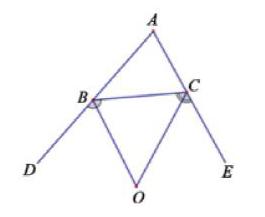
在解决了问题及几个变式后,分析发现该变式题的问题是在例题的基础上将两个内角的平分线所形成的夹角角变为一内角及一外角的平分线所形成的夹角。那么:如果该为两个外角的平分线的夹角会出现什么情况呢?让学生画出图形来,结合图形给出下面的几个变式。
变式六:在△ABC中,∠ACB=60°,∠ABC=50°,BO,CO分别平分外角∠CBD和外角∠BCE。
求:∠BOC的度数
变式七:将变式六条件中的∠ABC改为45°,∠ACB=65°其它条件不变。
求:∠BOC的度数
变式八:探究变式六、七中∠BOC和∠A的度数关系
这样本来一个题目,通过由表及里,由特殊到一般,举一反三、类比运用,得出三个结论即∠O分别等于90°+∠A,∠A和90°—∠A。
总之,“一題多变”教学法能够调动学生思维的灵活性、深入性,从改变图形入手,只要能够抓住图形特点,便能由表及里、举一反三,引导学生更深入的思考数学问题。
参考文献:
[1]章美琼.课堂教学中的“一题多变”策略研究[J].亚太教育,2016(18):43.

