考虑后刀面磨损及过缝冲击的拼接模具铣削力建模与实验研究
岳彩旭, 都建标, 姜 男, 高海宁, 朱 磊, 刘献礼
(哈尔滨理工大学 机械动力工程学院,哈尔滨 150080)
汽车覆盖件具有表面精度要求高、尺寸大等特点,常常作为重要的零部件应用于各类汽车之中。随着汽车行业的快速发展,汽车覆盖件表面日益复杂多样,会导致模具型腔出现大量的凸凹、沟槽等结构,加工时会使型腔受损而降低模具的使用寿命,同时容易出现拉毛拉裂、磨损严重等问题。通常,在铣削加工中为了克服模具设计和加工制造、装配存在的困难,多采用镶块式模件拼接后整体加工。但是在拼接模具铣削加工过程中易出现刀具磨损和过缝冲击现象,导致切削力突变,因此,建立考虑刀具后刀面磨损的拼接模具铣削力预测模型,对拼接模具铣削加工工艺优化具有重要意义。
为了深入刀具磨损及铣削力建模的研究,国内外诸多学者展开了系统研究,Marrtellotti[1]基于运动轨迹的方法建立了铣削力模型,同时引入了瞬时切削厚度模型,为铣削力建模理论研究奠定了基础。之后,Merchant[2]在著名的铣削剪切理论基础上推导了Ernst-Merchant铣削力公式,并进行了实验验证。Nakayama等[3]提出了铣刀近似刃线方程,且通过微元铣削力的方法建立了铣削力模型,并对铣削力模型进行了实验验证。冯志勇等[4]根据铣刀数学模型建立了与瞬时切厚有关的非线性函数,进而得到了铣刀的铣削力模型,并通过实验对所建铣削力模型进行了验证。Jeong等[5]建立了考虑刀具变形和刀具偏心影响下的瞬时切屑厚度模型,进而通过瞬时切削力系数得到了球头铣刀的机械式切削力模型,并通过实验进行了验证。Tsai等[6]针对球头刀几何特性提出了一种新的表达方法,主要是将球头刀的刃线看作一个球面和倾斜面的交线,进而通过矩阵变换得到了切削刃的实际位置,对之后的铣削力建模研究具有一定的理论指导意义。Lim等[7]在铣削力的预测中,建立了考虑刀具偏离的柔性力模型和刚性力模型,并且通过实验验证了模型的准确性。吴俊谦[8]针对单一硬度模具及多硬度拼接模具进行了铣削力建模研究,并通过单一硬度模具及多硬度拼接模具的铣削实验验证了所建模型的准确性,同时,研究结果表明过缝处的铣削力峰值与加工倾角呈正相关。王扬渝[9]通过有限元分析与实验研究相结合的方法对拼接模具铣削过程中铣削力及铣削振动进行了深入研究,并通过实验验证了模型的准确性。岳彩旭等[10]利用球头铣刀对不同硬度淬硬钢拼接模具进行了铣削实验,揭示了切削深度、切削速度、进给速度及刀具铣削方向对拼接处铣削力突变的影响规律;并得到了切削参数的主次影响规律和最优参数组合。刘战强等[11]对CBN刀具、陶瓷刀具及金刚石等高速切削刀具的磨损形成机理及磨损状态进行了综评,并对刀具磨损寿命的影响因素进行了分析,对实际生产加工具有很好的指导意义。Li等[12]对镍基高温合金铣削过程中的刀具磨损状态进行了研究,根据刀具磨损量增加切削力随之增加的规律,对刀具磨损状态进行了识别和检测。Tansel等[13]对槽铣过程中刀具磨损状态进行了研究,主要通过获取进给方向的铣削力,并使用神经网络的方法对提取的特征值进行刀具磨损状态判断。李锡文等[14]建立了考虑铣刀后刀面磨损面积的铣削力模型,并通过铣削实验验证了模型的正确性。Choudhury等[15]对铣削过程中的刀具磨损状态进行了研究,通过平均切削力系数与刀具后刀面磨损的关系提出了一种刀具磨损评估方法。
国内外学者大多数针对于单一硬度下的铣削力建模或未考虑刀具磨损的拼接模具铣削力建模,而对考虑刀具磨损的拼接模具铣削力建模相对较少,故对考虑刀具磨损的拼接模具铣削力建模研究具有重要意义。本文考虑了过缝冲击及刀具磨损等因素,结合剪切力模型、摩擦效应力模型与冲击力模型得到了考虑后刀面磨损的拼接过缝处铣削力模型。最后通过实验验证了该铣削力建模方法的有效性。
1 拼接处冲击力求解
1.1 法向接触力模型
球头铣刀过拼接缝切向另一硬度材料时,刀具与工件成一定角度接触,为此可以认为刀-工接触模型为单自由度斜体碰撞模型。接触碰撞过程可以看作是连续动力学问题,其碰撞过程可以等效成弹簧阻尼模型[16]。法向接触力的求解公式可以表示为
(1)

模型中将球头刀理解为圆柱体。在Hertz弹性接触理论中,规定如果研究体形状简单时,可以将其由材料的杨氏模量、泊松比计算出接触刚度系数与指数,如式(2)所示

(2)
其中,R和E分别为
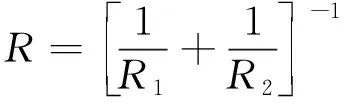
(3)

(4)
式中:E1和E2分别为两个碰撞物体材料的杨氏模量;R1和R2分别为两个碰撞物体在碰撞点的接触半径;μ1和μ2分别为两个物体材料的泊松比。
法向接触力模型适用于碰撞物体接触的整个过程中,选择一个合理的模型和计算公式则是处理和解决接触碰撞问题的关键。文献[17]提出了一种如下形式的迟滞阻尼模型
D=μδe
(5)
其中,μ为迟滞阻尼因子,计算公式为

(6)

1.2 切向接触力模型
在接触碰撞的过程中两个接触物体有相对滑动,切向方向会受到摩擦力的作用,斜碰撞中经常出现切向摩擦力。本文中考虑的摩擦力是基于Coulomb摩擦力。其主旨思想为:摩擦力与法向载荷成正比,且与运动方向相反,与接触面积无关,得到切向接触力模型为
Fs=μsFn
(7)
式中,μs为迟滞阻尼因子。
2 剪切力模型
2.1 微元铣削力模型
图1所示为球头刀铣削拼接模具加工过程示意图。工件坐标系为O-XYZ。刀具坐标系O′-XcYcZc建立在刀具底部中心O′处,轴Xc、Yc分别平行于X和Y,轴Zc与刀具轴线重合,f为进给矢量,起点与O′重合。Fs和Fn只在XY平面内。

图1 拼接模具铣削过程示意图
在球头刀切削刃上选取一点P,在铣削加工过程中P点是沿着一条摆线运动,其方向与刀具进给方向相同。当球头刀切削拼接处时,切削刃同时切削两种不同硬度的材料,这时将切削两种不同材料的切削刃离散为切削刃微元P1和P2。球头刀在拼接模具不同硬度处铣削力的微元法建模,如图2所示。
基于铣削力模型和切削刃离散单元化的方法,过拼接缝处切削刃上离散的任意微元力。微元切向力、径向力和轴向力分别为

(8)
式中:dFt1和dFt2分别为第一种材料硬度和第二种材料硬度下的微元切向力;dFr1和dFr2分别为第一种材料硬度和第二种材料硬度下的微元径向力;dFa1和dFa2别为第一种材料硬度和第二种材料硬度下的微元轴向力。
P1在第一硬度区的微元铣削力为
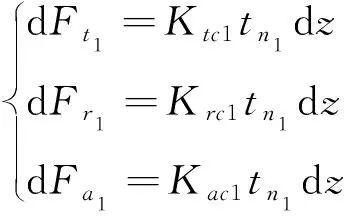
(9)
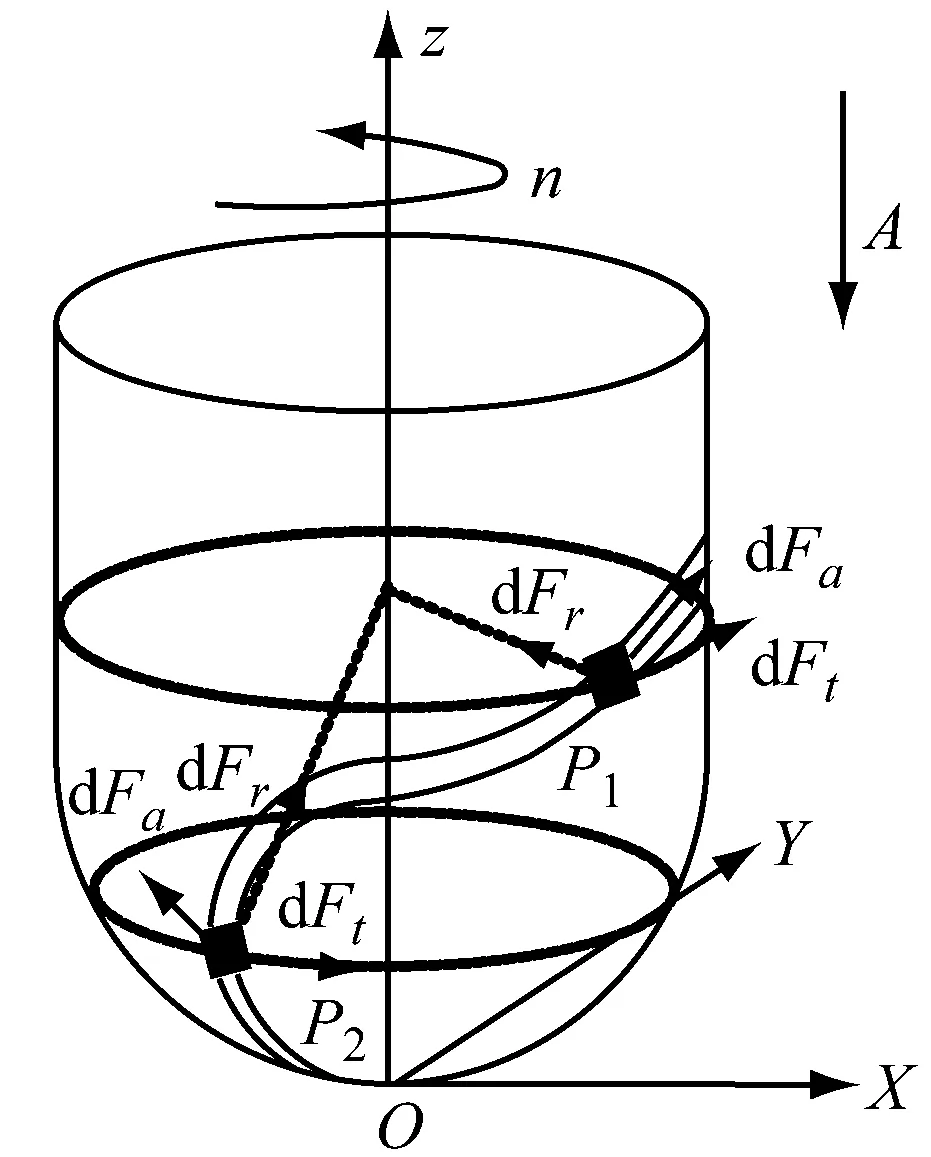

图2 拼接模具不同硬度处铣削力微元法建模
P2在第二硬度区的微元铣削力为

(10)
式中:Ktc1、Krc1和Kac1分别为第一硬度区的切向铣削力系数、径向铣削力系数和轴向铣削力系数;Ktc2、Krc2和Kac2分别为第二硬度区的切向铣削力系数、径向铣削力系数和轴向铣削力系数;tn1为P1点的瞬时切削厚度;tn2为P2点的瞬时切削厚度。
将微元力转换为XYZ坐标系统,其结果为

(11)
式中:θj为旋转角度。
2.2 切削区域与切削厚度的计算
在模型中引入时间变量t,t=0时为球头刀刀齿刚开始切削拼接位置,拼接过缝处切削厚度划分如图3所示。球头刀切入工件时所对应切入部分的最大半径为

(12)
从t=0时开始,球头刀切削拼接过缝处的总切削时间为

(13)
当0≤t≤tg时,球头刀处于切削过缝区域。
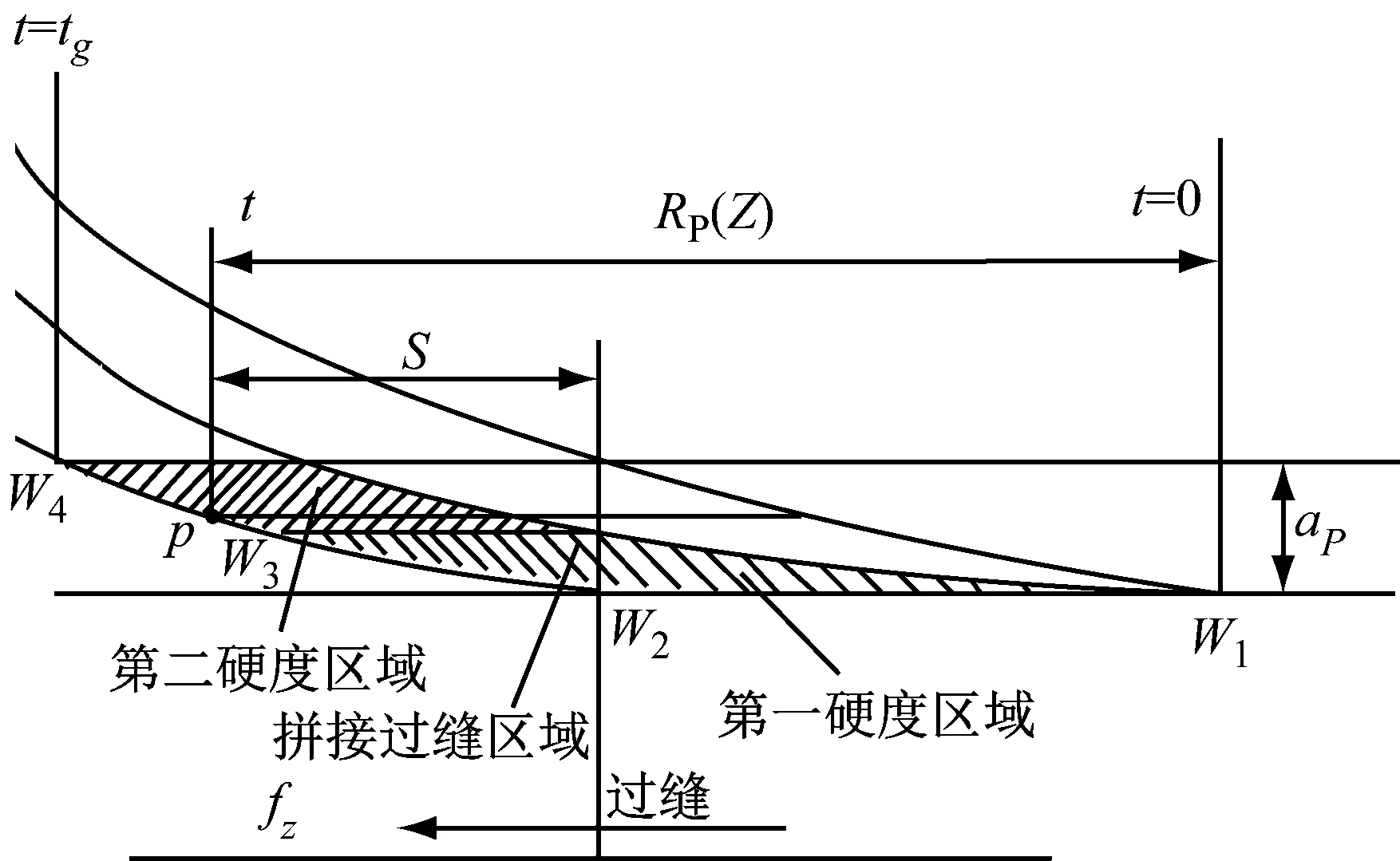
图3 拼接过缝处切削厚度划分
设在t时刻球头刀切入第二硬度区时最远距离为L,所以前一刀齿距离拼接缝的最大距离为L-fz。本文建立的瞬时切削厚度模型一共分为第一硬度区域(60 HRC)、第二硬度区域(50 HRC)和拼接过缝区域三个区域,其中L=f·t,f为进给速度,fz为每齿进给量,φ为轴向位置角,R为球头刀半径。
球头刀切削刃上P点离切削圆中心轴线的P点的半径Rp为
Rp=Rsinφ
(14)
点P在进给方向上距切削圆中心轴线的半径Rp(z)为
Rp(z)=Rpsinθj
(15)
则P点和拼接过缝处的间距S

(16)
当S≤0,则球头刀P点处在第一硬度区中。
则切削刃上P的瞬时切削厚度T只在第一硬度区进行求解
tn1=fz·sinθj·sinφ
(17)
当S>0,则球头刀P点处在第二硬度区中。
设当前刀齿的瞬时切削厚度T,则球头刀前一刀齿与拼接过缝的间距为
S-1=S-T·sinφ
(18)
当S-1≥0,则在球头刀切削刃上P的瞬时切削厚度T只在第二硬度区
tn2=fz·sinθj·sinφ
(19)
当S-1<0,则球头刀切削刃上的P点的瞬时切削厚度同时切削第一硬度区和第二硬度区,分别在两个硬度区选取球头刀切削刃上的两个微元点P1和P2,可以得到tn1和tn2
tn1=fz·sinθj·sinφ-S/sinφ
(20)
tn2=S/sinφ
(21)
2.3 参与切削的切削刃极限位置
选取临界点W1、W2、W3和W4,它们分别在球头刀切削刃上第一硬度区、第二硬度区以及拼接区的相交位置;则W1和W4处的位置角为
φ1=0
(22)
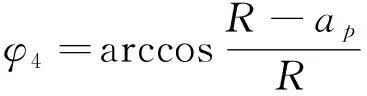
(23)
在W2处,切削刃微元W2距离拼接过缝的距离为0,所以当S=0时,可以确定φ2的值。
(24)
而在临界点W3处,可以知道在球头刀前一刀齿和拼接过缝之间的间距为0。所以S-1=S-T·sinφ=0,即S=T·sinφ。通过下式可以求得φ3。
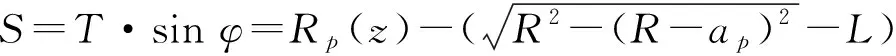
(25)
3 摩擦效应力模型
摩擦效应力模型只在XY平面建立。摩擦效应力是由球头刀后刀面和工件表面的挤压和摩擦引起的。因此,摩擦效应力与球头刀后刀面磨损有关和未变形切削厚度无关[18]。
切向摩擦力和径向压力可以表示为
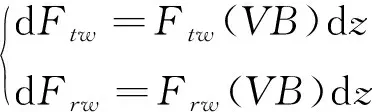
(26)
式中:dFtw和dFrw分别为切向摩擦力和径向压力;Ftw(VB)和Frw(VB)分别是后刀面单位长度的摩擦力和压力,它们都与刀具磨损有关。
同样,将微元力转换到XYZ坐标系统,其结果为

(27)
球头铣刀后刀面单位长度的摩擦力和压力可以表示为
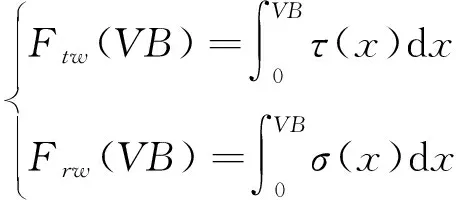
(28)
式中:τ(x)为球头刀后刀面切应力;σ(x)为球头刀后刀面正应力,x为切削刃长度;VB为球头刀后刀面的磨损宽度。
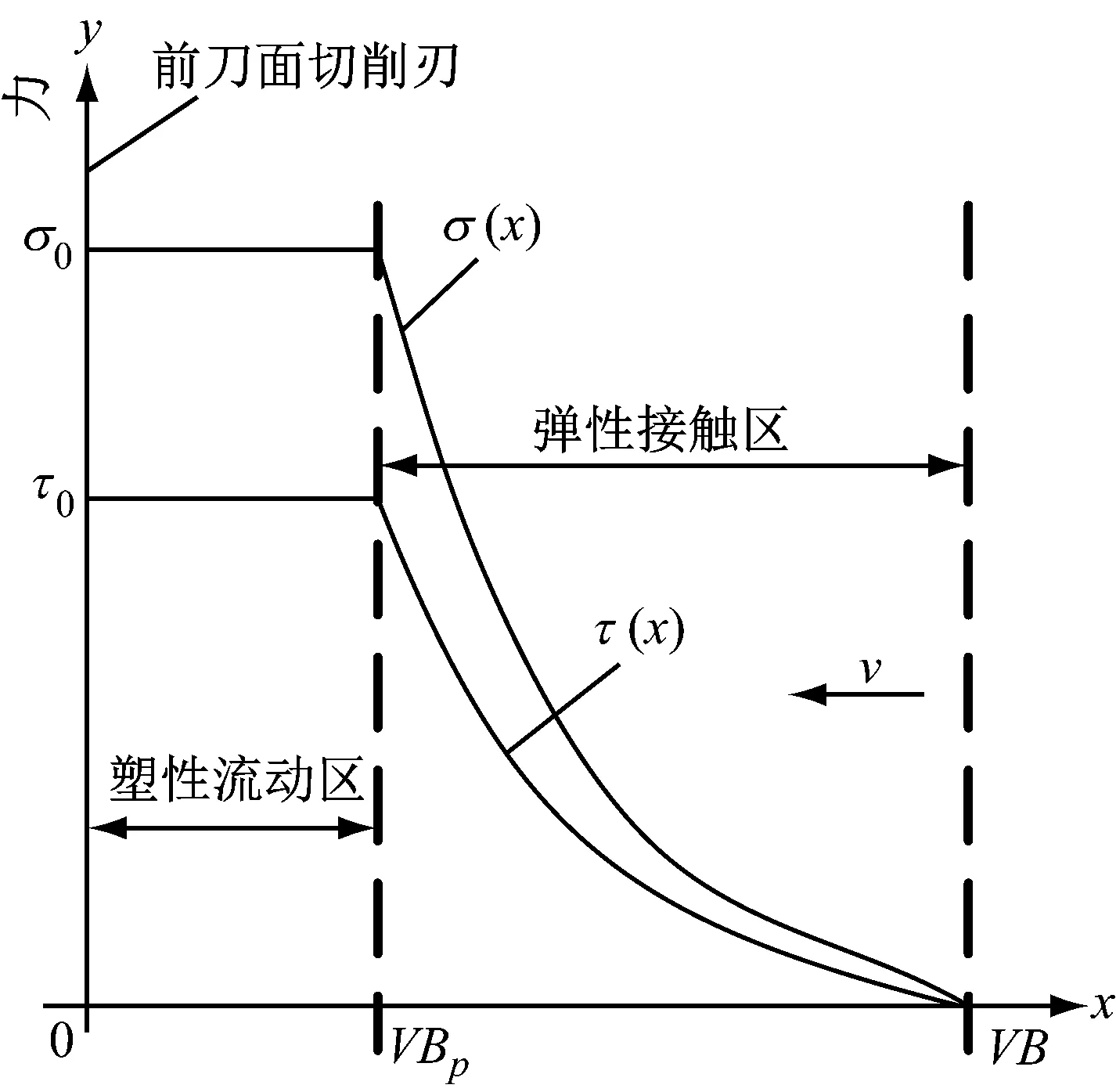
后刀面磨损和工件的接触区域分为塑性流动区和弹性接触区,研究主要关于后刀面磨损和工件的接触,两者基于材料流动和滑移[19]。本文主要研究球头刀后刀面的塑性流动区和接触区两个区域。如图4所示为刀具后刀面磨损应力分布,从图中可以看出切向力和法向力在塑性流动区是恒定的,分别为τ0和σ0;而在弹性接触区呈现二次分布。
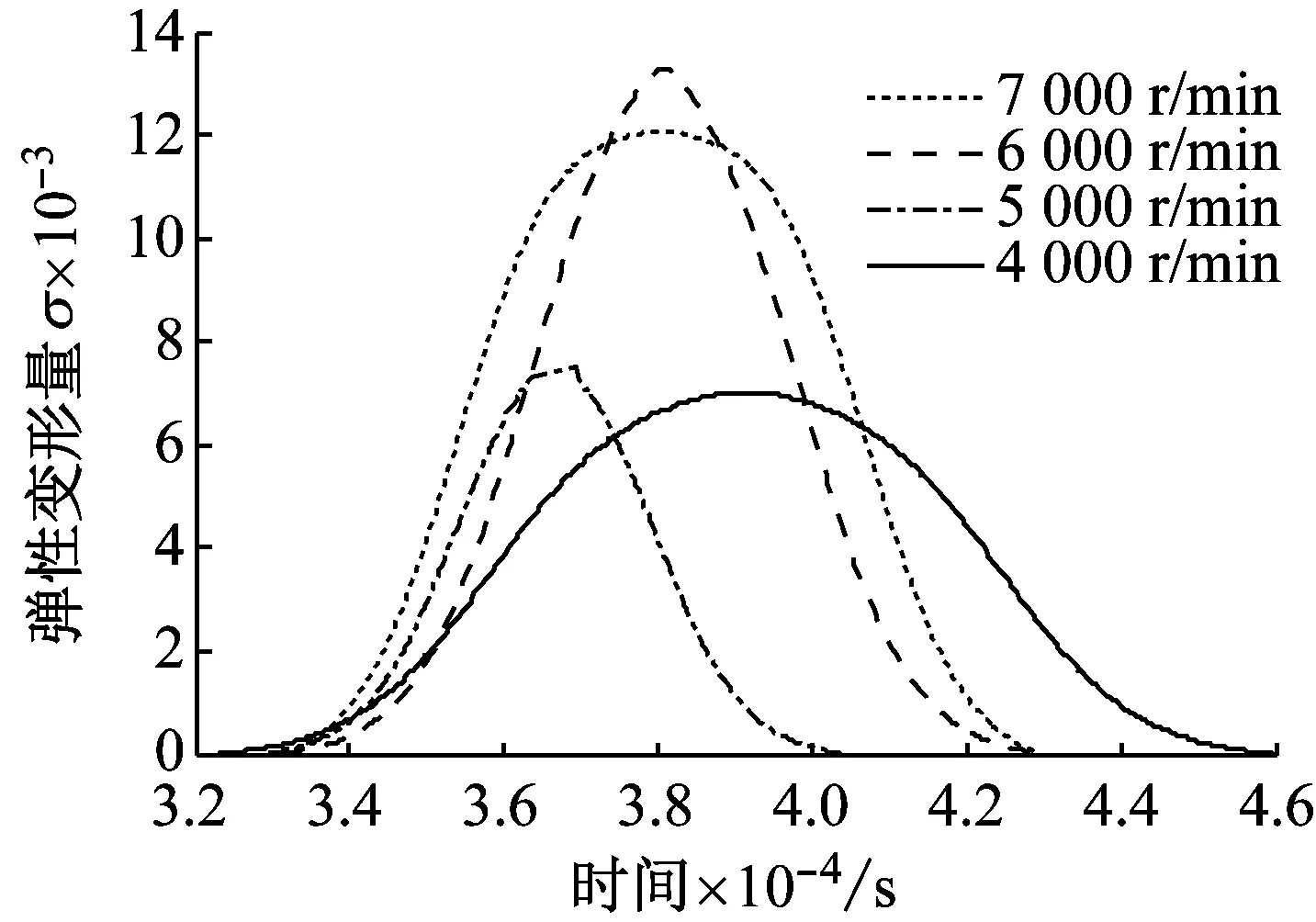
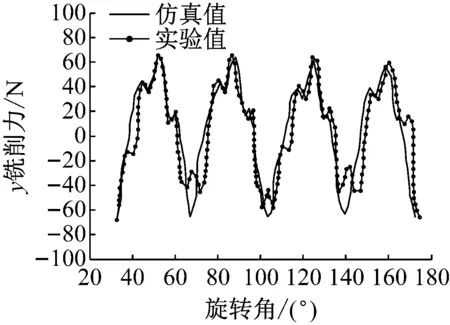
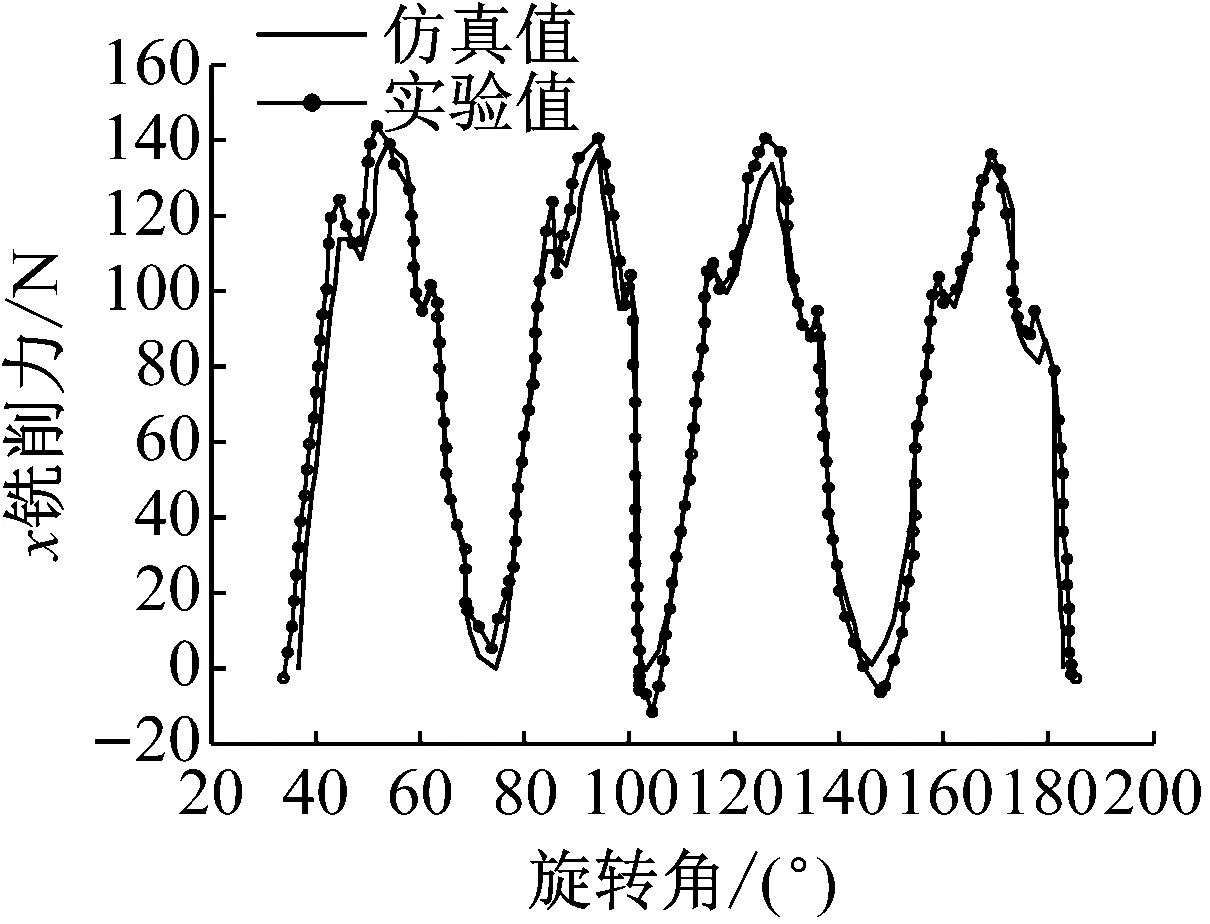
当0 (29) 图4 刀具后刀面磨损应力分布 当VBp (30) VBp是塑性流动区和弹性接触区的边界。当刀具磨损到达一定的量时,弹性接触区的宽度保持恒定,塑性流动区的宽度随着刀具后刀面磨损的增加而增大。可以表示为 当VB VBp=0 (31) 当VB≥VB*时, VBp=VB-VB* (32) 式中:VB*为弹性接触区的宽度。 通过将式(29)和(31)代入到式(28)中,我们可以得到球头刀后刀面单位长度的摩擦力和压力 当VB (33) 当VB≥VB*时, (34) 通过对刀-工切触区域内进行球头刀有效切削刃段的计算,然后可以求解x和y两个方向的铣削力合力。所以,在拼接过缝处球头刀总的切削力为 (35) 其中, Ftimpact=Fn·cosθgf Frimpact=Fn·sinθgf+Fs 式中:Nf为刀具齿数,φ1和φ4为最小和最大轴向位置角,θst为切入角,θex为切出角,θgf为过缝处的切削角度。 在拼接缝处二次切入模型应用斜碰撞模型的前提是刀具-工件发生的是弹性变形,为得到不同主轴转速下刀-工碰撞的弹性变形量δ,本文通过改变加载气压,在不同子弹(撞击杆)加载速度下进行了SHPB冲击实验,当枪膛内的子弹以不同速度撞击输入杆时,所产生的压力波先后被应变片所记录,经数据处理系统处理,即可得到不同主轴转速下刀-工碰撞的弹性变形量δ,进而得到过缝处刀具所受到的冲击力。实验设备如图5所示。 图5 SHPB实验设备 霍普金森杆冲击实验测试装置为ARCHIMEDES ALT1000,系统瞬态最高采样速率1 MHz,具备自动测试控制和数据波形分析功能。测试试件分别为50 HRC和60 HRC的淬硬钢,试件几何尺寸均为长度5 mm、直径5 mm的圆柱体。图6为室温条件且在不同主轴转速下获得的不同硬度淬硬钢材料的真实应力-应变曲线。两图中每一条曲线的材料弹性变形阶段即为碰撞模型弹性变形量δ。对比图中的四条曲线,可以得到:在弹性变形阶段,随着主轴转速的增加,相同应力下工件的弹性变形量(真实应变)逐渐增大,此过程应力应变为非线性关系。得到了在不同主轴转速下不同硬度淬硬钢材料的真实弹性应变曲线,如图7所示。 由刀-工接触关系可知:R1=4.8 mm;R2=∞;工件弹性模量为180 GPa,泊松比为0.3;刀具弹性模量为600 GPa,泊松比为0.2。进而得到刚度系数K=1.51e5,e=1.5。阻尼系数和恢复系数通过实验来获得[20],经查可得u=0.15。 (a) 硬度HRC60应力-应变曲线 (b) 硬度HRC50应力-应变曲线 (a) 弹性应变曲线60 HRC (b) 弹性应变曲线50 HRC 铣削力实验所采用的数控机床为大连机床集团有限责任公司生产的三轴数控铣床,实验使用的刀具为厦门金鹭公司生产的整体式球头铣刀,齿数为2,刀具直径为10 mm,螺旋角为30°,实验工件是由50 HRC和60 HRC的淬硬钢模具拼接而成,铣削力的采集选用瑞士先进的旋转测力平台,拼接模具钢的实验加工现场如图8所示。 图8 VDL-1000E三轴加工中心及采集设备 本文铣削力系数法是在保持其他铣削参数不变条件下,通过改变每齿进给量来获得各组铣削力变化趋势,再利用最小二乘曲线拟合法获得瞬时铣削力系数,第一硬度区的切向铣削力系数Ktc1=-2 584.2、径向铣削力系数Krc1=-1 656.7;第二硬度区的切向铣削力系数Ktc2=-1 842.2、径向铣削力系数Krc2=-956.1。 实验参数设置为主轴转速4 000 r/min,进给速度1 200 mm/min,切深0.2 mm,切宽0.25 mm。实验每相隔50 min对球头刀后刀面的磨损量进行测量,当达到实验设定的磨损量时进行铣削力实验。刀具磨损测量装置采用基恩士公司生产的超景深显微镜。球头刀后刀面各阶段的磨损状态如图9所示。 图9 各阶段磨损状态 本文主要针对拼接过缝区进行研究,选择过缝处的固定2个齿周期进行比对。由图10~图13不同刀具磨损量下铣削力仿真结果与实验结果对比图可知。随着球头刀后刀面磨损量的增加,x和y方向的铣削力都逐渐增加,这说明球头刀后刀面的磨损状况对于铣削加工中的铣削力影响较大。 (a)Fx仿真与实验结果 (b)Fy仿真与实验结果 图10VB=0 mm时铣削力仿真与实验对比 Fig.10 Simulation and experimental comparison of milling force inVB=0 mm (a) Fx仿真与实验结果 (a) Fx仿真与实验结果 (a) Fx仿真与实验结果 从图10~图13中可以明显看出,在x和y方向存在着明显的切入冲击力,当后刀面磨损量一定时,在每一个波形的上升段和下降段都有二次冲击的过程,这证明了铣削拼接处存在冲击力,冲击力的幅值低于铣削过程中的最大铣削力,冲击力随着切削时间而逐渐减小,这是因为随着切削时间的进行,切削刀具与工件碰撞的接触点所在圆半径在逐渐减小,并且接触点空间位置角随切削时间逐渐减小;当后刀面磨损量逐渐增加时,冲击力随之增加,这说明球头刀后刀面的磨损状况对于铣削加工中的冲击力影响很大。x和y方向铣削力仿真结果与实验吻合程度很好,其中x和y方向的冲击力最大误差为14.45%和15.26%,这主要是由于机床振动、仪器精度以及主轴径向跳动等因素导致。但总体来说仿真结果在数量级和变化趋势上基本和实验结果相贴合,证明所建立的模型是准确的。 针对汽车覆盖件拼接模具铣削过程中刀具易磨损的问题,建立了考虑刀具后刀面磨损的拼接模具铣削力预测模型,并通过铣削实验进行了验证。得到以下结论: (1) 本文基于球头刀前刀面剪切效应和后刀面摩擦效应,建立了考虑后刀面磨损的拼接模具铣削力模型,同时模型中考虑了过缝处产生的冲击力,引入了单自由度斜体碰撞模型。 (2) 实验结果与仿真结果对比可知,随着球头刀后刀面磨损量的增加,x和y方向的铣削力都逐渐增加,过缝处冲击力大小也与刀具磨损状态呈现正相关。 (3) 当刀具磨损一定时,过缝处的冲击力随着时间而逐渐减小,这是因为随着切削时间的进行,刀具和工件碰撞的碰撞点所在圆半径在逐渐减小,并且接触点空间位置角随时间逐渐减小。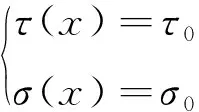
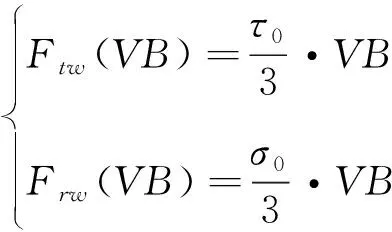

4 已磨损球头刀在过缝处的总铣削力
5 实验与分析
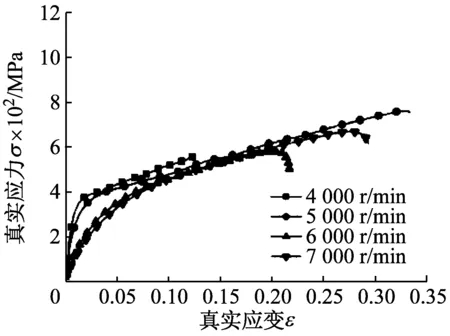
5.1 SHPB冲击实验求解碰撞物体变形量



5.2 拼接淬硬钢铣削力实验

5.3 实验结果分析




6 结 论

