移动的隧道轴向激励作用下两相多孔介质动力反应
包汉营, 陈文化
(北京交通大学 土木建筑工程学院, 北京 100044)
城市地下轨道交通的迅猛发展,缓解了路面交通的拥堵状况,同时也产生了许多环境振动与噪声等问题。对于这一热点问题的研究主要包括两个方面:一是地铁列车与轨道系统的研究;二是地铁振动在地基中的传播及其对地面建筑影响的研究。
针对振动的传播及其影响的研究主要有以下内容:① 单相均质土体在内部移动荷载作用下的动力响应研究。该方向的研究将土体视为单相均匀介质,根据是否考虑隧道结构,振动荷载的形式又包括埋置移动荷载和隧道内部移动荷载两种类型,研究方法主要有理论解析法[1-2]和有限元法[3-5];② 两相多孔均匀介质在内部移动荷载作用下的动力响应研究。考虑到富水(地区隧道往往处于地下水位以下,因此这一阶段的研究将土体视为饱和土体,用Biot饱和多孔介质模型来模拟地基土,振动荷载的形式包括完全对称式[6-7]和非对称式[8-10],Lu等利用波函数展开法分别研究了无衬砌隧道和衬砌隧道内部移动环形荷载作用下全空间饱和土体的动力响应问题;曾晨等分别采用有限元法和Biot饱和多孔介质理论等研究了地铁列车荷载引起的隧道-饱和土体的动力响应问题;③ 移动荷载作用下分层介质的动力响应研究。该方向的研究对象包括单相分层介质[11-12]和两相多孔分层介质[13-14],研究方法主要为数值方法和半解析-半数值的方法。Sheng等采用离散波数虚拟力法、薄层法等研究了内部移动荷载作用下单相层状半空间的动力响应,胡安峰等采用传递反射矩阵法、格林函数法等研究了成层饱和地基在移动荷载作用下的动力响应,并讨论了荷载移动速度、荷载频率等因素对动力响应的影响。
地铁列车在进出站以及紧急制动过程中会产生沿隧道轴向的激励作用,这种沿行驶方向的激励作用是引起隧道和周围介质振动的重要因素之一。目前针对沿列车行驶方向激振力所产生的动力问题的研究,主要集中在普通铁路中列车-高架桥梁动力响应分析[15],以及地铁地面线路中轴向激励对地铁车站的影响等[16],对于城市地下轨道交通中,移动的隧道轴向激振力作用下半空间饱和土体动力响应的研究相对较少。本文利用波函数展开法、镜像原理、傅里叶变换法等,推导了频域内隧道轴向激励作用下饱和土体动力响应的解析解,并给出了饱和土体临界速度的经验公式;通过快速傅里叶逆变换得到了时-空域内饱和土体的动力响应,并研究了激振力移动速度、土体剪切模量、隧道埋深、角度、孔隙率等对饱和土体动力响应的影响,研究成果对探究地铁隧道振动的响应规律以及减振降噪方面有一定的参考价值。
1 轴向激励作用下两相多孔介质动力响应求解
1.1 轴向激励作用下两相多孔介质动力分析模型
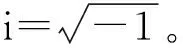

图1 移动的隧道轴向激励作用下饱和土体分析模型
1.2 两相多孔介质振动控制方程及求解
将土体视为饱和多孔弹性介质,不计体力,由Biot饱和土理论[17],隧道外围饱和土体及孔隙水的本构方程和运动方程为
σij=2μεij+λδije-αδijp
(1)
p=-αMe+Mϑ
(2)

(3)
(4)
式中:σij、εij(i,j=1、2、3)为饱和土体应力张量和应变张量;p为孔隙水压力;δij为克罗奈克符号;e、ϑ分别为土体骨架体积应变和单位体积内孔隙流体改变量,e=ui,i,ϑ=-wi,i;ui、wi(i=1、2、3)分别为土体骨架位移和孔隙水的渗透位移分量;λ、μ为土体的拉梅常数;α、M为表征土颗粒和流体压缩性的Biot系数;ρb、ρf分别为饱和土体密度和孔隙水密度,ρb=(1-ne)ρs+neρf,ρs为土体骨架密度;ne为土体的孔隙率;m=a∞ρf/ne,a∞为孔隙流体弯曲系数;η为孔隙流体黏性系数;k为孔隙流体动力渗透系数。
分别取隧道半径r0,土体拉梅常数λ和孔隙水密度ρf为特征尺度,引入以下无量纲变量,对式(3)、(4)进行无量纲化处理
其中X表示与r0有相同量纲的变量,如ui、wi、r、H等。将以上无量纲变量代入式(3)、(4)即可将运动方程变为无量纲运动方程,为简化表达方式,后续公式中的无量纲变量将省略上标“*”。
在求解控制方程时,需对控制方程进行傅里叶正、逆变换,本文采用以下傅里叶变换对
(5)
(6)
式中:Ω表示时间或空间坐标变量;ζ表示频率或波数。
为求解式(1)~式(4),用Helmholtz势函数表示位移
(7)
(8)
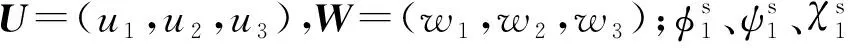
将式(7)、(8)代入式(3)、(4),并对饱和土体运动方程进行时域到频域的傅里叶变换得
(9)
(10)

对式(9)、(10)进行空间坐标z1到波数ξ的傅里叶变换得
(11)
(12)
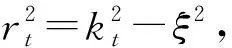
(13)
(14)

针对轴向激振力引起的介质波动特性,采用如图2所示的镜像原理,以自由表面为镜面对称出虚拟振源。根据镜像原理可得
(15)
(16)
由此可得总波场为
(17)
(18)

图2 镜像原理
由Graf加法公式及贝塞尔函数的相关性质可得
(19)
其中
将式(19)代入式(17)、(18)得

(20)

(21)
参考文献[2,6-7]中的处理方式,隧道内部边界条件为
(22)
对式(22)进行t到ω,z1到ξ的双重傅里叶变换得
(23)
由以上各式及边界条件可得
(24)
其中
L1=
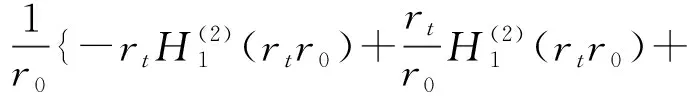

柱坐标系下土体骨架位移及应力为
(25a)
(25b)
后续推导以位移响应为例,对式(2)、(25a)进行t到ω,z1到ξ的双重傅里叶变换得
(26)
(27)

将式(20)代入式(26)得
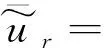
(28)

(29)

(30)
对式(28)~式(30)进行ξ到z1的傅里叶逆变换,得到频域内位移和孔隙水压力的解答
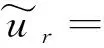
(31)
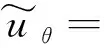
(32)

(33)
式中:L1、L2、L3、rt中的ξ=-ω/v。
2 动力响应及参数分析
2.1 确定土体临界速度vcr
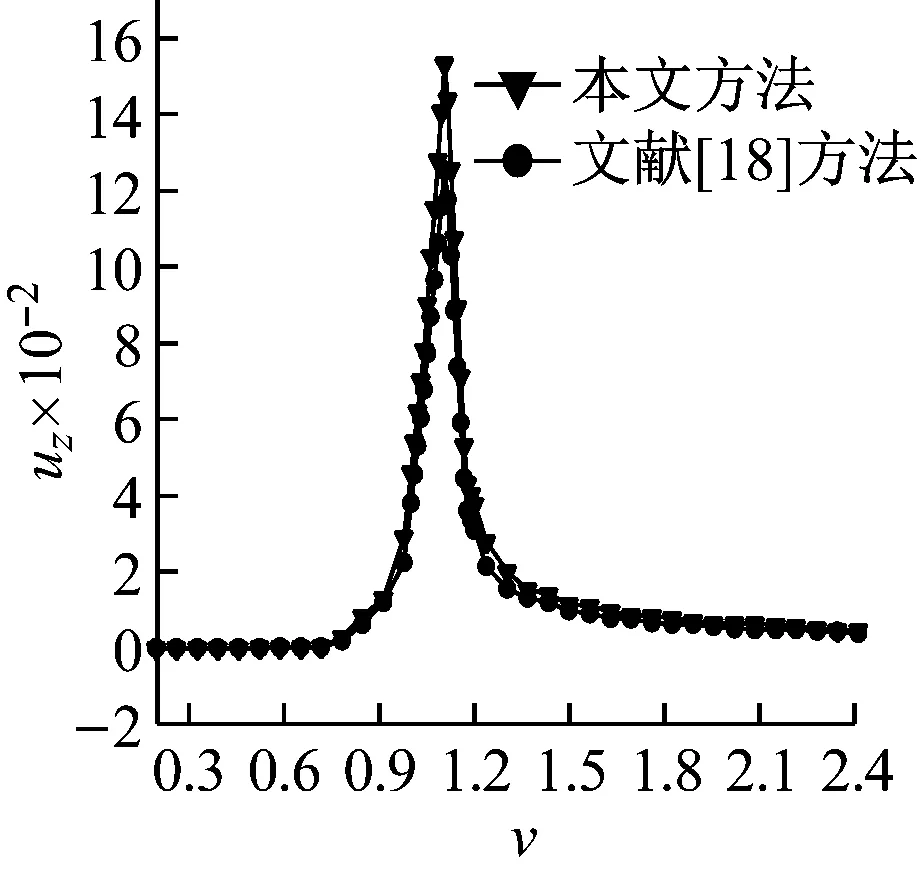
由式(31)~式(33)计算r1=1.5r0处饱和土体的动力响应,图3~图5中(a)图为ω=10、(b)图为ω=20时的动力响应,横坐标为无量纲速度。其中文献[18]采用的是最小二乘法处理自由表面边界,虽然文献[18]分析的是单相介质问题,但是其处理自由表面边界的方法可以应用于两相介质当中,图3~图5即为两种不同边界处理方法计算得到的两相饱和介质的动力响应。由图可以看出,两种方法的计算结果能够较好的吻合,且不同角频率下的动力响应随着激振力移

(a)

(a)
(a)

vcr=a(μ/λ)bv0
(34)
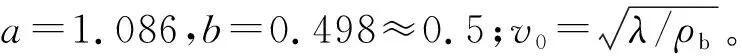
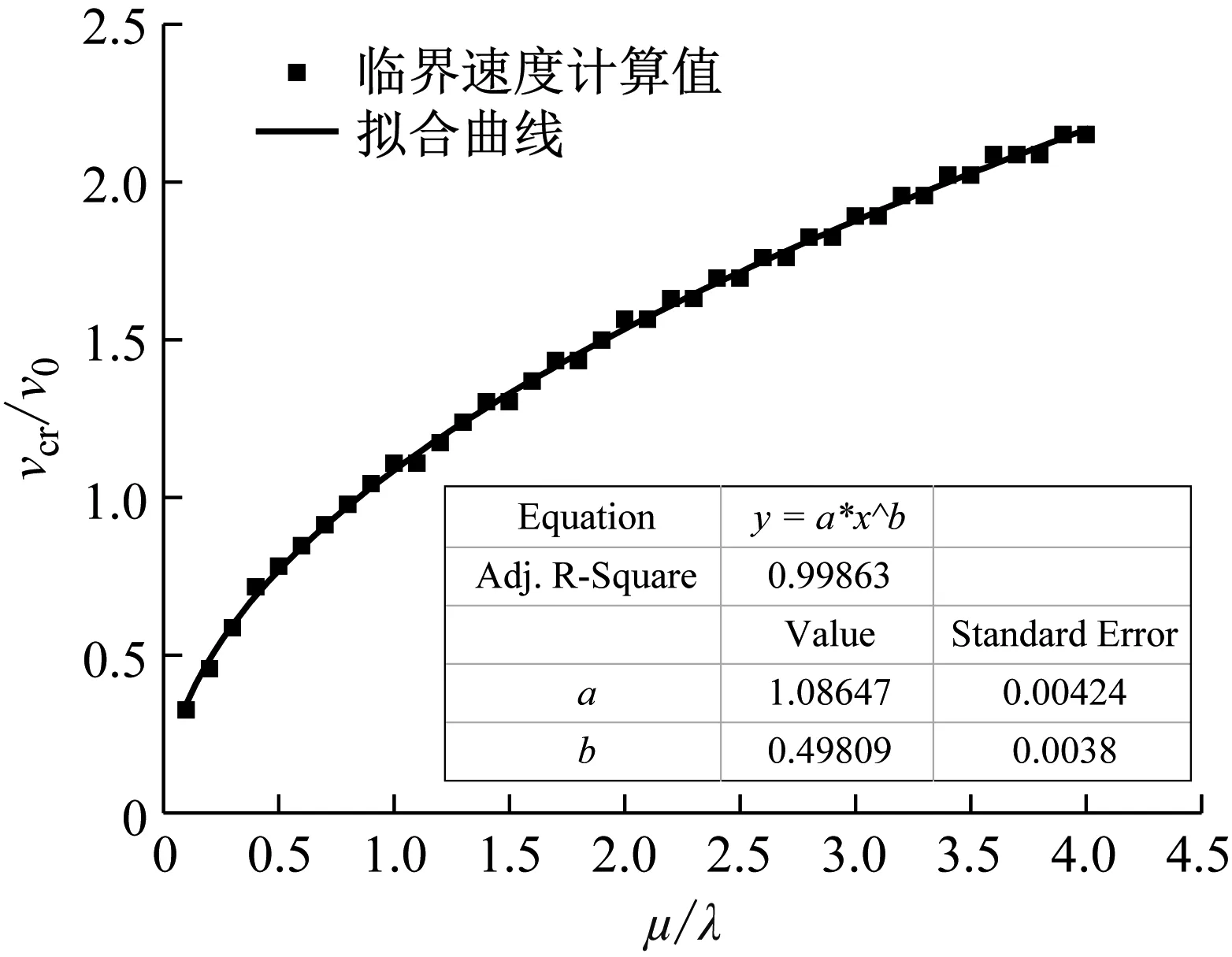
图6 剪切模量对土体临界速度的影响
(35)
由式(35)及图3~图5可以看出移动的隧道轴向常激励作用下,饱和土体的临界速度仅与土体的剪切模量以及密度有关,与隧道埋深、响应频率等因素无关,同时,临界速度的数值接近于1.1倍的剪切波速。后续内容将分别讨论以下两种工况,工况一:速度小于临界速度,取0.65v0;工况二:速度大于临界速度,取2.60v0。
2.2 剪切模量对动力响应的影响
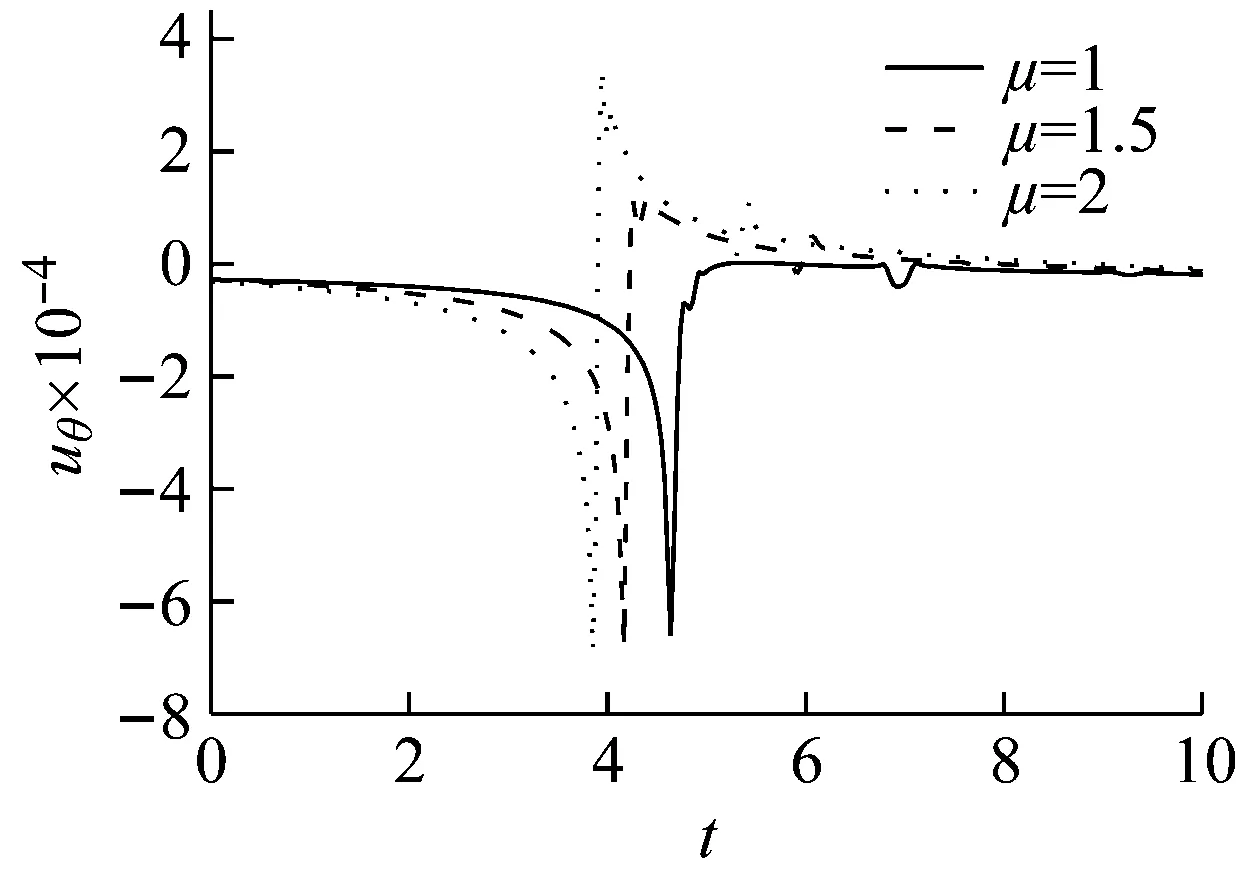
土体的无量纲剪切模量分别取1.0、1.5、和2.0,其它基本参数同2.1节,图7~图9分别为时域内剪切模量对土体径向位移、环向位移以及轴向位移的影响曲线。
由图7~图9可以看出:工况一中各动力响应随着μ的增大而减小,但达到最大振幅的时间不随μ的增大而变化;工况二中各动力响应随着μ的增大而增大,uθ达到最大值的时间随着μ的增大而减小;除径向位移外,对于同一响应,μ取相同数值时,工况一的响应幅值明显小于工况二的响应幅值,达到幅值的时间明显大于工况二的时间。
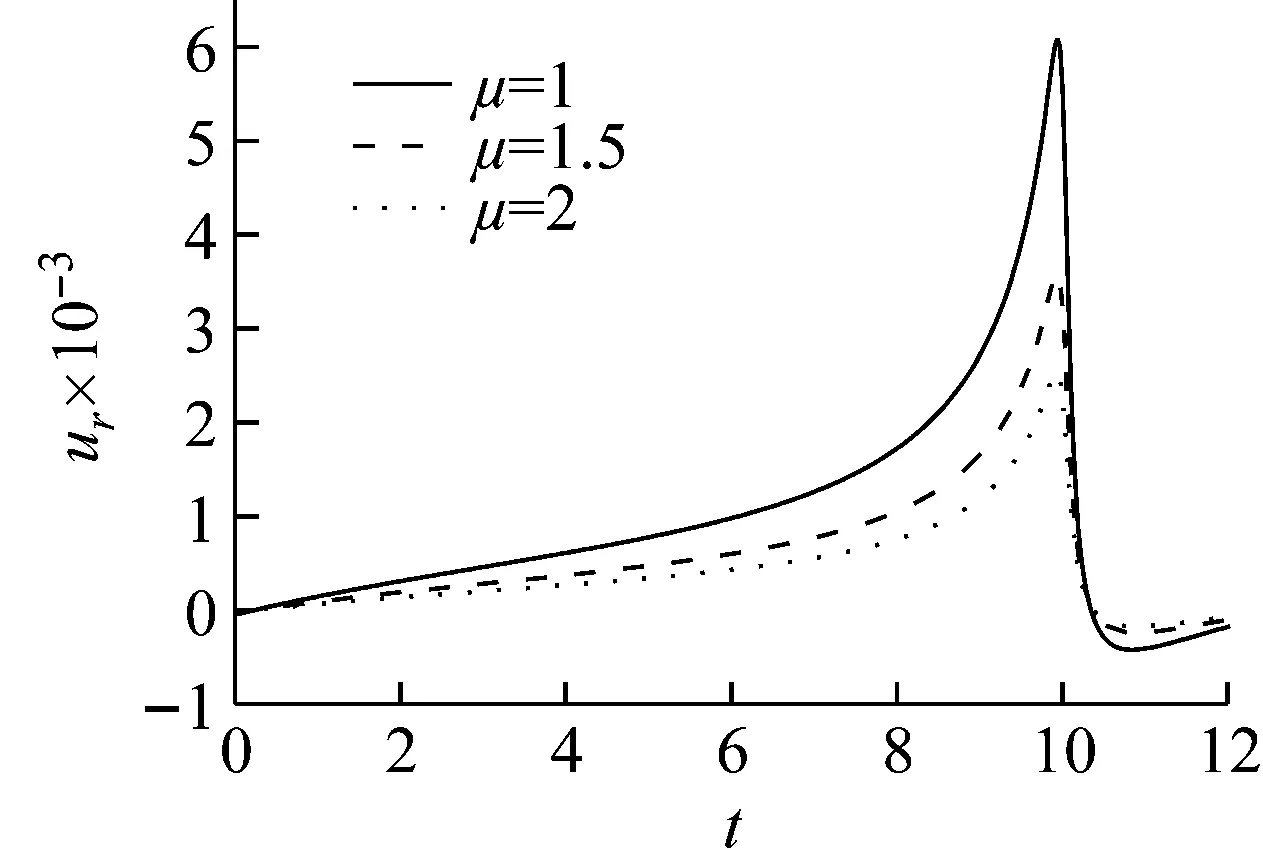
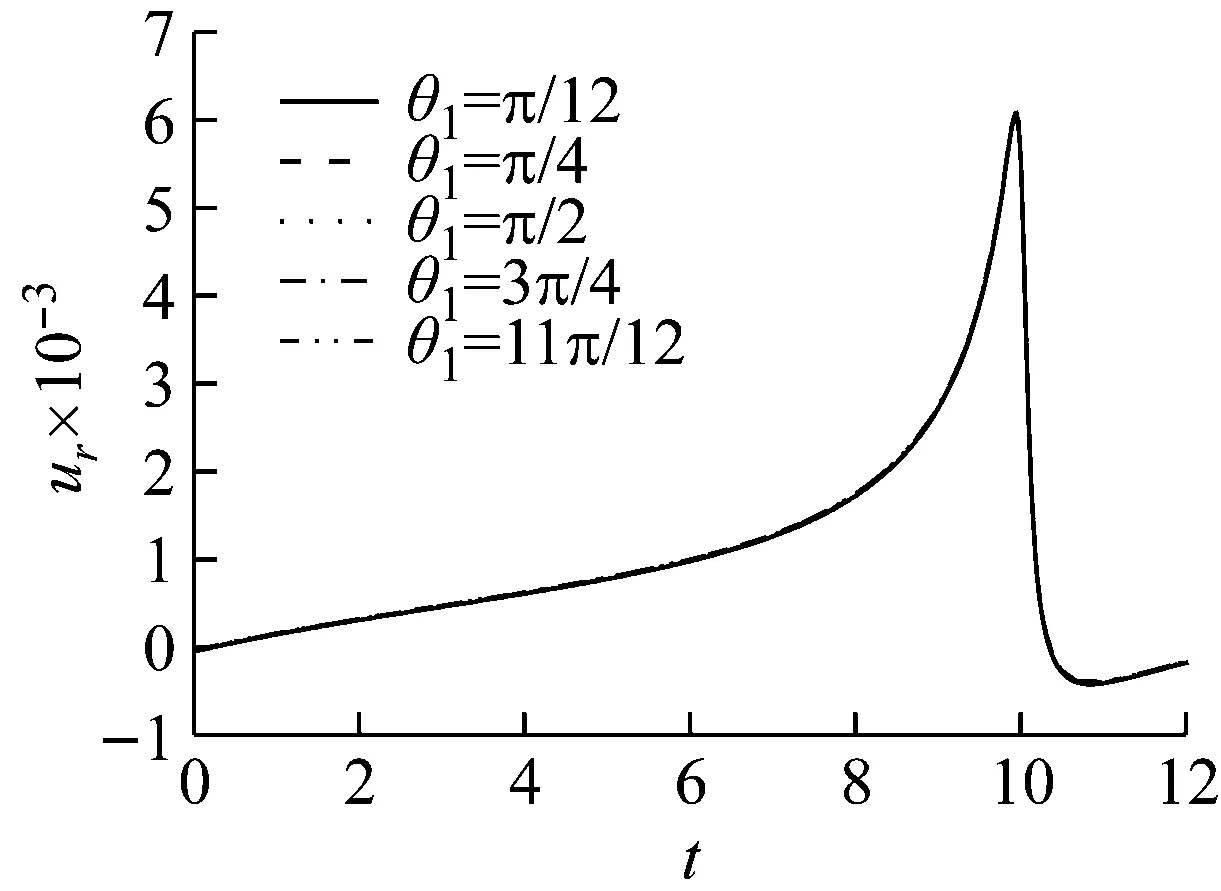
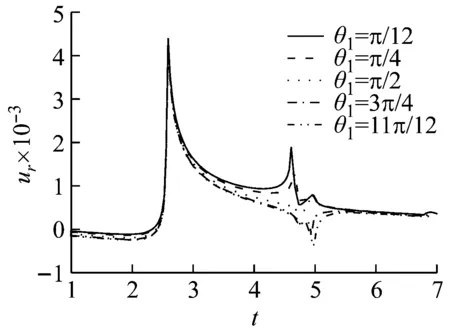
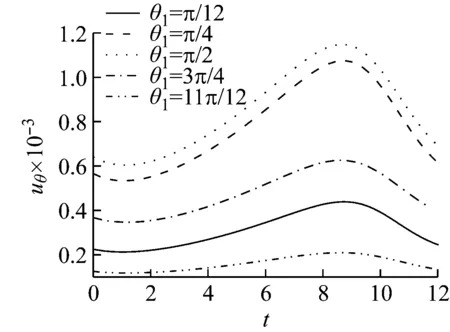
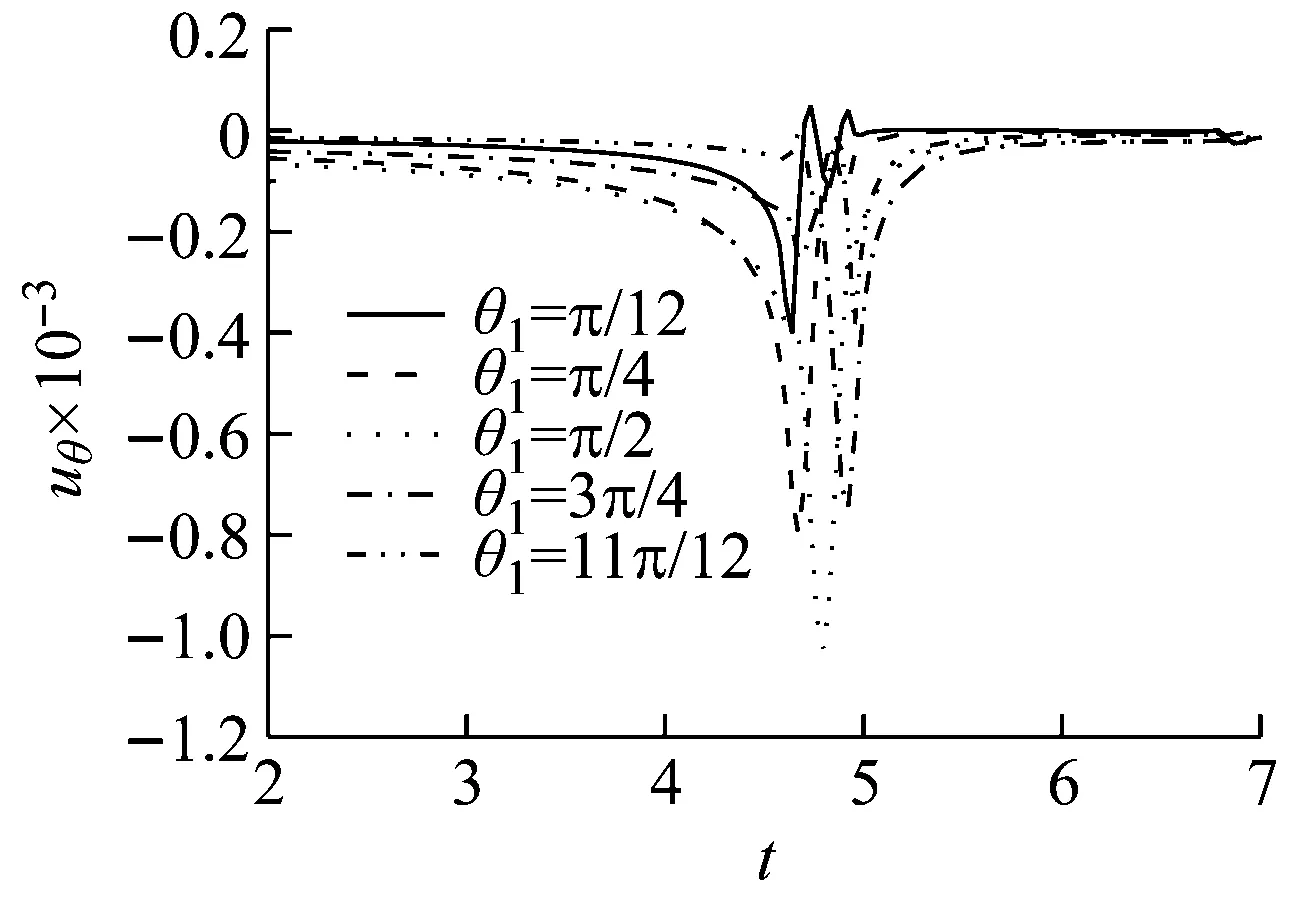
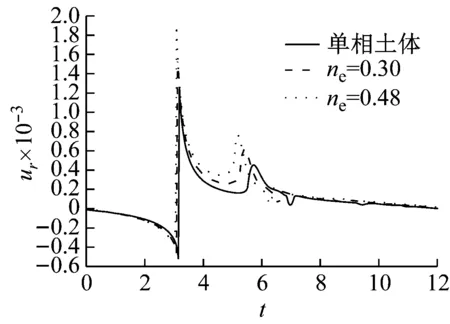
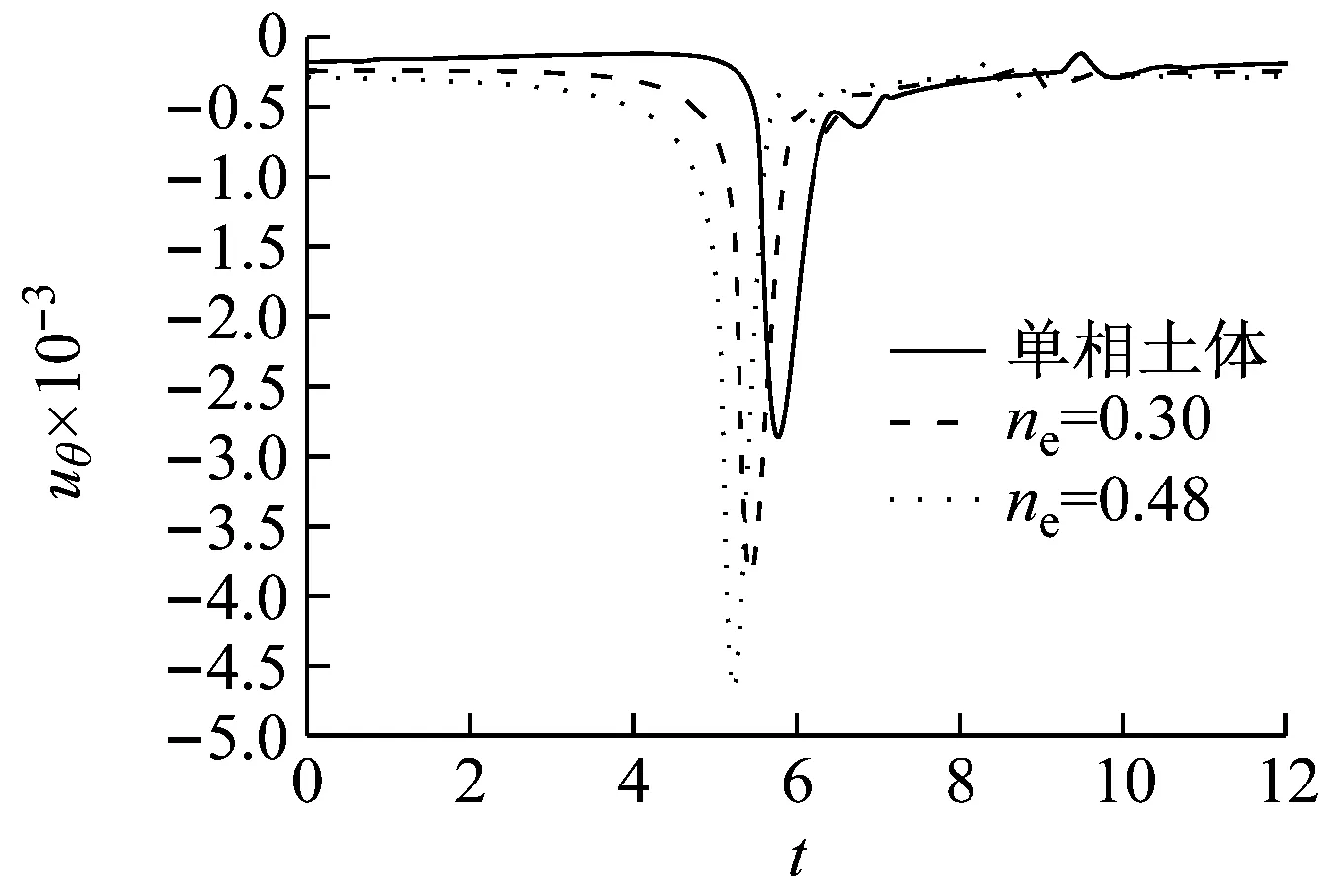
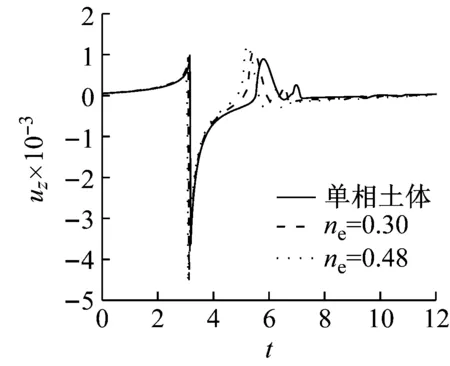
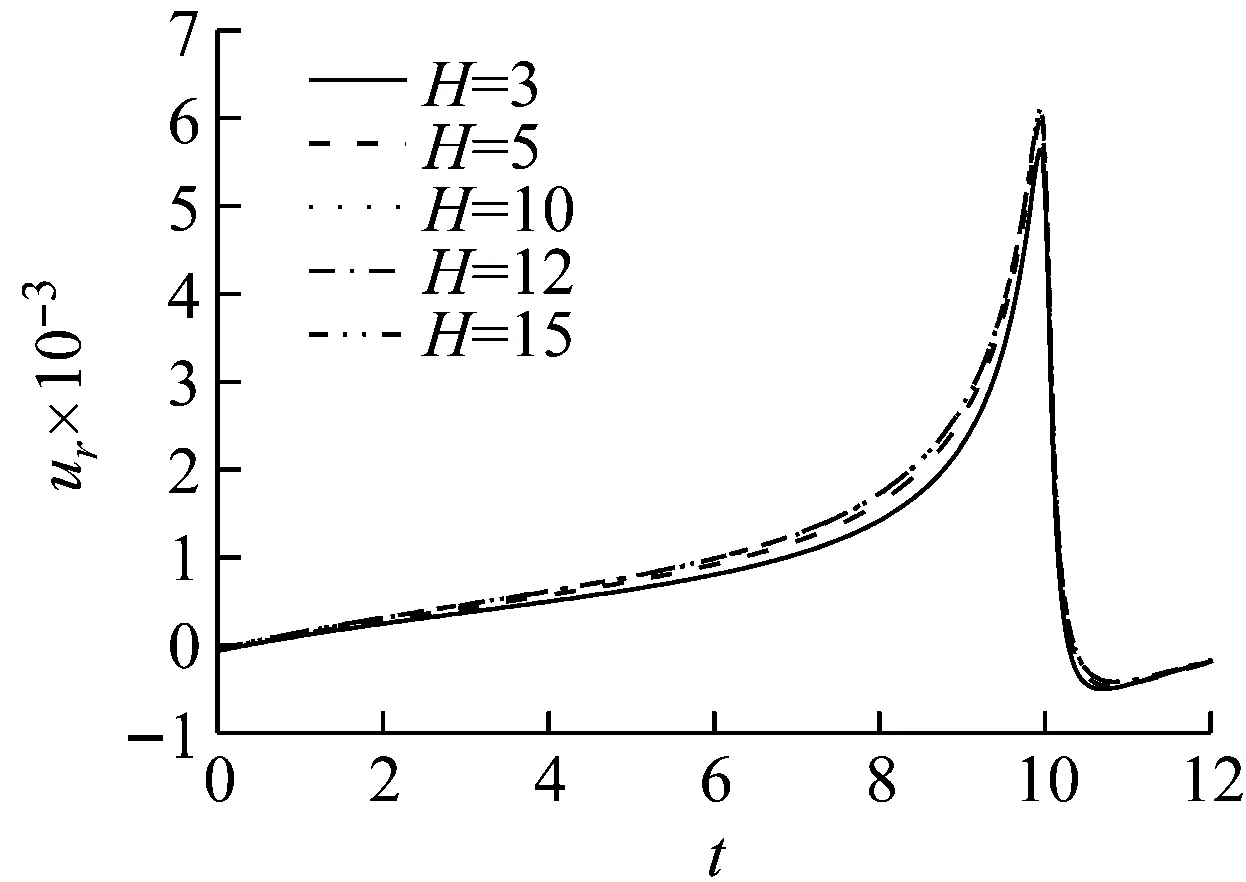
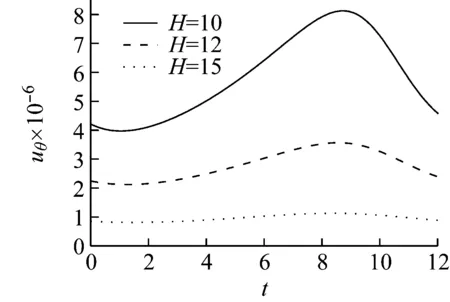
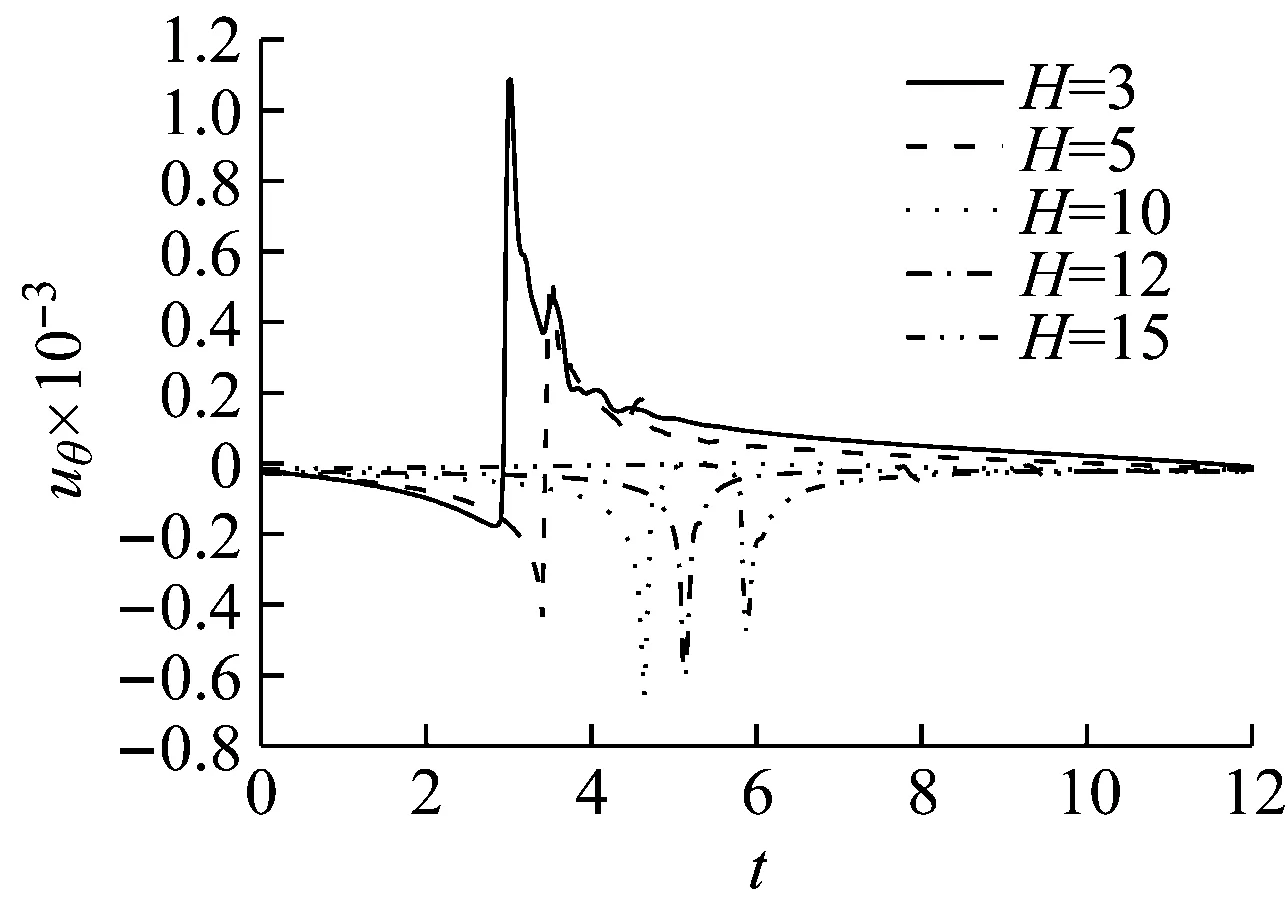
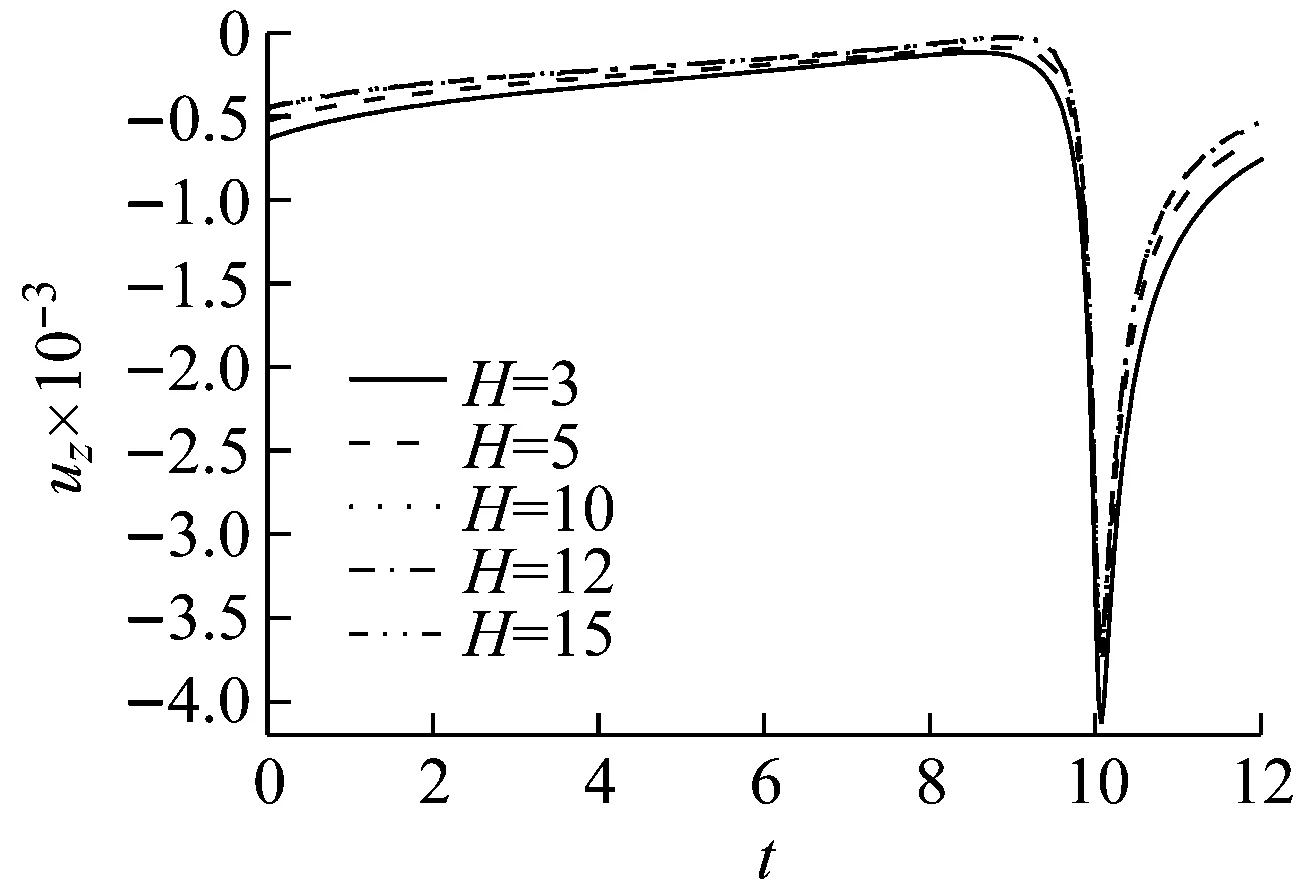
(a) v (b) v>vcr Fig.7 Influence of shear modulus on the radial vibration displacement of a particle (a) v (b) v>vcr Fig.8 Influence of shear modulus on the circumferencial vibration displacement of a particle (a) v (b) v>vcr Fig.9 Influence of shear modulus on the axial vibration displacement of a particle 无量纲隧道埋深H分别取3、5、10、12、15(由于H对不同动力响应的影响程度不同,为了清楚的反映其影响规律,以下计算中H的取值略有不同),无量纲剪切模量取1.0,其它基本参数同2.1节,图10~图12为隧道的埋深对土体径向位移、环向位移以及轴向位移的影响曲线。 (a) v (b) v>vcr Fig.10 Influence of embedded depth on the radial vibration displacement of a particle (a) v (b) v>vcr Fig.11 Influence of embedded depth on the circumferencial vibration displacement of a particle (a) v (b) v>vcr Fig.12 Influence of embedded depth on the axial vibration displacement of a particle 由图10可以看出:工况一和工况二两种情况下,ur随H的变化较小,但工况一对应的最大振幅大于工况二对应的最大幅值,这与2.2节中μ=1.0时两种工况下径向位移的响应规律相符;由图11可以看出:uθ随着H的增加而减小,工况一中达到最大振幅的时间不受H影响,工况二中达到最大振幅的时间随着H的增加而增加;由图12可以看出:uz随着H的增加有小幅度减小,工况一中,当H超过10时,uz趋于稳定;工况二中,uz随着H的增加波动性减弱,这是由于随着埋深的增大,自由表面的反射波对响应的影响越来越小。 无量纲剪切模量取1.0,无量纲隧道埋深取10,其它基本参数同2.1节,角度分别取π/12、π/4、π/2、3π/4、11π/12。图13~图15分别为不同角度处土体的径向位移、环向位移以及轴向位移曲线图。 由图13、图15可以看出:工况一中,不同角度处土体的ur和uz变化很小,而工况二中ur和uz都出现了第二波峰,这说明荷载速度大于临界速度时自由表面反射波对响应的影响更大;由图14可以看出:两种工况下,水平位置处的uθ最大,由水平位置向拱顶和仰拱处逐渐减小,拱顶处位移略大于仰拱处位移。 图16~图18分别为移动的隧道轴向常激励作用下,r1=6r0处单相土体和不同孔隙率的饱和土体的径向位移、环向位移以及轴向位移的变化曲线。无量纲剪切模量取1.0,无量纲隧道埋深取15,饱和土体的孔隙率分别取0.30和0.48。当饱和土体的参数α、M、ne、a∞、η/k等取值趋于零时,可将饱和土体退化为单相土体,轴向激励的移动速度取0.65v0和2.60v0,其中v0取ne=0.3时的速度,其它基本参数同2.1节。 由图16~图18可以看出:两种工况下,介质的孔隙率对振动响应的影响规律截然相反。工况一中,单相土体的动力响应幅值最大,随着饱和土体孔隙率的增加,动力响应幅值逐渐减小;工况二中,饱和土体的孔隙率越大,动力响应幅值越大,单相土体的动力响应幅值最小。由此可知,实际工程计算中,当v (1) 利用波函数展开法、傅里叶变换法、镜像原理等推导了移动的地铁隧道轴向激励作用下,两相多孔介质动力响应的解析解;饱和土体在隧道轴向移动激振力作用下存在临界速度,当速度达到临界速度时,饱和土体的动力响应幅值达到最大;临界速度只与饱和土体的剪切模量和密度有关,与响应频率、隧道埋深等因素无关;移动的轴向常激励作用下,饱和土体临界速度接近于土体剪切波速的1.1倍。 (a) v (b) v>vcr Fig.13 Influence of angel on the radial vibration displacement of a particle (a) v (b) v>vcr Fig.14 Influence of angel on the circumferencial vibration displacement of a particle (a) v (b) v>vcr Fig.15 Influence of angel on the axial vibration displacement of a particle (a) v (b) v>vcr Fig.16 Influence of porosity on the radial vibration displacement of a particle (a) v (b) v>vcr Fig.17 Influence of porosity on the circumferencial vibration displacement of a particle (a) v (b) v>vcr Fig.18 Influence of porosity on the axial vibration displacement of a particle (2)v (3) 移动的轴向常激励作用下,不同角度处的环向位移变化较大,不论v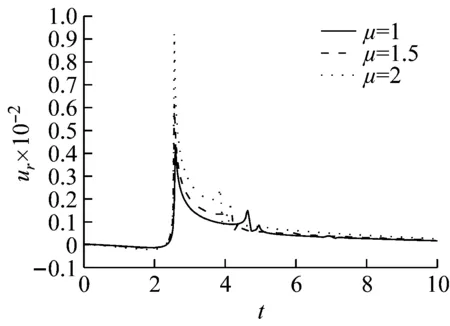



2.3 隧道埋深对动力响应的影响


2.4 不同角度的动力响应规律
2.5 孔隙率对动力响应的影响
3 结 论