变围压条件下饱和红黏土动力特性研究

吴建奇， 谢 栎， 徐 旭

(1.上海大学 土木工程系，上海 200072；2.江西理工大学 建筑与测绘工程学院，江西 赣州 341000；3.江西省环境岩土与工程灾害控制重点实验室，江西 赣州 341000)

红黏土在我国长江以南分布广泛，特别是云贵高原、两湖两广、赣南等地区更有大面积的红黏土。随着基础交通设施的快速发展，越来越多的工程建设在红黏土地基上。天然条件下，红黏土含水量一般较高，结构疏松且其收缩性很强，极易引起不均匀沉陷而导致破坏。在交通工程中，红黏土路基既承受着路堤荷载的静荷载作用，又承受着交通荷载的动荷载作用。交通荷载是种特殊的振动荷载，能让土体经历几十万次甚至上百万次的循环作用，可能产生的问题往往就是沉降过大。所以充分了解红黏土在交通荷载下的动力特性，能更好的指导和服务实际交通工程[1-4]。许多学者利用常规动三轴仪研究黏土在交通荷载下的动力特性，取得了颇丰的成果，如陈颖平等[5]、张勇等[6]、张茹等[7]对软黏土循环荷载下的动力特性进行了系统研究。胡秀青等[8]利用多向动单剪系统研究了水平双向耦合荷载作用下循环剪应力比和相位差对饱和软黏土动力特性的影响。然而常规的动三轴、动单剪试验，只能施加一个动应力分量，并不存在动应力分量的耦合，应力路径较为简单。但是，当存在两个甚至多个动应力分量时，应力路径就会变得复杂。众多试验结果表明，不同动应力分量的耦合对饱和土体的动力特性产生很大的影响。Kammerer等[9]通过双向动单剪试验发现动剪应力的耦合对瞬时孔压产生较大影响。虞海珍[10]通过动扭剪试验研究了循环偏应力和循环扭矩耦合对动孔压的影响。

交通荷载下路基土单元体除了承受竖向循环荷载之外，水平向也存在与竖向荷载相对应的循环动应力，也就是循环围压。上述的常规三轴仪、空心扭剪仪和双向动单剪仪等仅考虑了轴向循环荷载，或者轴向循环剪切，而忽略了循环围压对黏土单元体长期变形的影响。而施明雄等[11-12]表明，循环围压，即变围压对土体的孔压、模量、变形都存在较大的影响。因此，有必要在三轴试验中考虑循环围压应力路径的影响。

随着试验仪器的革新，能够考虑循环围压的三轴仪已在国内一些实验室中得到了运用。谷川等[13]通过循环偏应力与循环围压的耦合模拟真实交通荷载下竖向循环正应力与水平循环正应力的耦合，研究了循环围压对饱和软黏土孔压、永久和回弹变形的影响。蔡袁强等[14]通过不排水循环三轴试验分别在单、双向激振下对杭州软黏土的动力特性进行研究；王军等[15]采用双向动三轴设备进行一系列饱和软黏土的变围压动三轴试验，研究循环偏应力和循环围压耦合对饱和软黏土孔压特性的影响。上述研究结果揭示了变围压应力路径试验对饱和软黏土动力特性具有较大影响。但其试验土体主要为江浙地区的软黏土，尚未见对红黏土的系统性研究。

因此，本文采用GDS变围压动三轴系统，对赣南地区原状红黏土分别开展了变围压(VCP)应力路径试验和常围压(CCP)应力路径试验，对比分析了两种应力路径试验在相同的最大应力状态，相同的平均应力状态，相同的最小应力状态下的孔压发展、回弹模量和累积变形情况，提出了通过基于常围压试验结果预测变围压试验结果的经验公式。

1 试验土样及方案

1.1 试验仪器

本文试验采用英国GDS公司研发的动三轴测试系统，如图1所示。仪器主要由轴向激振器，围压控制器，轴向力与位移传感器，孔压及围压传感器，反压器，信号调节装置及动态控制系统组成。仪器通过压力室底座施加轴向力和轴向变形，控制压力室液体进出施加围压，测得反压器液体体积的变化量计算排水试验中试验的体应变。仪器精度较高，其中轴向位移精度7%，轴力精度0.2 N，围压和孔压传感器精度1 kPa,反压体积精度1 mm3,能精准控制施加的压力，确保试验结果准确可靠。

图1 GDS三轴仪器示意图

1.2 试验土样

本试验采用原状红黏土试样，取自天然路基层，取样深度为2～2.5 m。采用薄壁取样法，尽量减少对原状土的扰动。取完样后，立即对薄壁管两端进行密封，储存在实验室的恒温恒湿箱内以备试验使用。通过标准土力学试验测得试验所用原状红黏土基本物理性质进行调查，结果如表1所示。

表1 赣南红黏土的基本物理性质

1.3 固结过程

首先采用专用切样器，将原状土样切成尺寸为直径50 mm，高100 mm的试验试样，然后将试样装入GDS三轴压力室进行反压饱和。分三阶段逐级施加300 kPa反压，310 kPa围压,保持10 kPa有效压力，饱和24 h后采用B检测检验土样的饱和程度，试验的孔压系数B值大于0.98则认为土样达到饱和要求。最后施加设定的围压进行等压固结，当孔隙水压力消散到等于反压时，认为土样固结完成。

1.4 应力路径

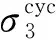
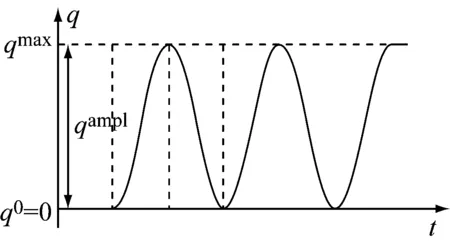
(1)

(2)

(3)

q0=0

(4)

(5)

(6)

在常规三轴中，由于围压恒定，即：

(7)

则应力路径的斜率ηampl可计算得到

(8)

对于变围压三轴试验，则有：

(9)

由式(7)可知，在变围压试验中，应力路径的斜率ηampl<3，即小于常围压下的应力路径斜率。

本文定义循环应力比CSR来表明应力路径的高度(即循环偏应力的幅值)

(10)

本文定义回弹模量为

(11)

1.5 加载方案

本文三轴试验采用应变控制模式，加载频率为1 Hz，加载波形为半正弦波，循环次数为100 000次，在排水条件下进行，将试样顶部与反压器相连形成排水通道，孔压在底部测得。整个加载过程中偏应力q和围压σ3一直以同相位做循环振动，加载波形如图2所示。

(a)

(b)

试验分为A、B、C共3组， A组代表部分排水条件下常围压试验和变围压试验具有相同的最大应力状态，即σmax相等，B组代表部分排水条件下其具有相同的平均应力状态，即σav相等，C组代表部分排水条件下其具有相同的最小应力状态，即σmin相等，三组应力路径如图3所示。具体试验方案如表2所示，其中A1、B1、C1，A4、B4、C4分别为同一组常围压试样，作为三组部分排水条件下不同应力路径变围压试验的共同对照组试验。

(a) 相同最大应力状态

(b) 相同平均应力状态

(c) 相同最小应力状态

图3 CCP与VCP应力状态

Fig.3 Stress state of CCP and VCP tests

2 试验结果及分析

2.1 孔 压

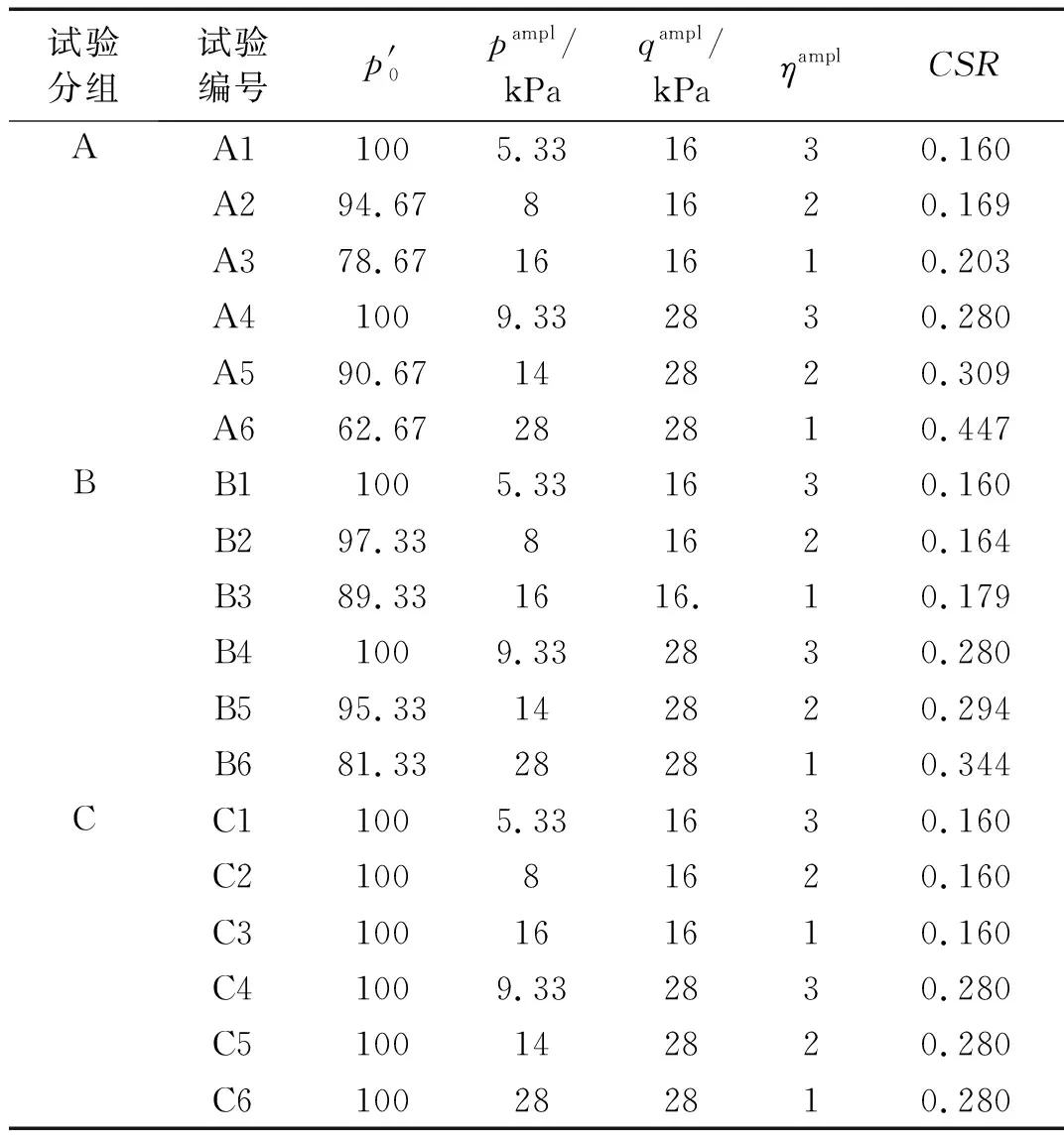
表2 加载方案

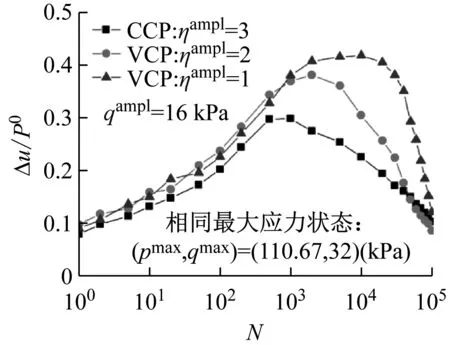
(a) qampl=16 kPa

(b) qampl=28 kPa

图4 相同最大应力状态孔压比随循环次数的发展曲线

Fig.4 Normalized pore water pressure ratio accumulations versus number of cycles in identical maximum stress state

(a) qampl=16 kPa

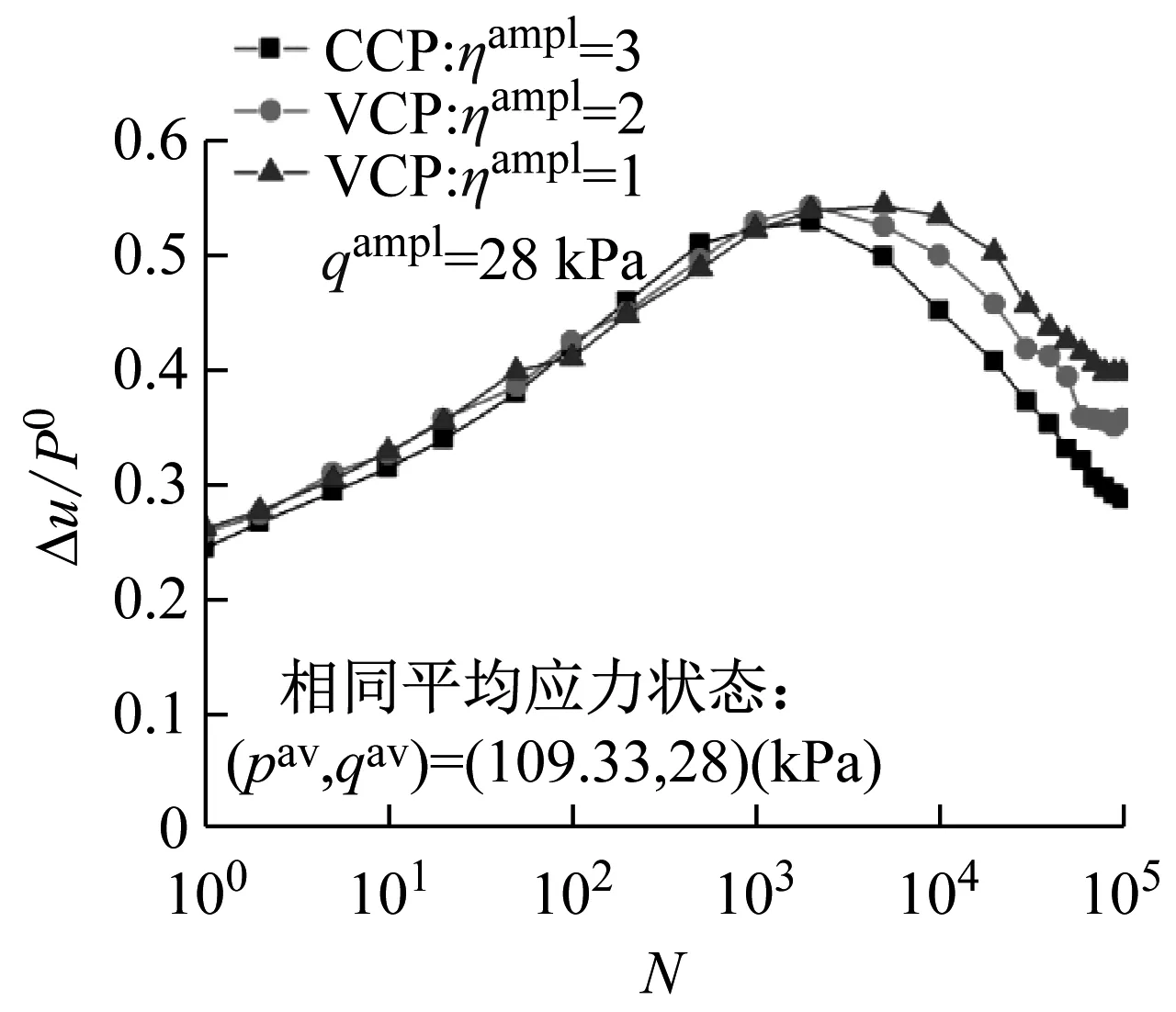
(b) qampl=28 kPa

图5 相同平均应力状态孔压比随循环次数的发展曲线

Fig.5 Normalized pore water pressure ratio accumulations versus number of cycles in identical average stress state

(a) qampl=16 kPa

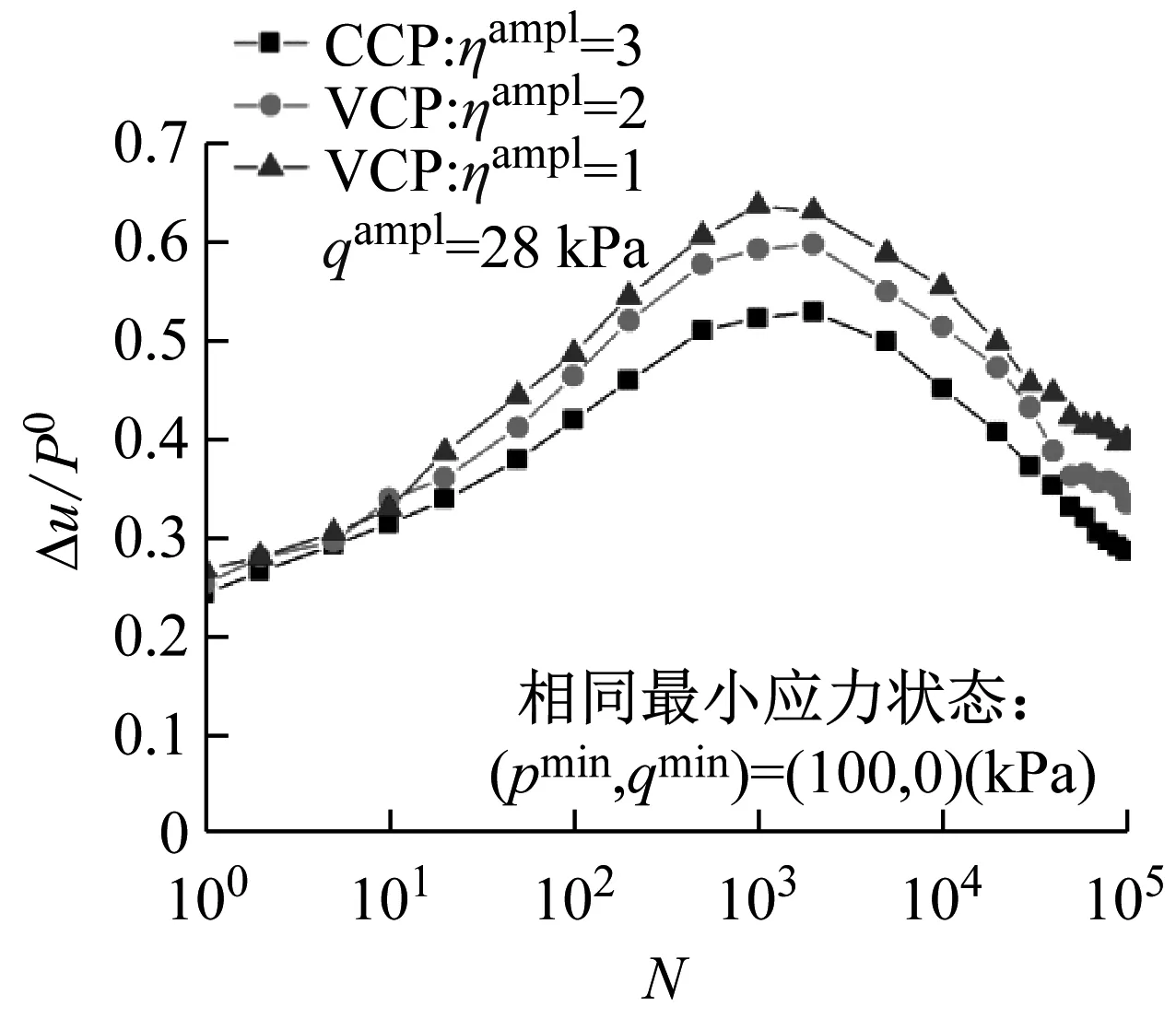
(b) qampl=28 kPa

图6 相同最小应力状态孔压比随循环次数的发展曲线

Fig.6 Normalized pore water pressure ratio accumulations versus number of cycles in identical minimum stress state

2.2 模 量

图7～图9所示为三种应力状态不同应力路径试验中回弹模量Mr随循环次数的发展曲线。由图中曲线可知，无论循环应力比CSR如何变化，回弹模量Mr随循环次数的变化规律基本相同，即循环加载初期，回弹模量首先快速降低，随着循环次数的增加，回弹模量Mr影响减小的速率逐渐降低，最后趋于增加或保持稳定的过程，这是由于试验初期，孔压迅速积累，有效应力降低，回弹模量相应出现的较大的衰减，随着循环次数的增加，孔压逐渐消散，有效应力增加，回弹模量出现一定程度的增加，或保持稳定。对比图7、8中(a)与(b)可以看出，在相同试验条件下，循环应力比CSR越大，土体的回弹模量Mr减小；在相同的循环偏应力幅值qampl条件下，在循环加载试验初期，相对于常围压CCP试验，变围压VCP试验的回弹模量Mr的衰减速率更大，但随着循环次数的增加，不同应力路径回弹模量发展曲线非常类似，表明在相同平均应力状态下，不同应力路径斜率对回弹模量的影响可以忽略。

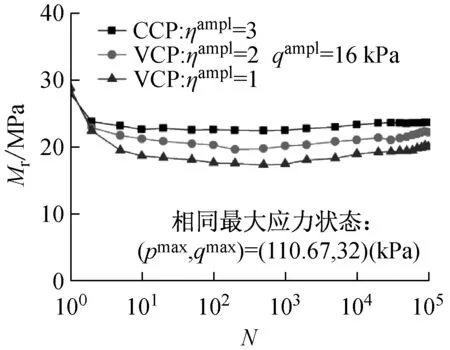
(a) qampl=16 kPa

(b) qampl=28 kPa

图7 相同最大应力状态回弹模量随循环次数的发展曲线

Fig.7 Rebound modulus versus number of cycles in identical maximum stress state

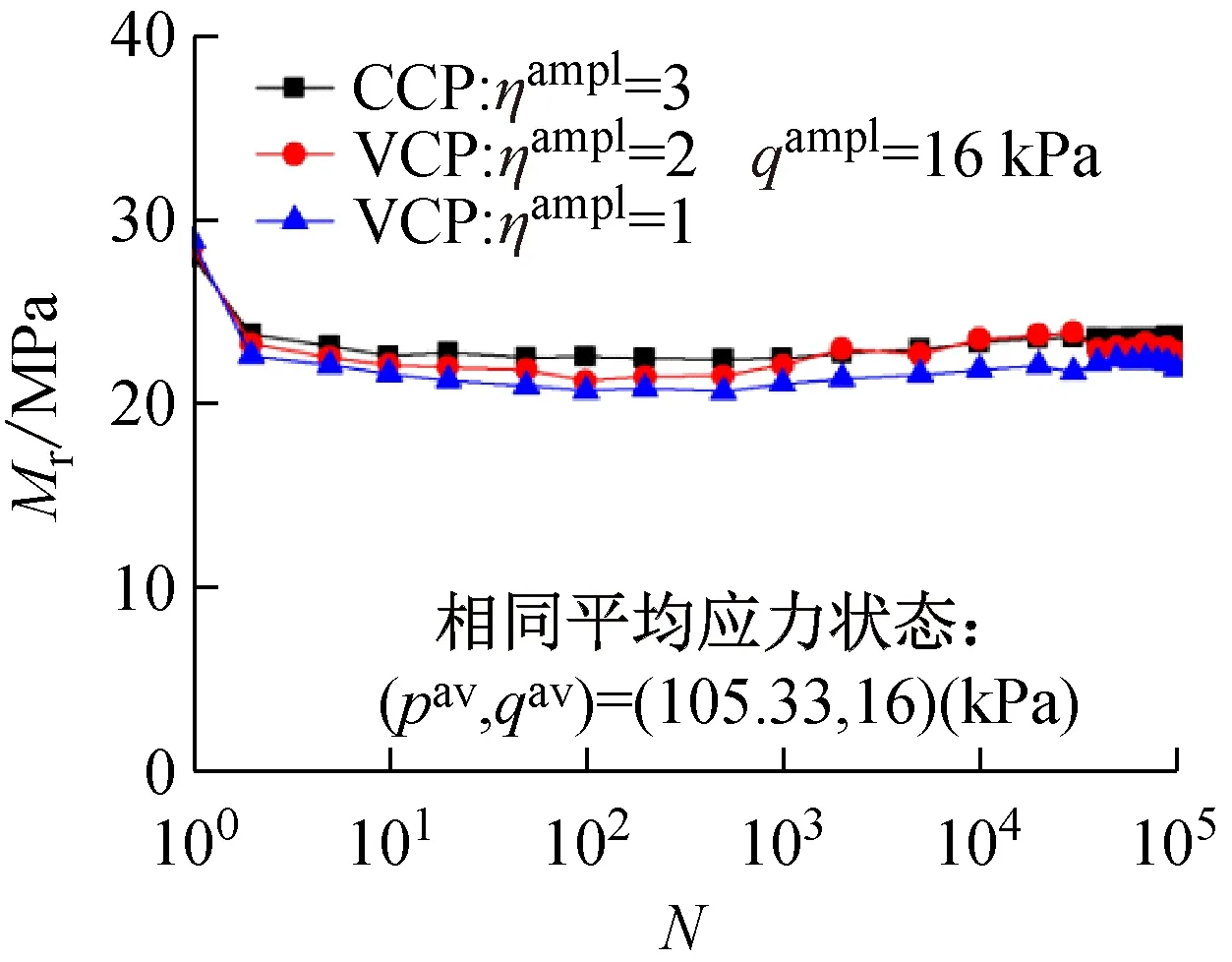
(a) qampl=16 kPa

(b) qampl=28 kPa

图8 相同平均应力状态回弹模量随循环次数的发展曲线

Fig.8 Rebound modulus versus number of cycles in identical average stress state

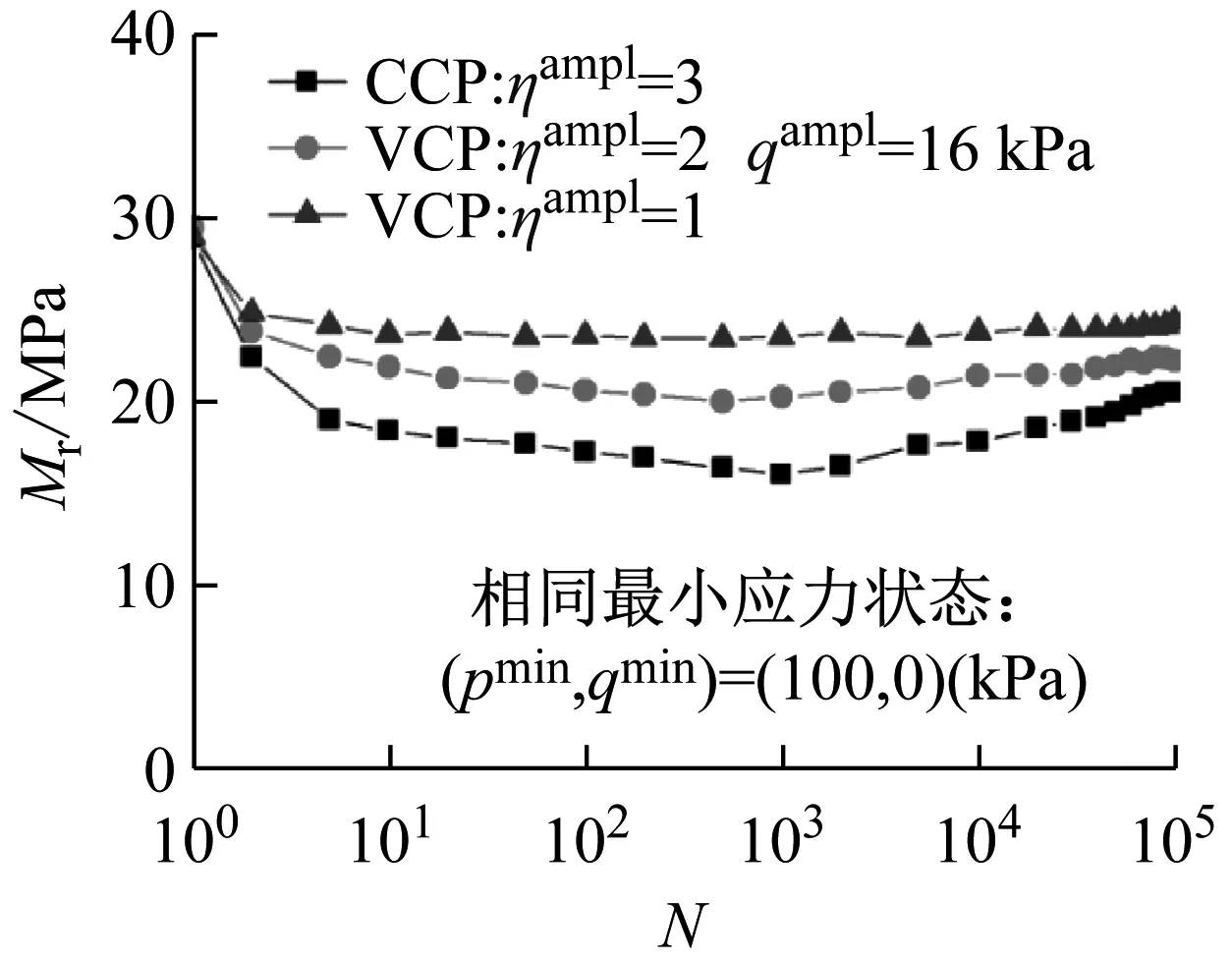
(a) qampl=16 kPa

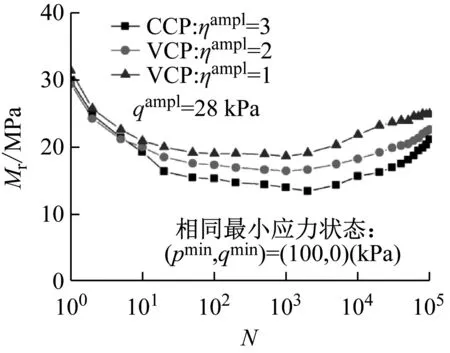
(b) qampl=28 kPa

图9 相同最小应力状态下回弹模量随循环次数的发展曲线

Fig.9 Rebound modulus versus number of cycles in identical minimum stress state

从图9与图7、8进行对比分析，在相同最小应力状态下，在不同实验条件及不同应力路径下，其回弹模量的发展曲线基本都相似，但对于不同的循环偏应力幅值qampl，回弹模量都随应力路径斜率ηampl的减少而增大。综合可以得出，在相同的最大应力状态下，变围压应力路径下试样弹模量小于常围压下的回弹模量，且随应力路径斜率减小而减小。而对于相同的最小应力状态，试样的回弹模量呈现出相反的趋势。而对于相同的平均应力状态试验，则两种围压条件下的回弹模量十分接近。

2.3 累积变形

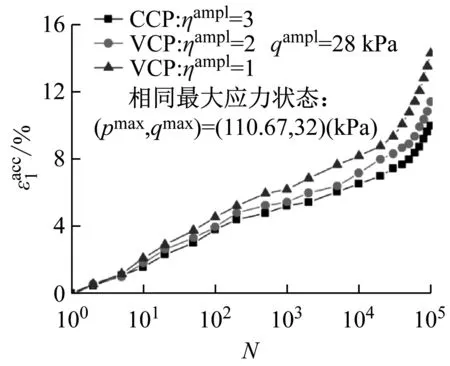
从图10～图12中曲线可以看出，无论应力状态及循环应力比CSR如何变化，竖向累积变形随着循环次数的增大而增大，此外，所有曲线的变化规律基本相似，循环加载初期，竖向累积变形增大较大，当循环加载500次以后，竖向累积变形速率逐渐趋缓，但是当循环加载10 000次后，竖向累积变形急剧增加，表明土体发生破坏。在相同的最大应力状态下，变围压应力路径试验的竖向累积变形大于常围压应力路径下的竖向累积变形，且随着应力路径斜率ηampl的减少而不断增大；在相同的平均应力状态下，变围压应力路径试验的竖向累积变形与常围压下的发展规律类似，与应力路径斜率无关；在相同的最小应力状态下，变围压应力路径试验的竖向累积变形大于常围压应力路径下的竖向累积变形，且随着应力路径斜率ηampl的减少而不断减少。 基于此，在保证循环偏应力幅值qampl相同的基础上，提出了通过常围压试验结果预测变围压试验下累积变形值的经验公式

(12)

pav=(qmax+q0)/2

(13)

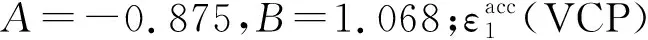
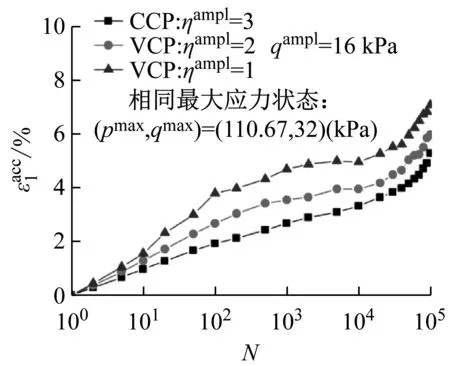
(a) qampl=16 kPa

(b) qampl=28 kPa

图10 相同最大应力状态下竖向累积变形随循环次数的发展曲线

Fig.10 Axial strain accumulations versus number of cycles in identical maximum stress state

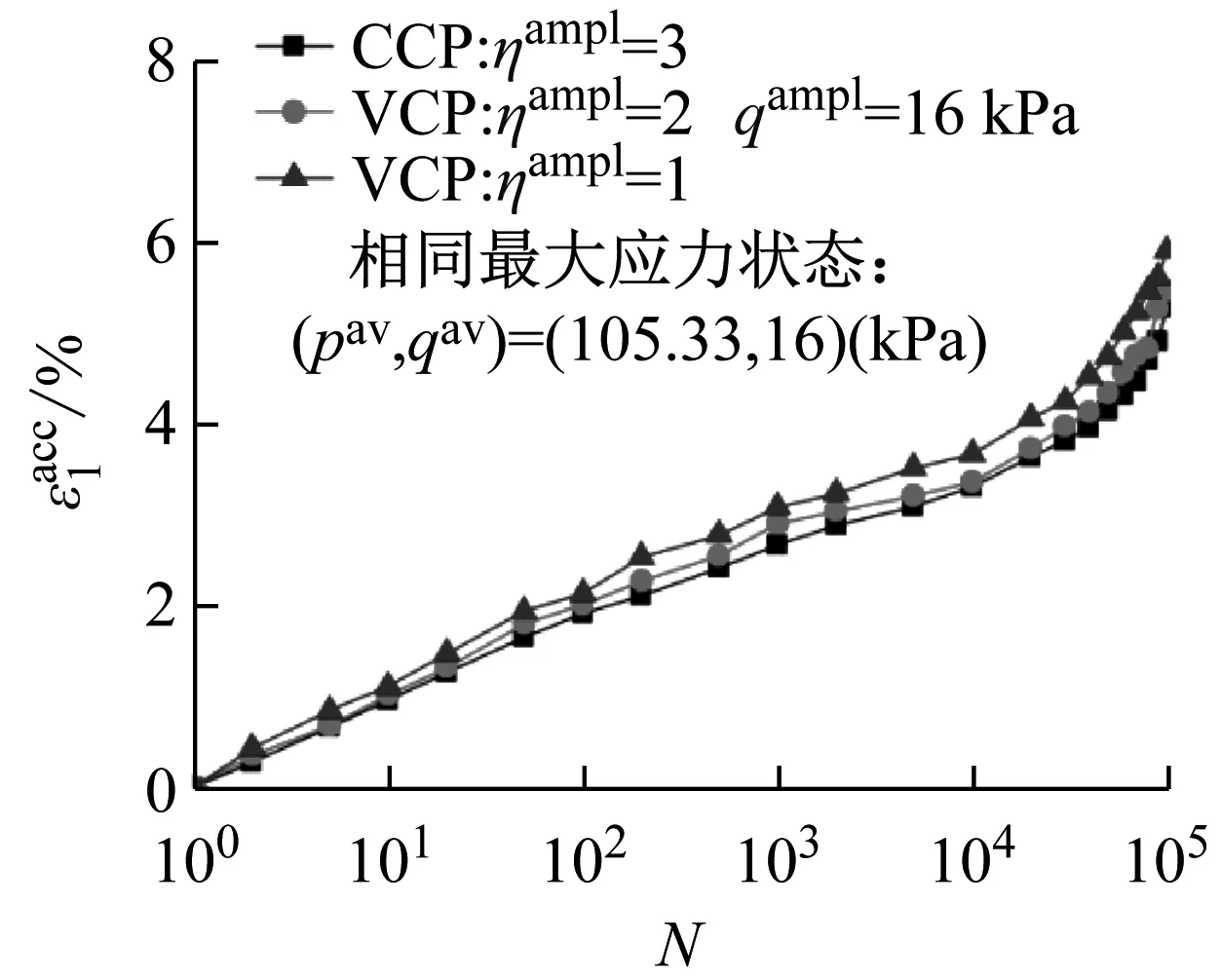
(a) qampl=16 kPa

(b) qampl=28 kPa

图11 相同平均应力状态下竖向累积变形随循环次数的发展曲线

Fig.11 Axial strain accumulations versus number of cycles in identical average stress state

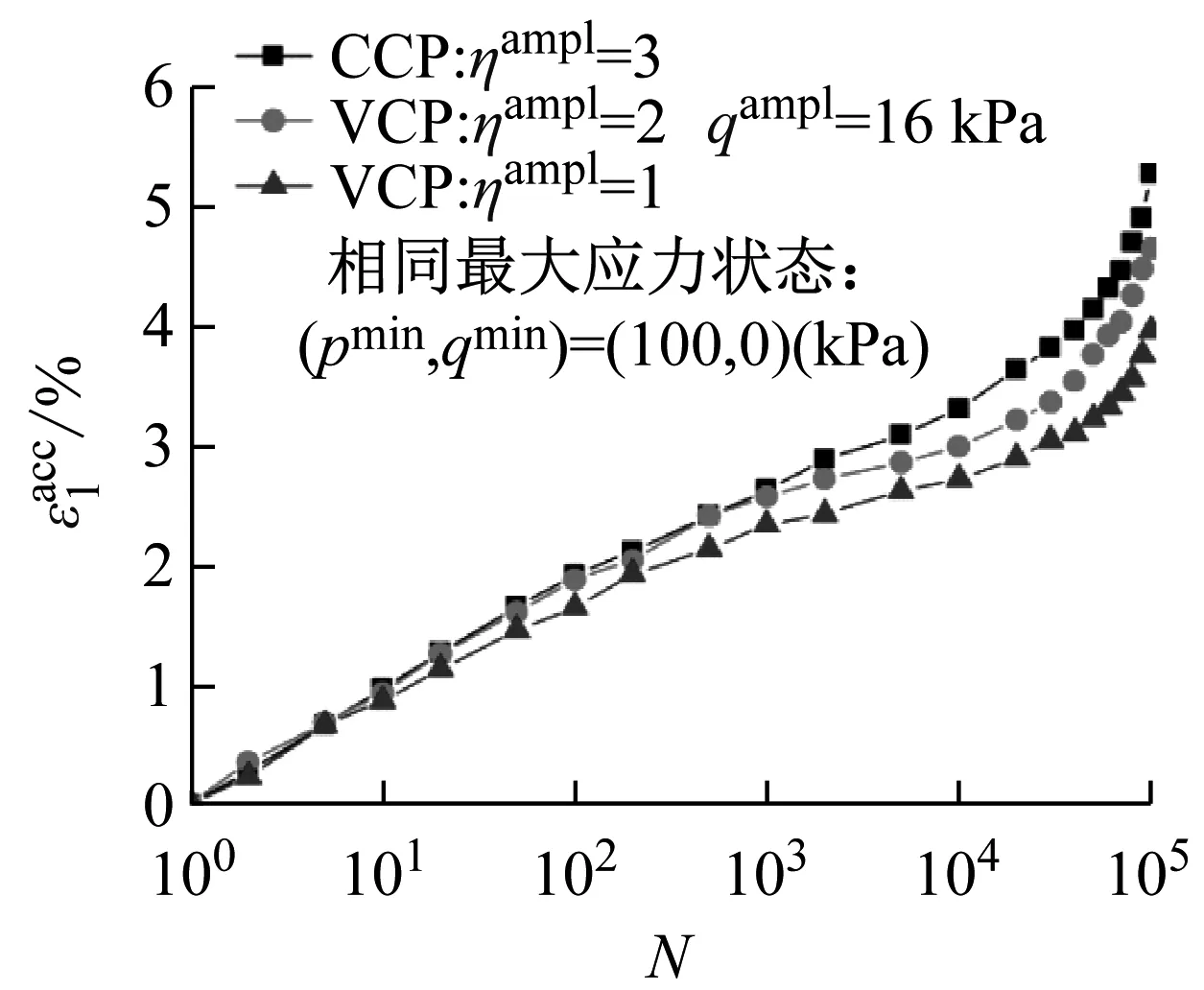
(a) qampl=16 kPa

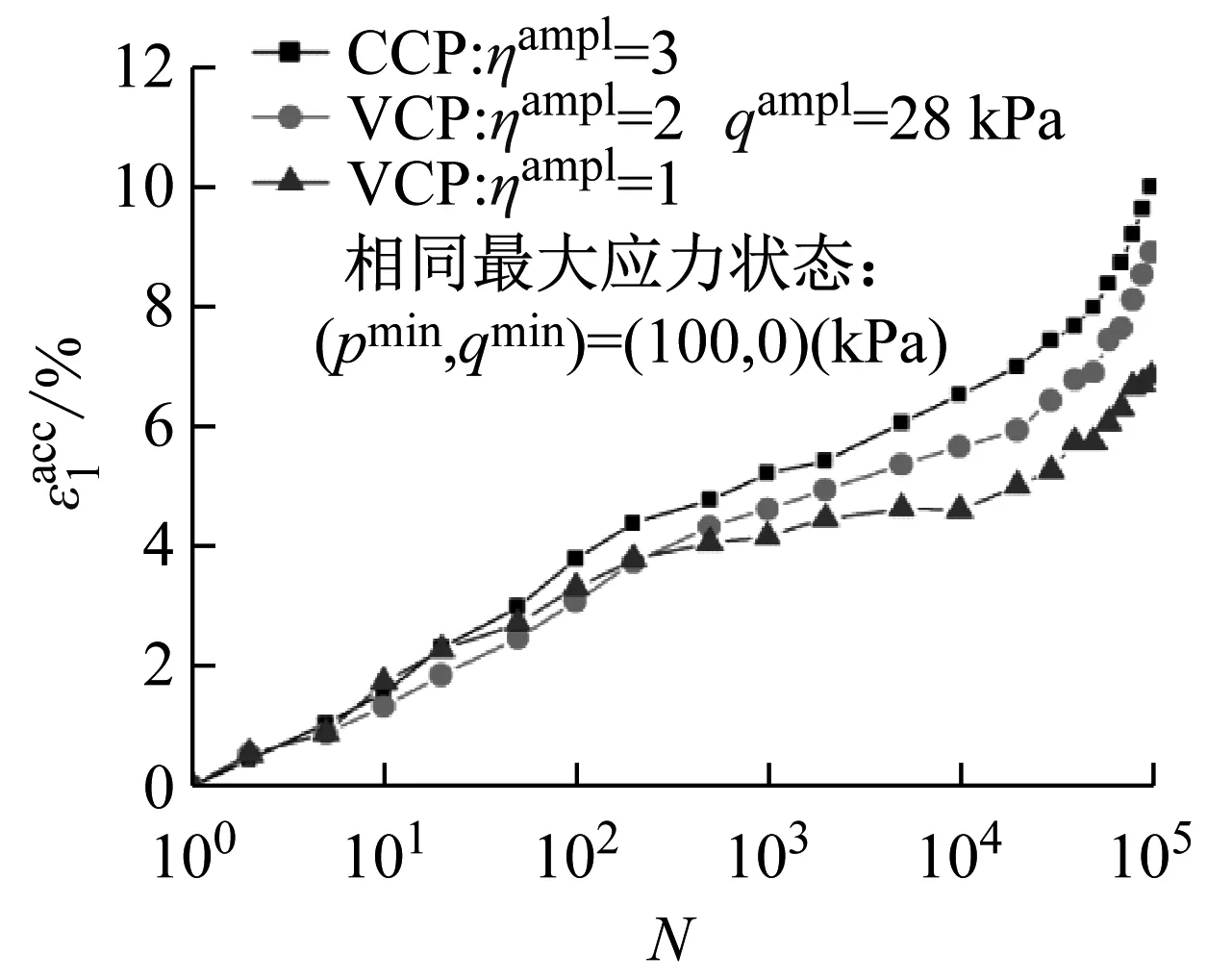
(b) qampl=28 kPa

图12 相同最小应力状态下竖向累积变形随循环次数的发展曲线

Fig.12 Axial strain accumulations versus number of cycles in identical minimum stress state

图13(a)和(b)分别为循环偏应力幅值qampl为16 kPa和28 kPa下各应力状态试样归一化的竖向累积变形与循环次数的发展规律。图13(a)和(b)中曲线较好的重合性，表明上式通过常围压试验预测变围压试验的适用性。

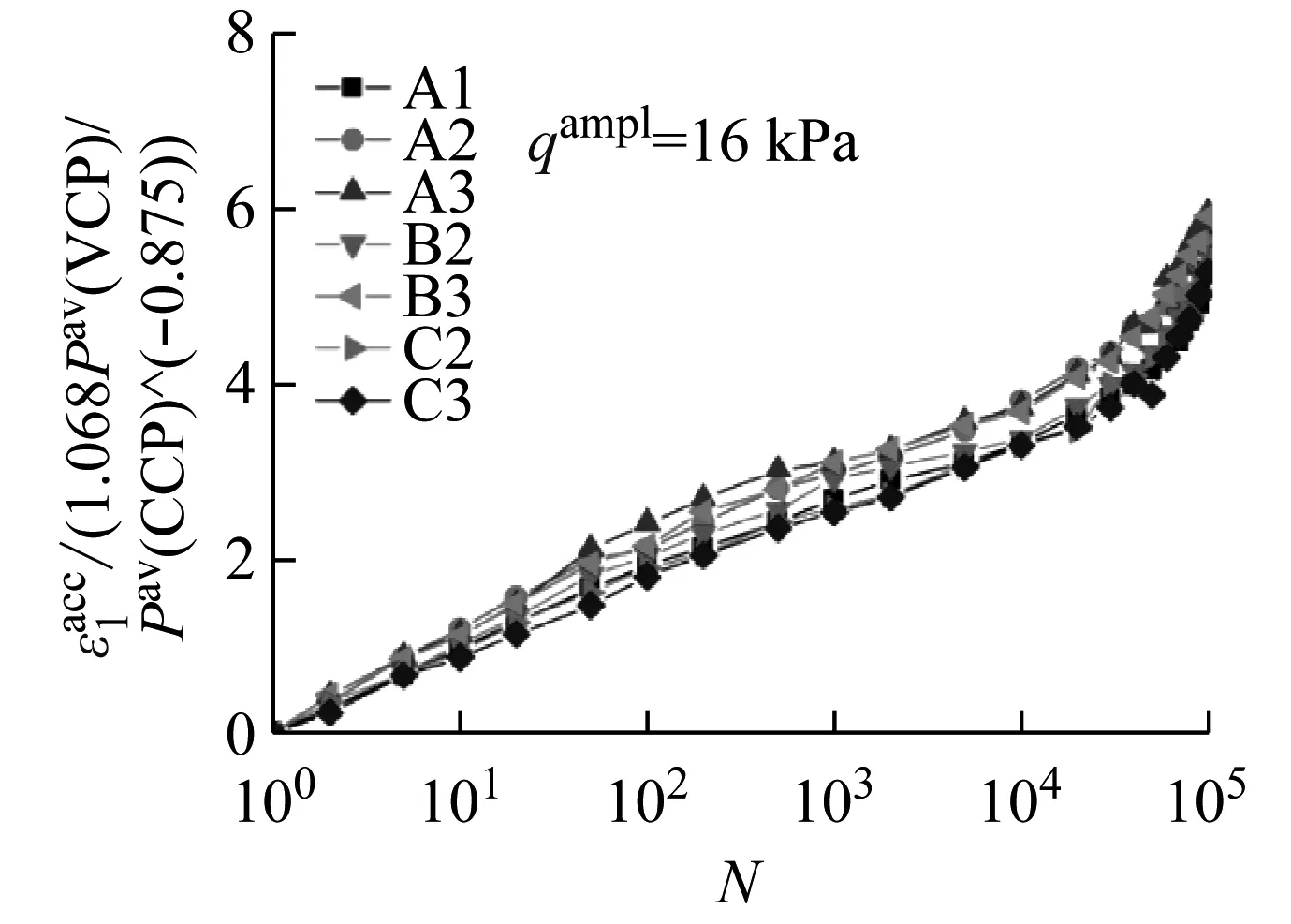
(a)qampl=16 kPa

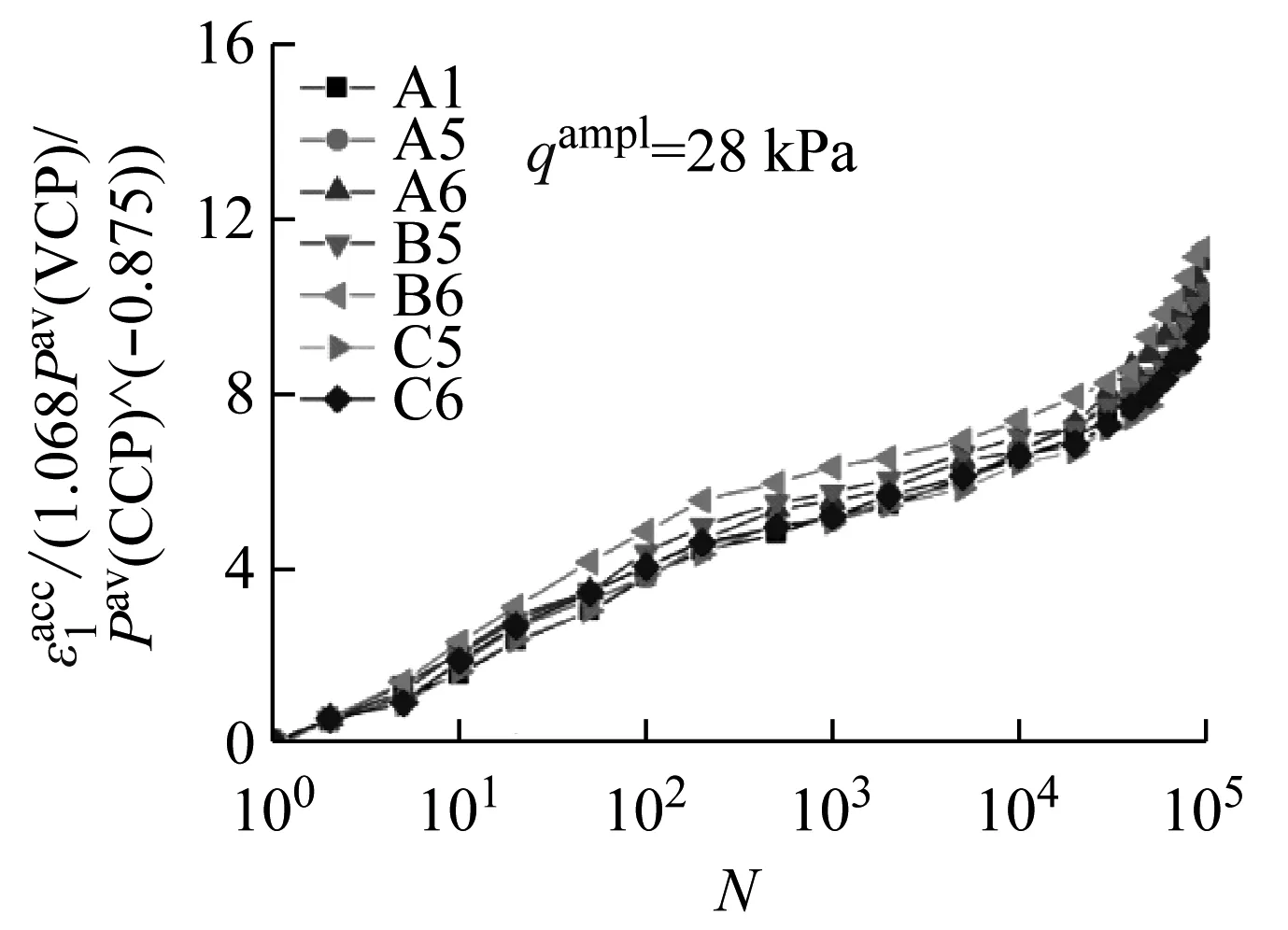
(b)qampl=28 kPa

图13 归一化的竖向累积变形随循环次数的发展曲线

Fig.13 Normalized axial strain accumulations versus number of cycles for test series

2.4 饱和红黏土累积变形预测模型的验证

为了能够通过常围压试验条件下饱和红黏土的循环累积变形情况来预测变围压试验条件下的循环累积变形情况，对文中的式(12)的准确性进行判定。利用式(12)对文献[13]中的试验方案4～6中CSR=0.208条件下试验得到的永久应变与加载周期关系曲线进行验证，其结果如图14所示。

从图14中可以看出，经验公式拟合曲线与文献[13]所得的曲线都趋于一致。随着循环加载增大，当N=10 000情况下，ηampl=1.0时Δεp=0.098 5，在ηampl=1.5时Δεp=0.116 7。可见：在相同CSR情况下，模型所得拟合曲线与试验曲线都趋于一致，随着循环次数的增加，其Δεp值越来越大，主要原因是由于式(12)是根据饱和红黏土进行试验而得出的，而验证对象是饱和黏性土，这两者之间在工程性质等方面存在一定的差异性，导致了试验结果的偏差，但是总体趋势是一致的，说明本文建立的式(12)是合理的。

图14 相同最小应力状态下竖向累积变形随循环次数的发展曲线

Fig.14 Axial strain accumulations versus number of cycles in identical minimum stress state

3 结 论

本文利用GDS动三轴测试系统研究了赣南地区天然红黏土动力特性，对比分析了相同最大应力、相同平均应力、相同最小应力三个应力状态下，变围压因素对红黏土的影响，得到主要结论如下：

(1) 孔压随着循环次数整体呈现先增加到峰值后减少的趋势，回弹模量随循环次数呈现出先降低后逐渐增加或保持稳定的过程。

(2) 对比三种应力状态(相同最大应力、相同平均应力、相同最小应力)，变围压应力路径较相应的常围压而言会导致孔压一定程度的增加。

(3) 对于相同的最大应力状态，变围压应力路径会导致试样红黏土模量降低，变形增加，应力路径斜率越大，变化越明显，而对于相同的最小应力状态，则呈现出相反的趋势。对于相同平均应力的常围压试验和变围压试验，变围压应力路径对红黏土的回弹模量和累积变形影响不明显。

(4) 提出了考虑平均应力状态的通过常围压试验结果预测变围压试验结果的经验公式，能准确预测不同应力路径的红黏土竖向累积变形。