低承台管桩纵向自由振动特性分析
官文杰, 吴文兵,2, 蒋国盛, 梁荣柱, 徐宝军
(1.中国地质大学 工程学院 岩土钻掘与防护教育部工程研究中心,武汉 430074;2.广西大学 土木建筑工程学院广西防灾减灾与工程安全重点实验室,南宁 530004;3.山东省城乡建设勘察设计研究院,济南 250031)
随着我国基础设施建设的高速发展,对桩基础的需求也日益增大,其中低承台桩基础作为一种基础形式而广泛应用于工业与民用建筑工程。与无承台桩基础相比,低承台桩基础还受到承台底土和承台侧土的约束,使得低承台桩基础与土的静动力相互作用更加复杂。近年来,国内外学者对低承台桩基的静动力特性进行了大量研究。在低承台桩基的静力特性方面,丁翠红等[1]、杜家庆等[2]采用数值模拟方法,分别研究了承台的存在对单桩水平承载力的影响和竖向荷载下群桩-土-承台的相互作用机理;王浩等[3]基于室内模型试验,对比研究了带承台单桩和双桩的桩间土变形及桩周土应力分布规律;Arshakuni等[4]根据现场试验,讨论了低承台的存在对软土中单桩抗压性能的影响;于绅坤[5]运用透明土技术与粒子图像测速技术相结合的试验方法,研究了带承台单桩在竖向荷载作用下桩周土体的变形规律。
低承台桩基础的动力特性也是学者们关注的研究热点之一。在低承台桩基的抗震与减震设计方面,唐亮等[6]采用振动台试验,研究了可液化场地中承台型式对桥梁桩-柱墩地震反应的影响,试验表明可液化场地中低承台桩的抗震性能优于高承台桩;王平[7]采用有限元法,分析了在竖向静载和水平动载同时作用下,不同地震波对群桩-土-承台动力相互作用的地震反应的影响规律;王辉[8]采用三维弹塑性有限元法,研究了水平地震荷载下,桩-土-结构的动力相互作用。在低承台桩基的完整性检测方面,李浩[9]基于弹性波动理论,采用有限差分法分析了承台横截面积、承台厚度、激振力时间、激振力位置等因素对低应变曲线的影响规律;周乃明[10]采用数值模拟法,结合现场试验数据,对机械阻抗法在既有承台单桩的完整性和承载力判定上的应用进行了研究;王奎华等[11-12]求解出了低承台实心桩基础中承台纵向自由振动位移频域解析解及时域半解析解,在承台桩基础振动特性的理论研究方面取得了重大突破。
以上研究主要是关于低承台实心桩基础的静动特性的研究,对低承台管桩动力特性的研究则很少见。然而低承台预应力混凝土管桩作为一种基础形式,已广泛应用于建筑、铁路、公路、港口、市政等各个领域,承台将上部结构荷载传递给承台周围土体及管桩,管桩再将其传递到桩侧土、土塞及深层较硬的岩土层上,承担竖向和水平承载能力,减小低承台桩土系统的变形,保证建构筑物的稳定安全。前人在不考虑承台的情况下,针对管桩的动力特性展开了大量的研究[13-14],但少有人考虑土塞质量的影响,Wu等[15]提出了附加质量模型来模拟土塞与管桩之间的动力相互作用,并基于此模型系统的研究了管桩的纵向及扭转振动特性,研究表明土塞质量对管桩振动特性的影响不可忽视[16-17]。现有文献中关于低承台管桩动力特性的研究相对较少,仅李曰辰等[18]通过振动台模型试验,在考虑土-桩-结构相互作用的条件下研究了PHC管桩的抗震性能;黄晓龙等[19]采用有限元法,研究了无承台单桩及带承台单桩的水平受力特性,结果表明承台的存在显著减小了桩身位移,提高了桩体抗弯、抗剪能力。现有文献中关于低承台管桩动力特性的研究主要为试验和数值研究,且忽略了土塞质量的影响,关于低承台管桩动力特性的理论研究几乎没有。鉴于此,本文基于广义Voigt模型及附加质量模型,考虑土塞质量,通过理论分析深入研究桩身参数、土塞、桩侧土及承台周围土体对低承台管桩纵向自由振动的影响规律,为桩基抗震减震设计提供一定的理论依据。
1 数学模型
承台-管桩-土系统相互作用模型如图1所示。根据桩侧土及土塞的成层性,将桩土系统划分为m层,其中土塞相应的划分为N层。将各层自管桩底部开始依次编号为1,2,…,j,…,N,…,m,各层厚度依次为l1,l2,…,lj,…,lN,…,lm,各层顶部深度依次为h1,h2,…,hj,…,hN,…,hm。

图1 承台-管桩-土系统相互作用模型
每层管桩材料为均质,截面尺寸相同,且桩土完全接触,变形为小变形,管桩桩长为H,外、内半径分别为r1,r2;采用附加质量模型模拟土塞与管桩之间的动态相互作用,即将各微元层内土塞的质量与管桩质量通过分布式Voigt模型连接在一起,分布式Voigt模型的弹簧系数和阻尼系数分别为kj,ηj;土塞高度为H1,第j层土塞的质量为mj;承台埋深为H2,承台底土对承台的支撑作用简化为单Voigt模型,该模型的弹簧系数和阻尼系数分别为kc,ηc;管桩底部为黏弹性支撑,即用单Voigt模型模拟桩端土对管桩的支撑作用,支撑刚度和阻尼分别为kb,ηb。根据Lymster等[20]的模拟计算公式可分别求得承台底部土体对承台的支撑刚度和阻尼以及桩端土对管桩的支撑刚度和阻尼
(1)
(2)
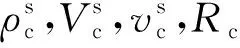
2 桩土系统振动方程及求解
2.1 承台-管桩系统侧土广义Voigt模型
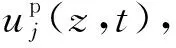
(3)


(4)
式中,Fs(s),U(s)分别为fs(t),u(t)关于时间t的Laplace变换式。
2.2 土塞及管桩自由振动控制方程及求解

土塞:
(5)

管桩:
(6)

桩土系统边界条件如下
管桩顶部:
(7)
式中,f(t)为管桩对承台的作用力。
管桩底部:
(8)
桩土系统连续条件如下
相邻管桩桩段接触面间的位移连续条件
(9)
相邻管桩桩段接触面间的截面力连续条件
(10)
桩土系统初始条件如下
管桩:
(11)
土塞:
(12)

(13)

式(13)是一个常系数一元二次微分方程,容易求解得
(14)
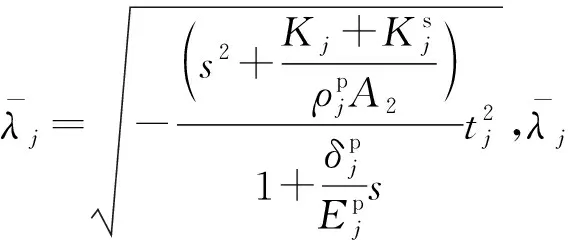
根据位移阻抗的定义,可以得到第1层管桩顶部的位移阻抗函数
(15)
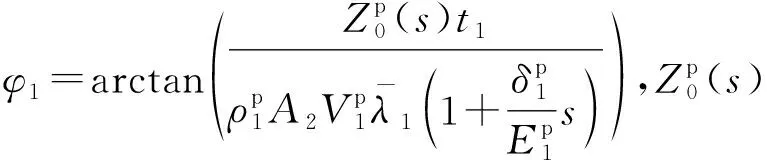
(16)
结合连续条件,利用阻抗函数传递方法,可得管桩顶部的位移阻抗
(17)

(18)

2.3 承台自由振动控制方程及求解
设承台为完全刚性体,根据承台的受力情况,可以建立承台自由振动控制方程如下
(19)
式中,M为承台质量,Ac=H2·2πRc为承台的侧表面积;承台埋深H2=0时,承台为明置,否则为埋置。
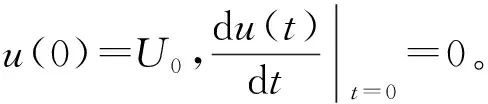
设F(s)为f(t)关于时间t的Laplace变换式,由位移阻抗的定义可得
(20)
结合承台的初始条件及式(4)、(20),对式(19)两边进行Laplace变换并简化得
U(s)=
(21)
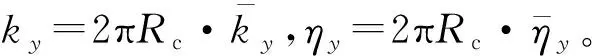
设s=iω,ω=2πf,i为虚数单位,f为常规意义上的频率,则承台的位移频响函数如下
U′(ω)=
(22)
对式(22)进行Laplace逆变换,可得承台的位移时域函数如下
u(t)=ITL(U(s))
(23)
3 附加质量模型中Voigt参数分析及退化验证
如无特殊说明,假设桩侧土及土塞为粉质黏土,承台侧土为回填土,则低承台-管桩-土系统参数取值如下:管桩参数:桩长10 m,外半径0.5 m,内半径0.4 m,纵波波速4 000 m/s,密度2 500 kg/m3;土塞参数:高度10 m,剪切波速200 m/s,密度1 800 kg/m3;桩侧土参数:剪切波速200 m/s,密度1 800 kg/m3,泊松比为0.35;承台参数:尺寸2 m×2 m×3 m,密度2 200 kg/m3,承台初始位移U0取无量纲值1;桩端土参数:密度为1 800 kg/m3,剪切波速为220 m/s,泊松比为0.35;承台侧土参数:密度为1 600 kg/m3,剪切波速为100 m/s;参考王奎华等[21]研究,桩土系统分层数m取值为100。
Wang等[22]提出可以用3个Voigt体串联的一维模型(如图1)近似的代替广义Voigt模型,相关参数的建议取值如下
(24)
式中,Gs=ρs·(Vs)2,Vs分别为相应土层的剪切模量和剪切波速,R为某点到z轴的距离,式(24)的相关参数取值为单位轴向长度的数值。
3.1 Voigt参数影响分析
与桩侧土相比,由于管桩内壁对土塞的约束,附加质量模型中的Voigt模型参数不能简单的按照连接桩侧土与管桩的动态Winkler模型参数来选取。为确定附加质量模型中的Voigt模型参数取值的敏感性区间,下面将分别讨论Voigt模型参数对低承台管桩纵向自由振动特性的影响。
附加质量模型中的Voigt模型参数上限区间可根据Randolph等[23]提出的桩侧土动态Winkler地基模型参数的经验公式k=2.7Gs/2πR,η=Gs/Vs计算,将本文土塞的参数代入上式可得:k=6.191×107N/m3,η=3.6×105N/m3·s,本文分析时附加质量模型中的Voigt模型参数的上限区间参考以上数值。基于附加质量模型的思想,吴文兵等通过模型桩试验,反演出管桩纵向振动时Voigt模型参数的取值,因此,本文分析时附加质量模型中的Voigt模型参数的下限区间参考吴文兵等反演出的参数,即k=7.85×105N/m3,η=1.53×105N/m3·s。
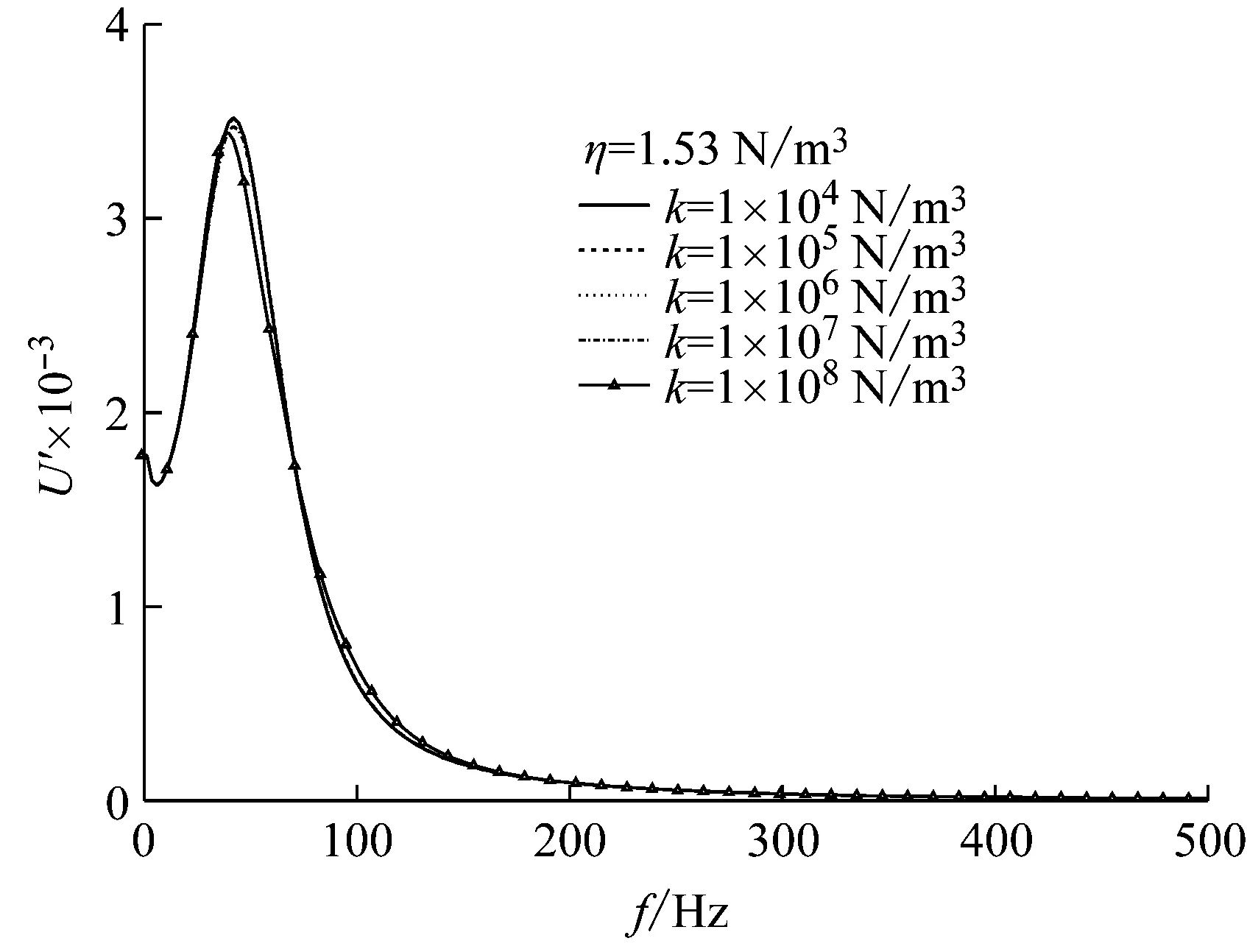
低承台桩基根据承台的埋深情况,可分为明置低承台桩基和埋置低承台桩基,为了更直观地分析附加质量模型中的Voigt模型参数对低承台管桩纵向自由振动特性的影响,首先,分析k对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响,η保持不变,即η=1.53×105N/m3·s,k分别取1×104,1×105,1×106,1×107,1×108N/m3。
由图2(a)、2(b)可知,当k在1×104~1×107N/m3变化时,明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线均趋于一致。当k大于1×107N/m3时,随着k的增大,明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的幅值均略幅减小。由此可见,k在区间1×104~1×107N/m3变化时,明置低承台管桩纵向自由振动特性稳定,与吴文兵等通过模型试验给出的结论接近。因此,后续分析中,k值设置为:k=7.85×105N/m3。
接下来分析η对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响,k保持不变,即k=7.85×105N/m3,η分别取1×105,2×105,3×105,4×105,5×105N/m3·s。
由图3(a)、3(b)可知,当η在1×105~3×105N/m3·s变化时,随着η的增大,明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线幅值均逐渐减小;当η大于3×105N/m3·s时,明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线均趋于一致。由此可见,η在区间3×105~5×105N/m3·s变化时,明置低承台管桩纵向自由振动特性稳定,与Randolph经验公式给出的数值接近。因此,后续分析中,η值设置为:η=3.6×105N/m3·s。
(a) 位移频域曲线

(b) 位移时域曲线
图2 Voigt模型参数k对明置低承台管桩纵向自由振动特性的影响
Fig.2 Influence ofkon the vertical free vibration of pipe pile with exposed low cushion cap
3.2 退化验证
陈鑫基于广义Voigt模型,求解出带承台实心桩纵向自由振动位移的时域半解析解,并采用现场试验验证了理论解的合理性。将本文解退化为实心桩解,即使管桩内径无限趋近于0,由图4可知,本文退化解与陈鑫解曲线基本吻合,验证了本文解的合理性。
4 明置低承台管桩参数分析
已有关于桩基动力特性的研究表明,桩长、桩径、桩侧土及土塞性质是影响桩基动力特性的重要因素,接下来分别分析桩长、桩径、桩侧土及土塞性质对低承台管桩纵向自由振动特性的影响。为直观地分析桩长、桩径、桩侧土及土塞性质对低承台管桩纵向自由振动特性的影响,如无特殊说明,本节不考虑承台侧土影响,即承台明置(即H2=0)。
4.1 桩身参数影响分析
4.1.1 桩长分析
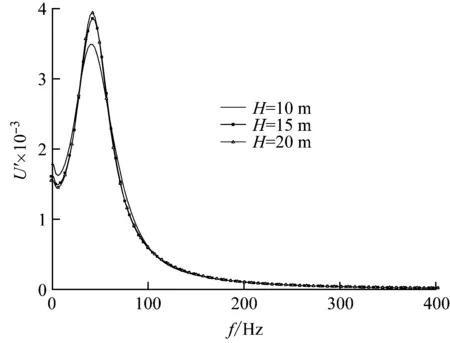
本小节分析了桩长对明置低承台管桩纵向自由振动特性的影响,桩长H取值如图5所示。

(a) 位移频域曲线

(b) 位移时域曲线
图3 Voigt模型参数η对明置低承台管桩纵向自由振动特性的影响
Fig.3 Influence ofηon the vertical free vibration of pipe pile with exposed low cushion cap
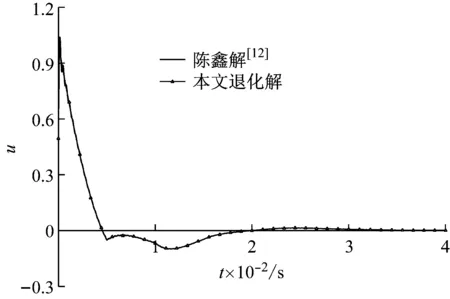
图4 本文解与陈鑫解的对比
图5(a)、5(b)分别反映了桩长对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。图5(a)反映了明置低承台管桩纵向自由振动位移频域曲线的幅值随着激振频率的增大总体呈先增大后逐渐衰减并趋于平稳的趋势。由图5(a)、5(b)可知,随着桩长的增大,位移频域曲线共振峰值逐渐增大,且增大的幅度逐渐减小;位移时域曲线的幅值呈先增大后逐渐趋于一致。为解释以上现象,可以将承台-管桩-土模型简化成简单的质弹阻模型,桩长增加导致质弹阻模型中的弹簧系数增大,在给予同样初始位移时,承台-管桩-土系统的初始能量越大;存在临界影响桩长Hc,当桩长小于临界影响桩长Hc时,因桩长增加引起的弹簧系数增大对明置低承台管桩的影响大于黏壶系数增大对明置低承台管桩纵向自由振动衰减的影响,位移频域曲线的共振峰峰值及位移时域曲线的幅值随桩长的增加均逐渐增大;当桩长达到临界影响桩长Hc时,黏壶系数已足够大,使桩身波动能量传递到桩身Hc处完全消散,因此随着管桩桩长的继续增加,明置低承台管桩纵向自由振动位移时域曲线的幅值不再增大。
(a) 位移频域曲线

(b) 位移时域曲线
Fig.5 Influence of the length of pipe pile on the vertical free vibration of pipe pile with exposed low cushion cap
以上现象表明,在实际工程中,考虑经济性的情况下,低承台管桩桩长应小于临界桩长。本文研究工况下,桩长设置为H=10 m较为合适。
4.1.2 桩径分析
本小节分析了桩径对明置低承台管桩纵向自由振动特性的影响,桩径影响分析可以从两个方面展开:①壁厚不变,同时增大或减小管桩的内外半径;②管桩内半径或外半径不变,增大管桩壁厚。管桩内外半径取值如图6所示。
图6(a)、6(b)分别反映了管桩桩径对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图6(a)、6(b)可知:随着管桩壁厚增大,即管桩内半径减小或外半径增大,位移频域曲线的共振峰峰值和位移时域曲线的幅值均减小,但管桩外半径增大造成的影响要大于管桩内半径减小造成的影响;管桩壁厚不变,随着管桩内、外半径的同时减小,位移频域曲线的共振峰峰值和位移时域曲线的幅值均增大。以上现象前者表明桩侧土对低承台管桩动力特性的影响要大于土塞对低承台管桩动力特性的影响;后者的作用机理与临界影响桩长内桩长影响的作用机理一致。

(a) 位移频域曲线

(b) 位移时域曲线
Fig.6 Influence of the radius of pipe pile on the vertical free vibration of pipe pile with exposed low cushion cap
由以上现象可知,在桩基动力设计中,可以通过增大管桩壁厚或采用壁厚相同半径较大的管桩来增强低承台管桩系统的抗震性能。
4.2 土塞性质影响分析
已有研究表明,土塞高度和密度对管桩的动力特性有明显影响,本小节分别分析了土塞高度和密度对低承台管桩纵向自由振动特性的影响。
4.2.1 土塞高度分析
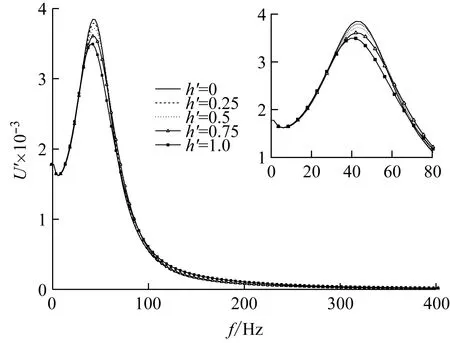
定义土塞高度与管桩桩长比为h′,h′越大,土塞高度越大,h′取值如图7所示。
图7(a)、7(b)分别反映了土塞高度对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图7(a)可知,明置低承台管桩纵向自由振动位移频域曲线有一个共振峰,随着土塞高度的增大,共振峰峰值逐渐减小,共振频率逐渐前移。由图7(b)可知,随着土塞高度的增大,明置低承台管桩位移时域曲线幅值逐渐减小。随着土塞高度的增大,土塞对管桩的阻碍作用增大,致使明置低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值均逐渐减小。
(a) 位移频域曲线

(b) 位移时域曲线
Fig.7 Influence of the height of soil plug on the vertical free vibration of pipe pile with exposed low cushion cap
4.2.2 土塞密度分析
定义土塞密度与桩侧土密度比为ρ′,ρ′大于1时,表示土塞硬化现象;ρ′小于1时,表示土塞软化现象,ρ′取值如图8所示。
图8(a)、8(b)分别反映了土塞密度对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图8(a)可知,随着土塞密度的增大,位移频域曲线共振峰峰值逐渐减小。由图8(b)可知,随着土塞密度的增大,位移时域曲线幅值逐渐减小。随着土塞密度的增大,土塞的质量增大,土塞对明置低承台管桩系统的能量耗散作用增强,因此明置低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值均逐渐减小。
综合上述4.2.1节和4.2.2节分析可得,在低承台管桩基础施工的过程中,可以通过将管桩内部土塞填满并加固来增强低承台管桩基础的抗震性能。

(a) 位移频域曲线

(b) 位移时域曲线
Fig.8 Influence of the density of soil plug on the vertical free vibration of pipe pile with exposed low cushion cap
4.3 桩侧土性质影响分析
4.3.1 桩侧土剪切波速分析
首先分析桩侧土剪切波速对明置低承台管桩纵向自由振动特性的影响,其中Vs3表示桩侧土剪切波速,取值如图9所示。
图9(a)、9(b)分别反映了桩侧土剪切波速对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图9(a)可知,当桩侧土剪切波速较小时,明置低承台管桩纵向自由振动位移频域曲线有两个共振峰,随着桩侧土剪切波速的增大,共振峰逐渐变为一个且共振峰峰值逐渐减小,共振频率逐渐后移。
由图9(b)可知,随着桩侧土剪切波速的增大,明置低承台管桩纵向自由振动位移时域曲线的幅值呈现增大的趋势,位移幅值点逐渐前移。以上现象可以解释为:随着桩侧土剪切波速的增大,桩侧土模型的弹簧系数和阻尼系数同时增大;桩侧土模型弹簧系数的增大,会使具有相同初始位移的承台所具有的初始能量越大;桩侧土模型阻尼系数的增大,会使承台管桩基础的能量衰减作用变大,但该衰减作用小于弹簧常数所造成的影响。总的来说,明置低承台管桩纵向自由振动位移时域曲线的幅值随着桩侧土剪切波速的增大逐渐增大。当Vs3=50 m/s时,明置低承台管桩纵向自由振动位移时域曲线表现出波传递的性质,在2H/vp时刻左右承台会产生一个波动。

(a) 位移频域曲线

(b) 位移时域曲线
图9 桩侧土剪切波速对明置低承台管桩纵向自由振动特性的影响
Fig.9 Influence of shear wave velocity of pile surrounding soil on the vertical free vibration of pipe pile with exposed low cushion cap
4.3.2 桩侧土密度分析
接下来分析桩侧土密度对明置低承台管桩纵向自由振动特性的影响,ρs3表示桩侧土密度,取值如图10所示。
图10(a)、10(b)分别反映了桩侧土密度对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图10(a)可知,明置低承台管桩纵向自由振动位移频域曲线有一个共振峰,随着桩侧土密度的增大,共振峰峰值逐渐减小,共振频率逐渐后移。
由图10(b)可知,随着桩侧土密度的增大,明置低承台管桩位移时域曲线幅值逐渐增大,位移幅值点逐渐前移。以上现象与图9(b)规律一致且作用机理基本相同,但桩侧土密度对明置低承台管桩纵向自由振动特性的影响要小于桩侧土剪切波速造成的影响,这是由于桩侧土模型的弹簧系数与剪切波速的平方成正比,与密度成正比。
综合4.3.1节和4.3.2节现象,可以看出:桩侧土层越软,低承台管桩基础纵向自由振动的共振频率越低,但共振峰峰值越大;在半正弦激振荷载作用下,激振频率一定时,在软土层中,低承台管桩的抗震性能较强。

(a) 位移频域曲线

(b) 位移时域曲线
Fig.10 Influence of density of pile surrounding soil on the vertical free vibration of pipe pile with exposed low cushion cap
4.4 承台底土性质影响分析
与无承台管桩基础相比,承台的存在使得低承台管桩与土之间的相互作用变得更加复杂,低承台管桩不仅受管桩内土塞和桩侧土的约束,还受承台底部土体和承台侧土的约束。
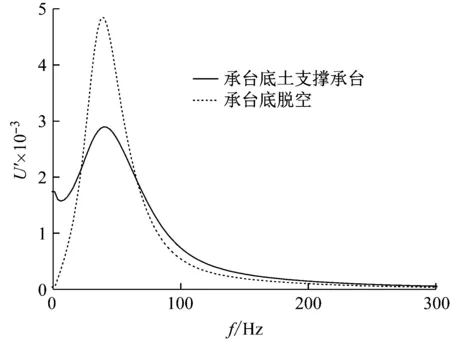
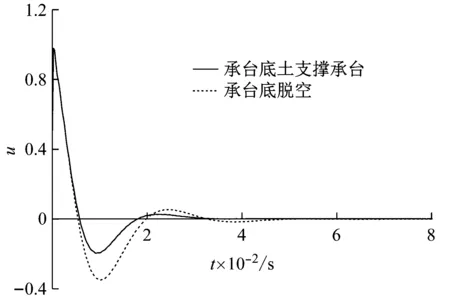
在带承台桩基静力特性研究中,已有试验研究表明,若在承台底面铺垫一定厚度的碎石层并经适当碾压,可以大大提高承台分担荷载的能力,从而提高承台桩基的极限承载能力[24-25],即说明承台底土的性质对承台的荷载分担能力有明显影响。在动力荷载作用下,承台底部土体对低承台管桩基础纵向自由振动特性可能也有类似的影响,为了直观地分析承台底土对低承台管桩纵向自由振动特性的影响,本节分析忽略承台侧土,即将低承台完全退化为明置承台(H2=0)。首先,将本文解退化为承台底土对承台有支撑作用和无支撑作用(即承台底面脱空)两种情况进行对比分析。图11为承台底土对承台有无支撑作用的对比图,结果表明,承台底土的支撑作用对明置低承台管桩纵向自由振动特性有较大影响。接下来,从承台底土的剪切波速和密度两方面来分析承台底土对明置低承台管桩纵向自由振动特性的影响。
(a) 位移频域曲线
(b) 位移时域曲线
Fig.11 Influence of soil under cushion cap on the vertical free vibration of pipe pile with exposed low cushion cap
4.4.1 承台底土剪切波速分析
分析承台底土剪切波速对明置低承台管桩纵向自由振动特性的影响时,Vs1表示第m层桩侧土剪切波速,取值如图12所示。
图12(a)、12(b)分别反映了承台底土剪切波速对明置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图12(a)可知,明置低承台管桩纵向自由振动位移频域曲线存在一个共振峰,随着承台底土剪切波速的增大,共振峰峰值逐渐减小,共振频率基本保持不变。当激振频率远离共振频率时,随着承台底土剪切波速的增大,明置低承台管桩纵向自由振动位移值逐渐增大。
由图12(b)可知,随着承台底土剪切波速的增大,明置低承台管桩纵向自由振动位移时域曲线幅值逐渐减小,位移幅值点逐渐前移。以上现象可作如下解释:随着承台底土剪切波速的增大,承台底土模型弹簧系数和阻尼系数同时增大;由于单桩承台底部土层对承台的支撑作用小于桩身、桩侧土及桩端土共同对承台的支撑作用,在给予承台相同的初始位移时,承台底土模型弹簧系数的增大几乎不改变承台的初始能量;但随着承台底土模型弹簧系数和阻尼系数的同时增大,承台底土对承台的支撑刚度增大,且承台底土对明置低承台管桩的能量耗散作用也增大,最终导致明置低承台管桩纵向自由振动位移幅值逐渐减小,位移幅值点逐渐前移。
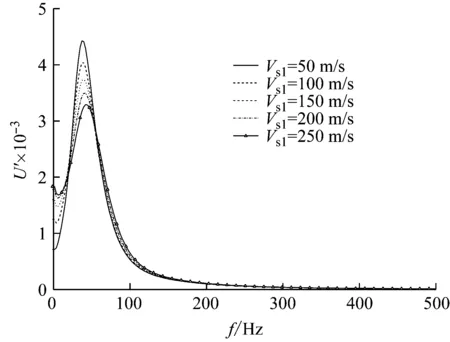
(a) 位移频域曲线

(b) 位移时域曲线
图12 承台底土剪切波速对明置低承台管桩纵向自由振动特性的影响
Fig.12 Influence of shear wave velocity of soil under cushion cap on the vertical free vibration of pipe pile with exposed low cushion cap
4.4.2 承台底土密度分析
接下来,分析承台底土密度对明置低承台管桩纵向自由振动特性的影响,ρs1表示第m层桩侧土密度,取值如图13所示。
由图13可知,承台底土密度对明置低承台管桩纵向自由振动特性的影响与承台底土剪切波速所造成的影响规律一致,作用机理也基本相同,但剪切波速造成的影响更明显。这是由于承台底土模型弹簧系数与剪切波速的平方成正比,与密度成正比。
由以上分析可得,承台底土越硬,明置低承台管桩的抗震性能越强。因此,在工程实践中,可以通过在承台底部铺设一定厚度的碎石层并经适当碾压,来增大低承台管桩基础的抗震性能。

(a) 位移频域曲线
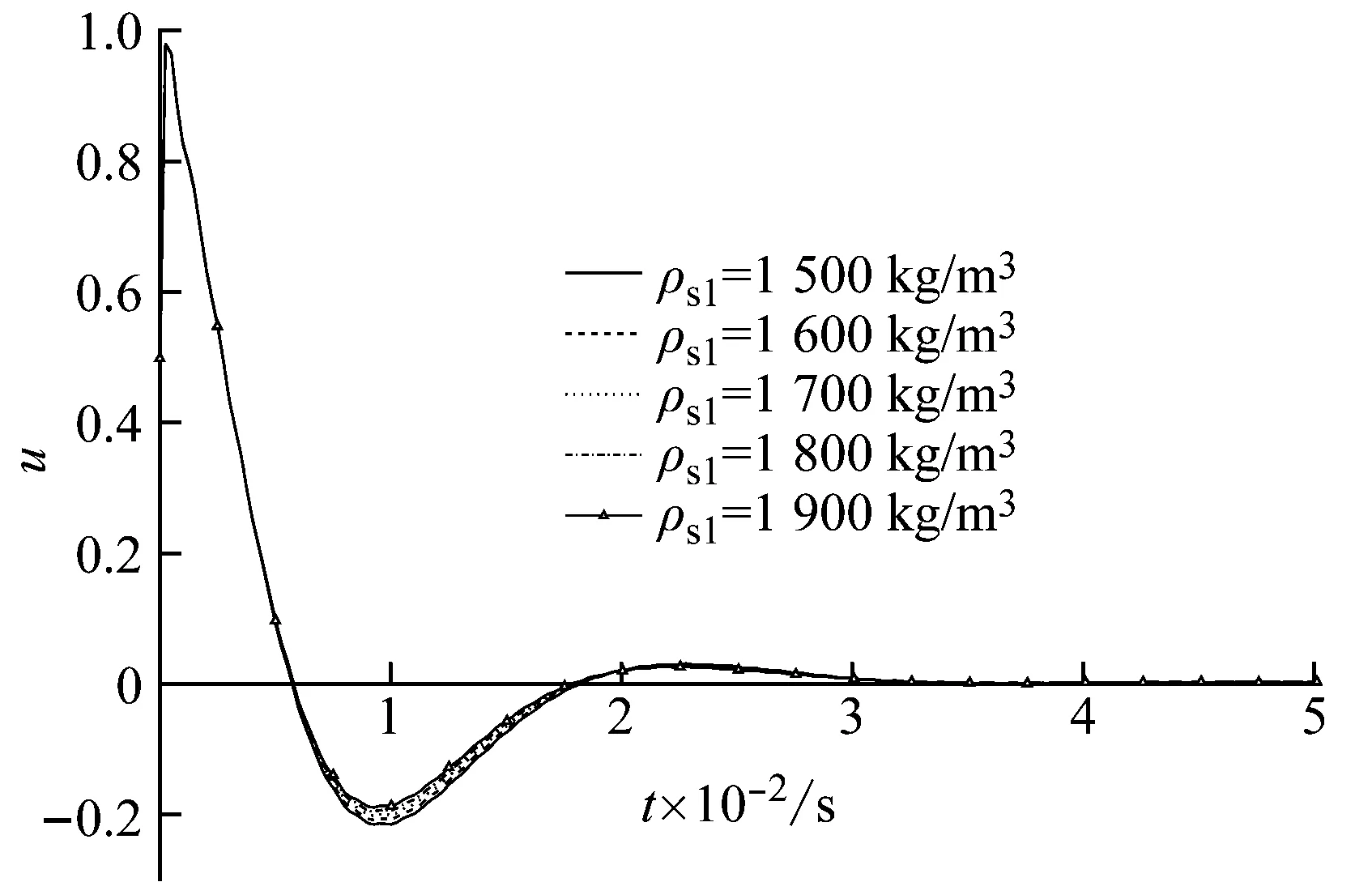
(b) 位移时域曲线
图13 承台底土密度对明置低承台管桩纵向自由振动特性的影响
Fig.13 Influence of density of soil under cushion cap on the vertical free vibration of pipe pile with exposed cushion cap
5 埋置低承台管桩参数分析
5.1 承台埋深影响分析
为研究承台侧土对低承台管桩纵向自由振动特性的影响,本节分析埋置承台,即0 m 由图14(b)可知,随着承台埋深的增大,埋置低承台管桩纵向自由振动位移时域曲线幅值逐渐减小,位移幅值点逐渐前移。以上现象的产生可以解释为:随着承台埋深的增大,承台侧土对承台的阻碍作用逐渐增大,使得埋置承台管桩纵向自由振动位移幅值逐渐减小。由以上分析可知,承台侧土对埋置低承台管桩纵向自由振动特性有明显影响。 (a) 位移频域曲线 (b) 位移时域曲线 Fig.14 Influence of buried depth of cushion cap on the vertical free vibration of pipe pile with buried low cushion cap 进一步,从承台侧土的剪切波速和密度两方面来分析承台侧土性质对埋置低承台管桩纵向自由振动特性的影响。为了更直观地分析承台侧土对埋置低承台管桩纵向自由振动特性的影响,本节分析全埋置承台,即H2=3 m。 5.2.1 承台侧土剪切波速分析 分析承台侧土剪切波速对埋置低承台管桩纵向自由振动特性的影响时,Vs2表示承台侧土剪切波速,取值如图15所示。 图15(a)、15(b)分别反映了承台侧土剪切波速对埋置低承台管桩纵向自由振动位移频域曲线和位移时域曲线的影响。由图15(a)可知,随着承台侧土剪切波速的增大,位移频域曲线共振峰峰值逐渐减小,共振频率保持不变。 由图15(b)可知,随着承台侧土剪切波速的增大,埋置低承台管桩纵向自由振动位移时域曲线幅值逐渐减小,位移幅值点逐渐前移。以上现象可作如下解释:随着承台侧土的剪切波速增大,承台侧土对承台的作用系数逐渐增大(由式(3)可知),导致承台侧土与承台的相互作用增大,进而使埋置低承台管桩纵向自由振动位移时域曲线幅值逐渐变小。 (a) 位移频域曲线 (b) 位移时域曲线 图15 承台侧土剪切波速对埋置低承台管桩纵向自由振动特性的影响 Fig.15 Influence of shear wave velocity of soil surrounding cushion cap on the vertical free vibration of pipe pile with buried low cushion cap 5.2.2 承台侧土密度分析 分析承台侧土密度对埋置低承台管桩纵向自由振动特性的影响时,ρs2表示承台侧土剪切波速,取值如图16所示。由图16可知,承台侧土密度对埋置低承台管桩纵向自由振动特性的影响与承台侧土剪切波速所造成的影响规律一致,作用机理也基本一致;但剪切波速的影响更为明显,这是由于承台侧土模型弹簧系数与剪切波速的平方成正比,与密度成正比。 综合上述分析可得,在低承台管桩基础的施工过程中,可以通过使承台完全埋置并对承台侧土进行加固处理来增强低承台管桩基础的抗震性能。 本文基于广义Voigt模型及附加质量模型,系统的研究了桩身参数、土塞、桩侧土及承台周围土体对低承台管桩纵向自由振动特性的影响规律,研究结果表明: (1) 本文退化解与实心桩解对比,验证了本文解的合理性,为管桩基础的动力检测和抗震减震设计提供了新的理论依据。 (a) 位移频域曲线 (b) 位移时域曲线 图16 承台侧土密度对埋置低承台管桩纵向自由振动特性的影响 Fig.16 Influence of density of soil surrounding cushion cap on the vertical free vibration of pipe pile with buried low cushion cap (2) 低承台管桩基础存在一个临界影响桩长,当桩长小于该临界影响桩长时,随着桩长的增大,明置低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值均逐渐增大;当桩长超过这个临界影桩响长时,桩长的增大对低承台管桩纵向自由振动特性无明显影响。 (3) 桩侧土对低承台管桩动力特性的影响要大于土塞对低承台管桩动力特性的影响;桩侧土越软,低承台管桩基础的抗震性能越强。 (4) 土塞质量对低承台管桩纵向自由振动特性有明显影响。随着土塞高度或密度的增大,低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值均逐渐减小,因此可以通过将管桩内部土塞填满并夯实来增强低承台管桩基础的抗震性能。 (5) 承台底土剪切波速的增大或密度的增大均会使低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值逐渐减小,从理论上验证了在承台底部铺设一定厚度的碎石层并经适当碾压,可以增大低承台管桩基础的抗震性能。 (6) 低承台管桩纵向自由振动位移频域曲线的共振峰峰值和位移时域曲线的幅值均会随着承台的埋深、承台侧土的密度及剪切波速的增大而减小,因此,为提高低承台管桩基础的抗震性能,在施工过程中,采用回填土将承台完全埋置并对承台侧土进行加固处理是十分有必要的。

5.2 承台侧土性质影响分析
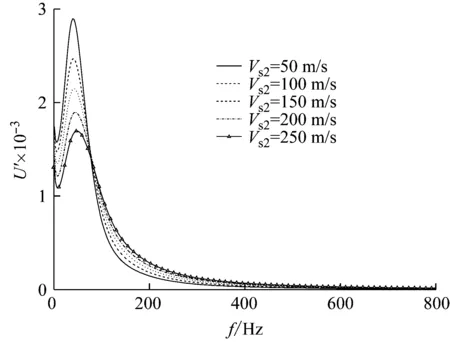

6 结 论



