基于硬涂层的主动失谐整体叶盘建模与分析
高俊男, 孙 伟
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.东北大学 航空动力装备振动及控制教育部重点实验室,沈阳 110819)
整体叶盘是通过先进的制造工艺将叶片与轮盘做成一体,具有结构简单、重量轻和性能优越的特点,已在各型号航空发动机中广泛应用。叶盘结构理论上是循环对称结构,但通常因为制造误差、不均匀磨损等原因而发生失谐[1]。失谐破坏了叶盘结构的循环对称性,导致结构出现振动局部化[2-4],造成少数叶片振幅和应力水平显著增大,致使结构过早出现高周疲劳失效。因此,研究如何降低或抑制失谐造成的结构振动水平过大问题十分重要。
主动失谐设计作为抑制叶盘振动的重要方法近年来被广泛研究。Castanier等[5]基于CMS方法发现将主动失谐引入叶盘后可以降低失谐叶盘的响应水平以及结构对失谐的敏感性。之后Castanier等[6]采用集中参数模型,将叶片的弹性模量作为失谐变量,研究了不同主动失谐模式下结构受迫振动的统计规律,得出某些特定的主动失谐模式可以显著减小结构的振动响应水平并且大大降低结构对失谐的敏感性。Hou等[7]同样以叶片弹性模量作为失谐变量,基于集中参数模型优化了主动失谐模式,使得各叶片的响应水平均明显降低。于长波等[8]通过ANSYS的超单元方法建立了压气机叶盘的有限元减缩模型,以叶片型面厚度作为失谐变量,得出随着失谐程度增加系统的响应水平和其分散程度都会存在一个峰值。段勇亮等[9]将叶片固有频率失谐作为设计参数,研究了常见的几种主动失谐形式下叶盘的响应特性和对随机失谐的鲁棒性,得出主动失谐设计具有较为明显的减振效果和鲁棒性。
除了主动失谐设计,阻尼减振也是抑制叶盘结构振动的一种重要方式。大量的减振技术,包括摩擦阻尼[10-13]、压电阻尼[14-15]、颗粒阻尼[16]、约束层阻尼[17]等均在叶盘结构减振上进行了实践。除此之外,美国NASA[18]相关研究人员还提出在整体叶盘上(主要是叶片)上涂敷硬涂层来有效地抑制整体叶盘的过大振动。硬涂层是由金属基与陶瓷基或两者的混合制成的涂层材料,其作为减振应用最大的技术优势就是其可以在高温、高腐蚀环境下保持应有的阻尼能力。因此,叶盘的硬涂层减振是一项非常具有应用前景的减振技术。
目前整体叶盘的主动失谐主要依靠加工制造来实现,成本高且制造难度大。而通过在各个扇区叶片上涂敷不同厚度的硬涂层阻尼材料可以方便地构造主动失谐,并且同时起到阻尼减振作用。硬涂层构造的主动失谐包含了刚度、质量主动失谐,与此同时还会引起阻尼失谐。为了分析该主动失谐方法特性以及更好地应用该方法,必须建立一个基于硬涂层的主动失谐整体叶盘动力学模型来分析结构的动力特性。
迄今,关于利用硬涂层来构建整体叶盘的主动失谐文献资料很少,因此本文尝试性地以简化的失谐叶盘结构为研究对象,首先给出由单扇区模型构建失谐叶盘结构矩阵的方法,然后根据单变量函数的泰勒展开和最小二乘法建立硬涂层涂敷厚度与其造成的失谐矩阵的近似关系。再根据公称模态子集法建立了基于硬涂层的主动失谐整体叶盘减缩模型。在此基础上,将硬涂层涂敷厚度作为失谐参数,并结合Monte Carlo模拟研究了基于硬涂层的主动失谐叶盘振动特性。最后,分析了该主动失谐方法的减振效果以及减振特点。
1 减缩模型与响应求解
本文的减缩模型主要依据公称模态子集(SNM)方法[19]构建。在失谐较小的情况下,失谐叶盘的振型可由谐调叶盘振型的线性组合近似。因此,可由截断的谐调模态集对失谐的结构矩阵进行降阶。因为降阶后的矩阵是非对角的,需要将结构的动力方程转换到状态空间解耦求解,具体建模流程如图1所示。

图1 减缩建模方法流程
1.1 主动失谐叶盘结构矩阵
主动失谐叶盘的结构矩阵可由谐调叶盘的结构矩阵、叶盘的随机失谐矩阵和叶盘的主动失谐矩阵这三部分构成,且三部分都能以扇区的形式描述。单扇区模型如图2所示,其可分成交界面t与p和扇区内部g,同时扇区内部g又可以分为轮盘d和叶片b。
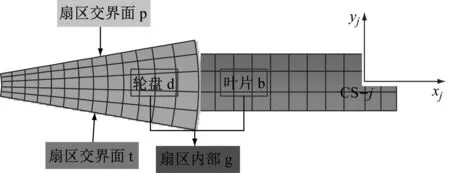
图2 单个扇区模型
1.1.1 谐调叶盘矩阵
谐调叶盘的单个扇区结构矩阵可从ANSYS、Nastran等商业有限元软件中提取。将扇区刚度矩阵kS(扇区质量矩阵mS的形式相同)按图2中的交界面t的节点自由度、扇区内部g的节点自由度和交界面p的节点自由度排序,则可以写成以下的分块形式
(1)
本文提取的矩阵是在直角坐标系(例如图2中的扇区坐标系CS-j)下建立的,因此有相邻扇区交界面的位移协调条件为
xjp=Rx(j+1)t
(2)
式(2)中xjp表示第j扇区交界面p的位移,转换矩阵R表示将扇区交界面位移由当前扇区坐标系下描述转换到前一扇区坐标系下描述。将式(2)的位移协调条件扩展到整个叶盘有
(3)
式中,N表示叶盘的扇区数。于是由式(3)得到,谐调叶盘的刚度和质量矩阵为
(4)
1.1.2 叶盘随机失谐矩阵

(5)
式中,δj为表示第j扇区叶片失谐程度的随机数,kbb代表谐调叶盘单个叶片的刚度。

(6)
其中,
(7)
因此,与式(4)同理,叶盘的随机刚度失谐矩阵ΔKr有以下形式
(8)
1.1.3 叶盘主动失谐矩阵
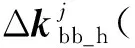
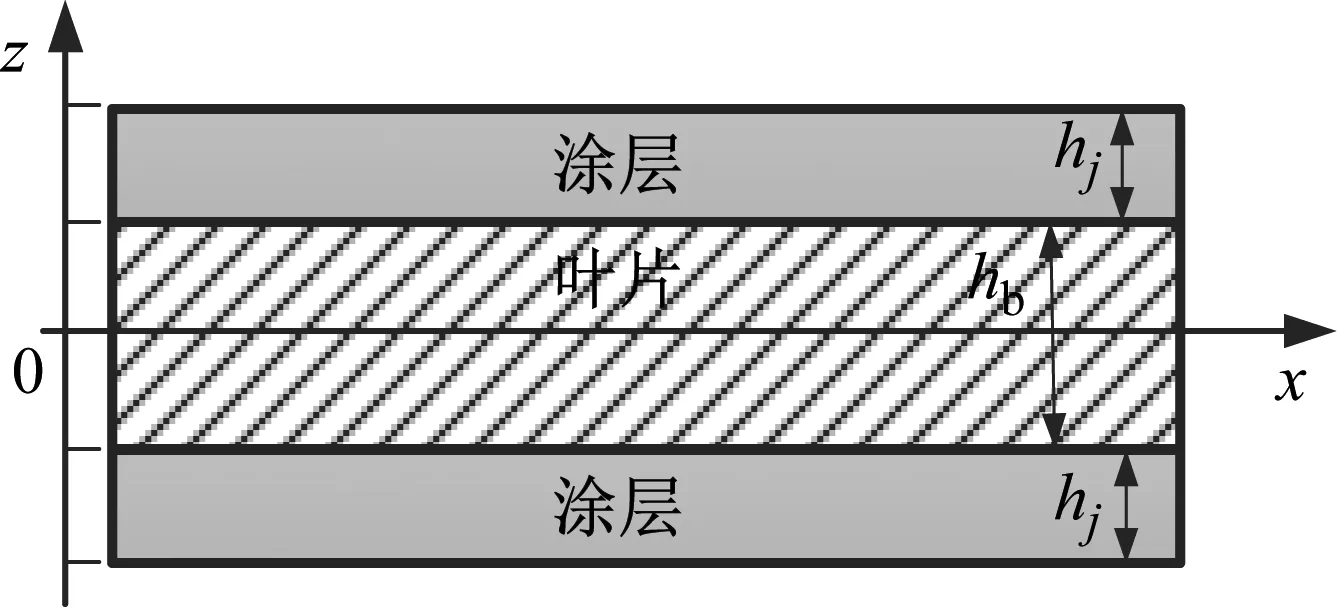
图3 涂敷硬涂层叶片的部分截面
(9)
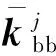
在决定每个叶片上的硬涂层涂敷厚度时,通常需要对比很多涂敷方案(例如式(33)的方案,各叶片涂敷厚度按一次谐波变化)。而当涂敷方案变化时,如果通过式(9)来计算涂层引起的各叶片的失谐刚度与失谐质量,则需要重建各个扇区的涂层叶片的有限元模型。这个过程是极其低效的,因此需要建立一个适用于不同涂敷方案的通用计算公式。
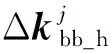
(10)
(11)
要解出式(11)的系数矩阵,可以事先提取r个涂敷不同厚度硬涂层的叶片的刚度矩阵并代入式(9),得到r个失谐刚度。将这r个厚度与失谐刚度代入式(11),于是可将式(11)系数矩阵的求解转化为标准最小二乘问题,如下式
(12)
式中,
(13)
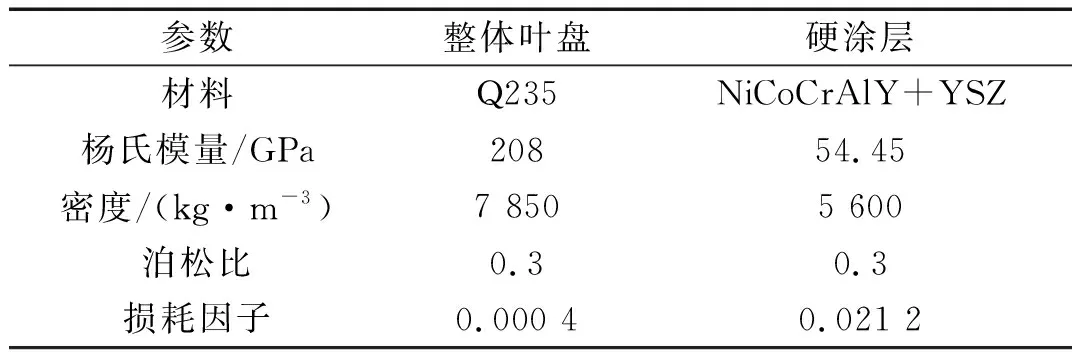
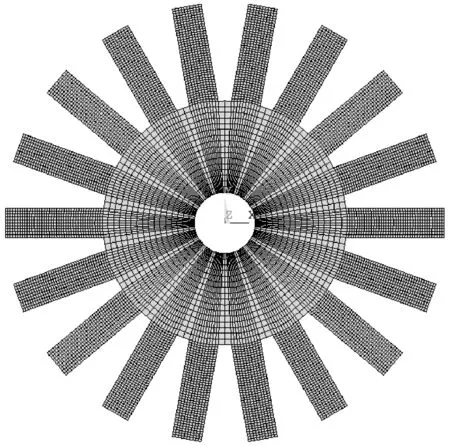
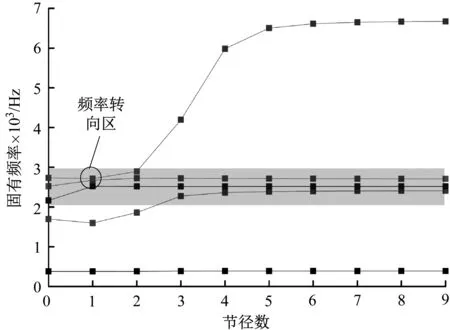
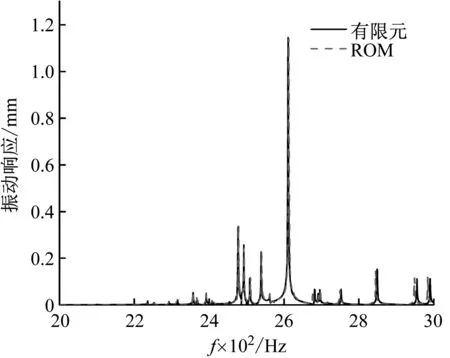
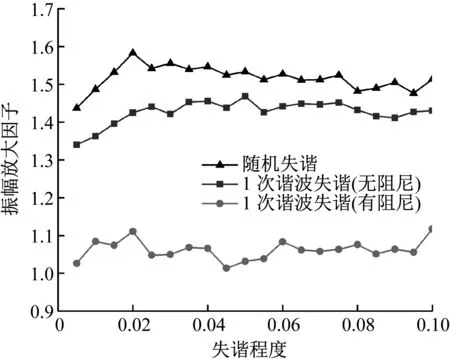
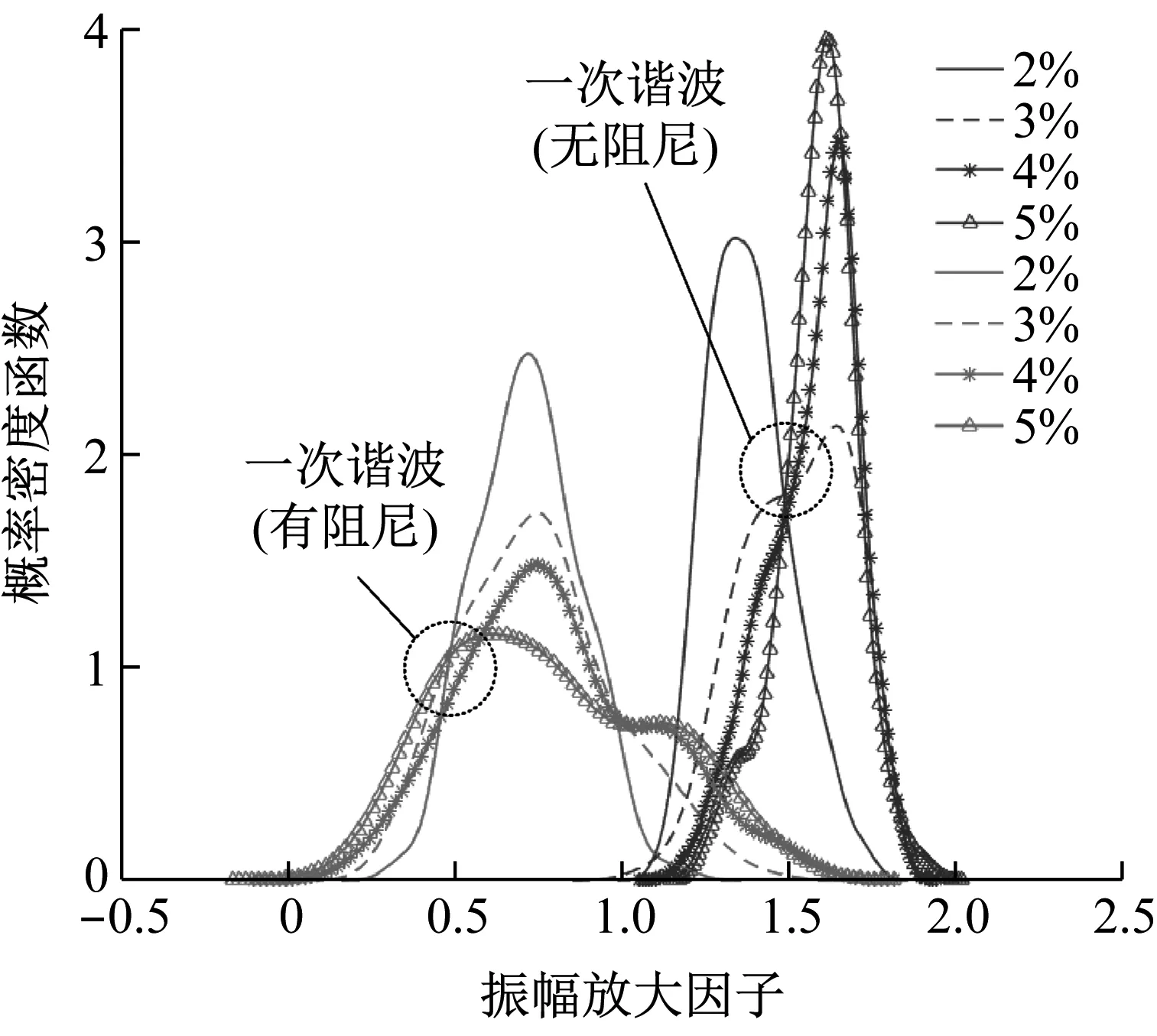
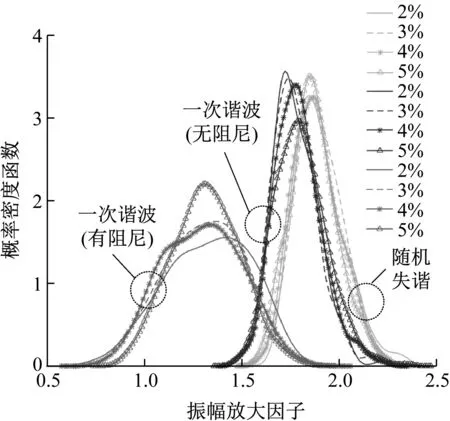
0 (14) 若h的各列线性无关,则系数矩阵为 (15) 因此,对于任意涂敷厚度hj(0≤hj≤hjr)所引起的叶片失谐刚度(失谐质量同理)都可通过式(11)近似计算。 (16) 式中, (17) 与式(4)同理,涂层引起叶盘的失谐刚度ΔKh(失谐质量ΔMh也类似)有以下形式 (18) 涂层引起的叶盘失谐刚度ΔKh和失谐质量ΔMh即叶盘的主动失谐矩阵。 这里将叶盘和涂层的阻尼考虑为材料阻尼以复刚度的形式引入,于是主动失谐叶盘结构的受迫振动方程可以写成 (K+ΔKh+ΔKr)x-ω2(M+ΔMh)x+ i(ηhΔKh+ηbΔKr+ηbK)x=f (19) (20) 其中, (21) 谐调叶盘的模态也可通过单扇区模型计算得到,参照文献[20-21]。将式(20)代入式(19)得到减缩后的结构受迫振动方程 (22) 其中, (23) 将式(22)写成状态空间形式 (-A+iωB)y=q (24) 其中, (25) (26) (27) 令状态空间方程(24)的左、右特征矩阵分别为L和γ。 L=[l1,l2,…,l2n],γ=[r1,r2,…,r2n] (28) 将状态向量y写成如下形式 (29) 将式(29)代入式(24)并左乘LH,得到 (-a+iωb)z=LHq (30) 其中, (31) 由式(30)、(31)解得z。状态空间右特征矩阵γ由位移和速度两部分构成 (32) 于是结构位移响应x可以表示为 (33) 叶盘结构在实际运行中叶片受到流场激励,可表示为不同阶次行波的叠加形式。因此,整个叶盘所受的激励可以表示为 f=eC⊗(Aeiωt) (34) (35) 式中,A为1号叶片受到激励的幅值向量,ω为激励频率,N为扇区数,C表示行波激励的阶次。 本文以简化的整体叶盘为例,其叶片厚度(不包含硬涂层厚度)和轮盘厚度分别为3 mm和15 mm,其有限元模型如图4所示。采用Shell181单元对模型进行网格划分,叶片部分采用多层单元而轮盘部分用单层单元,同时轮盘的内孔表面加上位移约束。该模型共有10 656个单元、11 592个节点,硬涂层和叶盘的材料参数见表1,对应该模型的谐调叶盘的节径频率图如图5所示。 表1 硬涂层整体叶盘材料参数 图4 简化整体叶盘 图5 节径频率图 方便起见,这里将每个叶片所受的激励简化为叶尖的单位激励。在C次行波激励下,理想的谐调叶盘结构各叶片的振幅是相等的,相邻叶片的振动相位相差Cθ。当失谐后,结构会出现振动局部化现象,振动只发生在少数或单个叶片上且振幅大幅增加。因此,这里定义失谐叶盘的振幅放大因子χ (36) 式中,xmistune表示失谐叶盘叶片的最大位移响应,xtune表示谐调叶盘叶片的最大位移响应。实际中叶片的随机失谐通常都在一个特定范围内,因此这里令式(5)中δj的服从均值为0,标准差分别为0~10%,取值范围为[-0.2,0.2]的双侧截尾正态分布[22]。 将涂层涂敷厚度hj作为主动失谐的参数,这里只研究各扇区的叶片涂敷厚度按一次谐波规律变化,如下式 hj=hS(cos[(j-1)θ]+1) (37) 通常SNM方法不适用于失谐程度较大的叶盘,因此为了验证式(11)的近似方法的准确性以及在该模型上使用SNM减缩方法(ROM)的合理性,这里令随机失谐标准差为10%和hS=0.2 mm,分别用减缩方法和完整有限元(FEM)模型计算了1次行波激励下计算了在第一弯曲模态族频率区间响应最大的叶尖以及第一频率转向区(如图5)频率区间1号叶片叶尖的振动响应见图6。从图中可以看出减缩模型和完整有限元模型计算的计算结果几乎相同,表明减缩模型和引入的近似方法都具有较高的计算精度。 (a) 第一模态族频率区间 (b) 第一频率转向频率区间 硬涂层构造的主动失谐会引起叶盘的阻尼失谐,而阻尼失谐会增加受迫振动响应[23],因此需要计算硬涂层含材料阻尼和不含材料阻尼两种情况。 这里令hS=0.15 mm(以下所有结果都是基于该值进行计算),然后应用Monte Carlo模拟来研究硬涂层构造的主动失谐叶盘的响应特性,模拟样本300次计算得到在一弯模态族频率范围内失谐程度(标准差)与振幅放大因子(其90%分位数)之间的关系曲线如图7、图8所示。 图7 失谐叶盘响应放大因子(C=1) 图8 失谐叶盘响应放大因子(C=9) 与文献[6]相似,随机失谐叶盘结构的振幅放大因子都会随着失谐程度的增加先增加再减小。对于基于硬涂层构造的1次谐波主动失谐叶盘,当硬涂层不含阻尼时结构的振幅放大因子随失谐程度的增加先增加再减小但相较于随机失谐叶盘要小,但当硬涂层含阻尼时结构的振幅放大因子明显减小同时不再表现出随着失谐程度先增大再减小的规律。 图9(a)给出了一次行波激励下随机失谐叶盘和基于硬涂层(不含阻尼时)构造的一次谐波主动失谐叶盘的振幅放大因子的概率密度函数(图中的不同线型分别对应不同的标准差)。从中可以看出:主动失谐叶盘的概率密度函数曲线在随机失谐叶盘的左侧并且相比随机失谐更高更窄,表明在该激励下基于硬涂层(不含阻尼时)构造的主动失谐能在降低随机失谐下叶盘结构的响应水平的同时还能降低对失谐的敏感性。 (a) 随机失谐与主动失谐叶盘对比(C=1) (b) 主动失谐叶盘间对比(C=1) (c) 随机失谐与主动失谐叶盘对比(C=9) Fig.9 Probabilistic density function of response magnification factors of the detuned blisk 图9(b)给出了一次行波激励下硬涂层含阻尼和不含阻尼时基于其构造的一次谐波主动失谐叶盘振幅放大因子的概率密度函数。可以看出硬涂层含阻尼时的概率密度函数曲线位于不含阻尼时的左侧,表明当硬涂层含阻尼时结构的响应水平会进一步降低,表现出了硬涂层的阻尼减振作用。同时结合图8不难看出硬涂层的阻尼减振的效果好于其构造的主动失谐(刚度与质量的主动失谐)的减振效果。但是当硬涂层含阻尼后其概率密度函数曲线变得更宽更矮,表明结构的振幅当大因子分布更分散了即结构对失谐的敏感性增大了,这一现象说明扇区间的阻尼失谐会增加结构对失谐的敏感性。 图9(c)给出了9次行波激励下随机失谐叶盘以及当硬涂层含阻尼和不含阻尼时基于其构建的主动失谐叶盘振幅放大因子的概率密度函数。可以发现:与1次行波激励下相同的是,当硬涂层含阻尼时其构造的主动失谐可以明显降低结构响应水平,其中也是硬涂层阻尼起到主要减振作用,同时其对应的振幅放大因子也更分散了。与1次行波激励下不同的是当硬涂层不含阻尼时其构造的一次谐波失谐的振幅放大因子概率密度函数与随机失谐的形状几乎相同,也就是说在该激励下硬涂层构造出来的刚度和质量的主动失谐并不能降低结构对失谐的敏感性。 上述结果表明:当硬涂层不含阻尼时基于其构造一次谐波主动失谐可以降低叶盘在随机失谐下的响应水平,但能否降低对失谐的敏感性还与激励的形式有关;当硬涂层含阻尼时基于其构建的主动失谐具有主动失谐减振(刚度与质量的主动失谐)和阻尼减振的双重减振性能;扇区间的阻尼失谐会使叶盘对失谐的敏感性增加。 事实上,上述结果仅基于一次谐波主动失谐模式,为了进一步减小基于硬涂层主动失谐叶盘的振动,在选择硬涂层涂敷方案时(即各扇区叶片的涂敷规律时),应综合考虑阻尼失谐的影响。 本文通过对各扇区叶片涂敷不同厚度的硬涂层阻尼来构造主动失谐,从SNM方法出发同时根据泰勒展开和最小二乘法建立了主动失谐叶盘的有限元减缩模型,并对比了减缩模型与完整有限元模型的计算结果。接着利用建立的减缩模型与蒙特卡罗模拟分析了行波激励下的硬涂层构造的主动失谐叶盘的响应特性,得到以下结论: (1) 通过对比完整有限元模型与减缩模型计算的叶尖响应对比得出:该减缩模型具有较高的计算精度,并且可以有效避免涂层厚度(主动失谐的设计参数)变化时的有限元模型重建。 (2) 通过计算硬涂层含材料阻尼与不含材料阻尼时基于其构建的主动失谐叶盘以及随机失谐叶盘的响应特性得到:基于硬涂层的主动失谐具有主动失谐减振(刚度与质量的主动失谐)和阻尼减振的双重减振性能,并且减振效果明显;扇区间的阻尼失谐会增加叶盘对失谐的敏感性。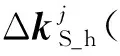
1.2 减缩方程与求解

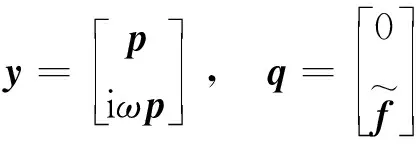
1.3 激励形式
2 主动失谐叶盘振动特性分析
2.1 模型校验

2.2 主动失谐叶盘响应特性


3 结 论

