叶片平均频率对失谐叶盘振动局部化影响分析

张宏远 ，袁惠群 ，孙红运

（1.沈阳理工大学汽车与交通学院，沈阳110159；2.东北大学机械工程与自动化学院，沈阳110819；3.沈阳理工大学科技开发总公司，沈阳110003）

0 引言

失谐振动是航空发动机压气机叶盘系统振动的主要问题，失谐即各叶片之间由刚度、质量等因素导致的固有频率的不同，会进一步导致叶盘系统振动局部化现象[1-2]，从而造成叶盘系统的疲劳破坏[3]。

很多学者对失谐叶盘振动局部化进行了大量研究。于长波等[4]采用有限元模型对失谐叶盘振动概率响应局部化特性进行了研究；王艾伦等[5]采用集中参数模型和蒙特卡罗分析方法，研究了成组叶盘系统的随机失谐特性，分析了失谐敏感性和失谐强度的关系；曾海楠等[6]基于集中参数模型，考虑了榫头榫槽之间的摩擦与间隙，对失谐叶盘进行振动局部化特性研究；刘雅琳等[7]基于微滑移模型研究了干摩擦阻尼对失谐叶盘振动局部化的影响；董明晶等[8]基于整圈自带冠叶盘模型，研究了冠间间隙失谐情况下的叶盘振动局部化特性；高阳等[9]以集中参数模型研究了失谐强度对模态局部化的影响；Kan X等[10]在失谐叶盘振动局部化分析中考虑了科氏力效应的作用；Castanier等[11-12]从激励阶次角度研究了失谐叶盘振动响应特性，对叶盘系统进行动力学分析；针对谐调叶盘系统可以采用循环对称建模技术[13-14]；针对失谐叶盘系统一般采用子结构缩减建模技术[15-17]。但叶片平均频率对失谐叶盘振动响应及振动局部化特性影响方面的研究未见相关文献报道。

为此，本文对航空发动机压气机失谐叶盘振动响应进行分析，对不同叶片平均频率和失谐标准差对失谐叶盘振动特性影响作了探讨，并分析了对振动局部化特性的影响，为失谐叶盘振动特性分析提供了1种新方法，并为控制失谐叶盘振动幅值和降低振动局部化程度提供了有效手段。

1 叶盘系统动力学模型

由于失谐破坏了叶盘结构的圆周循环对称性，不能采用循环对称模型进行动力学分析，又由于整体叶盘模型划分的单元节点数量巨大导致计算困难，因此基于子结构模态综合法，采用有限元缩减模型进行失谐叶盘动力学分析，每个叶片及与其相连接的轮盘部分划分为子结构，按照叶片数将叶盘模型划分为38个子结构，叶片和轮盘网格划分分别采用solid45单元和solid187单元，每个子结构有限元模型由52163个单元和79174个节点构成。叶盘系统材料属性见表1，叶盘有限元模型如图1所示。

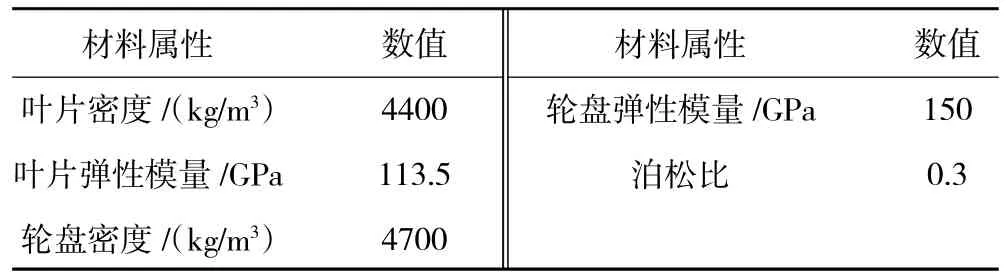
表1 叶盘系统材料属性

图1 叶盘有限元模型

叶盘子结构的振动方程为

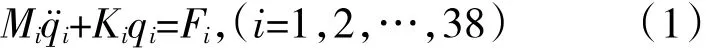
式中：Mi、Ki、qi、Fi分别为第 i个子结构的质量、刚度、位移和作用力矩阵。

采用文献[17]中的子结构减缩建模方法可获得叶盘系统自由度缩减后的强迫振动方程

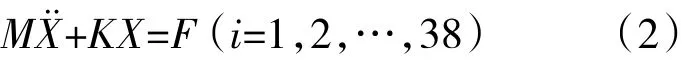
式中：X为广义坐标下的位移。

2 叶盘振动响应特性

当叶盘系统失谐时，式（2）可以表示为

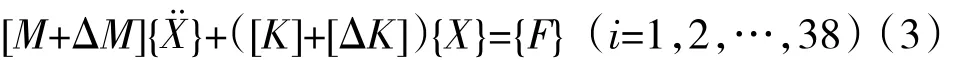
式中：ΔM为质量失谐矩阵；[ΔK]为刚度失谐矩阵；{F}为激振力矩阵，激振力载荷的实部值和虚部值由下列公式[12]确定

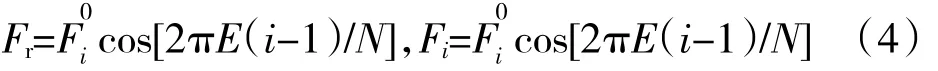
式中：E为激励阶次；N为转子叶片数。

叶片频率失谐对于叶盘系统的振动局部化影响显著，为了便于分析，文中对激励频率、振幅、应变能和平均频率等都做了无量纲化。为了探究不同叶片平均频率对失谐叶盘系统的影响，以弹性模量113、113.5、114和114.5 GPa分别与113.5 GPa的比值作为平均频率，即无量刚化平均频率分别为0.9956、1.0000、1.0044、1.0088。通过获得的4组叶片无量纲平均频率分别进行谐调和失谐叶盘强迫振动响应分析。

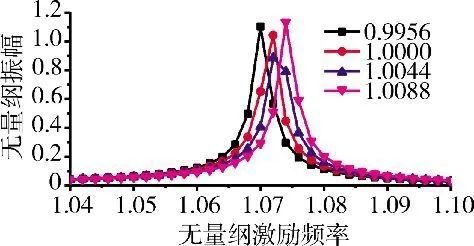
图2 不同平均频率下谐调叶盘系统幅频特性

2.1 谐调叶盘振动响应特性

当不考虑失谐影响时，即谐调叶盘情况下，设置所有叶片的弹性模量一致，求得在4组平均频率下叶盘系统振动响应特性的幅频特性，如图2所示。

从图中可见，当叶盘系统不考虑失谐，即谐调叶盘在不同平均频率下，叶盘系统发生共振的峰值只有1个，且无量纲振幅较小。当平均频率为1.0088、无量纲激励频率为1.074时，叶盘系统无量纲振幅最大，最大振幅为1.133；随着平均频率的增大，叶盘系统的刚度增大，发生共振的频率也逐渐增大。

2.2 失谐叶盘振动响应特性

对式（3）中的[ΔK]按照弹性模量失谐模式进行识别，当失谐标准差分别为1%、5%、8%时，分析平均频率对失谐叶盘系统幅值的影响，失谐标准差为1%时不同平均频率下叶片的失谐量如图3所示。

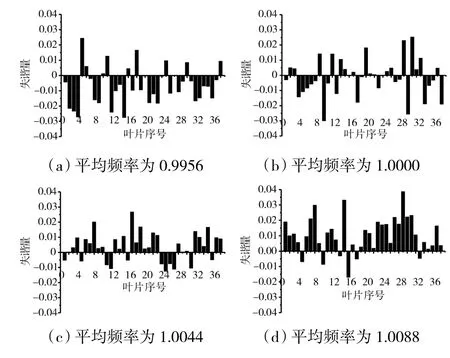
图3 失谐标准差为1%时各叶片失谐量

按照正态分布，选取失谐标准差为1%，对不同平均频率下叶盘系统进行振动响应分析，如图4所示。从图中可见，当平均频率为0.9956、无量纲激励频率为1.070时，叶盘系统发生共振，只有1个峰值，最大振幅为1.85。当平均频率为1.0044、无量纲激励频率为1.072时，叶盘系统发生共振的最大振幅为1.48667。随着平均频率的增大，叶盘系统的振幅在平均频率为0.9956时达到最大，在平均频率为1.0044时最大幅值最小。对比图2、4可见，失谐导致了叶盘系统振动幅值增大。

选取失谐标准差为1%，对不同平均频率下叶盘系统进行应变能分析，如图5所示。从图中可见，随着平均频率的增大，当平均频率为0.9956时，叶片12、14的应变能较大，分别为 2.67、3.25，局部化程度较高；当平均频率为1.0000、1.0088 时，叶片应变能大幅度降低；当平均频率为1.0088时，叶片最大无量纲应变能值最小，小于2.0。

图4 标准差为1%时不同平均频率下叶盘系统幅频特性

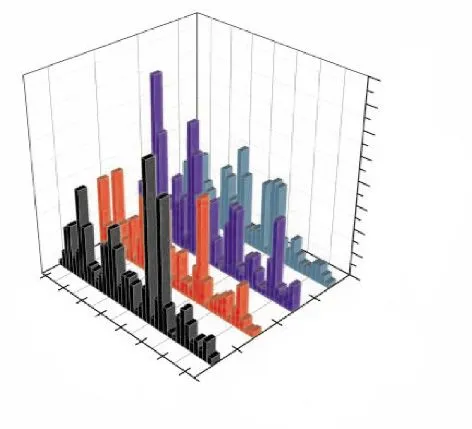
图5 失谐叶盘系统标准差为1%时叶片应变能随不同平均频率的分布

选取失谐标准差为5%，对不同平均频率下叶盘系统进行振动响应分析，如图6所示。从图中可见，当失谐标准差增大到5%时，叶盘系统的共振带变宽，带宽达到0.08，共振幅值大幅度降低，只有当平均频率为1.0088时，幅值大于1.6。

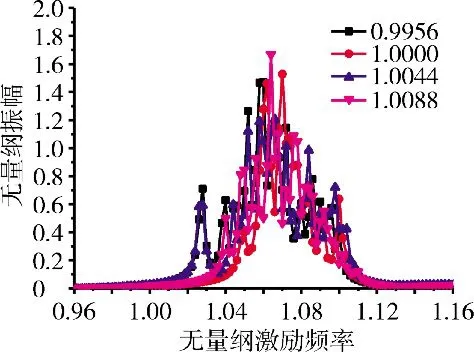
图6 标准差为5%时不同平均频率下叶盘系统幅频特性

选取失谐标准差为5%，对不同平均频率下叶盘系统进行应变能分析，如图7所示。从图中可见，在平均频率为0.9956时，25号叶片应变能达到最大，为4.09；随着平均频率的增大，叶片应变能大幅度降低，在平均频率为1.0044时，叶片最大应变能值最小，只有2个叶片的应变能大于1.5，没有局部化现象，其他3个平均频率都有局部化现象出现。

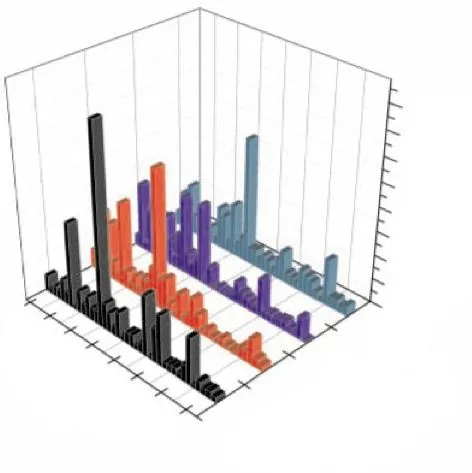
图7 失谐叶盘系统标准差为5%时叶片应变能随不同平均频率的分布

选取失谐标准差为8%，对不同平均频率下叶盘系统进行振动响应分析，得到不同平均频率下叶盘系统振动幅值分布，如图8所示。从图中可见，当失谐标准差增大到8%时，叶盘系统的共振带变宽，带宽达到0.1，共振幅值大幅度减小，只有当平均频率为0.9956时，幅值大于1.6。失谐叶盘系统在标准差为8%时，叶片应变能随不同平均频率的分布如图9所示。从图中可见，在失谐标准差为8%时，除了平均频率为1.0时个别应变能较小，其他几个平均频率下应变能均较大，局部化程度较高。

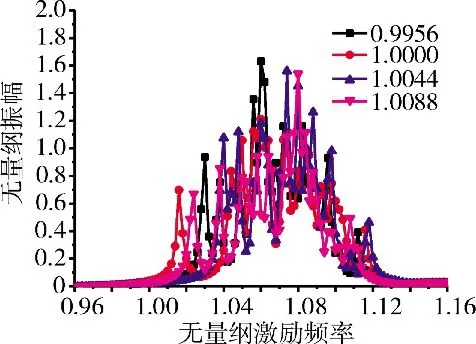
图8 标准差为8%时不同平均频率下叶盘系统幅频特性

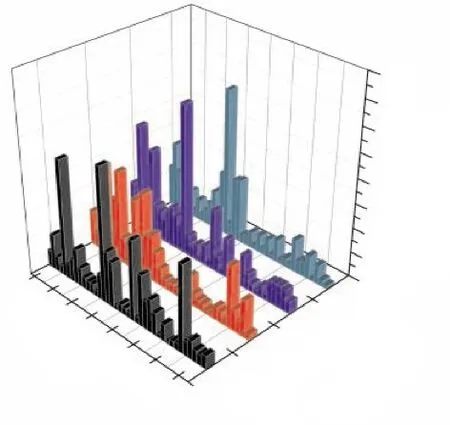
图9 失谐叶盘系统标准差为8%时叶片应变能随不同平均频率的分布

3 失谐叶盘振动局部化特性

为了探究不同平均频率和失谐标准差对失谐叶盘振动局部化特性影响，分别选取失谐标准差为1%、5%、8%，对不同平均频率下失谐叶盘振动特性进行分析。不同失谐标准差条件下各叶片最大应变能分布如图10所示。从图中可见，随着平均频率的提高，大部分叶片应变能大幅度降低；总体趋势上来看，随着失谐标准差的增大，大部分叶片的应变能也呈降低趋势，但是随着失谐标准差的增大，应变能集中在少数叶片上，局部化现象较严重。

为了评价叶盘失谐振动的局部化程度，采用相对振动局部化因子L[12]

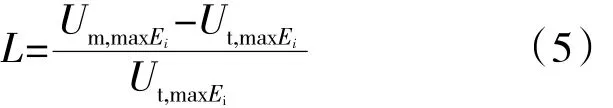
式中：Um,maxEi、Ut,maxEi分别为激励阶次为i时失谐叶盘和谐调叶盘的应变能最大值。

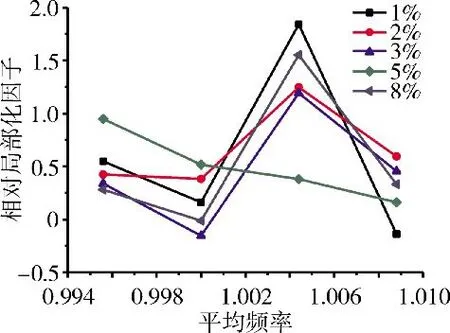
图11 不同平均频率的失谐叶盘系统应变能局部化因子

在不同平均频率下失谐叶盘系统应变能局部化情况如图11所示。从图中可见，在不同失谐标准差下，叶盘系统应变能相对局部化因子变化趋势大体相同，在平均频率为1.0044时出现了严重的局部化现象，由于在平均频率下失谐叶盘应变能较大，但谐调叶盘应变能较小，相对局部化因子计算采用失谐和谐调差值再比值的计算方法，谐调叶盘应变能的大小对于局部化程度影响较大，导致相对局部化因子较大；在失谐标准差为5%时，叶盘系统应变能相对局部化因子变化较小，相对比较平坦，由此可以说明在失谐标准差为5%时，叶盘系统的应变能分布较好。

4 结论

基于子结构有限元缩减模型，开展了叶片平均频率对失谐叶盘振动局部化特性影响研究，得出如下结论：

（1）通过对叶片失谐参数选取不同失谐标准差进行振动响应分析，获得了失谐叶盘振动幅值随失谐标准差的变化规律：随着失谐标准差的增大，叶盘系统最大振幅呈现减小的趋势，且共振带变宽。

（2）通过在不同失谐标准差和不同平均频率下对失谐叶盘系统进行振动响应分析，以及相对局部化因子计算，获得失谐叶盘振动局部化分布情况：失谐叶盘系统在平均频率为1.0044时出现了严重的局部化现象；当失谐标准差为5%时，叶盘系统的振动局部化程度较轻。