基于分裂激盘的进气道/风扇联合流场计算

张博涵，王 强，谢业平

（1.北京航空航天大学能源与动力工程学院，北京100083；2.中国航发沈阳发动机研究所，沈阳110015）

0 引言

发动机和进气道是飞机推进系统的2大主要部件，发动机要吸入空气，为飞机提供不同飞行状态所需的动力，而进气道则需要保证在不同飞行条件下流入发动机的空气流量和空气品质等，从而保证发动机正常工作。因此，进气道与发动机之间需要有良好的适应性关系，否则将对发动机乃至整个推进系统的稳定性和综合性能产生严重影响[1]。

现代战斗机机身和推进系统的整合涵盖了从飞机稳定性到控制，再到进气道/发动机相容性的多种问题[2]。为此，在试验和数值模拟过程中需要使用大量试验和计算资源，并应用各种分析和辅助计算工具。其中进气道/发动机一体化的试验，尤其是关于进气道与发动机相容性的试验，通常需要在风洞和高空试验设施中进行，试验周期长，在前期准备和试验过程中耗资巨大[3]。相比而言，利用数值模拟方法可以在试验前对进气道和发动机的相容性进行预先研究，且可以在一定程度上对试验无法模拟的飞行条件进行计算分析。因此，针对试验出现的问题，可以转而寻找准确、高效的数值模拟方法，来研究进气道和发动机的匹配问题。

对于发动机单独的数值模拟已经有较为成熟的计算方法，也发展了一系列快速而精确的计算程序。但由于压气机与进气道气流流动的尺度相差较大，当采用精确的计算方法进行联合计算时，耗时长、效率低、占用的计算资源巨大。由此发展了对压气机部分进行模化的方法，现阶段对风扇的模化方法主要采用激盘模型（Actuator Disk，AD）和彻体力模型，且经过了多年的发展，2种模型已经可以满足进气道和发动机匹配计算的精度要求。激盘模型主要是将风扇的叶片模化成1个无厚度的盘面，原本受风扇作用的气流在盘面上完成叶片对气流的作用，此时在激盘上下游都为正常的进气道内流，使压气机与进气道的尺度相近，提高计算效率[4-6]。而彻体力模型由于在模化时将风扇部分的控制方程变为无黏条件，因此进气道与模化后的风扇只能通过进气道出口的参数相互传递边界条件，而无法进行联合数值计算[7-9]。

在Joo W G[10]建立激盘模型过程中由于忽略了叶栅的厚度，即忽略了叶栅内存储质量和能量的能力以及叶片的径向力，且激盘轴向的位置选择都会对计算结果产生影响。Joo讨论了激盘模型的解与激盘位置的相关性，同时也研究了对出口气流角的修正问题。本文基于Joo W G的激盘模型建立了1种分裂激盘模型（Divided Actuator Disk，DAD），应用分裂激盘模型对进气畸变条件下的3级轴流压气机性能进行分析。

1 分裂激盘模型的建立

用进气道和转子流场对1个激盘模型进行简单描述，如图1所示。风扇被模化成1个平面激盘，位于某一合适的轴向位置，例如在叶片的后缘或者在弦平面上。原本真实存在的叶栅变为转子上、下游的流场，叶片上下游的流场参数靠强加在激盘两侧的边界条件来耦合，从而代替真实风扇对气流的作用。即假想风扇叶片对气流的作用只存在于模化的平面激盘，激盘的上下游均为正常的进气道内流。

图1 激盘模型

将这样的激盘的上下游联系起来需要激盘的边界条件满足以下5个条件[10]：质量守恒；径向动量守恒；滞止焓守恒；指定的相对出口气流角；指定的熵增。第1、3个条件忽略了叶片排存储质量和能量的能力，第2个条件则忽略了叶片作用在流体上的径向力，第4个条件是将风扇对气流的加功作用通过指定的相对出口气流角确定。

由于常规激盘模型的假设，在使用激盘模型时需要根据具体情况对模型进行修正，因此存在一定的局限性。激盘模型的定义是将整个风扇模化成1个无厚度的平面激盘，风扇对气流的作用无法准确、完全地由激盘模拟，因此需要对激盘模型进行相应的修正。当平面激盘选择在叶栅的不同位置时，激盘的径向长度发生变化，与在叶栅后缘和真实风扇径向距离不一致，造成与真实加功量不一致。最终影响激盘模型计算的精确性。

为此，本文在Joo W G建立的激盘模型基础上，将1个平面激盘分开，分别贴合到叶栅的前后缘，发展了分裂激盘模型，可以有效地消除因径向力假设而产生的误差。

分裂激盘模型的网格边界分别与叶片前、后缘的扫掠形状一致（如图2所示），可避免激盘盘面形状以及位置引起的误差，同时也与真实风扇前后气流的流动情况有一定相关性。根据特定假设，可将叶片前、后缘网格单元面上的参数建立起相关控制方程，参与流场的数值迭代。

假设叶栅内气流流线满足以下条件，且激盘后的网格也是依此关系由激盘前网格自动生成的。

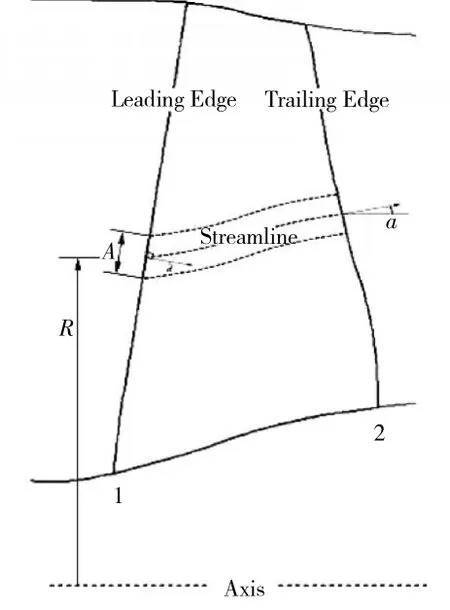
图2 分裂激盘模型总体

式中：R为激盘盘面单元格处流线的半径位置；Rmax、Rmin分别为机匣和轮毂的半径。

这样前、后激盘盘面位置的参数可沿同一条流线建立方程。

由滞止熵守恒条件可得

式中：I为相对坐标系下的滞止熵；ω为风扇角速度；下标1、2分别指叶片前、后缘位置。

由流量守恒条件可得

式中：A为叶片进、出口网格单元面面积；Wˇ为旋转坐标系下A所在网格体的速度向量；dˇ为叶片进、出口网格单元面的法向单位向量，如图3所示。

图3 分裂激盘参数

式中：α为盘面位置流线与轴线的夹角；β为相对坐标系下的叶片出口气流角；dz为dˇ轴向分量；Wz为相对坐标系下速度的轴向分量，与绝对速度轴向分量Vz相同。

相对坐标系下的滞止熵又可表示为

由此得到关于密度ρ的方程为

式中：m为通过网格单元面的单位流量。

由式（7）求解密度，然后得到流场中其他参数的值。

同时由于转动的叶片与气流的相对速度可能会大于声速，这种情况下叶栅会发生喘振，前面描述的分裂激盘模型中不包括叶片的这种流动堵塞作用，因此无法预测叶片通道的堵塞。本文使用1种基于堵塞叶片中2维流动特性的简单模型来确定堵塞流量。2维叶片通道中堵塞流动如图4所示。假设整个叶片通道流动条件是均匀的，则可简单计算出喉道的有效面积。

图4 在叶片通道内的堵塞流动

忽略声速线上游的损失，可得到通过叶片通道的最大质量流量，流量守恒为

式中：A1和A*为激盘入口和喉道横截面积处流管轴向的横截面积；上标rel指相对于叶片；F*为合适的可压流函数。

由于前面假设了叶片通道的流线满足式（1），则该流量守恒公式可直接对流线两侧单元格参数进行控制。

分裂激盘模型的边界条件都通过这个堵塞模型式（8）规定的最大流量进行判断和控制。如果流量比堵塞流量小，那么分裂激盘的进口边界条件由原模型给出；否则进口单元格的流量就固定为堵塞的值，这时通过使用堵塞的流量计算得到出口单元格的流动变量，直接指定出口单元格的流量并继续计算。

2 分裂激盘模型的验证

2.1 研究对象

本文以NASA Rotor 67风扇转子作为研究对象[11]。Rotor 67转子设计用于轴向流动，工作时作为孤立转子，没有进口导叶和静叶。由于叶型数据公开且有详细的试验结果，因此有大量针对该转子的理论和数值研究工作[12-13]。其基本参数见表1，具体的几何参数与试验数据参考文献[14]。

表1 Rotor 67转子基本参数

根据文献[14]中的代码自动生成叶片与流道的几何参数，如图5所示。

2.2 模型验证

图5 Rotor 67和流道的几何模型

由于激盘模型原则上是基于3维数值模拟的简化模拟方法，因此本文中验证部分分裂激盘模型的参数依据A.Arnone的计算结果[15]。通过使用可变系数，采用隐式残差平滑和完全多重网格的方法，提高了4阶Runge-Kutta法的计算效率。使用多重网格方法对NASA Rotor 67转子计算，结果如图6所示。从图中可见，模拟结果与NASA公开的试验结果一致性较好。

根据Arnone方法的计算结果，选取风扇在峰值效率点工作时的出口相对气流角径向分布和绝热效率，建立分裂激盘模型。其中叶片前、后缘和相对出口气流角均使用二次曲线进行拟合，沿轴向截面的网格如图7所示。

图6 NASA rotor 67转子在设计转速时的性能

图7 分裂激盘模型沿流向截面的网格

边界条件设置与3维模拟一致，压力入口总压为101325 Pa，总温为288.15 K，壁面速度无滑移。设置不同出口反压，模拟结果如图8所示。从图中可见，模型计算的压比整体略高于全3维模拟结果，从接近失速到接近堵塞范围内与3维模拟的误差最大约3%，在接近最高效率点的一致性很好。在接近失速以及失速时由于模型的局限性，模型的计算结果与全3维模拟结果偏差较大，这是不可避免的。在风扇正常工作范围内，模型的压比稍大于3维模拟的，究其原因主要是模型采用的绝热效率为3维模拟中的峰值效率，所以模型计算的压比整体偏高[16]。但由于峰值绝热效率是评价风扇性能的重要参数，因此在考虑了模型针对个体的精确性和普适性后，坚持选择风扇的峰值效率作为模型的输入参数。

图8 压比特性对比

在最高效率点的模型方法与3维模拟计算的压比沿相对叶高的分布如图9所示。从图中可见，在叶根和叶尖处模型的结果与3维模拟结果偏差较大，主要是由于激盘模型对边界层流动的处理方法有局限性，且叶尖部分在3维模拟中考虑了转子的叶尖间隙，而在模型计算中没考虑，以上多种原因共同导致压比偏差。

本文模型与Joo W G的激盘模型对Rotor 67转子的压比特性模拟结果对比如图10所示，其中激盘模型的激盘位置位于风扇出口。从图中可见，分裂激盘模型改进了激盘模型的结果。风扇在正常工作范围内，分裂激盘模拟的压比特性更接近于3维模拟结果，主要由于分裂激盘模型的边界基本拟合了风扇进、出口的几何形状，而激盘模型的边界为环形平面，引起相对出口气流角的误差，进一步产生风扇加功量不同的问题。而且分裂激盘模型不需要选择激盘盘面的位置和后续的修正，相对于激盘模型能够更加准确地模拟风扇的特性。

图9 最高效率点下总压比径向分布

图10 分裂激盘模型与激盘模型的压比特性对比

由于在建立分裂激盘模型时，控制方程的时间复杂度并没有成比例增加，监控计算过程的残差如图11所示。从图中可见，2种模型残差的收敛速度量级相当。由于本文模型对3维定常流场的N-S方程采用3阶精度有限体积法离散，隐式LU-SGS（虚）时间推进法迭代求解。对流通量采用Roe格式计算，扩散通量采用中心差分格式计算。湍流模型为CG K-epsilon线性湍流模型，模型参数输运方程采用混合隐式迭代加解析方法求解，因此可以通过K和epsilon的残差量级判断计算是否收敛。图中K与epsilon的残差量最终都在10-4量级以下，可认为计算达到收敛。

图11 Rotor67转子计算残差对比

3 分裂激盘模型对总压畸变的模拟

3.1 压气机模型与畸变条件

本文选用的多级压气机模型为NASA Compressor 74A。该压气机为5级核心压气机，由于文献[17]中研究了前3级的总体性能，因此本文也仅对压气机的前3级进行模拟和分析。压气机基本结构如图12所示，基本设计参数见表2。

图12 NASA Compressor 74A压气机前3级叶型流道结构

表2 压气机前3级基本参数

分别对无畸变和畸变条件下的压气机气动稳定性进行分析，以检测分裂激盘模型对于稳态总压畸变的模拟能力。其中畸变条件的进口总压给定如图13所示。为模拟进气道出口畸变情况，设置为既存在径向畸变又存在周向畸变。无畸变区总压为101325 Pa，低压畸变区总压为无畸变区的90%。

图13 进口总压分布

3.2 畸变模拟结果分析

压气机前3级叶栅进、出口的总压分布如图14所示。从图中可见，进口的总压畸变对叶栅区域的总压分布产生影响，畸变区气流的径向分布引起压气机内气流径向重新分布；叶尖周向总压的分布也显示出经过叶栅后，气流发生掺混；经过前3级叶栅后，总压畸变有一定改善。

图14 压气机前3级进、出口的总压分布

在设计转速下进口总压畸变与无畸变的压气机流量-压升特性曲线对比如图15所示。从图中可见，总压畸变导致压气机总压比减小，且畸变时压气机的特性曲线整体向失速边界靠近，表明该模型能模拟总压畸变对压气机性能的影响。

图15 压气机压比特性对比

4 进气道/风扇联合流场数值计算

由于已经验证了分裂激盘模型可以很好地模拟风扇正常工作时的特性，分别对进气道和风扇的工作特性进行分析，得到共同匹配点后，用分裂激盘模型代替3维风扇模型进行进气道-风扇联合流场的数值模拟研究。

4.1 进气道模型与工作特性

本文所研究的进气道几何形状已经确定，且斜板可根据飞行条件调整角度，如图16所示。第1道斜板前和第2、3道斜板间的角度是固定的，只有第1、2道斜板间可根据来流条件不同与发动机工作状态不同绕接缝转动[18]。

对不同来流马赫数和斜板角度的进气道工作特性进行分析，来流静压均为22700 Pa。选择的典型进气道斜板角度与来流马赫数条件分别为：（1）来流马赫数为1.33，斜板角度为-2.7°；（2）来流马赫数为1.33，斜板角度为 2°；（3）来流马赫数为 2.25，斜板角度为13.14°。得到接近临界状态进气道各项参数见表3。

图16 斜板角度为-2°的进气道几何截面

表3 接近临界状态进气道各项参数

4.2 风扇模型与工作特性

与该变几何进气道匹配的是1.5级风扇，即1排导向叶片、1排动叶和1排静叶。单级风扇定常模拟所用的计算网格如图17所示。在不同转速的计算过程中，导向叶片与轴向的夹角始终为 0°。

图17 1.5级风扇定常计算所用网格

根据图17叶片和风扇流道的几何模型，建立计算域，在进口导叶前和静叶后延伸2个弦的长度作为边界条件的缓冲。使用RANS方法进行数值模拟，由于计算方法已广泛用于风扇3维计算，因此无需对计算结果与计算方法进行验证。得到流场的详细参数与风扇的绝热效率、等熵效率等特性参数。综合各转速下的风扇定常特性，得到风扇压比特性曲线如图18所示。其中设计最大转速为7975 r/min。

图18 风扇总压比特性曲线

4.3 包含分裂激盘的进气道/风扇联合流场模拟

由前2节所得进气道与风扇单独的工作特性，根据换算流量的定义

对于上节的风扇工作特性，由于设置的进口条件与标准大气一致，可以直接将结果作为换算流量和换算转速使用。换算流量匹配如图19所示，其中3条与x轴平行的线分别代表3个进气道换算流量：128.44、110.94、76.87 kg/s。

由此选择斜板角度为2°，Ma=1.33的进气道与设计最大转速为7975 r/min的风扇，理论上流量匹配。应用分裂激盘模型对该状态下的风扇叶栅进行模化，进气道-风扇联合流场的计算域如图20所示，真实的网格划分至动叶的前缘之前，动叶和静叶之间间隙和静叶后的网格均由程序自动生成，如图21所示。

图19 换算流量匹配

图20 联合流场的拓扑结构

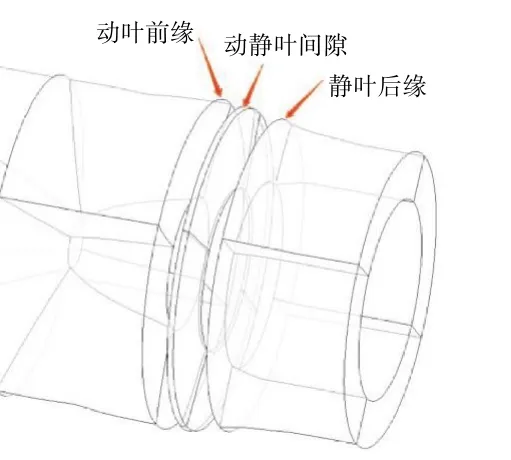
图21 风扇部分自动生成的网格结构

对进气道-压气机联合流场进行数值模拟，可得联合内流特性，如图22所示。从图中可见，联合流场的最大流量要略小于单独进气道的内流最大流量。分析可知主要原因是进气道出口的总压畸变影响了风扇的性能，导致风扇能够通过的最大流量受到限制。

对相同边界条件下的单独进气道与联合流场数值模拟结果对比，内流马赫数与进气道出口的总压分别如图23、24所示。

图22 发动机流量与风扇出口反压的关系

图23 马赫数对比

图24 进气道出口总压对比

由单独进气道与联合流场的结果对比可知，加入分裂激盘模型进行联合计算对进气道内流特性的影响可以忽略。由于理论上已经证明进气道与风扇达到匹配状态，联合流场与单独的数值模拟结果的一致性证明了分裂激盘模型可对进气道/风扇的联合流场进行一体化分析。

5 结论

本文基于激盘模型建立了1个相对更准确的分裂激盘模型，减小了激盘模型假设产生的误差。通过对Rotor 67转子的数值模拟验证，分析多级压气机在稳态总压畸变的性能影响，得到以下结论：

（1）分裂激盘模型对风扇的模化方法使其不需要相应的修正，比常规激盘模型更精确，同时计算收敛速度没有明显减慢。且不同于常规激盘模型激盘前、后流场参数无法使用的问题，该模型由于没有对风扇几何进行模化，因此激盘前、后的流场参数有一定的参考价值。

（2）分别计算进气道和风扇的工作特性，通过折合流量这一参数，得到进气道与风扇流量匹配的理论状态点。通过分裂激盘模型对风扇模化，并与进气道进行联合计算，得到的流场参数验证了使用分裂激盘模型对进发一体化问题的可行性。

综上所述，该模型在原激盘模型的基础上提高了计算精度，更准确地描述了叶栅级之间的流动规律，同时有效地对针对进气道-风扇的联合流场进行性能分析。相对于其他常见的简化模型如黏性彻体力模型，分裂激盘模型可对进气道-压气机流场进行联合数值计算，使其成为分析进发一体化问题的有力工具。