高速铁路轨道-桥梁-土体系统的振动传递特性试验研究

李小珍， 陈桂媛， 朱 艳， 赵 宇

(西南交通大学 桥梁工程系，成都 610031)

当前，我国的高速铁路已取得举世瞩目的成绩。发达的高铁网络在为人们的出行提供便利的同时，也给沿线环境带来了严重的振动污染问题。我国的高铁线路多采用“以桥代路”的模式，因此，研究高架区段从振源到受振体的振动传递特性，对于理解高速列车运行所带来的环境振动问题具有重要意义。

研究高速列车运行引起桥梁、地面振动的方法主要有理论分析、数值模拟和现场测试。在理论分析及数值模拟方面，现有研究通常将整个系统分解成振源、振动传播路径2个部分。例如：陈建国等[1]建立了车-桥和墩-土两个子系统模型，在时域内通过迭代计算得到桥梁支座反力，接着将其作为激励施加于墩-土子系统模型上，并在此基础上讨论了不同因素对地面振动的影响。时瑾等[2]建立了车桥动力分析模型，并结合常用跨度简支箱梁的特点，分析了轨道不平顺、速度和跨度对墩顶动反力时程和频谱的影响规律。

鉴于“车辆-轨道-桥梁-基础-土体”大系统的复杂性，现场测试成为重要的研究手段。张迅等[3]对典型铁路简支箱梁的中高频振动进行了试验研究，并与其它学者的测试结果进行比较分析。李小珍等[4]通过现场锤击试验，对轨道-箱梁的振动传递特性进行了研究。Xia等[5]通过实测北京地铁5号线高架区间的环境振动，比较了不同轨道情况下(梯形轨枕和普通板式轨道)地面振动特性的差异。文献[6-8]实测了不同列车通过不同高架桥时的地面振动，得到了振动衰减规律。Zhai等[9]实测了高速列车以速度300～410 km/h通过路基区段时的地面振动响应。

需要指出的是，以上研究在进行频域分析时，均采用传统的傅里叶变换方法，该方法虽简便可靠，却无法反应信号频谱特性随时间的变化。列车运行引起的振动响应具有明显的非平稳特征。例如，文献[10-11]采用连续小波变换方法对地铁列车运行产生的地面振动实测数据进行了分析，揭示了场地振动的非平稳性特征。Garinei等[12]采用连续小波变换方法分析了减振沟的减振效果，指出连续小波变换方法能够更加全面地反应地面振动信号所携带的信息。Cantero等[13]采用改进的MLP小波基对列车荷载作用下的桥梁结构振动进行分析，发现桥梁振动的频谱特性受车辆编组、行车速度和自振频率的共同影响。

纵观上述车致环境振动试验研究，测试车速大多低于200 km/h，极少数在更高车速下的测试或仅针对路基区段，或没有系统地探究振动传递特性，即振动自轮轨接触处产生，在轨道、桥梁和土体中的传递特性。为此，本文以津秦客专为工程背景，对高速列车运行引起的振动响应进行了监测，列车运行速度为250～385 km/h。结合连续小波变换方法，对轨底、箱梁顶板和底板、墩顶、近场和远场地面土体等不同位置的振动信号进行分析，探讨在经过轨道结构、桥梁结构和土体的多层滤波效应后，振动响应的变化规律。

1 试验设计

1.1 桥梁概况

在津秦客专高架区段上选取双线简支梁作为测试工点。简支梁全长32.6 m，设计速度350 km/h。桥上铺设CRST-II型板式无砟轨道，线间距5 m，采用60 kg/m钢轨和WJ-8C型扣件。桥墩为圆端形实体墩，墩高3 m。承台底设置8根直径1 m的钻孔灌注桩，桩长37 m。场地表层填土厚约1 m，下为砂性地层。

1.2 测点布置

在桥梁跨中截面的钢轨、箱梁顶板和底板上布置垂向加速度传感器，编号为B1～B3(图1)。此外，在墩顶和垂直于线路方向的地面上布置垂向加速度传感器，编号为B4、G1～G8(图1)。

图1 测点布置图(m)

在桥上及墩顶测点安装LC0108型压电加速度传感器(量程0～10g，频响范围0.35～4 000 Hz)，采样频率为10 kHz。在地面测点安装891-II 型加速度传感器(量程0～4g，频响范围0.5～80 Hz)，采样频率为1 024 Hz。数据采集设备采用INV 3060S型24位网络分布式同步采集仪，配合DASP-V10系统对数据进行分析。

测试中运行的高速列车为CRH380A型，8节编组。图2给出了试验列车的特征长度，L1～L4分别代表轴距、前后车相邻转向架的中心距、定距和车长。列车运行在近轨，车速范围为250～385 km/h，各个速度级均获得至少3组有效测试数据。

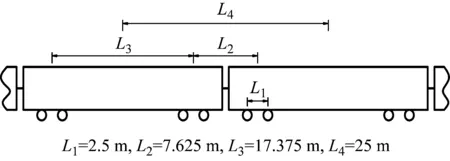
L1=2.5 m,L2=7.625 m,L3=17.375 m,L4=25 m

1.3 振源的频率特性

将列车加载频率记为fi=v/(3.6Li)(i=1,2,3,4)，其中，v为车速，km/h；Li为列车特征长度。相关研究表明，铁路车致地面振动响应的频谱与列车加载频率fi相关。

Zhai等的研究表明，在桥上列车运行引起的地面振动响应的FFT谱上，最大振幅出现在轴距激励频率f1附近，同时振幅在车长激励频率f4及其整数倍附近出现峰值。此外，定距激励频率f3及前后车相邻转向架中心距激励频率f2对振动响应幅值谱起调制作用，使得振动响应在f=(k+0.5)f3或f=(k+0.5)f2(k=1,2,3,…)处振幅为零。

轮轨不平顺激励下，作用在桥梁上的轮轨力具有不同的频谱成分。一般情况下，轮轨力在中频范围具有一个明显的峰值区域，这与轮对簧下质量在弹性支承轨道上的振动有关(对应于车轮-轨道系统固有频率)。文献[14]通过一系列简化处理，得到了该轮轨力峰值频率fp的数学表达式，即

(1)

式中，EI为钢轨的抗弯刚度；S为钢轨每延米的支承刚度(假定钢轨为连续弹性支承)；kH为线性化的轮轨赫兹接触弹簧刚度；mw为单轮质量。采用式(1)求得本试验中，轮轨力的峰值频率约为50 Hz。

2 时频分析

2.1 连续小波变换

设信号x(t)和母小波ψ(t)为平方可积的实数函数，且ψ(t)的傅里叶变换满足容许性条件。将ψ(t)进行伸缩和平移后得到小波基，记为

(2)

式中：a为尺度因子，a>0；b为平移因子。

信号x(t)的小波变换表达式为[15]

(3)

式中：上标“*”代表取共轭；Wx(a,b)称为小波系数。

该研究结果表明：MLP小波基具有优异的时间、频率分辨率。因此，本文采用MLP小波基进行小波变换，其表达式如下

(4)

2.2 轨道、桥梁振动

现以车速350 km/h下的某一有效测试样本为例，对轨道、桥梁的振动进行分析。

图3给出了钢轨垂向振动加速度(B1)的时程和傅里叶变换幅值谱。从时程曲线上可观测到9处峰值，对应于轮轴荷载。从幅值谱上可以看出钢轨振动表现出宽频特性，振动能量在2 000～2 500 Hz附近出现明显峰值，峰值加速度约为23.7 m/s2。进一步观察幅值谱可发现，钢轨振动频谱中的局部小峰值为3.9 Hz的倍数，即对应于车长激励频率f4。

(a) 时程

(b) 幅值谱

研究表明，经过扣件、轨道板和底座板等部件的滤波效应后，振动能量在从钢轨传递至箱梁的过程中迅速衰减，不再呈现宽频特性，且主要集中在200 Hz以内。为此，这里采用连续小波变换对桥梁振动信号进行分析，结果如图4所示。

从图4可以看出，箱梁顶板(B2)、底板(B3)及墩顶(B4)的振动响应均表现出明显的冲击振动特性，冲击次数与列车轮轴对应。顶板的振动能量分布在30～200 Hz，峰值频率出现在39 Hz附近。底板的振动能量分布稍集中，峰值频率出现在50 Hz。相比之下，墩顶的振动能量在频率分布上更宽，在30～240 Hz的频率范围内均有分布。

2.3 地面振动

垂直于线路方向上地面的振动响应如图5所示。可以看出：地面各测点的振动响应同样表现出非平稳特性，信号能量不仅具有局部频带集中特性，在时域上亦存在局部集中特点，对应于列车轮轴的冲击荷载；在距离桥墩40 m范围内，可清晰地观测到地面振动响应的峰值频率及轮轴的周期性加载现象。

另一方面，进一步观察图5可以看出，车速为350 km/h时，地面测点振动响应的峰值频率出现在39 Hz或50 Hz附近(图中已圈出明显的峰值频率)，分别对应于轮轴加载频率及轮轨力的峰值频率。

为了说明地面振动峰值频率与车速的关系，表1罗列了不同车速下地面各测点的振动峰值频率。不难发现，地面振动的频谱特性主要由轮轴激励频率f1和轮轨力峰值频率fp共同决定。

(a) 顶板(B2)

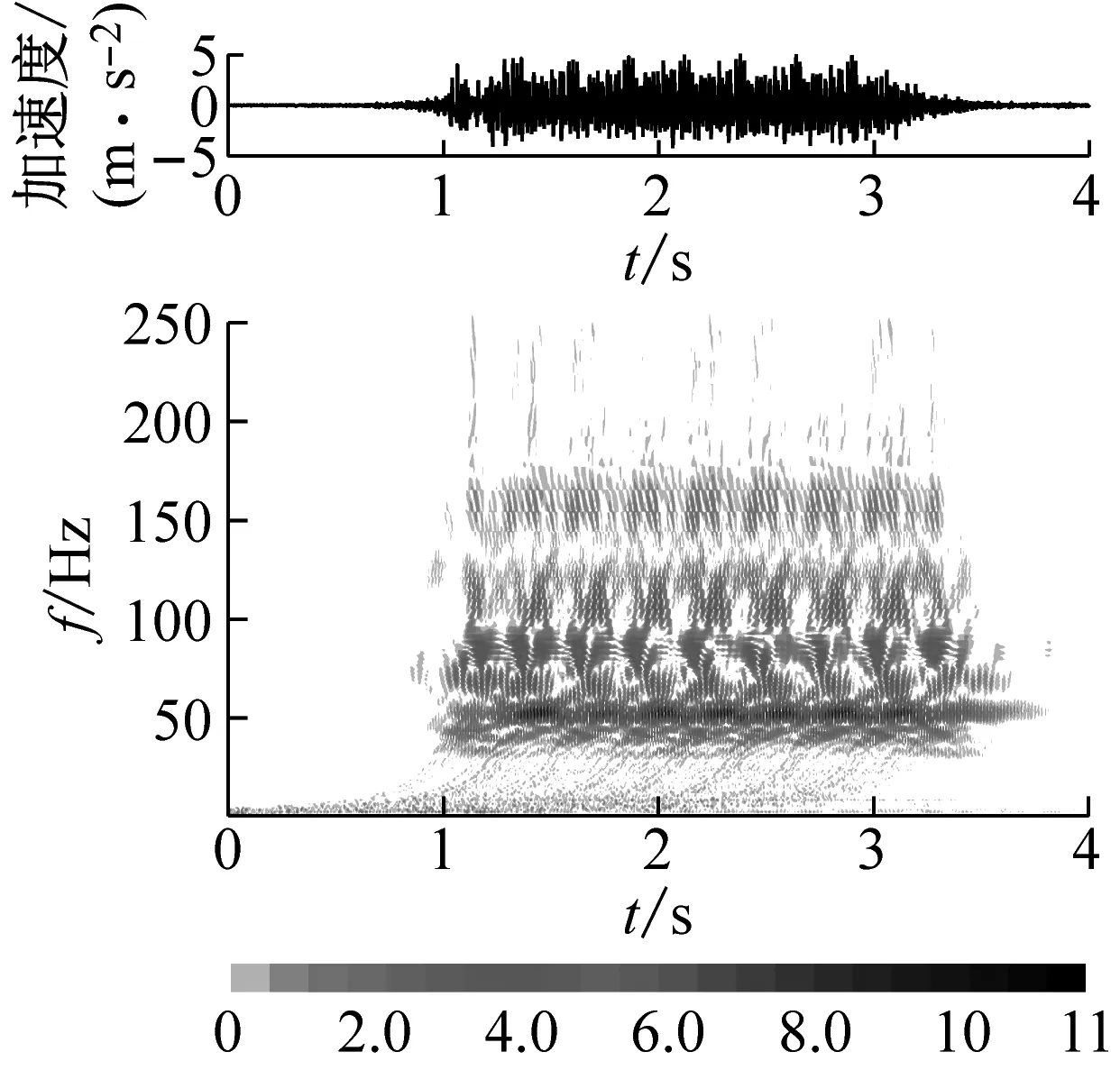
(b) 底板(B3)

(c) 墩顶(B4)

图4 桥梁垂向振动时频分布

Fig.4 Time-history distributions of the bridge vertical vibrations

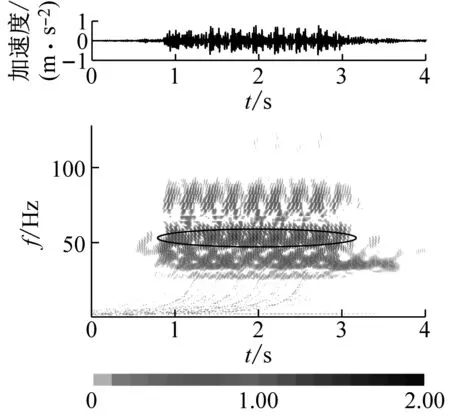
(a) 墩旁(G1)

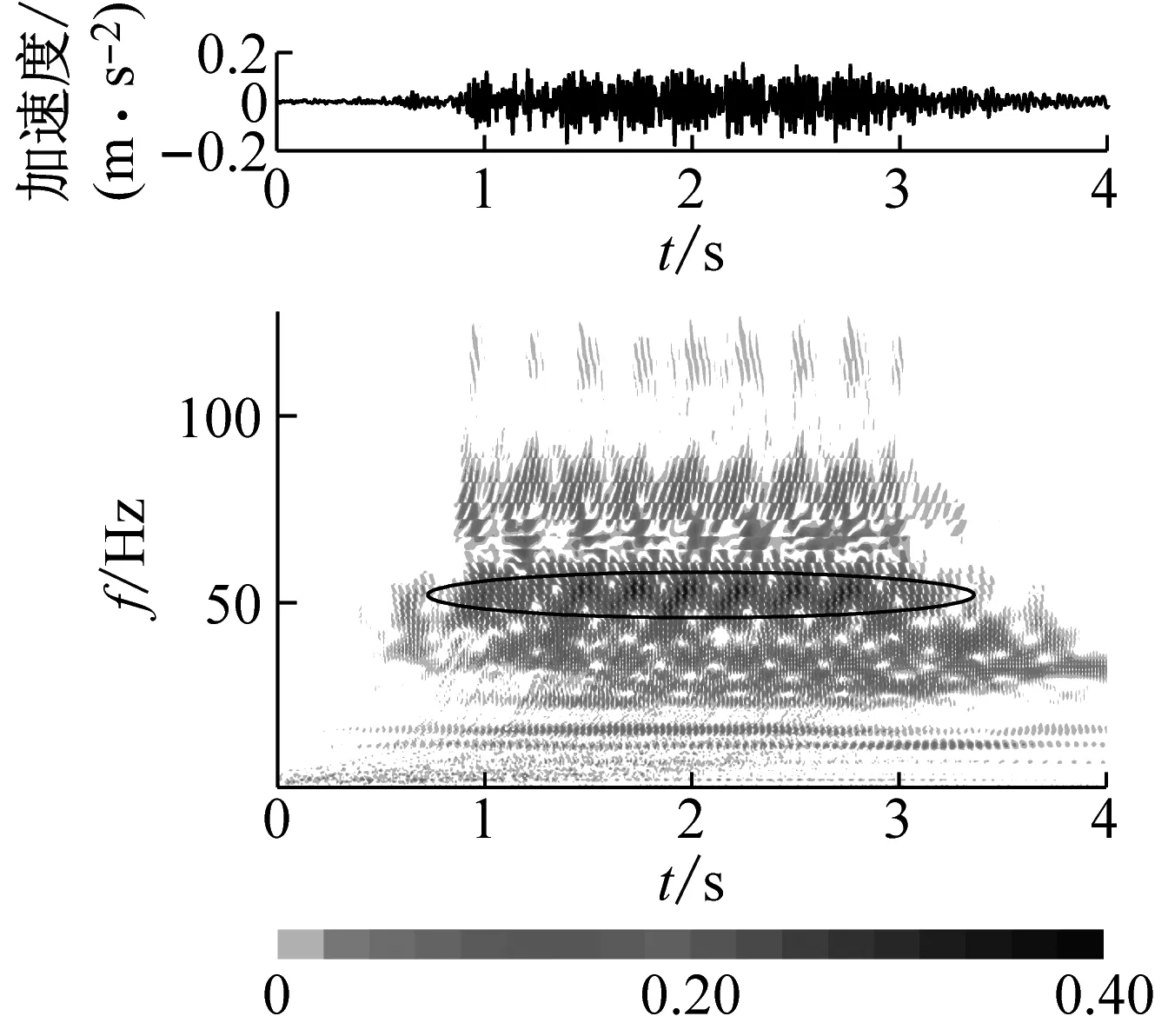
(b) 7.5 m处(G2)

(d) 22.5 m处(G4)

(e) 30 m处(G5)

(f) 40 m处(G6)

图5 地面垂向振动的时频分布

Fig.5 Time-history distributions of the ground vibration

表1 不同车速下的地面振动峰值频率

2.4 小波能量累积曲线

对桥梁和地面振动信号的连续小波变换结果进一步处理，做出小波能量随时间的累积曲线，结果如图6所示。可见，各条曲线均存在8段明显的“阶梯”跳跃(图中以虚线分割)，对应于时频分布图中的时域、频域局部集中特性。

表2给出了小波能量累积曲线中每一个“阶梯”跳跃对应的能量增加量占总能量的百分比。由表中数据可以看出，除最后一个台阶外，其它各台阶内的能量增

加量相近。因此，针对桥梁和地面测点，振动响应的影响范围约为本节车和后一节车(即相邻两节车)。

(a) 桥梁

(b) 地表

Tab.2 Percentage of wavelet energy increments %

3 振动传递特性

3.1 1/3倍频程谱

采用1/3倍频程分频振级分析方法，进一步对各测点的振动响应进行定量分析。采用不计权的方式，计算得到各测点的垂向振动加速度级(记为“VAL”)，参考加速度为10-6m/s2，结果如图7所示。

从图7(a)可以看出：

(1) 钢轨的分频振级明显高于桥梁，前者的最大振级约为160 dB。

(a) 轨道、桥梁

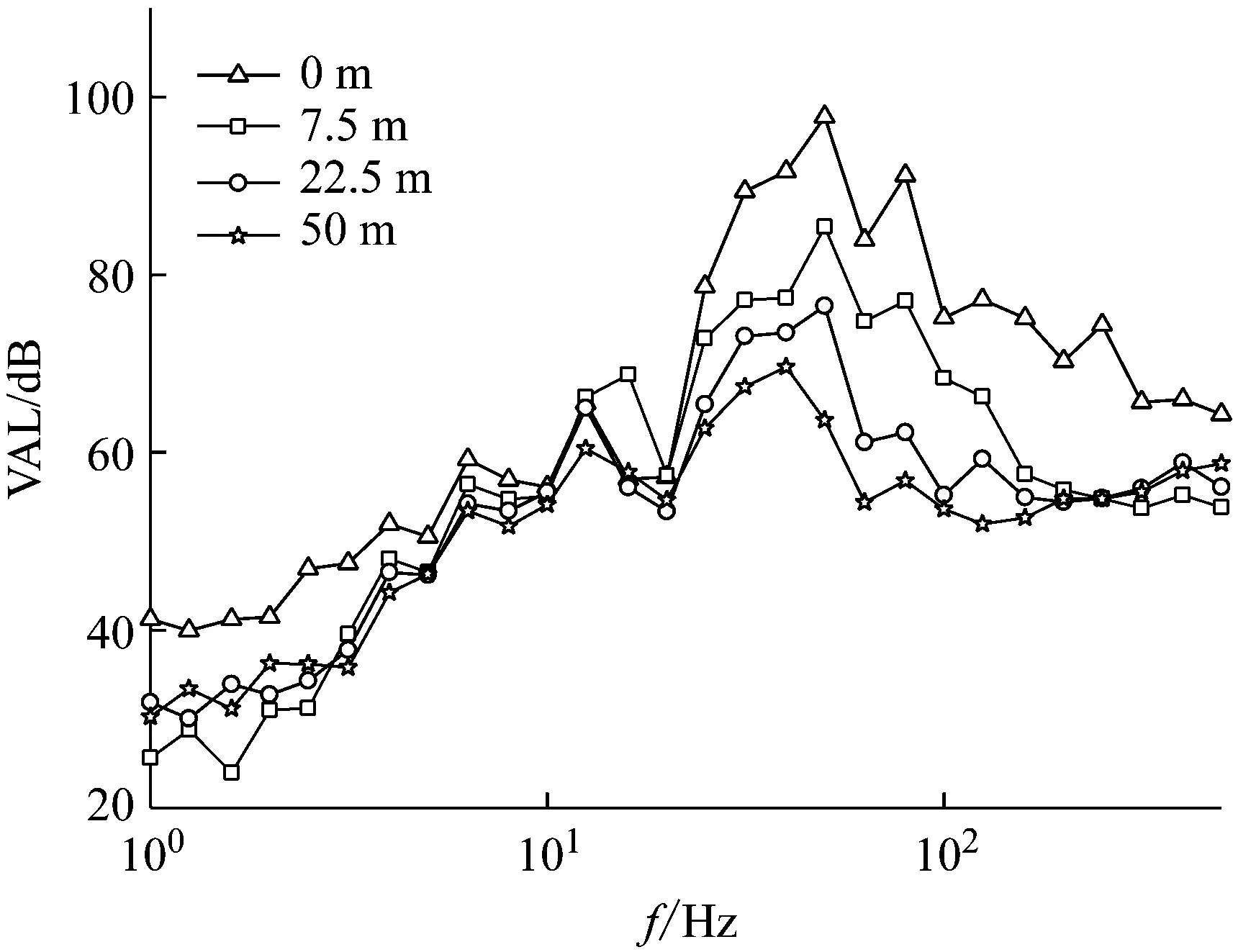
(b) 地面

(2) 从钢轨到箱梁顶板，分频振级在20 Hz以下和200 Hz以上迅速衰减，幅度约为40～60 dB；在20～200 Hz，衰减幅度约为20 dB。

(3) 箱梁顶板的分频振级集中在31.5～125 Hz，最大振级为113 dB，峰值频率为40 Hz。底板的分频振级与顶板接近，但峰值频率为50 Hz。

(4) 由箱梁至墩顶，振级衰减了20～40 dB。墩顶振动能量的优势频段为31.5～125 Hz，且分频振级在该频段内处于70 dB上下。

从图7(b)可以看出：

(1) 由墩顶传递至墩旁的过程中，振动频谱特性发生了很大变化，且振级在31.5～100 Hz频率范围内增加了10～20 dB。

(2) 不同地面位置处的振动响应均在40～50 Hz附近出现峰值。从墩旁至距离桥墩7.5 m处，振动能量显著衰减，其中，在10 Hz以下衰减了8～10 dB，在31.5 Hz以上衰减了近20 dB，即高频振动的衰减幅度明显大于低频振动。

(3) 从7.5 m处至22.5 m、50 m处，振动能量继续衰减，而衰减速率逐渐放缓，但仍可观察到高频振动的衰减速率高于低频振动。另外，不同测点处的地面振动在4～10 Hz频率范围内非常接近。

按照ISO 2631/1—1997国际标准规定的全身铅垂向振动不同频率计权因子计算得到地面振动Z计权振动加速度级(记为“VLz”)，如图8所示。

图8 地面Z计权振级

对比图7(b)及图8可以发现：总体上，Z计权振级小于不计权振级，但对于1～20 Hz的低频部分，Z计权振级与不计权振级十分接近；而当频率高于20 Hz时，Z计权振级迅速衰减。

3.2 车速的影响

本节讨论车速对桥梁和地面振动响应的影响，进一步分析总体振动加速度级(分频振级进行叠加)的变化，结果如图9所示(不计权结果)。

从图9可以看出：

(1) 总体上，各测点的总振级均随车速的增加而增大，但变化率稍有差异。

(2) 箱梁顶板和底板的总振级相近，在116～120 dB之间变化，随车速的变化率为0.33 dB/(10 km/h)。

(3) 相比之下，墩顶的总振级对车速更为敏感，即在82～90 dB之间变化，变化率为0.52 dB/(10 km/h)。

(a) 顶板(B2)

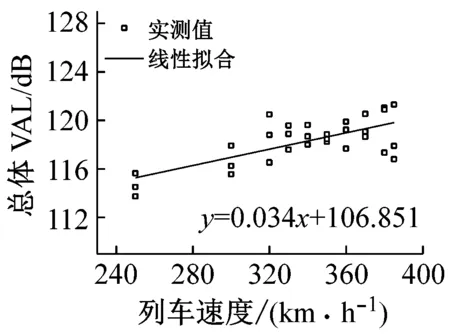
(b) 底板(B3)

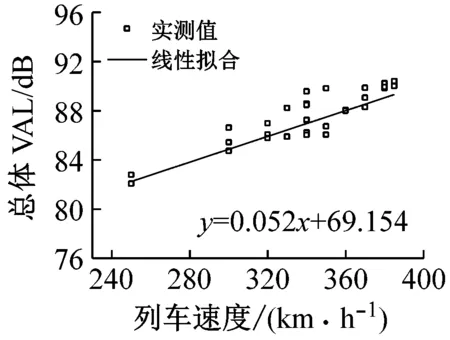
(c) 墩顶(B4)

(d) 墩旁(G1)

(e) 7.5 m处(G2)

(f) 15 m处(G3)

(g) 22.5 m处(G4)

(h) 30 m处(G5)

图9 各测点总体振动加速度级随车速的变化

Fig.9 Variations of overall acceleration levels of all measuring points with train speeds

(4) 墩旁地面的总振级在97～103 dB之间变化，较墩顶增加约15 dB。地面各测点的总振级对车速的敏感程度相近，变化率约为0.22 dB/(10 km/h)，即相比桥梁而言变化率很小。

3.3 地面振动传播规律

选取320～385 km/h速度下的地面振动测试样本，做出不同速度下的总振级散点图及多项式拟合曲线，分别包含不计权和Z计权的结果。

分析图10，得到如下结论：

(1) 不计权和Z计权的总振级随距离的衰减规律均服从3次多项式，但前者要比后者大约10 dB。在不同车速下，地面振动均符合这一规律。

(2) 在近桥墩处，振动随距离增加而迅速衰减；在距桥墩20～40 m范围内，振动随距离的衰减速放缓；在距桥墩40～60 m范围内，衰减率再次增大。

(3) 距离桥墩15 m之外的地面总体Z计权振级均小于80 dB，符合我国GB 10070—88《城市区域环境振动标准》中“铁路干线两侧”区域的垂向振动总体Z振级不得超过80 dB的规定[16]。

4 结 论

本文实测了高速列车以车速250～385 km/h通过32 m简支梁高架区段时的轨道、桥梁和地面振动，通过对实测数据进行分析，得到如下主要结论：

(a) 不计权

Fig.10 Variations of overall vibration acceleration levels of ground measuring points with distance under different train speeds

(1) 各测点的振动响应均具有明显的非平稳特征。地面振动的峰值频率主要受列车周期性轮轴激励频率和轮轨力峰值频率的影响。

(2) 高速列车对桥梁、地面振动响应的影响范围主要集中于相邻两节车，故在建模分析时仅需考虑少数几节车的影响。

(3) 钢轨振动表现出宽频特性，箱梁顶板和底板振动特性相近，墩顶在优势频段内的振动能量趋于均匀分布。地面测点与墩顶测点的振动频谱特性相差很大。地面测点的频谱特性相近，振幅随距离衰减，高频振动衰减更快。

(4) 桥梁、地面的振动响应均随车速增加而增长。箱梁、墩顶和地面的总振级随车速的变化率分别为0.33、0.52和0.22 dB/(10 km/h)。

(5) 在距桥墩60 m范围内，地面振动随距离的衰减规律服从3次多项式。车速为320～385 km/h时，距离桥墩15 m之外的地面总体Z计权振级小于80 dB。