常用刀具后刀面的形成分析
焦余华,彭礼颖
江苏爵克数控刀具有限公司
1 引言
切削刀具必须与现代高效的数控机床相匹配,国内外刀具工作者对刀具结构进行了创新研究,巧妙地改进刀具结构使其达到高效、高精度、高耐用度的要求。刀具后刀面的结构至关重要,对刀具刚性、排屑、结构是否美观和使用是否方便有较大影响。
常用刀具后刀面的形状很多,可分为直平面后刀面、圆弧型后刀面、圆锥面后刀面和曲线型面后刀面;按刀具后刀面是否产生后角可分为不带后角和带后角的后刀面;按后刀面形成的空间可分为二维空间的后刀面和三维空间的后刀面;按刀具形成的后刀面数量可分为一次后刀面、二次后刀面以及多次后刀面。其中,多次后刀面可由直平面、圆弧面、圆锥面、椭圆面、螺旋面或其他曲面组成任意组合的复合后刀面。本文简述了几种典型刀具一次后刀面的形成。
2 直平面后刀面
常见的直平面后刀面刀具有车刀后刀面(见图1)、直平面后刀面的盘铣刀(见图2)、立铣刀端齿后刀面(见图3)、数控刀片(见图4)以及铰刀切削锥后刀面(见图5)等。
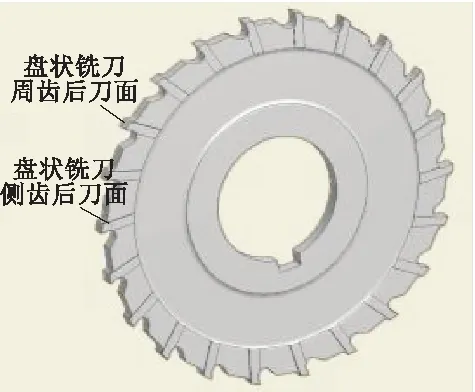
图2 盘状铣刀后刀面

图3 立铣刀后刀面

图4 数控刀片后刀面
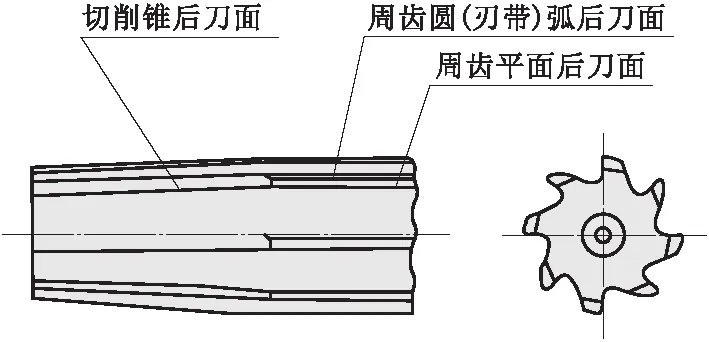
图5 铰刀后刀面
2.1 杆状刀具直平面后刀面的形成
杆状刀具直平面后刀面的形成方法一般是在工具磨床上用碗形砂轮的平端面刃磨杆状刀齿后刀面。现以直柄铰刀刀齿后刀面的手动加工方法为例说明形成的原理。
①选好砂轮并装在工具磨磨头上,将碗形砂轮的平端修整成内凹形的锥面。
②将铰刀安装在二顶尖间。
③根据确定的砂轮退刀方向,将磨头转过1°~2°(见图6),以便砂轮退刀,保证砂轮只有一个边缘参与磨削。
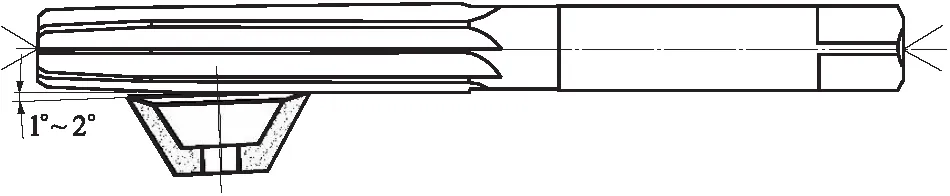
图6 直柄铰刀磨刀齿后刀面磨头偏转
④利用中心规调整支片高度(见图7),支片高度比铰刀中心的高度低H,公式为

图7 磨直柄铰刀刀齿后刀面支片与铰刀中心相对位置
(1)
式中,d为铰刀直径;α为刀齿后角。
⑤启动砂轮,砂轮顺转磨削,砂轮的旋转使铰刀前刀面紧贴支片,开始刃磨。手扶铰刀,使刀齿前刀面紧贴支片顶端,另一只手推动工作台作纵向进给。逐齿刃磨,磨完一圈后作一次横向进给,继续刃磨。
2.2 盘状刀具直平面后刀面的形成
典型的盘状刀具直平面后刀面的产品如三面刃铣刀(见图8)。平面后刀面可用铣削、刨削或工具磨床制造,工具磨床有数控工具磨床和万能工具磨床。形成盘状刀具平面后刀面的原理是在盘状刀具内孔中加一定位芯杆,其余与杆状刀具直平面后刀面的形成方法相似。
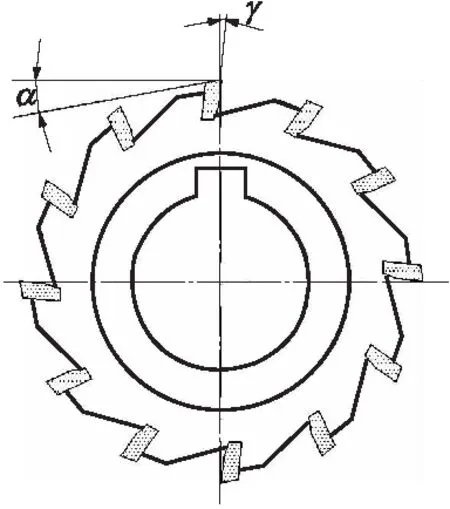
图8 直平面后刀面的三面刃铣刀
盘状刀具直平面后刀面后角参数见图9,AA1为刃口最高点齿背曲线,CC1为刃口最低点齿背曲线,An,Bn,Cn,B1n分别为对应A,B,C,B1点的切削方向,并分别与切削圆半径AO,BO,CO,B1O垂直,前刀面与两齿背平行线相交,作辅助线OA垂直于Am和Cm,由此有以下关系,即

图9 盘状刀具直平面后刀面后角参数
ε1=γfC-γfA
(2)
αfA=ε3
(3)
αfC=ε2=ε3-ε1=ε3-γfC+γfA
(4)
αfB=ε3-εB=αfA-εB
(5)
当αfC=10°时,若εB=5°,αfB=5°,实际上,一般经多次重磨,被磨掉的齿背中心角都大于15°。由此可见,重磨前刀面的直背齿铣刀与前两种齿背曲线铣刀相比,后角的变化很大。为保证重磨后直背齿铣刀有适宜的后角,可采用重磨后刀面方法,也可将后刀面设计成不同后角的两段齿背。
3 圆弧型后刀面
3.1 直柄铣刀圆弧型后刀面的形成
典型圆弧型后刀面刀具结构见图10。圆弧型后刀面的直柄铣刀一般安装到带有偏心孔的夹头上,构成偏心安装后铣刀方能工作。铣刀的切削圆半径和角度参数取决于铣刀在夹头上的安装位置。切削圆半径随装刀位置的变化而变化,一把铣刀可加工出不同尺寸的槽和孔等。

(a)圆弧型后刀面的直柄铣刀
3.1.1 直柄铣刀的圆弧型后刀面各偏心安装参数
如图11所示,夹头回转中心为O,圆弧直柄铣刀轴心为O1,也是夹头偏心孔中心,∠φ=∠AO1X。在图11b中的△AOO1中,AO=RC,AO1=R,OO1=a,形成后角关系为
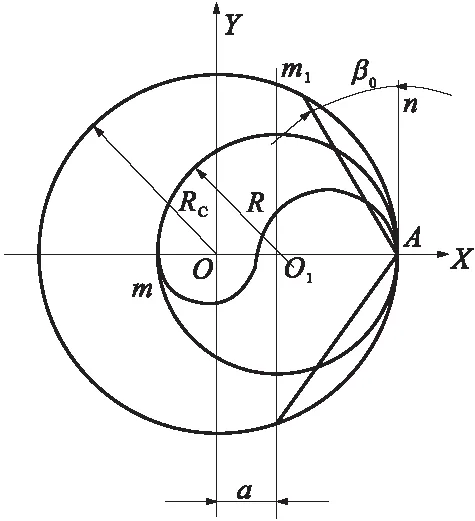
(a)
a2=RC2+R2-2RRCcosα0
(6)
RC2=R2+a2+2aRcosφ
(7)
(8)
(9)
式中,a为装刀孔偏心距(mm);R为圆弧小柄铣刀半径(mm);RC为刃口切削圆半径(mm);α0为刃口后角(°);φ为安装角(°)。
根据式(6)和式(7)绘制坐标曲线(见图12和图13)。由图12可知,安装角φ在0~2π范围内时,切削圆半径RC的范围为(R-a)≤RC≤(R+a)。由图13可知,当φ=π/2时,后角最大,由其结构确定,称为结构最大后角,记作α0jmax。

图12 切削圆半径与安装角关系

图13 后角与安装角关系
将φ=π/2代入式(9)可以得出
(10)
3.1.2 直柄铣刀圆弧型后刀面的偏心安装角
由图13可知实用安装角范围,当安装角φ>π时,α0<0,考虑切削性能对角度参数的要求,在生产中应限定实用安装角范围。
最小后角α0min对应实用最小安装角φmin,有
(11)
如图11c所示,表明圆弧直柄铣刀齿背弧末端m点与刃口A点位于同一切削圆上,m点(R-a)刚好与加工表面产生摩擦,这个位置的安装角称为安全安装角,记作φs,可表示为
φs=180°-ε0/2
(12)
式中,ε0为圆弧柄铣刀齿背弧中心角(°)。
当安装角大于φs时,铣刀与工件碰撞而被折断(见图11d)。
苏霍姆林斯基用鲜活的案例告诉我们,如果孩子学习遇到困难,就应当更多地阅读,阅读能教给他们思考,而思考会变成一种激发智力的刺激。因为孩子思考得越多,其在周围世界看到的不懂的东西就越多,对知识的感受就越敏锐。
最小前角对应的安装角为φrmax,根据切削性能限定的最小前角可以计算出其对应后角α0rmax=90°-β0-γ0min,将α0rmax代入式(10)得φrmax。当α0rmax>α0jmax时,用式(10)计算无解,α0rmax≤α0jmax时有解。
当α0rmax≥α0jmax时,实用最大安装角φmax为
(13)
当α0rmax<α0jmax时,实用最大安装角φmax为
(14)
实用安装角范围为
φmin≤φ≤φmax
(15)
为了方便使用,通常将安装角范围标刻在夹头上,常用安装角范围为30°~50°。
求得实用安装角φmin和φrmax之后,利用式(7)可计算切削圆半径。最小安装角对应最大切削圆半径Rmax,最大安装角对应最小切削圆半径Rmin。
若夹头装刀孔偏心距过大,铣刀不易平衡;若偏心距过小,铣刀后角过小,不能正常工作,因此偏心距的范围应满足
(16)
常取夹头装刀孔偏心距a=(0.3~1)R。
3.2 盘状铣刀圆弧型后刀面的形成
如图14所示,圆弧齿背画法如下:
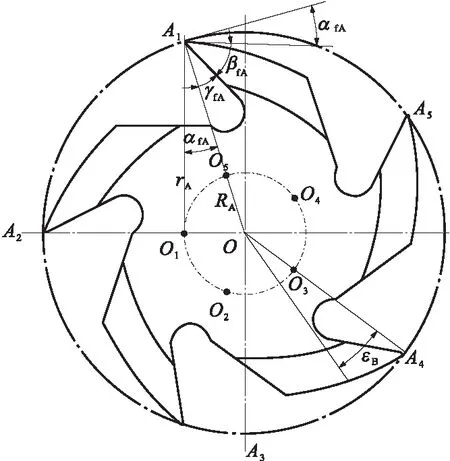
图14 圆弧齿背画法
①根据已知铣刀的最大半径R1画圆,并按齿数Z将圆分为Z等分,得A1,A2,A3,A4和A5点,共5个齿的顶点;
③过A点作射线A1O1,与A1O的夹角,此夹角即为后角αA;
④由齿尖A沿射线取A1O1=rA=qRA,进而得到O1点;
⑤以O1为圆心,rA为半径,过A1点画圆弧齿背曲线;
⑥刃口较低点的齿背圆弧线均是以O1为圆心的同心圆;
⑦以O为圆心,以OO1为半径画圆,以O1为基准点,将该圆分为Z等份,等分点分别为O2,O3,O4和O5;
⑧分别以O2,O3,O4和O5为圆心,以rA为半径,分别过A2,A3,A4和A5画这四个齿的齿背圆弧。
3.2.2 圆弧齿背曲线的后角变化特点
圆弧齿背曲线是相对于铣刀回转中心的偏心圆中的一段圆弧。如图15所示,在大批量生产时可用铲床加工,没有铲床或小批单件生产可在普通车床加工圆弧齿背。

图15 圆弧齿背各点后角
图15中,O为铣刀回转中心,O1为齿背弧圆心,铣刀半径RA=AO,齿背弧半径rA=AO1,A点后角为αfA,齿背曲线上任一点B的后角为αfB,AB的齿背中心角为εB。
(17)
在△BOO1中,有
rB=rA=RAq
(18)
(19)
将式(17)和式(18)代入式(19)得
(20)
当εB=0时,sinαfB=sinαfA,则有
(21)
式中,q为圆弧半径比;αfA为最高刃口点A的后角(°);RA为最高刃口点切削圆半径(mm);ω为相位角(°);a为齿背弧圆心的偏心距(mm)。
由于q,εB和ω为函数关系,而ω又是q的函数,所以sinαfB随εB变化并与q有关。由式(20)绘制坐标曲线(见图16a)可见,在相同工作中心角εB条件下,q的范围不同,曲线位置不同,在不同曲线上αfB与αfA的差值也不同。
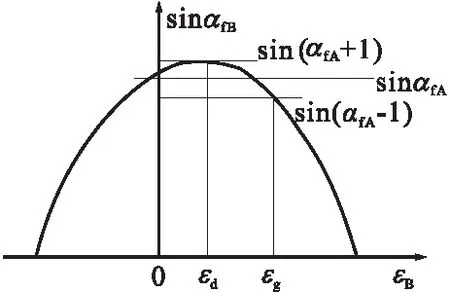
(a)不同q值曲线
当q值固定,εB+ω=90°时,sinαfB取得最大值,对应中心角为曲线的顶点坐标(见图16a中的ωd),由式(21)得
(22)
假定铣刀在工作中心角范围内,αfB≤αfA±1°,如图16b和图16c所示,常用刃口最高点后角αfA=10°~15°,铣刀工作中心角εg=(20%~30%)ε0,经详细分析计算,q值应为0.94~1.03,为了画图方便,取q=cosαfA,1,1/cosαfA为宜。
如图17所示,AO1=rA,AO=RA,CO=RC,在△COO1中,刃口最低点后角为αfC,有

图17 刃口圆弧齿背各点后角
(23)
∠OO1C=180°-ω-αfC-γfC+γfA=180°-(ω+αfC+γfC-γfA)
(24)
(25)
(26)
式中,αfC为C点后角(°);γfC为C点前角(°);γfA为A点前角(°);ω为式(21)中的相位角,利用式(23)计算;RA为A点切削圆半径(mm);RC为C点切削圆半径(mm);q为圆弧半径比;αfA为A点后角(°)。
4 曲面后刀面
曲面后刀面的形式主要是由阿基米德螺线、抛物线、椭圆型等曲线组成的曲面。典型的形式有阿基米德螺线后刀面(见图18a)和抛物线型后刀面(见图18b)。
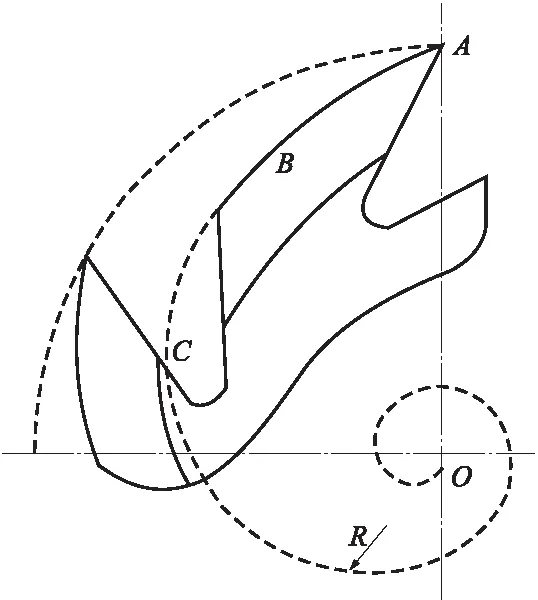
(a)阿基米德螺线后刀面
4.1 阿基米德螺线后刀面刃口和齿背曲线各点的后角计算
阿基米德螺线数学方程式为
R=mθ
(27)
式中,R为极坐标向径(mm);m为单位极角的向径升量或下降量(mm/rad);θ为极角(rad)。
图19为阿基米德螺线后刀面,An,Bn,Cn为切削方向,Am,Bm,Cm为阿基米德螺线的切线,代表刀齿后刀面,ψ为向径OA与切线Am夹角。

图19 阿基米德螺线各点后角
根据高等数学理论,有
(28)

可得
(29)
(30)
m=RAtanαfA
(31)
式中,m为单位转角半径下降量(mm/rad);θA为A点对应的极角(rad);θB为B点对应的极角(rad);θC为C点对应的极角(rad);αfA为A点后角(°);αfB为齿背曲线上B点后角(°);αfC为刃口最低点C的后角(°);RA为刃口A点切削圆半径(mm);RB为齿背曲线上B点切削圆半径(mm);RC为刃口C点切削圆半径(mm)。
在式(29)和式(30)中,因为RA>RB,RA>RC,所以αfB>αfA,αfC>αfA。铣刀经过多次重磨前刀面到齿背B点时,B点便成为铣刀刃口,由于切削圆半径减小,后角ags比原设计后角afA增大。
4.2 阿基米德螺线画法
如图20所示,阿基米德螺线的画法如下:

图20 阿基米德螺线画法
①齿背下降量K的计算式为
(32)
式中,RA为铣刀外圆上最高点所在切削圆的半径,即铣刀直径的一半(mm);m为单位转角半径下降量(mm/rad);ε0为齿距中心角(rad);αfA为刃口最高点A的后角(°);Z为铣刀齿数。
②按已知铣刀最大切削圆直径画圆,并按齿数Z将圆分为Z等份。
③将齿距中心角ε0分为n等份,图20为10等份的示意图,等分点是1,2,3,4,…,10,并连接01,02,03,…,010半径线。
④将齿背下降量K同样n等分,即10等份。
⑥用曲线板圆滑连接1′,2′,3′,…,10′。
⑦作刃口最低点C的齿背曲线,连接OC并延长到1′点,分别从2′,3′,4′沿各半径线方向取C1′长度,用曲线板圆滑连接各截取点即成。
4.3 铲削阿基米德螺线后刀面过程
在铲床上进行阿基米德螺线齿背加工,加工过程称为铲齿。如图21所示,被加工工件铣刀装夹在机床主轴前的夹具上,铣刀轴线与机床主轴同中心。加工时,驱动铣刀匀速旋转,铲床进给机构凸轮也匀速旋转,工作运动开始时,凸轮的I点推动刀架,铲刀刃口位于A,C之间的位置并准备铲齿。

图21 铲齿过程
当铣刀转过ε1角时,铲刀同时匀速进给,使刃口与铣刀前刀面刃口AC点接触并开始铲齿,ε1为铲入角。随着铣刀和凸轮的不断旋转(如图21所示方向),凸轮半径不断增加,推动铲刀进给,当凸轮半径最大点Ⅱ推动刀架时,铲刀进给量为K(齿距中心角范围内齿背下降量),铲刀尖C0点相对铣刀转角为ε1+ε2+ε3=εe,ε2为铲出角;当凸轮继续从Ⅱ点转到I点时,铣刀转过εr角,铲刀退回原位完成一个齿背的一次铲削,εr为退刀角,之后重复此过程。
凸轮上的工作转角ψe,退刀转角ψr与铣刀上的工作角εe,退刀角εr的关系为
(33)
(34)
εe=ε1+ε2+ε3
(35)
式中,ψr为凸轮退刀转角(°);ψe为凸轮工作转角(°);εr为退刀角(°);ε0为齿距中心角(°);ε1为铲入角(°),ε2为铲出角(°),常取ε1+ε2=3°~5°。
5 圆锥后刀面
圆锥后刀面最常见的刀具为标准麻花钻的钻尖后刀面(见图22)。
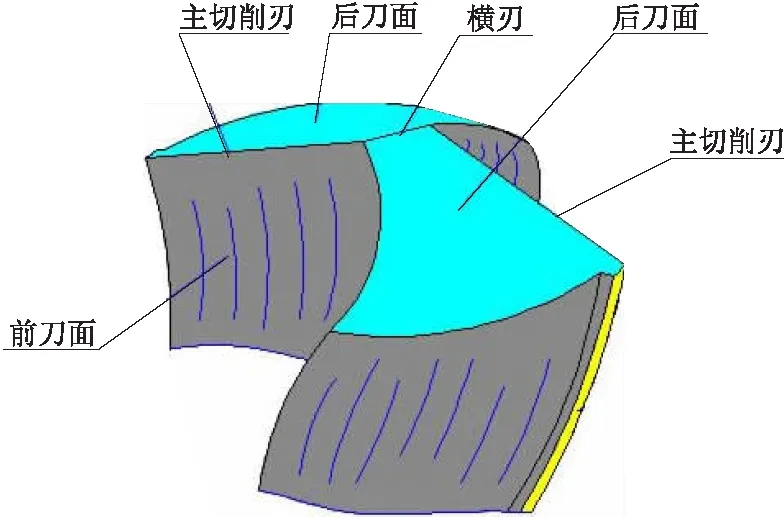
图22 标准麻花钻的钻尖后刀面
5.1 锥面后刀面模型
建立如图23所示后刀面模型,钻头绕Z轴回转形成磨削锥,其半锥角为θ。钻轴与锥轴并不相交,钻头伸出距离为B,钻轴与锥轴轴线的偏距为e,钻轴与锥轴的夹角为ψ。在圆锥面上每个与其轴线垂直的剖面廓形都是圆形,其曲率半径越近,锥顶越小,即曲率越大。利用这一特点,将钻头后刀面作成圆锥表面的一部分,符合钻头后角越靠近钻芯处越大的要求。
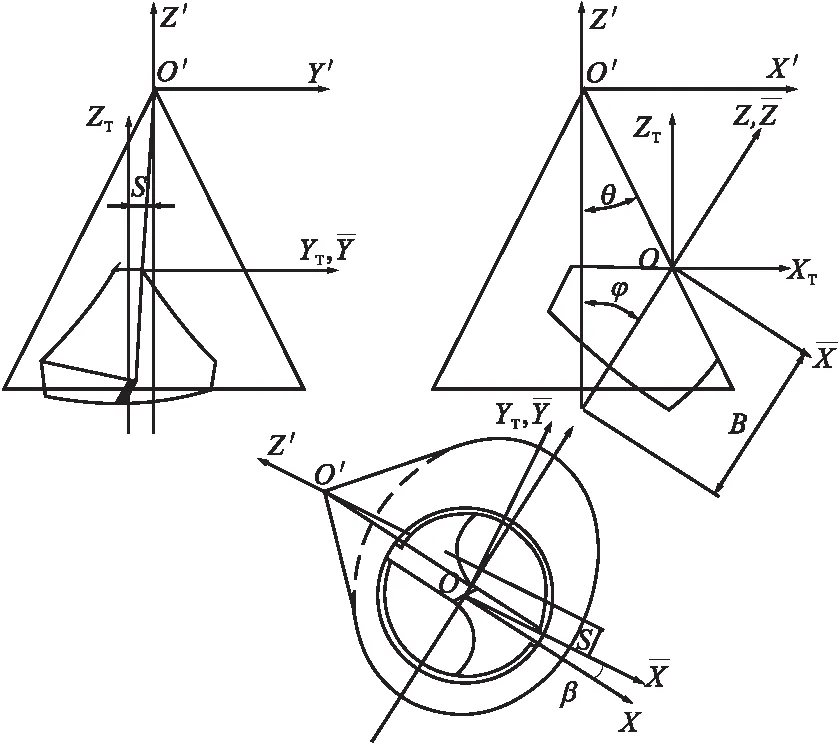
图23 锥面后刀面数学模型
5.2 锥面麻花钻后刀面刃磨运动分析
如图22所示,要在砂轮上磨出锥面后刀面,必须具有:切削加工的主运动,即砂轮回转的运动;锥面形成的运动,为了形成圆锥型磨削面,使钻头绕锥轴往复摆动,进行180°分度从而获得两个对称的圆锥型后刀面;工件进给运动,为了磨去钻头钻尖处的余量,沿工件轴向或与主切削刃垂直方向进给的运动;砂轮修整及补偿运动,正确修整砂轮并对修整量进行补偿,从而获得具有后角的圆锥型后刀面。
5.3 后刀面刃磨参数设计计算分析
根据经验计算可得:θ≈14°,ψ≈45°,e≈(0.12~0.15)d,钻头与钻尖主切削刃的距离约为(1.1~1.5)d。
各刃磨参数对后角的影响随刃磨参数的变化而变化。改变半锥角θ,其余各值作为常量,随着半锥角的增大,后角减小;对于标准麻花钻,顶角2φ=118°,而ψ+θ=φ,故ψ=59°-θ,所以后角随ψ的增大而增大;改变钻头伸出距离B的值,其余各值取作常量,可得随着B的增大,后角增大;同理可求得偏心距e对后角的作用结果,随着e增大,后角也随之增大,且幅度显著。
6 结语
本文列举了常见的刀具后刀面,包括直平面、圆弧面、圆锥面、曲线型面后刀面,通过简述其形成原理及相关角度计算方法,为刀具工作者提供参考。

