基于ALK解法的输流管道防共振可靠性分析
郭 庆, 刘永寿, 白雅洁, 陈翔宇
(西北工业大学 力学与土木建筑学院, 西安 710129)
输流管道广泛应用于航空、航天、航海等领域的大型机械设备之中,工作环境十分复杂。由于流固耦合的作用,管内液体的流速、压力的脉冲都会影响输流管道的固有频率。同时,在管道设计、加工、装配、测量等过程中的不确定性因素导致的几何尺寸、物理参数等的不确定,也会引起输流管道固有频率的不确定性。而一旦输流管道的固有频率与激振力频率相互接近时,将会引发严重的共振失效。此外,航空航天领域的激振力频率通常具有宽频特性,这对于防共振设计也提出了更高的要求。所以,对输流管道进行防共振可靠性分析是十分必要的。
近年来,许多研究人员对输流管道的振动和防共振可靠性进行了大量的研究。Li等[1]把变分迭代方法应用于输流管道的自由振动分析,得到了输流管道在不同边界条件下的临界流速和频率,并且得到了悬壁管在不同流速下的模态形状。韩涛等[2]针对航空复杂液压管路提出了一种直曲组集算法实现了高效建模和模态分析,并且得到了管路布局对“Z”形管固有频率影响的经验公式。翟红波等[3]采用七点估计法计算了均匀流输流管道和非均匀流输流管道的共振可靠度。何新党等[4]分析了考虑状态模糊性时的笛形管在不同水平截集下的结构共振失效概率。张屹尚等[5]通过Kriging代理模型研究了充液管道流固耦合作用下的非概率共振可靠性分析。王忠民等[6]采用Fourior级数展开和微分求积法对弹性地基上输流管道控制方程进行处理得到了时变系统状态方程,通过最优控制原则有效地控制了主参数共振问题。Ritto等[7]提出了考虑建模误差的流体-结构相互作用的概率模型,将输流管道的微分方程通过有限元方法离散化后得到降阶模型,并以得到的随机特征值分析了系统的颤动和发散不稳定模式。Alizadeh等[8]将蒙特卡洛模拟与有限元相结合,应用于输流管道的概率自激振动和稳定性分析,对系统中流体参数随机性效应与管道结构参数的随机性效应进行了比较。张瑞军等[9]采用摄动法分析高速电梯轿厢随机参数对固有频率的影响,通过共振可靠性灵敏度分析评估了各参数对轿厢系统共振可靠性的影响程度的大小。
本文采用近几年来新发展的十分精确高效的主动学习Kriging方法(ALK)[10]进行防共振可靠度的计算,该方法基于Kriging代理模型,通过学习方程“主动”地选择对失效概率影响最大的点加入到实验设计中更新Kriging模型,通过不断迭代直至满足收敛条件。该方法广泛适用于隐式功能函数或有限元等工程问题,对小失效概率、强非线性功能函数、多最可能失效点功能函数等问题也有很好的效果。此外,ALK方法还可以应用于非概率可靠性分析和混合可靠性分析之中。将ALK方法应用于防共振可靠性的突出优点,即在于其筛选出的点均位于激振力频率的上下界附近,在极大提高计算效率的同时,保证了很好的计算精度。
本文将Galerkin加权余量法与ALK方法相结合,通过前者进行输流管道固有频率的计算,再经由ALK方法分析多个不确定性参数影响下的防共振可靠性,并分别计算多个流速下防共振可靠性失效概率的大小,分析管道内液体流速对防共振可靠性的影响,为输流管道的防共振设计应用提供一种新的途径。
1 输流管道模态
本文考虑一长为l的两端简支等直输流管道,假定管内流体无粘且不可压缩,即管内流体均匀流速。根据小变形假设下的Euler- Bernoulli梁模型,我们可以得到输流管道的横向振动控制方程[11-12]
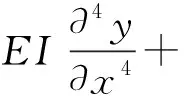
(1)
式中,m0是单位长度管道内流体质量,m是单位长度管道质量,v是管道内的流体流速,EI是抗弯刚度,y是管道横向位移,x是管道轴向位移,t表示时间。控制方程中的各项从左依次表示为弹性恢复力、离心力、科氏力和惯性力。需要指出的是,科氏力是由于考虑了流体的相对流动而出现的,其本质为负阻尼机制,即反对称螺旋阻尼,此时特征值中包含一对共轭复数。
显然,式(1)为高阶微分方程,难以直接求得其解析解,此时可以考虑引入变分法中的Galerkin加权余量法求出其近似解。为了消除时间t的影响,降低求解难度,且管道横向位移为轴向位移x和时间t的函数,不妨假设
y(x,t)=u(x)eiωt
(2)
将y的函数代入式(1),此时可以消去eiωt,可以得到

(m+m0)ω2u(x)=0
(3)
两端简支输流管道的边界条件为

(4)
取满足式(4)的试函数为φj(x)=sinβjx,(j=1,2,…,N),此时的近似解函数为
(5)

将近似解函数(5)代入式(3),可得
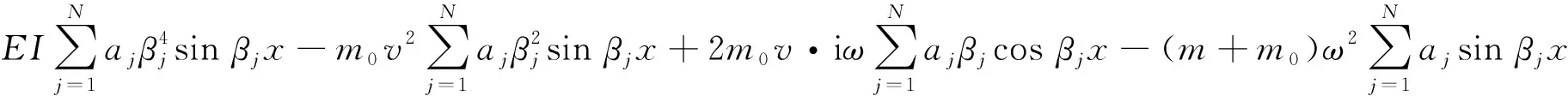
根据Galerkin法规定,权函数与试函数相等,即
Wk(x)=φk(x)=sinβkx,(k=1,2,…,N)
(7)
为了消除余量,作余量与权函数的内积,并令其正交,即
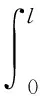
(8)
将式(6)和(7)代入式(8),可得

(9)
其中,g1(j,k)和g2(j,k)分别为
当j=k时,
(10)
(11)
当j≠k时,

(12)
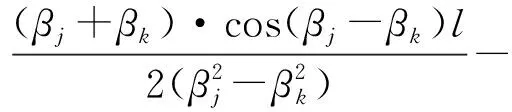
(13)
我们把式(9)称为Galerkin方程组,可以将其写为如下矩阵形式

(j=1,2,…,N;k=1,2,…,N)
(14)
式中,C是Galerkin系数矩阵,属于关于ω的函数。此外
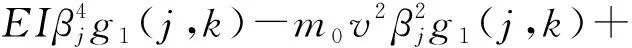
2m0v·iωβjg2(j,k)-(m+m0)ω2g1(j,k)
(15)
显然,式(14)能够取得非零解的充要条件为系数矩阵行列式为零,即
det|C(ω)|=0
(16)
由式(16)可以求出2N个ω,又因为式(15)中含有虚数项,且复特征值共轭出现,再略去实部为负的特征值,可以得到N个ω,其实部为固有频率,虚部为衰减频率。
2 功能函数建立
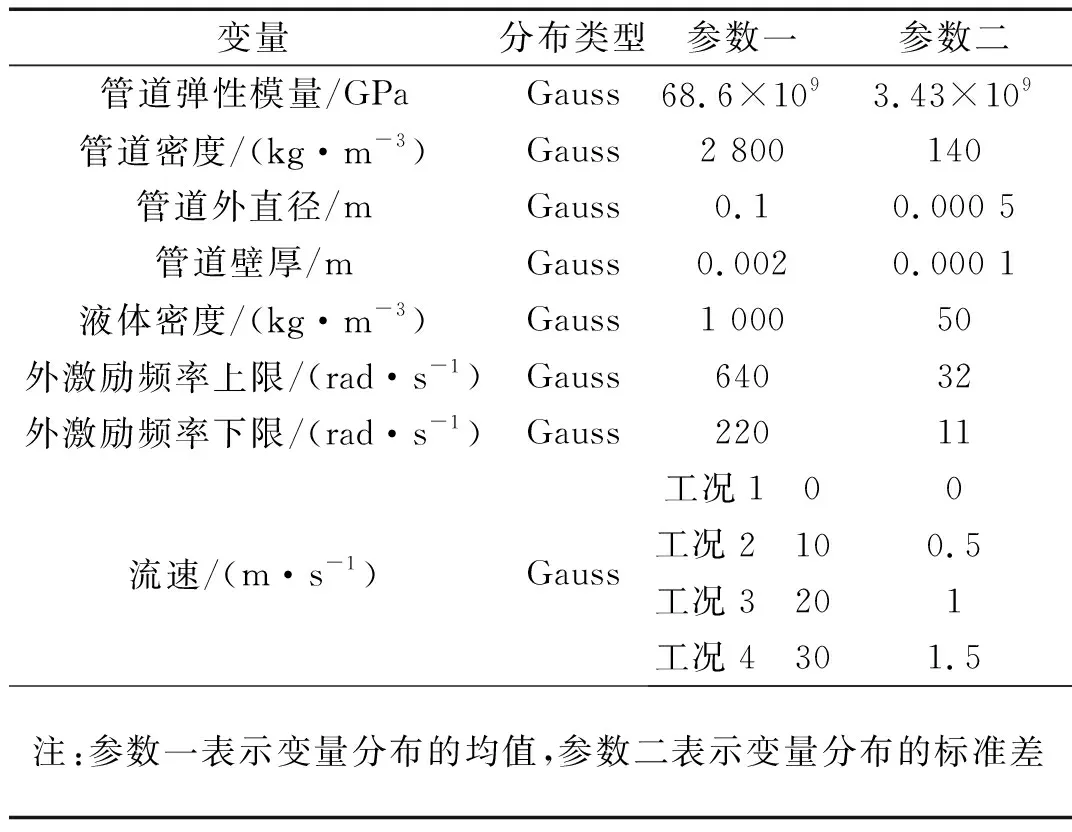
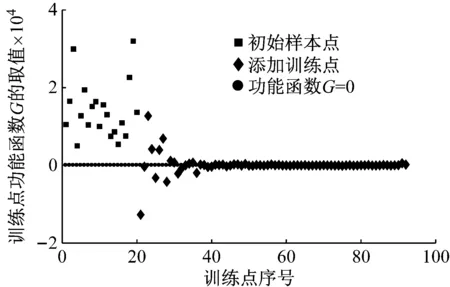
假设固有频率为IF,激振力频率为S,根据传统振动设计规范要求,当1-k1 (17) 式中,mm是管道固有频率所取的阶数,在可靠性中表示失效模式的个数,zjj表示第jj个失效模式,x是随机输入变量向量,IFjj是第jj阶固有频率。 防共振可靠度可以写为 (18) 式中,fx是输入变量x的联合概率密度函数,θx是x的随机分布参数。 式(18)的解析解是很难求得的,通常采用数值仿真或近似解法取得其近似解,最常用的是Monte-Carlo仿真方法,虽然该方法精度很高,但在实际应用中面临计算成本过高,计算效率低这一突出问题。本文采用近年来新发展的主动学习Kriging方法进行防共振可靠性的求解。 本文采用ALK方法求解,下面介绍其相关理论和计算流程。 Kriging模型由两部分组成,前半部分为全局近似,后半部分为局部偏差[13],具体形式如下 G(x)=F(x,β)+z(x)=f(x)β+z(x) (19) 式中,G(x)表示待拟合的目标响应函数,f(x)表示变量x的多项式,β表示f(x)的系数,z(x)表示待拟合函数的随机分布部分。 已知模型(19)里面,F(x,β)代表了全局模型近似,即Kriging模型的均值,也是变量x的多项式函数,一般用f(x)β表示,而在实际中,多项式的形式对于拟合精度的影响几乎可以忽略,所以可简化为常数β。而z(x)代表了局部模型偏差,其统计特征期望为E(z(x))=0,方差为Var(z(x))=σ2,协方差代表了与全局模型的局部偏差的程度,具体形式如下 Cov[z(xi),z(xj)]=σ2R([R(xi,xj)]) (20) 式中,R([R(xi,xj)])是样本点xi和xj之间的相关函数,Kriging模型中使用高斯相关函数,所以又被称为高斯过程模型,其具体形式如下 (21) Kriging模型需要有DoE(Design of Experiment)来求解其相关统计参数,进而才能对目标点进行预测。给定DoE:{x(1),x(2),…,x(n)}(x(j)表示第j个训练点)以及g=[G(x(1)),G(x(2)),…,G(x(n))]T(G(x(j))表示第j个响应),在未知点x处,G(x)的预测值为 (22) (23) σ2rT(x)R-1r(x) (24) 式中,f是n维单位列向量,即1=f=[1,1,…,1],y是n维列向量,含有每个设计点的目标响应值,rT(x)是n维列向量,式(23)和(24)中各参数可由以下各式得到 rT(x)=[R(x,x1),R(x,x2),…,R(x,xn)] (25) (26) (27) (28) 还有就是相关参数θk的值通过最大似然估计求解得到,那么当相关函数是高斯相关函数时,则可转化为下面的优化问题 (29) 相关参数θk的优化可以通过全局优化策略的DIRECT优化算法[14]得到。 基于Kriging模型的传统加点方法都是通过随机抽样得到样本点,进而得到代理模型,那么得到的模型精度必然与所加样本点密切相关,然而盲目地毫无目的性的过多或过少的抽取样本点加入DoE中,都无法保证模型精度。Bichon[15-16]提出了主动学习的方法来选择性地往DoE中添加样本点达到改进模型的作用。Echard等[17]通过结合MC方法提出了主动学习的AK-MCS方法。Yang等提出了一种适用于主客观混合可靠性分析的主动学习Kriging模型。这里采用YANG所提出的ALK方法。 首先考虑预测值是负值,即μG(x)<0,那么此时存在着真实值G(x)>0的风险,定义如下指标来衡量这个风险 R(x)=max[(G(x)-0),0] (30) R(x)表示了μG(x)<0时,G(x)>0的程度,R(x)越大,G(x)越可能被预测错误。此外,已知G(x)是随机变量,那么相应的R(x)也是随机变量。将R(x)进行概率平均,即可得到μG(x)<0时,G(x)的符号预测错误的风险期望 E(R(x))=E[max((G(x)-0),0)]= (31) 式中,μG(x)和σG(x)分别是x点处预测值的均值和方差。φ()是标准正态分布的概率密度函数,Φ()是标准正态分布的累积分布函数。 当预测值是正值,即μG(x)>0,同理,定义μG(x)>0时的风险度量指标为 R(x)=max[(0-G(x)),0] (32) 对应的风险期望为 E(R(x))=E[max((0-G(x)),0)]= (33) 式(31)和(33)可以写成统一形式,即 E(R(x))= (34) 式(34)即为风险期望方程(ERF),或者称为学习方程。ERF表示了G(x)的预测值与真实值间符号不同的可能性的大小,即ERF值越大,在该点处G(x)的真实值由正变负或由负变正的可能性就越大。此外,ERF值比较大的点一般都是在极限状态曲面附近的点和Kriging方差很大的点,所以,我们应该将这些ERF值最大点选出来加入到DoE中,从而提高Kriging模型的拟合精度。 步骤1在各随机变量组成的不确定性域中随机抽取Xt=(X1,t,X2,t,…,Xn,t)(t=1,2,…,N)个初始样本点,计算功能函数值,构建初始Kriging模型,此处N=20。 步骤2随机产生大量候选样本点,为ERF方程选点做准备,为使候选样本点充满不确定性域,取候选点数量为m=105。 步骤3在候选点中计算Kriging模型的预测值μG(X)和ERF值,将ERF值最大的点记为X*。 步骤4若ERF最大值满足收敛条件的阈值,则转入步骤6,本文阈值大小为10-3。 步骤5若步骤4中的收敛条件无法满足,将X*加入DoE中,并计算X*处的功能函数值更新Kriging模型,返回到步骤3。 步骤6基于已建立的Kriging模型,代入Monte-Carlo法中求解防共振失效概率。 本文以两端简支输流管道为模型进行计算验证,如图1所示。管道长度l=2.0 m,外直径D=0.1 m,壁厚δ=0.002 m,管道所用材料弹性模量E=68.6 GPa,密度pd=2 800 kg/m3,泊松比ρ=0.3,管道内液体密度fd=1 000 kg/m3。 图1 两端简支输流管道模型 根据Galerkin加权余量法计算求得的输流管道在不同流速下的前四阶固有频率如表1所示,可以发现随着管道内液体流速的增加,各阶固有频率均逐渐下降,其中,一阶固有频率下降最多。该现象主要因为随着液体流速的增大,使管道刚度不断下降,进而引起固有频率的不断减小。 表1 输流管道的前四阶固有频率 然后,根据ALK方法计算防共振可靠性。为考虑流速对防共振可靠性的影响,分为四种工况进行计算,分别为:① 流速的随机分布类型为正态分布,变异系数为0.05,后面三种工况的分布类型与参数与工况1相同,流速大小均值为0;② 流速大小均值为10;③ 流速大小均值为20;④ 流速大小均值为30。影响防共振可靠性的各随机变量如表2所示。 防共振可靠性计算结果如表3所示。由结果可以知道,随着液体流速的增大,一阶固有频率共振失效概率不断减小,而与此相反的是,二阶固有频率共振失效概率不断增大。根据李占营等[18]的结论,流速增大会导致刚度减小,进而导致固有频率降低,在此表现为一阶固有频率不断远离外激励频率,而二阶固有频率不断靠近外激励频率。此外,如图2所示,经ALK方法选出的训练点的外激励频率的上限和下限分别分布在640 Hz和220 Hz左右,有利于提高防共振可靠性失效 表2 输入变量的随机分布类型及参数 概率的计算精度。ALK方法除20个初始样本点外,通过ERF方程主动选点的收敛速度是十分快的,以工况2的一阶固有频率防共振可靠性计算为例,共筛选出81个功能函数正负号预测错误风险最大的训练点,且大部分训练点都位于极限状态附近,提升了对目标功能函数的预测精度,同时也极大地提高了计算效率,如图3所示。所以,相对于其它传统可靠性求解方法,如Monte-Carlo法、点估计法和响应面法等[19-20],ALK方法能够在保证共振可靠性计算精度的前提下,极大地减少功能函数的调用次数,提高失效概率的计算效率。但需要注意的事,ALK方法对于初始样本点的依赖较高,需选用均匀性很好的抽样方法。此外,ALK方法对于高维问题求解尚存在困难。 表3 不同工况下防共振可靠性分析结果 图2 工况2下ALK方法所取训练点外激励频率分布 Fig.2 The external excitation frequency distribution of training points obtained with ALK solution under condition 2 图3 工况2下ALK方法得到的DoE 本文考虑输流管道在流固耦合作用下,联合Galerkin加权余量法和ALK方法,建立了一种新的输流管道防共振可靠性分析方法,并以两端简支输流管道为例进行了计算验证分析。首先,固有频率计算结果证明输流管道内液体流速的增大会影响管道固有频率不断下降。同时,防共振可靠性分析结果证明管道液体流速的增大会不断影响管道一阶固有频率不断远离外激励频率范围,二阶固有频率不断靠近外激励频率范围。本文中共振可靠性功能函数为隐式、非线性的,算例证明了所提方法能够有效地处理含隐式、非线性功能函数的复杂工程问题,为输流管道的防共振可靠性分析提供了参考。3 防共振可靠性分析
3.1 Kriging插值模型

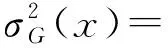
3.2 ERF学习方程
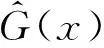
3.3 ALK方法的基本步骤
4 算 例




5 结 论

