混凝土直切槽平台巴西圆盘冲击劈裂拉伸断裂特性试验和数值模拟研究

张 华, 郑 凯, 王 雷

(河海大学 土木与交通学院，南京 210098)

由于材料抗拉性能不足，工程中混凝土大多是带裂缝工作的。结构的破坏实际上是材料中微裂纹萌生和扩展的宏观表现。在高应变速率下，混凝土内部裂纹萌生位置和扩展路径不同，材料的断裂和损伤特性也有较大差异，这导致了更加复杂的结构破坏。深入研究不同冲击条件下混凝土拉伸破坏的裂纹演化和损伤机理，能够为建筑物的抗爆和抗震设计提供有价值的参考。

一些学者通过间接拉伸试验方法来研究材料的抗拉特性[1-6]。其中，巴西试验因方法简单而被广泛应用。巴西试验能够对材料力学性能、裂纹演化、损伤和断裂特性进行多方面研究[7-9]；同时，巴西试验也适用于动态冲击的加载条件。分离式霍普金森压杆(Split Hopkinson Pressure Bar, SHPB)是动态力学研究中最重要的试验技术之一。经过几十年的发展，新型的分离式霍普金森压杆不仅可进行压缩试验[10]，还可进行层裂试验[11]、三点弯曲试验[12]、冲击屈曲试验[13]和劈裂拉伸试验[14-15]。文献[16]采用SHPB对混凝土进行了劈拉试验，认为应变率对材料的力学性能和裂纹演化有一定影响。文献[17]通过动态劈裂拉伸试验，认为试件破坏模式、临界破坏时间是影响动态起裂韧度的重要因素。文献[18]在对应变率的研究中，发现试件内部应力波扩展存在时间效应和惯性效应，这导致了极其复杂的裂纹演化规律，高应变率下很难保证巴西试验主裂纹的破坏形式。Chen等[19]通过实现圆弧加载方式进行了更为深入的研究，得出了降低试件局部破坏的合适加载角，保证了试件主裂纹的断裂形式。然而，上述研究工作并不能给出裂纹演化进程中试件内部应力的分布与传播。

数值模拟研究可以从应力分布角度解释试件破坏进程中的裂纹演化。其中，有限单元法(FEM)[20-22]对网格划分的处理增加了计算成本，裂纹只能沿单元边界扩展，具有一定局限性。而其它方法，如离散元法(DEM)[23-25]、混合有限元/离散元法[26]和非连续变形分析(DDA)[27]一定程度上弥补了传统有限元的不足，但这类方法只能给出定性的破坏模式，对开裂进程模拟精度不够。另外，扩展有限单元法(XFEM)既继承了有限元的所有优点，又能足够精确反映裂纹演化进程。由XFEM提供的水平集法，可以使用高维度集曲线反映裂纹界面变化，从而实现裂纹在单元内部扩展。Sukumar等[28-29]利用XFEM对二维平面裂纹扩展进行模拟并将其推广至三维模型。文献[30]将扩展有限元的粘聚裂纹模型与通用有限元耦合，再现了混凝土梁的复合开裂进程。Gregoire等[31]对SHPB试验进行了数值模拟，证实了XFEM同样适用于复杂波形加载条件。扩展有限元为巴西试验中裂纹演化进程的数值模拟研究提供了可能。

本文采用改进的SHPB设备，对含复合型裂纹CSTFBD试件进行了动态劈裂拉伸试验，从理论和试验结果分析了不同水灰比、不同加载速率、不同预设裂纹倾角和长度对材料断裂韧性和破坏模式的影响；利用XFEM进行数值模拟，得出裂尖扩展与应力变化的时域关系，再现了裂纹演化的完整过程。

1 试验概况及原理

1.1 试件制备及实验过程

动态劈拉试验考虑了三种不同混凝土强度，具体配合比见表1。

表1 混凝土配合比参数表

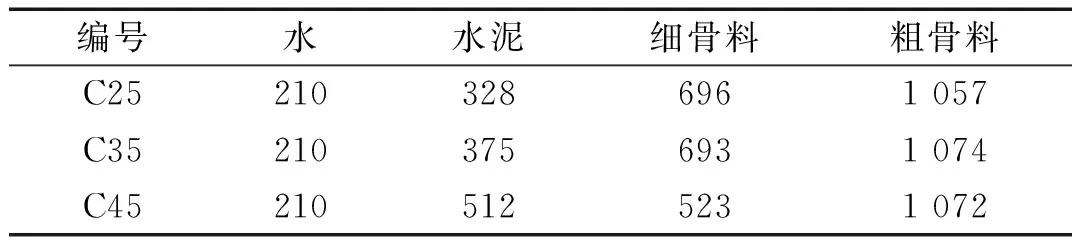
Tab.1 Mix proportions of materials in specimenskg/m3

水泥采用南京海螺牌32.5级普通硅酸盐水泥，细骨料为粒径0～3 mm，粗骨料最大粒径在10 mm以内。将拌匀的混凝土放置在300 mm×300 mm×1 200 mm的模板内振捣均匀，在标准养护室(温度为20±3 ℃，95%相对湿度)养护28天。之后，通过取芯机和打磨机制备成尺寸为Φ74 mm×30 mm的圆柱试件，并在试件上下端切削20°的平台。试件的几何参数示意图见图1。图中,2a是预设裂纹长度，R是半径，2β是平台的加载角度，t是试件厚度，D是圆盘直径。考虑预设裂纹长度和倾角两个因素，将倾角为0°、10°和20°的试件用于测试材料断裂力学性能，同时将0°，30°和60°的试件用于材料破坏模式的研究，每种工况下测试3个试件。

图1 CSTFBD试件的几何参数示意图

准静态劈拉试验通过电子控制液压万能试验机实现，采用0.02 mm/min的位移控制加载，应变率为10-5s-1量级。动态劈拉试验采用Φ74 mm的分离式霍普金森压杆，入射杆为长3 200 mm、Φ37 mm～Φ74 mm过渡的杆件，透射杆长1 800 mm，仪器工作原理如图2。子弹经预设的气压加速撞击入射杆，在入射杆内产生压缩波并经过试件扩展至透射杆。在压杆上布置应变片来捕获入射波、反射波和透射波，并在试件中心横向布置应变片以求得试件破坏时的应变率。不同应变率的加载通过氮气调压阀来实现。

图2 SHPB劈裂拉伸试验工作原理

1.2 CSTFBD试件动态应力强度因子

断裂力学中，应力强度因子(Stress Intensity Factor, SIF)是反映裂纹尖端弹性应力场强弱的物理量。实验表明，当应力强度因子达到某临界值时，裂纹失稳扩展导致断裂，此时的临界应力强度因子即为断裂韧性。巴西试验的破坏以I型裂纹和II型裂纹为主。如图3，对承受2γ加载角、大小为σ均布荷载的巴西试件，以圆心和AB轴为零点建立极坐标系(r,θ)，根据力的平衡条件，合力为

(1)

(2)

图3 均布荷载下直切槽巴西圆盘计算简图

(3)

(4)

系数Aji(j=1,2,3;i=1,2,…,n)可通过三角函数来表示，fji(j=1,2;i=1,2,…,n)也可表示为

A1i(θ)=icos(2iθ)-icos(2(i-1)θ)

(5)

A2i(θ)=isin(2iθ)-(i-1)sin(2(i-1)θ)

(6)

(7)

cji可通过文献[32]计算出。将式(3)和(4)积分并代入系数后整理出

(8)

(9)

其中系数

(10)

sin[2(i-1)θ0]sin[2(i-1)γ]

(11)

对应力强度因子做无量纲化处理，得到

(12)

(13)

通过数值分析得到I型、II型无量纲化应力强度因子FI、FII的关系曲线(如图4、图5)。可见复合型裂纹中，FI与预设裂纹倾角呈负相关；随预设裂纹长度的增加，倾角15°以下试件的FI有一上升段，15°以上试件的FI持续下降，但最终都表现为下降趋势。FII随裂纹长度和倾角的增加都表现为持续的增加趋势。

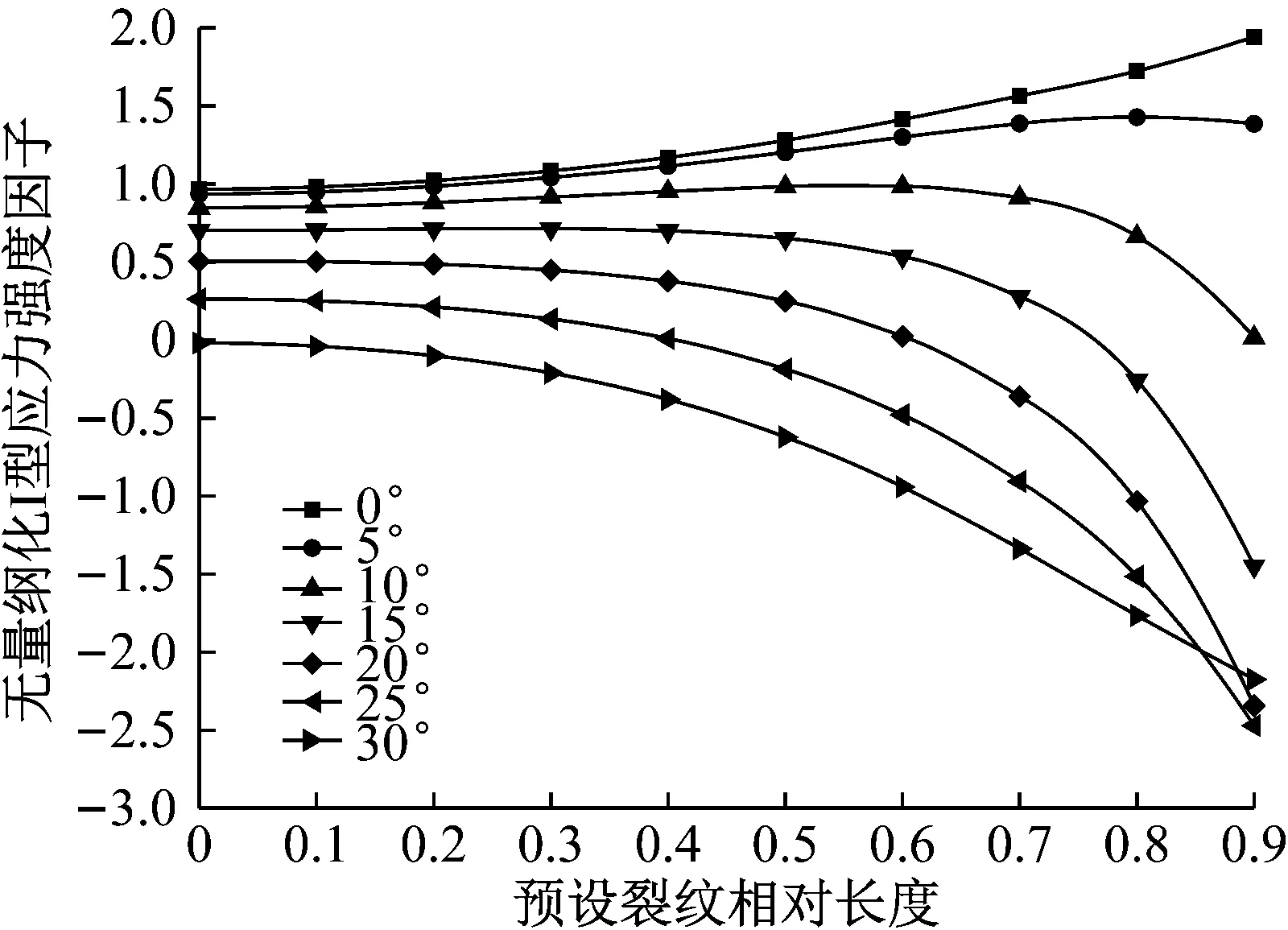
图4 I型裂纹无量纲化应力强度因子曲线图

图5 II型裂纹无量纲化应力强度因子曲线图

(14)

Pi(t)=EbAb[εi(t)+εr(t)]

(15)

Pt(t)=EbAbεt(t)

(16)

(17)

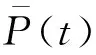
θΠ=30.982-6.666 7α-19.048α2

(0.1<α<0.9)

(18)

当倾角0°<θ<θΠ时，该裂纹即为复合型裂纹。本研究相对预制裂纹长度α=0.25，其临界倾斜角为28°，试验设计的10°和20°裂纹倾角可被认定为复合型裂纹。

2 CSTFBD试件断裂韧性及破坏形态

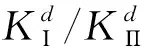
图6 不同工况下试件的荷载-时间曲线(2a=9.25 mm)

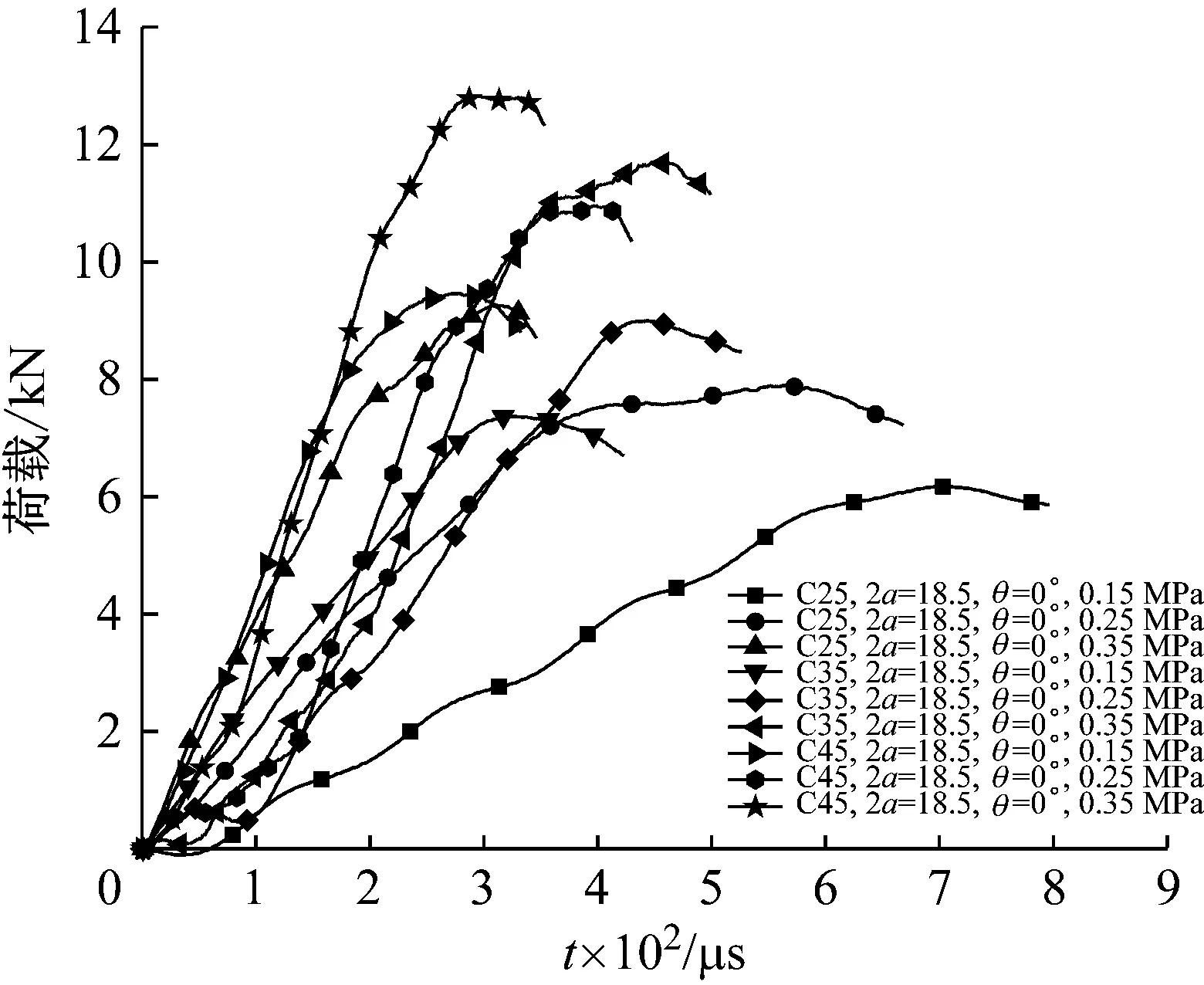
图7 不同工况下试件的荷载-时间曲线(2a=18.5 mm)

图8 不同工况下试件断裂韧性统计图

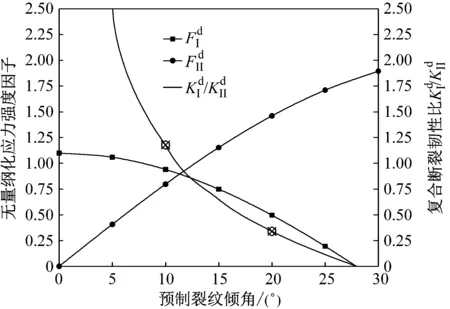
图9 裂纹倾角复合断裂韧性影响关系曲线(α=0.25)

为进一步研究倾角对裂纹分布的影响，选用30°和60°大倾角CSTFBD试件进行分析。加载气压为0.15 MPa和0.25 MPa，预制裂纹长度为9.25 mm。试件破坏后主裂纹的分布情况如图11。

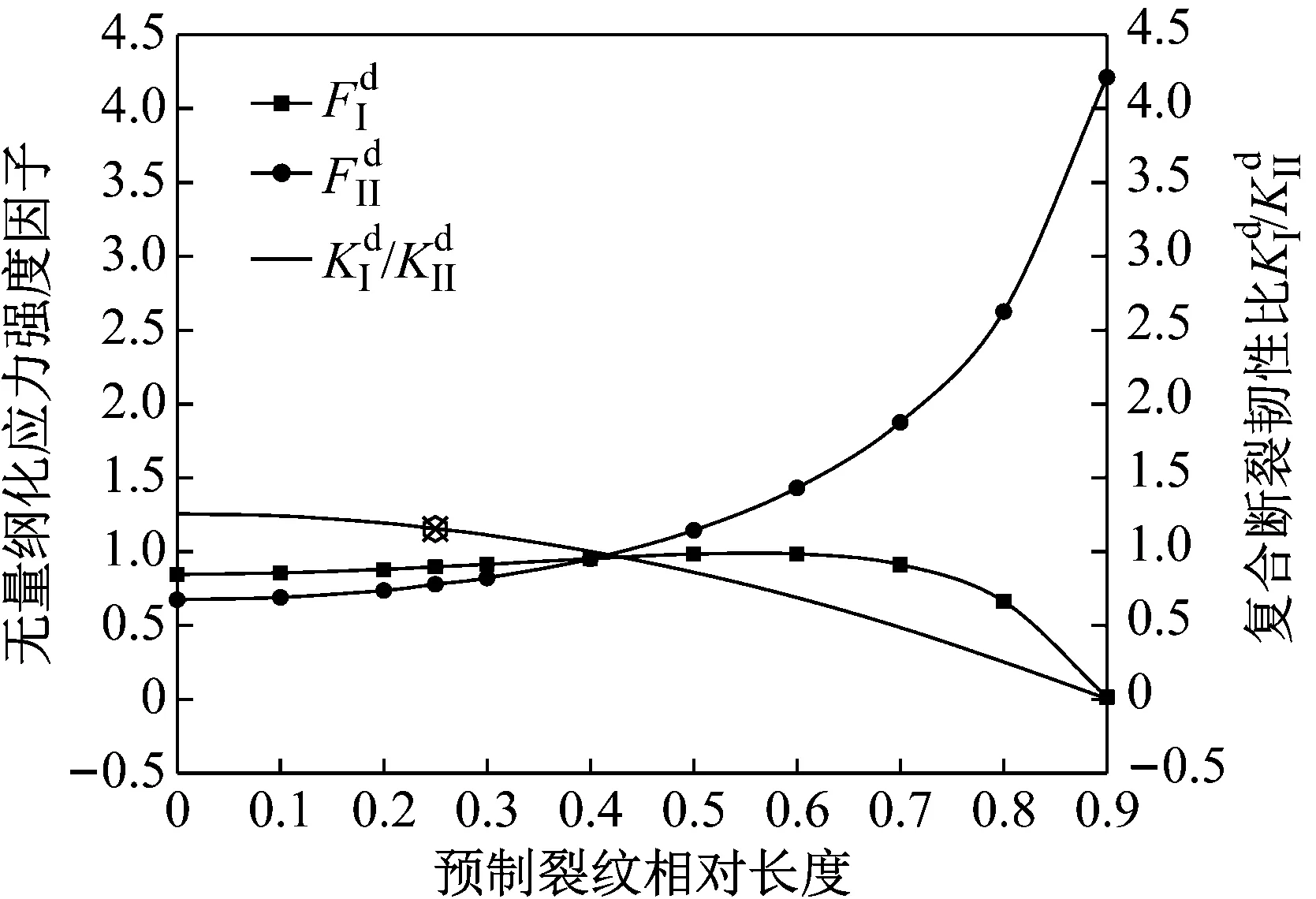
图10 裂纹长度复合断裂韧性影响关系曲线(θ=10°)

图11 不同情况下试件的典型破坏模式

从图11中可以看出，含纯I型裂纹试件(裂纹倾角为0°)的破坏为单一主裂纹破坏，裂纹沿加载点和预设裂纹方向开裂并贯通，是巴西试验的典型破坏特征。当预设裂纹倾斜角为30°和60°时，加载端仍有一条裂纹，而约束端出现一条次生裂纹。次生裂纹随倾斜角的增加，扩展方向与预制裂纹角度逐渐一致。当应变率增加时，加载端会产生一个碎裂带，同时主裂纹宽度有所增加。这是由于应变率增加时，加载端部的摩擦力作用明显，该区域受力情况变复杂，大量的微裂纹同时扩展贯通，最终导致碎裂带的产生，这也是动荷下力学特性增强的原因。

3 扩展有限元数值模拟

数值模拟采用扩展有限单元法(XFEM)，对预设裂纹倾角为30°和60°的CSTFBD试件进行模拟，得出试件破坏过程中应力分布和裂纹扩展的关系，再现了试验中的裂纹演化进程。扩展有限单元法的思路是将扩展函数插入到有限元的位移求解中，以反映裂纹的不连续面。改进后的单元节点位移表达式为

(19)

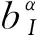
(20)

式中:x为某集成点;x*为距离x在裂尖位置最近的点;n为x*点的单位法线。Fα(x)通过位移场基函数解释了裂纹尖端的奇异性

[Fα(x),α=1 to 4]=

(21)

式中,(r,θ)表示从位于裂纹尖端的极坐标系统上的坐标值。

研究基于损伤力学模型，采用ABAQUS对试件的断裂问题进行求解。损伤模型建立在裂纹表面的牵引分离法之上，当满足最大主应力准则后开始产生损伤，即：

(22)

损伤演化准则通过引入损伤变量D来判定损伤演化。单元法向及切向应力分量受损伤影响表达式为

(23)

ts=(1-D)Ts

(24)

tt=(1-D)Tt

(25)

式中:D∈(0,1)代表裂缝间的平均损伤值;tn、ts和tt分别为法向应力向量t和两切向应力分量；Tn为弹性条件下受力单元法向应力分量;Ts和Tt分别为受力单元第一和第二切向应力分量。

对C35等级混凝土进行试验[34]，试验结果用于定义数值模拟中的材料参数。定义材料为理想的线弹性材料，材料密度为2 500 kg/m3，轴心抗拉强度为1.43 MPa，杨氏模量为34.4 GPa，泊松比取0.2。有限元模型采用C3D8R单元，损伤演化选取基于能量的、线性软化的及混合模式的指数损伤演化规律，断裂能参数设置为160 N/m。考虑大变形后进行几何非线性分析，并将模拟结果同试验结果进行比对(如图12)，证实了数值模拟的有效性。预置裂纹倾角为30°和60°试件中裂纹扩展和应力分布计算结果如图13和图14。

图12 试验和扩展有限元所得应力强度因子对比

Mises Stress Nephogram

Maximum Principal Stress Nephogram

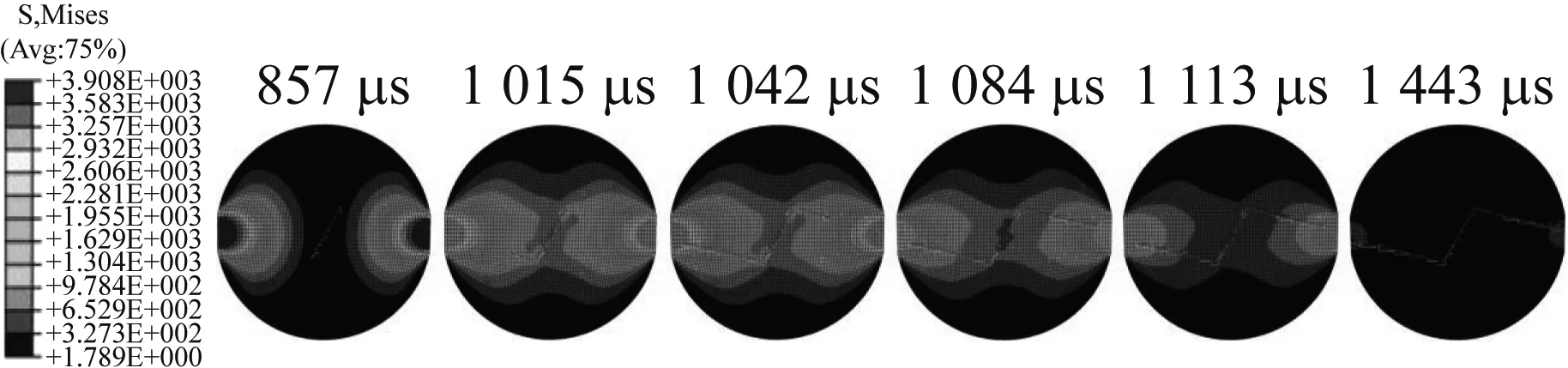
Mises Stress Nephogram

Maximum Principal Stress Nephogram

由图13和图14可知，裂纹开展前期，试件平台端有较大应力。当最大主应力区达到裂纹端部时(1 004 μs和1 015 μs)裂纹开始扩展。开裂使有效应力得到一定程度的释放，但在加载后期(1 151 μs和1 084 μs)最大主应力再次增加，并随着裂纹贯通试件后(1 248 μs和1 443 μs)，降为低应力状态。预制裂纹的倾角对应力分布也有一定影响。含30°倾角模拟结果中，有效应力始终保持低水平状态，试件两端应力波在向中部传播时随开裂被释放，裂尖范围始终处于较高应力状态。含60°倾角的试件在开裂前有效应力分布较为均匀，裂尖端范围内应力集中相对较小。

对比试验中试件的破坏形态，数值模拟结果没有产生破碎带和次生裂纹。这是由于XFEM方法中，裂纹只能沿预设裂尖开展，而现实条件下试件存在大量微裂纹和孔洞，这些缺陷可同时进行开裂。而根据巴西试验中心起裂和主裂纹破坏的前提条件，数值模拟结果又是有现实意义的，它指出了次生裂纹的起裂位置并非在预设裂尖：分别在1 151 μs和1 084 μs中，试件内部最大应力二次增加，高水平的应力区域扩展至试件端部，导致试件边缘开裂，从而产生次生裂纹。可以认为，次生裂纹是由端部沿着应力集中区段边缘扩展至预设裂纹尖端的。整体而言，XFEM方法能够较好还原试验结果，并且能够从应力场的角度解释裂纹的演化进程，探究高速冲击下材料的破坏规律。

4 结 论

对含复合型裂纹CSTFBD试件进行了劈拉试验，结合理论分析了不同水灰比、不同应变率、不同预设裂纹长度和倾角对试件断裂韧性的影响。采用XFEM模拟了不同预置裂纹倾角试件中裂纹的开裂进程，并与试验结果进行了对比。得出以下结论：

(1) 试件的断裂韧性随强度等级、加载速率的增加而增加，预制裂纹长度对动态断裂韧性的影响很小，但是倾角影响较大。复合断裂韧性比与裂纹倾角及长度呈负相关，但它与应变率的变化无关。当预制裂纹长度一定时，随倾斜角度的增加，裂纹由I型向II型变化。

(2) 含纯I型裂纹的试件破坏时无次生裂纹产生，其他情况下都有次生裂纹产生。次生裂纹的出现降低了试件的断裂韧性。较大应变率导致试件端部形成的碎裂带是由于复杂受力环境下微裂纹的扩展，属局部失效模式。

(3) 预设裂纹倾角越大，试件内部有效应力越均匀、裂尖范围内应力集中越小、主裂纹发展越缓慢。主裂纹开裂后试件内部应力都有再增大并扩展至试件端部的过程，这种情况导致了次生裂纹。次生裂纹是从试件端部扩展至裂尖的，这一点与主裂纹的开裂进程相反。

(4) 扩展有限元方法能够模拟出导致试件破坏的主裂纹分布，并能够从应力的角度对裂纹的扩展进程进行解释。这种方法较好再现了试验过程，但对其他因素(如考虑细观非均质性[35]、考虑多裂纹扩展分析)的研究尚需要进一步深入。