基于Tikhonov正则化迭代求解的结构损伤识别方法

夏志鹏， 王树青， 徐明强， 王皓宇

(中国海洋大学 海洋工程系， 山东 青岛 266100)

海洋平台结构长期服役在恶劣的海洋环境中，容易产生各种形式的损伤，使结构的承载能力下降，甚至导致平台失效，造成巨大经济损失及人员伤亡[1]。因此，针对海洋平台结构的健康监测与损伤识别非常重要。目前结构损伤检测的方法众多[2-3]，基于振动测试的结构健康监测技术相对较为简单且成本较低，是非常具有发展前景的损伤识别技术[4]。其中，基于模态参数的损伤检测是近年来新兴且有效的检测手段。

在某些情况下，基于模态参数的结构损伤识别过程可以简化为线性方程组Cα=b的求解问题。当不考虑测量噪声或噪声干扰较小时，该系统的求解往往可以得到满意的结果；而当结构测量模态信息受噪声影响较为严重时，系统的求解结果往往会振荡发散，导致检测方法失效。因此，噪声鲁棒性是此类损伤识别技术在发展过程中必须考虑的问题。

从数学的角度看，利用结构的振动测试数据识别其损伤是求解反问题的过程，其不适定性体现在所构建系统的病态上，即微小的测量误差都可能导致解的振荡发散。为解决这一问题，学者们做了大量研究[5-11]。其中，基于Tikhonov正则化[12]的方法应用较为广泛，其基本思想是：用一族与原问题相“邻近”的适定问题的解去逼近原问题的真实解。王艺霖等将Tikhonov 正则化方法用于结构的损伤识别，一定程度上改善了系统的不适定性，提高了损伤识别精度，并指出正则化方法的作用可通过刚度矩阵条件数的减小来明确衡量。Hua等将Tikhonov正则化与基于灵敏度分析的有限元模型修正方法相结合，进行了简单框架结构的损伤识别，该方法体现出较好的抗噪性。应用Tikhonov正则化虽然能在一定程度上抑制噪声，改善损伤识别结果的稳定性，但它的解是过度光滑的，不具有稀疏性[13]。换言之，应用该方法虽然能筛选出真实的损伤信息，但也引入了过多的虚假损伤信息，给损伤识别带来困难。为改善这一问题，张纯等[14]在Tikhonov罚函数项中引入光滑函数，并结合基于灵敏度分析的模型修正方法进行损伤识别研究，明显改善了损伤识别效果；张纯等[15-16]先后将L1和L1/2范数正则化模型修正方法应用于结构损伤识别，有效地改善了基于Tikhonov正则化损伤识别结果过度光滑的缺陷。

利用正则化方法求解线性不适定系统，关键在于正则化参数的选择。上述正则化及其改进方法大都采用L曲线法选取正则化参数，而L曲线的绘制过程往往需要进行大量的试算，对于大型的结构系统，试算过程更加复杂。对于Tikhonov正则化，其参数的合理取值范围一般较小，系统求解效果对正则化参数的依赖性很高，并且当噪声水平较高时，L曲线趋于平直，很难通过该方法选取合适的正则化参数[17]。

解的过度光滑及正则化参数选择时试算量过大是制约Tikhonov正则化应用于损伤检测的两大难题。对此，本文综合上述正则化方法的优势及缺陷，提出了一种基于Tikhonov正则化的迭代求解方法，用于测量噪声影响下损伤识别线性系统的求解。该方法基于Tikhonov正则化理论，能够在迭代过程中利用二分法自适应调整正则化参数，并通过迭代的方式重构正则化权重矩阵，能够充分抑制噪声，保留实际损伤信息。通过一个数值算例，验证了本文方法的有效性。

1 基本理论

1.1 交叉模态应变能方法

交叉模态应变能(CMSE)方法[18-21]是一种典型的以线性系统求解结构损伤信息的识别方法。该方法计算简单，并且可以同时识别结构的损伤位置和损伤程度。与其他的检测方法相比，该方法有如下优点：不需要质量归一化的振型；仅利用结构损伤前后的较少几阶模态即可判断结构的健康状况。因而，应用CMSE方法进行损伤检测具有很好的发展前景。

设K和M分别为结构刚度和质量矩阵，λi和Φi分别表示第i阶特征值和特征向量。结构损伤前后的特征方程可表示为

KΦi=λiMΦi

(1)

(2)

本文中，上标“*”用来表示损伤后的情况。

(3)

(4)

对式(3)两边取转置，并考虑矩阵K和M的对称性得

(5)

联立式(4)、(5)，并考虑到M*=M，可以得到：

(6)

本文中，单元损伤通过杆件模量的等效折减进行模拟，即对第n个结构单元，其损伤后的模量值

(7)

式中，En为损伤前第n个单元的模量，αn为相应的损伤程度。则损伤后结构的刚度矩阵可写为

(8)

式中：Ne为结构单元的总数；Kn为第n个单元损伤前的单元刚度矩阵。

将式(8)代入式(6)并整理后得

(9)

用Ni和Nj分别表示结构损伤前后的模态阶数，可以构建Nq=Ni×Nj个线性方程，将其写成矩阵形式

Cα=b

(10)

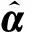
(11)

可采用奇异值分解法(SVD)寻求最小二乘解。对系数矩阵C作奇异值分解

(12)

(13)

当测量模态空间不完备时，采用Guyan扩阶法[22]对不完备振型进行如下扩阶处理

(14)

1.2 Tikhonov正则化方法

Tikhonov方法的思想是将最小二乘解和最小范数解综合考虑。对于式(9)所示的线性系统，可建立目标函数如下

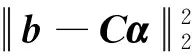
(15)

其中L为Ne阶正则化矩阵，一般作变换将L转化为单位矩阵I[23]。ξ为正则化参数，用于控制最小二乘解和最小范数解之间的平衡。

当L为单位矩阵时，式(14)等价于求解

(CTC+ξ2I)α=CTb

(16)

该方程的解为

(17)

对系数矩阵C作式(11)所示的奇异值分解，则式(17)可表示为

(18)

其中

(19)

称为Tikhonov过滤因子，显然，f(σi)的大小依赖于奇异值σi和正则化参数ξ。而当ξ≪σi时，式(18)转化式(13)所示的最小二乘解。

2 基于Tikhonov正则化的迭代求解方法

Tikhonov方法的正则化矩阵一般为单位矩阵，这表明Tikhonov正则化方法对各单元损伤参数进行了相同的加权平滑处理，其解不具有稀疏性。而对于损伤结构而言，其损伤参数是稀疏分布的，即除个别损伤单元外，解向量的大部分元素均为零。因此，传统的Tikhonov正则化应用于损伤检测时存在一定的缺陷。适合损伤识别的理想正则化方法应具有如下特性：对于真实的损伤信息，正则化的平滑作用较小以便保留结构的实际损伤信息，即正则化矩阵中对应的权重较小；当出现虚假损伤时，增强平滑作用以消除噪声导致的虚假损伤信息，即正则化矩阵中对应的权重较大。为了达到这一效果，本文考虑通过具有稀疏性的损伤参数来重新构造正则化矩阵，构造形式如下

L(α)=diag{(|α1|+ε)-1,…,(|αn|+ε)-1}

(20)

其中αi为第i个单元对应的损伤参数，ε为一正常数，避免因αi→0而导致矩阵对角元素趋于∞。

当L为一般的对角矩阵时，式(15)等价于求解

(CTC+ξ2LTL)α=CTb

(21)

该方程的解为

(22)

由于正则化矩阵L(α)需用损伤参数α来构造，而α为待求的未知量，因此，需要采用迭代的方式进行求解。

需要注意的是，正则化参数ξ的选取是利用正则化方法求解线性不适定问题的关键。前述研究中，学者们一般采用L曲线法选取正则化参数，而L曲线的绘制通常需要进行大量的试算，尤其是对于复杂的大型结构系统。此外，当噪声水平较高时，L曲线趋于平直，很难通过该方法选取合适的正则化参数。为解决正则化参数选取时需要大量试算的问题，提出了一种奇异值二分法用于本文新方法中正则化参数的选取。

基于Tikhonov正则化迭代求解(Tikhonov Regularization Iterative Method，TRIM)的损伤识别过程如下：

步骤1构建损伤检测线性系统，求得系统的初始解

根据结构损伤前后的模态信息利用损伤检测方法(如CMSE)构建方程组Cα=b。对系数矩阵C进行奇异值分解，获得系统的r个奇异值σ1≥σ2≥…≥σr≥0。

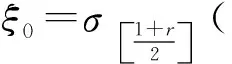
(23)

步骤2调整正则化参数，重构正则化矩阵，进行第k次迭代求解

(1) 基于奇异值二分法调整正则化参数ξ

(24)

相应的正则化参数调整为

(25)

上述选择和调整正则化参数的方法，我们称之为奇异值二分法。

(26)

(27)

此处ε统一取为0.01%，以减小对损伤检测结果的影响。

(3) 进行第k次求解

应用新的迭代参数ξk和矩阵Lk，计算新的解向量

(28)

步骤3重复步骤2所述过程，直到前后两次迭代求解的向量差值满足如下条件

(29)

其中δ为收敛阈值，本文建议δ=0.1%，在保证求解精度的同时，控制所需要的迭代步数。基于新方法的最终损伤识别结果为

(30)

基于Tikhonov正则化迭代求解的CMSE损伤检测(简称CMSE-TRIM)流程如图1所示。

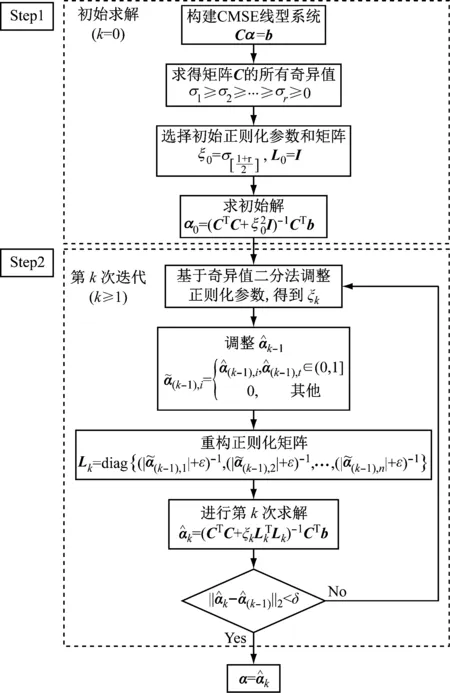
图1 CMSE-TRIM损伤检测流程图

3 数值算例

3.1 海洋平台结构

本算例的研究对象为一个近海导管架平台结构[24]，如图2所示。该结构由36个外径为17.8 cm，壁厚为0.89 cm的均匀钢管构件组成，每根钢管划分为一个单元。结构三层标高分别为9.14 m，18.29 m和27.43 m。底部和顶部的边长分别为10.97 m×10.97 m和3.66 m×3.66 m。平台的四条腿固定于地面。选用材料为钢材，弹性模量2.1×1011Pa，密度7 850 kg/m3，截面面积2.825×10-3m2，截面惯性矩2.89×10-6m4。按照有限元方法组建整体质量矩阵(采用集中质量法)和整体刚度矩阵，进行特征值分析，得到有限元模型的前三阶频率分别为7.51 Hz、8.80 Hz和8.88 Hz。平台前三阶振型如图3所示。

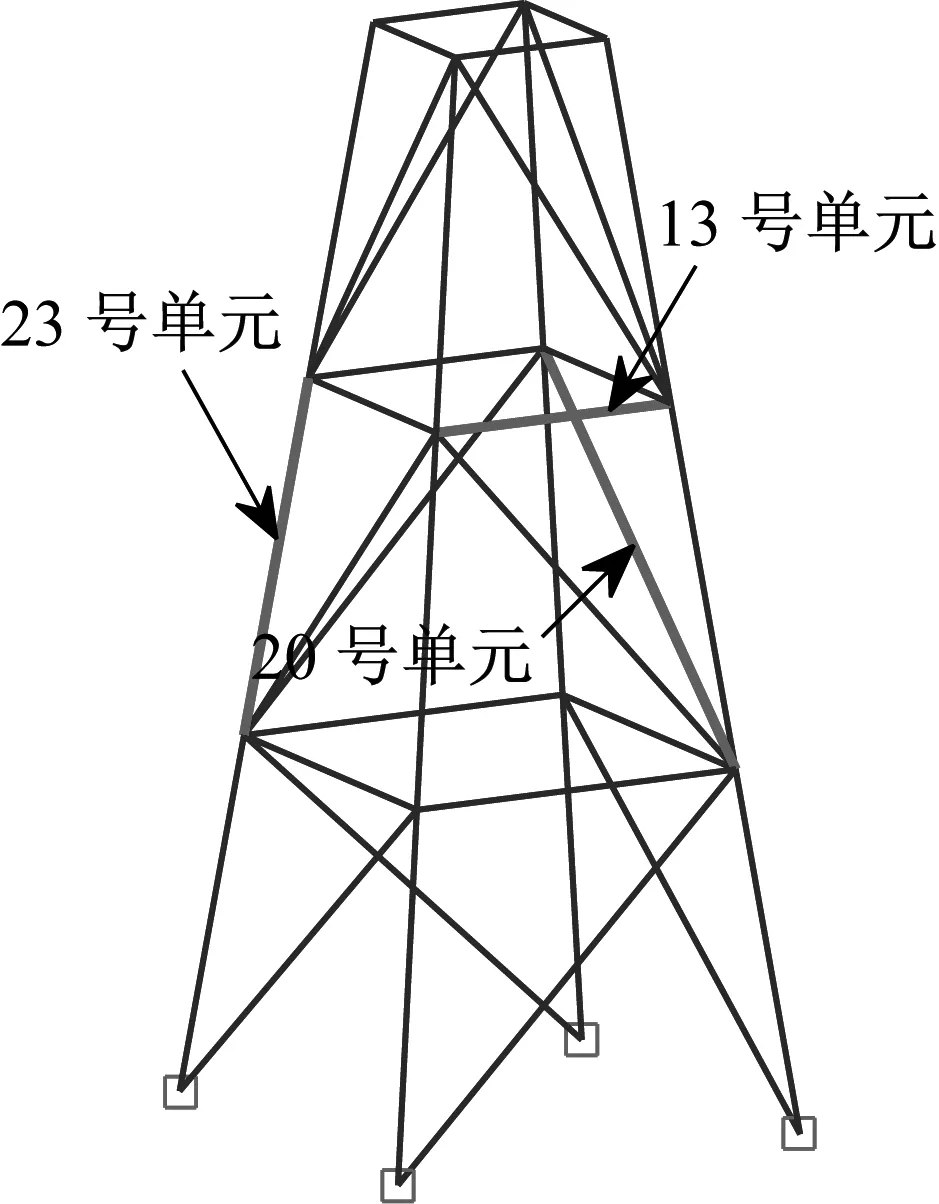
图2 海洋平台结构示意图

图3 有限元模型前三阶振型

3.2 损伤工况设置

由于实际测试中结构的高阶模态一般难以激励，转动自由度信息难以测量，因此本文算例中假设仅能测得损伤结构1～3阶频率以及振型中的平动自由度信息，并且所测振型信息含有一定水平的噪声。

为了研究本文提出的方法在不同因素影响下的损伤识别效果，算例中设置了四类影响因素：① 损伤位置敏感性；② 损伤程度敏感性；③ 噪声水平敏感性；④ 模态阶数敏感性。分别探讨不同影响因素下的损伤识别效果。结构损伤后的振型信息添加一定水平噪声，噪声添加方式如下

φi,j=φi,j(1+μGi,j)

(31)

式中,μ为噪声水平；Gi,j为均值为0、方差为1的高斯随机数；φi,j为对应于第i个自由度的第j阶振型值。实测频率信息一般较为准确，因此算例中不考虑噪声对频率的影响。

4 损伤识别与结果分析

本文采用Guyan扩阶方法对仿真模拟得到的损伤后模态振型进行扩阶处理，利用损伤前后的模态信息构建CMSE方程，求解36个单元(n=36)的损伤参数。并对比CMSE-Tikhonov(基于Tikhonov正则化求解的CMSE损伤检测)和CMSE-TRIM的损伤识别效果。

4.1 损伤位置敏感性

设置噪声水平1%，损伤程度25%，选用结构损伤后1～3阶模态，研究损伤方法对不同类型损伤构件(工况S1：13，工况S2：20，工况S3：23)的损伤识别效果。

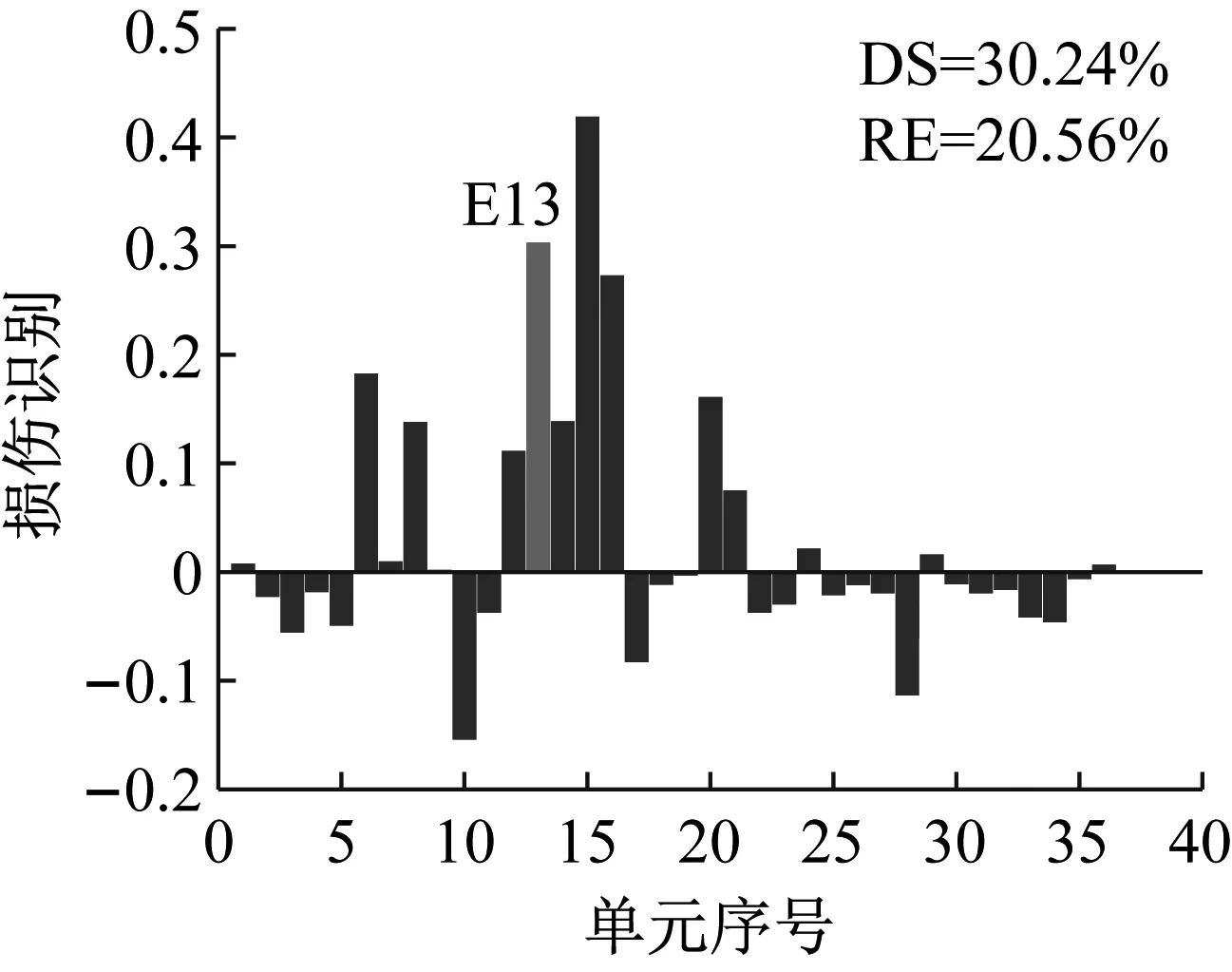
工况S1设置13号单元发生25%损伤，在测量模态空间不完备及1%噪声影响下利用CMSE-Tikhonov方法进行损伤识别，具体求解过程如下：首先根据1.1节内容构建CMSE方程组Cα=b，对系数矩阵C进行奇异值分解，并将得到的所有奇异值分别假设为正则化参数，根据式(16)进行试算并绘制L曲线图(如图4)；找出L曲线最大曲率点所对应的奇异值，作为最终选用的正则化参数，进而求解损伤向量。由L曲线法选取的正则化参数为ξ=7.20×107，根据式(16)进行求解，最终识别结果如图5(a)所示，其中，深灰色表示干扰项，浅灰色表示损伤单元的损伤指标。此外，图中DS(damage severity)，表示实际损伤单元的损伤程度；RE(relative error)，表示评估的损伤程度与真实值的相对误差；c表示迭代的总次数。

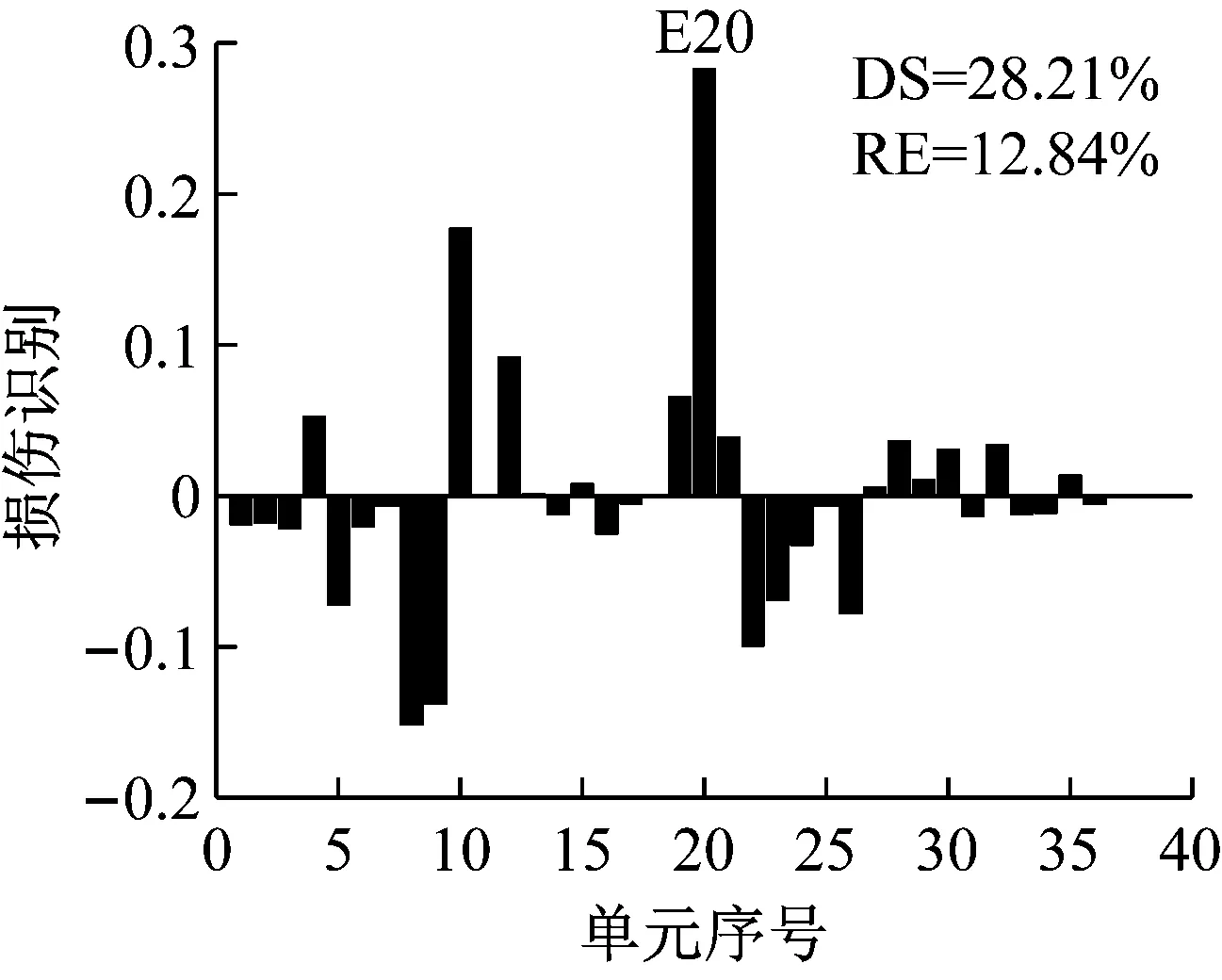
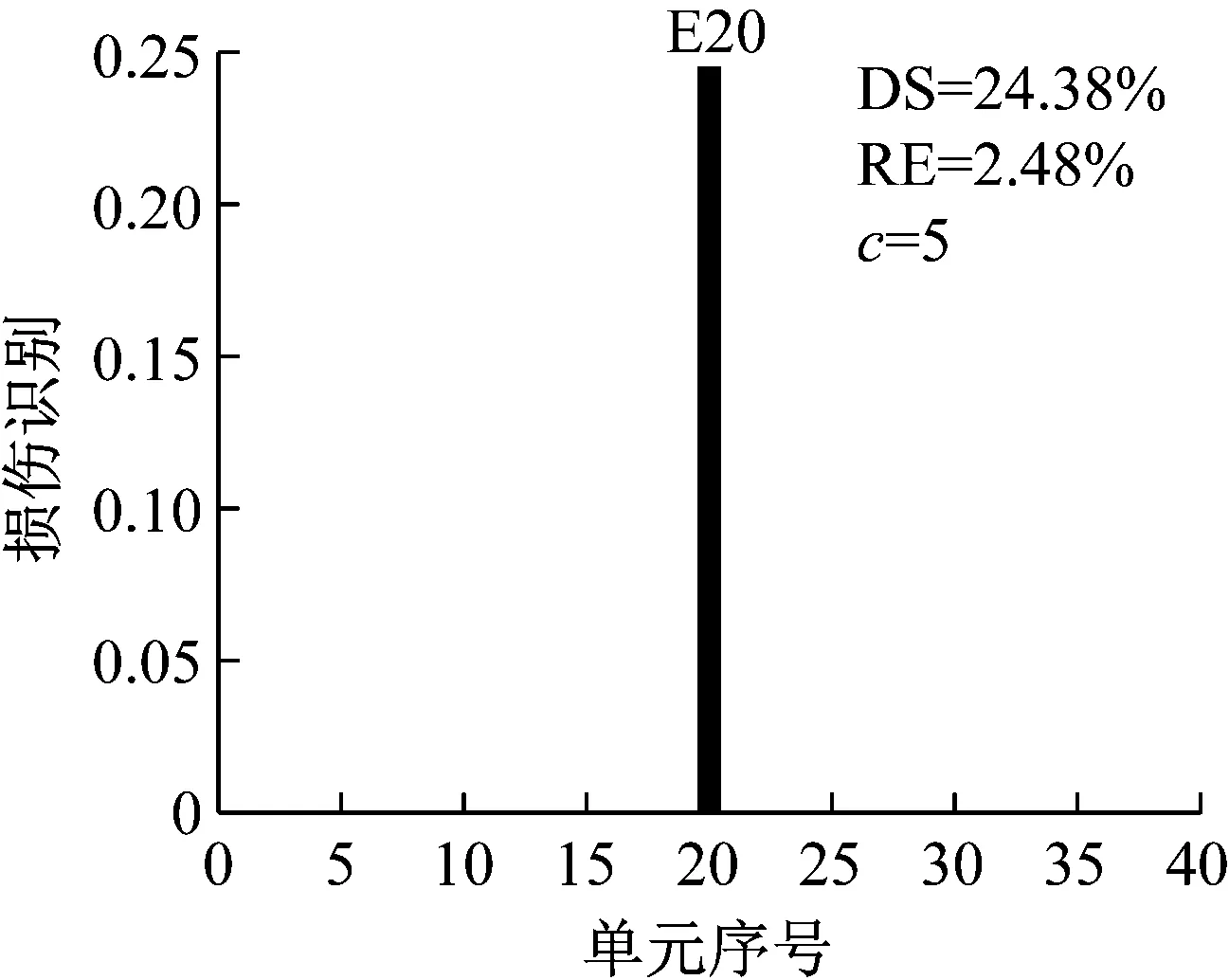
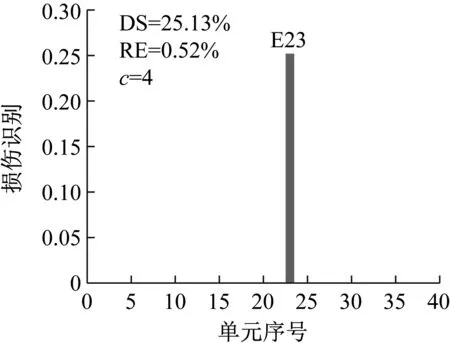
应用CMSE-TRIM对工况A进行损伤识别的过程如下：构建CMSE方程组Cα=b，对矩阵C进行奇异值分解，并直接选取矩阵C的中间奇异值σ18=1.06×108作为初始的正则化参数；按照图1所示流程进行迭代求解，迭代9次后计算结果达到收敛阈值，最终求解结果如图5(b)所示(图中c表示迭代次数)。工况B和工况C损伤识别过程与工况A类似，具体流程不再赘述，最终求解结果分别见图6和图7。应用TRIM方法所得损伤单元各迭代步下的计算结果如图8所示。

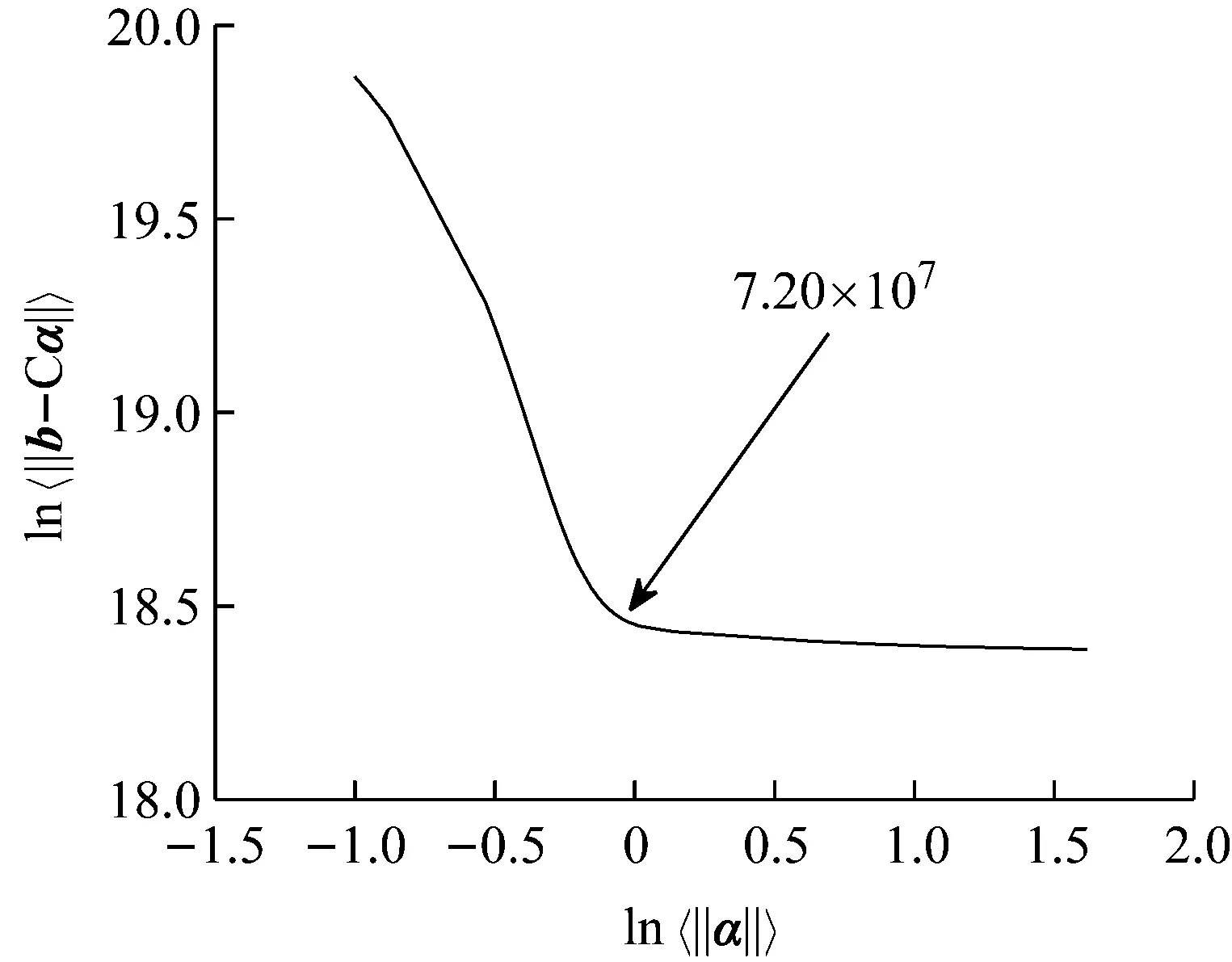
图4 工况S1 “L曲线”图

对比三种不同损伤位置下CMSE-Tikhonov求解结果，可以看出，该方法对立柱单元损伤检测效果最好，斜撑次之，横撑检测效果最差。相比之下，CMSE-TRIM方法对上述三工况的损伤识别结果都非常好，无论是在损伤定位还是损伤程度识别方面都明显优于CMSE-Tikhonov方法。从图8中损伤单元各迭代步计算结果可以看出，13号横撑损伤时迭代次数最多(9次)，20号斜撑次之(5次)，识别23号立柱损伤所需迭代次数最少(4次)。迭代次数的多少侧面反映出不同类型损伤单元的损伤识别难易程度，即相同条件下，立柱损伤最容易识别，斜撑次之，横撑损伤最不易识别。此外，从图8中13号单元迭代结果变化可以看出，该计算结果经历了由大变小，由小变大，最后逐渐趋于稳定这几个阶段，体现出TRIM方法能够自适应调节计算结果的特性。

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

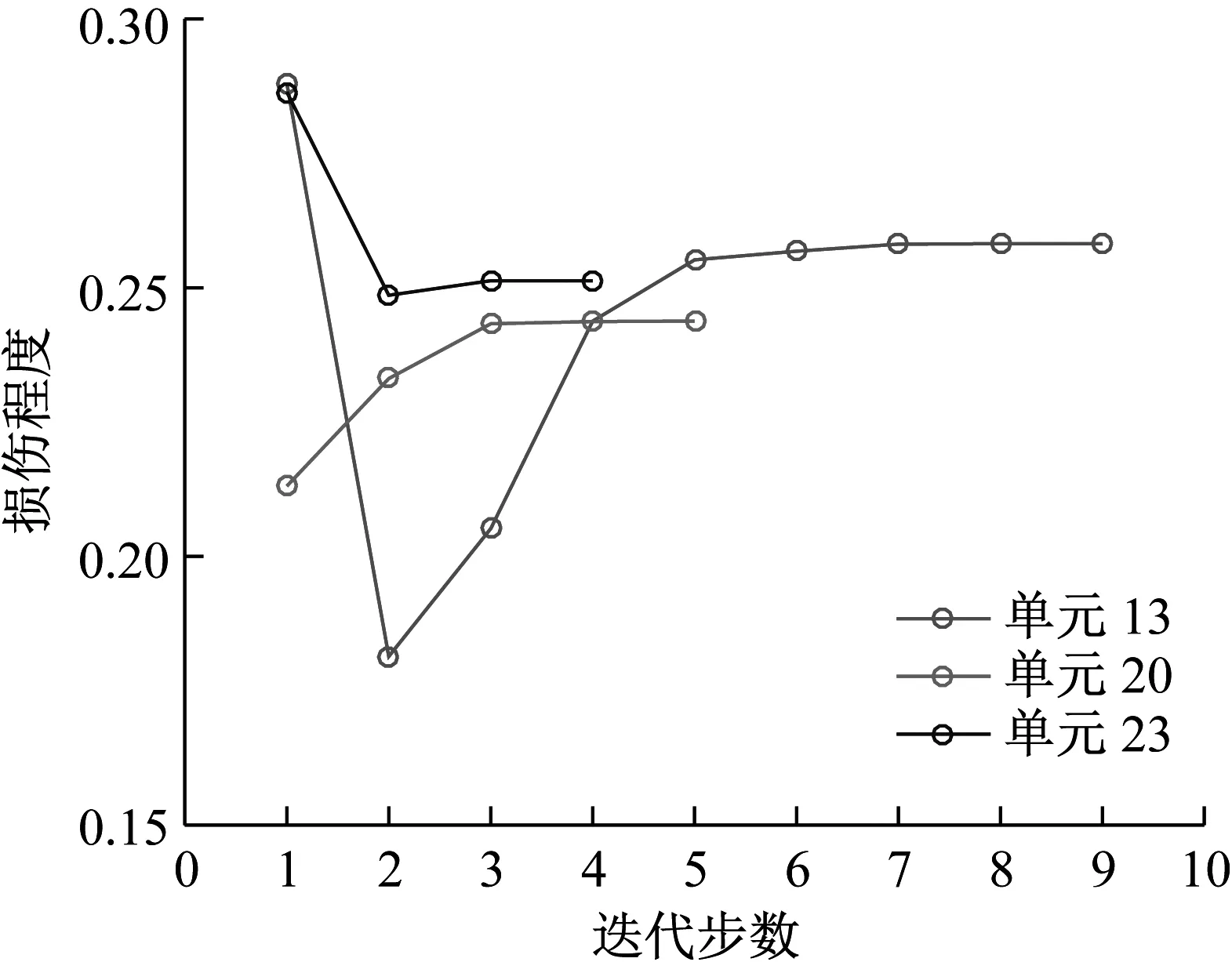
图8 各损伤单元不同迭代步的损伤程度计算结果

4.2 损伤程度敏感性

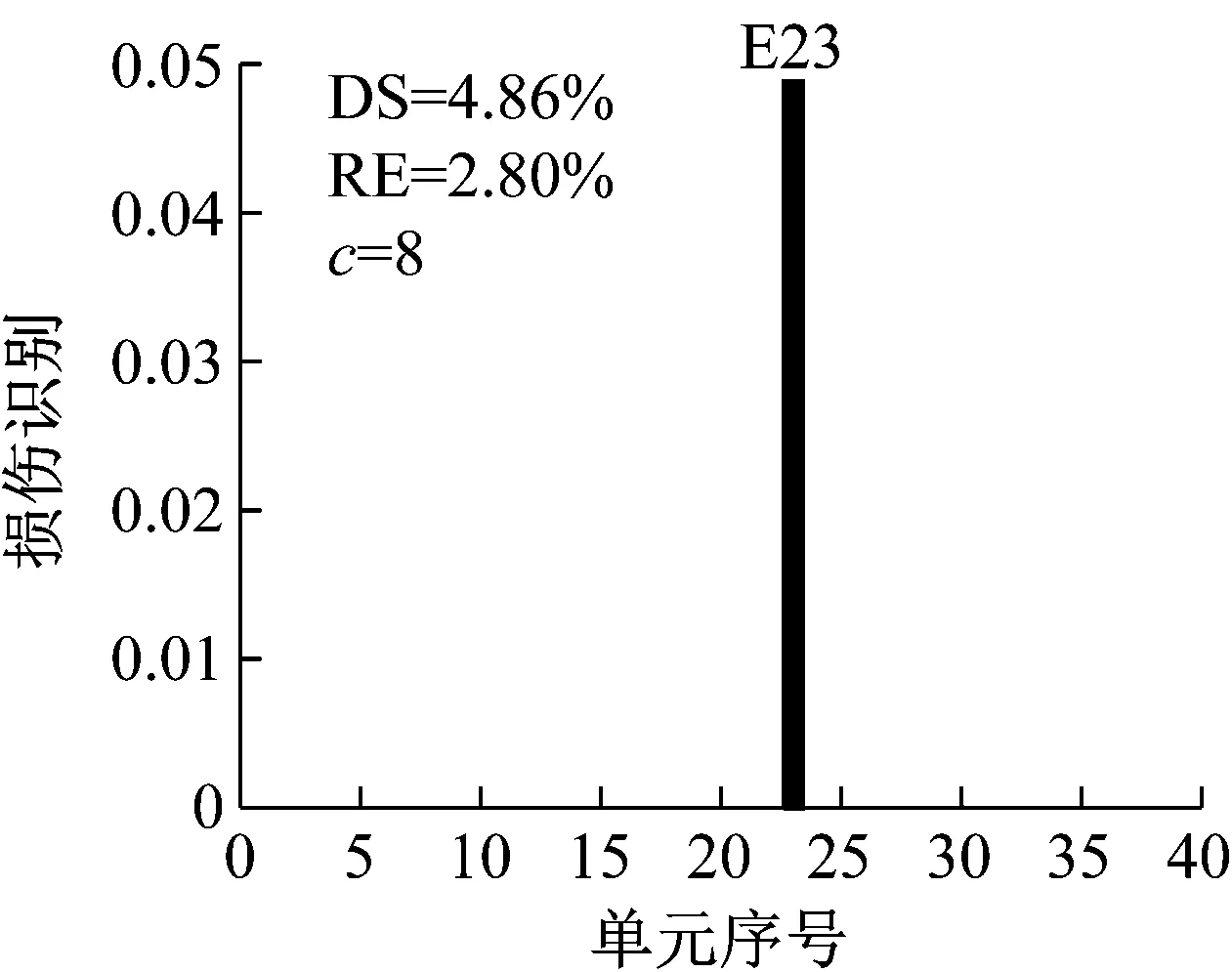
设置噪声水平1%，损伤单元23，选用结构损伤后1～3阶模态，研究损伤方法对不同损伤程度(工况D1：5%，工况D2：15%，工况D3：25%)的损伤识别效果。两种方法识别结果如图9～图11所示。

由图9～图11可以看出，当单元的损伤程度较小时，使用CMSE-Tikhonov方法会出现大量的虚假损伤掩盖真实的损伤信息，从而无法完全损伤检测；随着损伤程度的增加，求解结果中的干扰项逐渐减少，损伤程度识别误差也逐渐减小。相比之下，CMSE-TRIM对三种不同损伤程度的工况均能正确识别出损伤单元的位置，而且没有出现虚假损伤。在损伤程度识别方面，CMSE-TRIM的识别误差明显小于CMSE-Tikhonov方法。此外，从计算所需的迭代次数上可以看出，在其他影响因素相同的条件下，TRIM方法需要较多的迭代次数来计算小损伤工况。

4.3 噪声水平敏感性

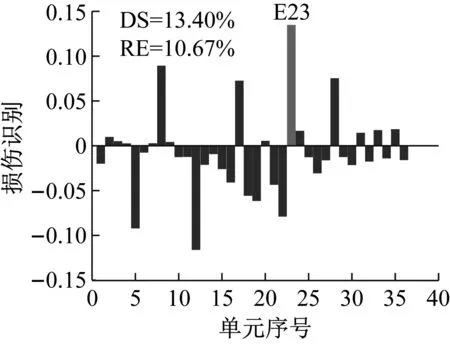
设置损伤单元23，损伤程度25%，选用结构损伤后1～3阶模态，研究损伤方法在不同噪声水平(工况N1：1%，工况N2：3%，工况N3：5%)下的损伤识别效果。识别结果如图12～图14所示。

分析图12～图14可以看出，当噪声水平相对较低时，使用CMSE-Tikhonov方法能够较好地识别出损伤位置及损伤程度，干扰项较少。随着噪声水平的提高，该方法损伤识别效果逐渐变差：在损伤定位方面，虚假损伤干扰项逐渐增多，掩盖了真实的损伤信息；损伤程度识别误差也逐渐增大。与之相比，CMSE-TRIM在不同噪声水平影响下均能正确判定出损伤位置，不掺杂任何虚假损伤，而且损伤程度识别精度明显高于CMSE-Tikhonov。此外，从计算所需的迭代次数上可以看出，在其他影响因素相同的条件下，当影响实测模态的噪声水平提高时，TRIM方法计算所需的迭代次数相应增加。

(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

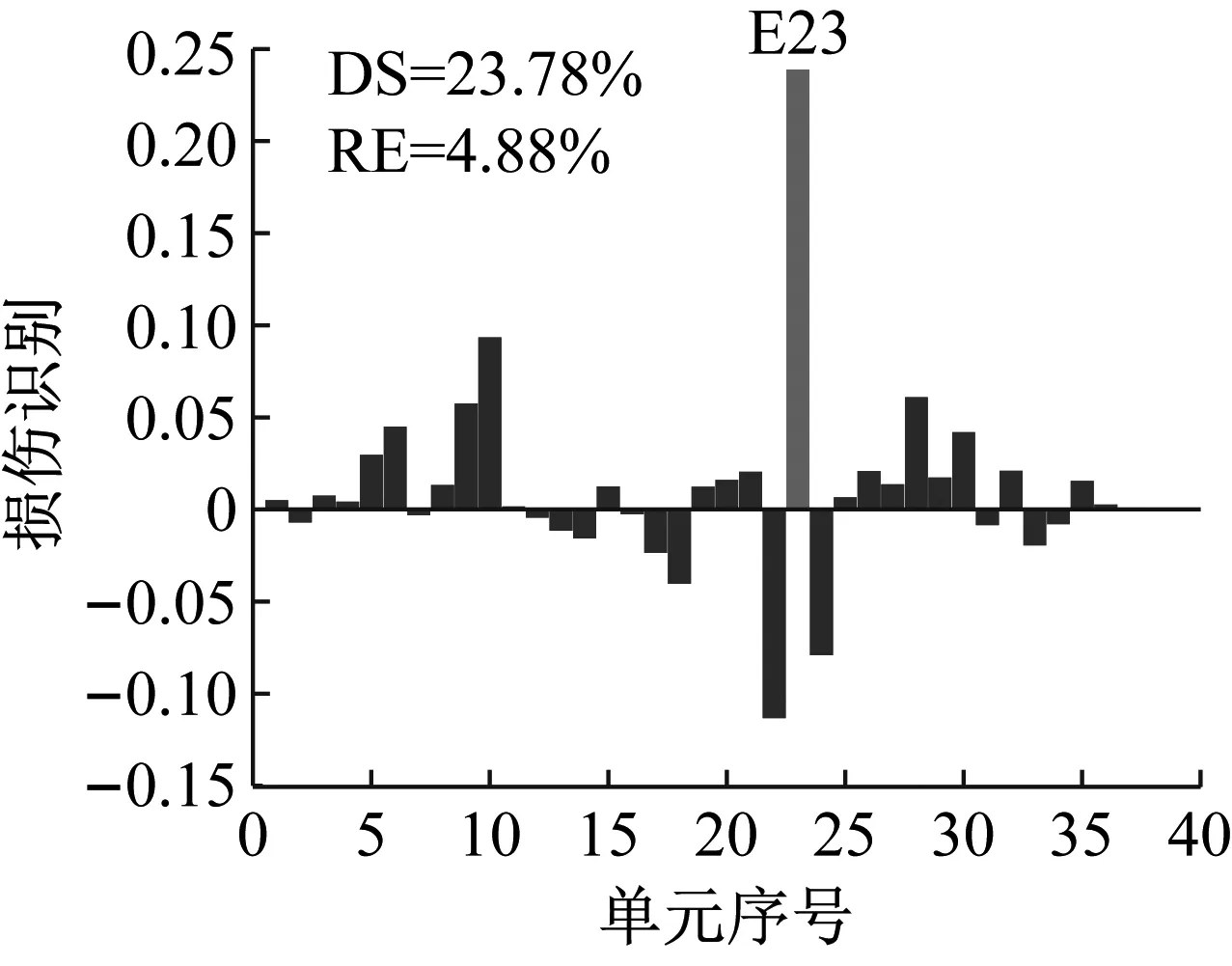
(a) CMSE-Tikhonov

(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

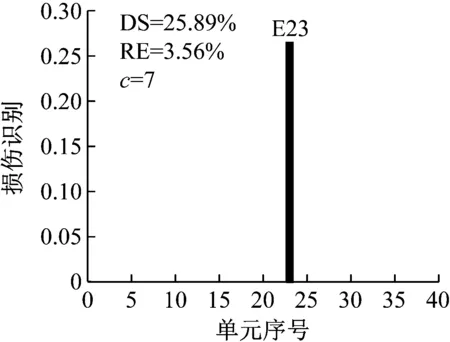
(b) CMSE-TRIM

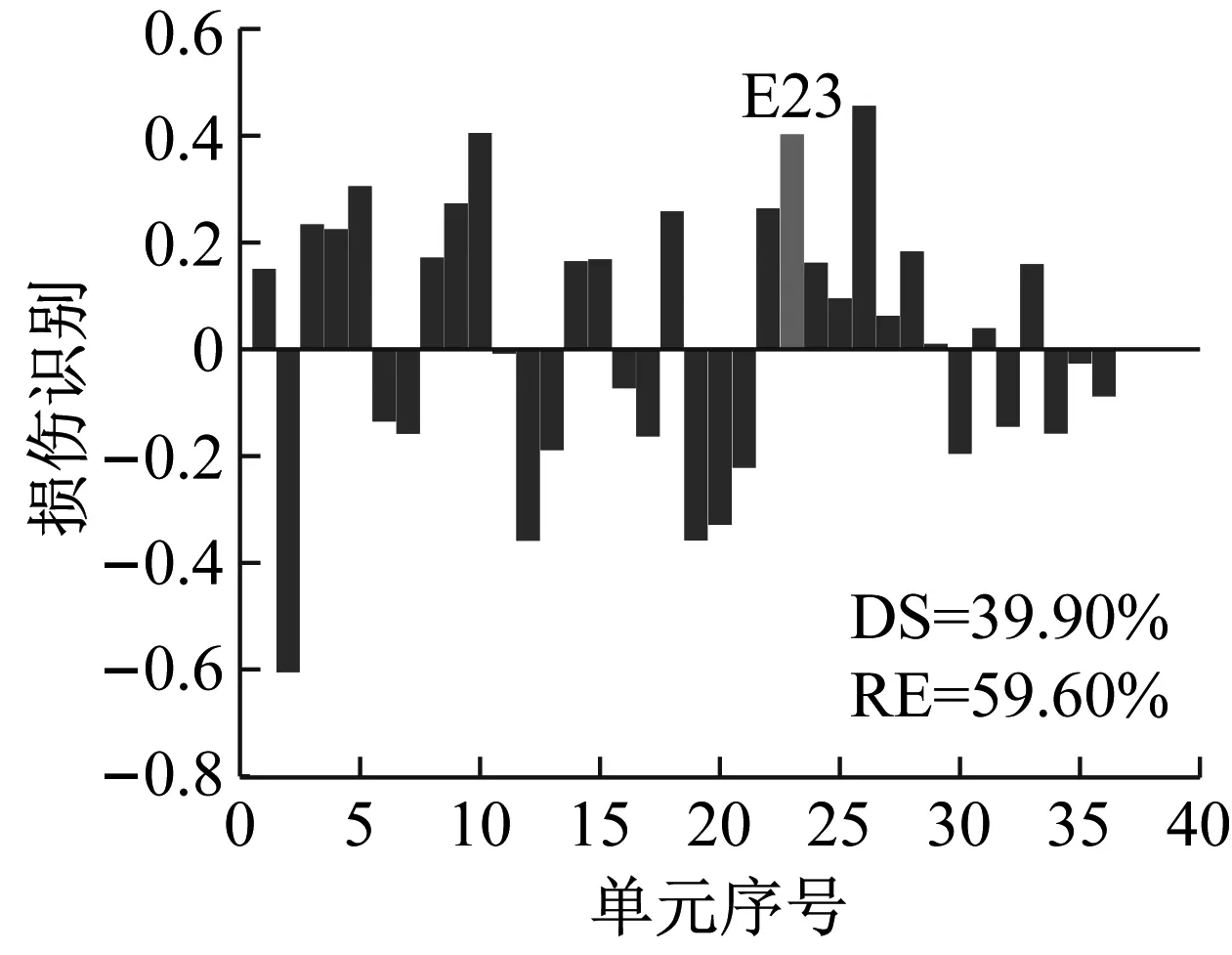
(a) CMSE-Tikhonov

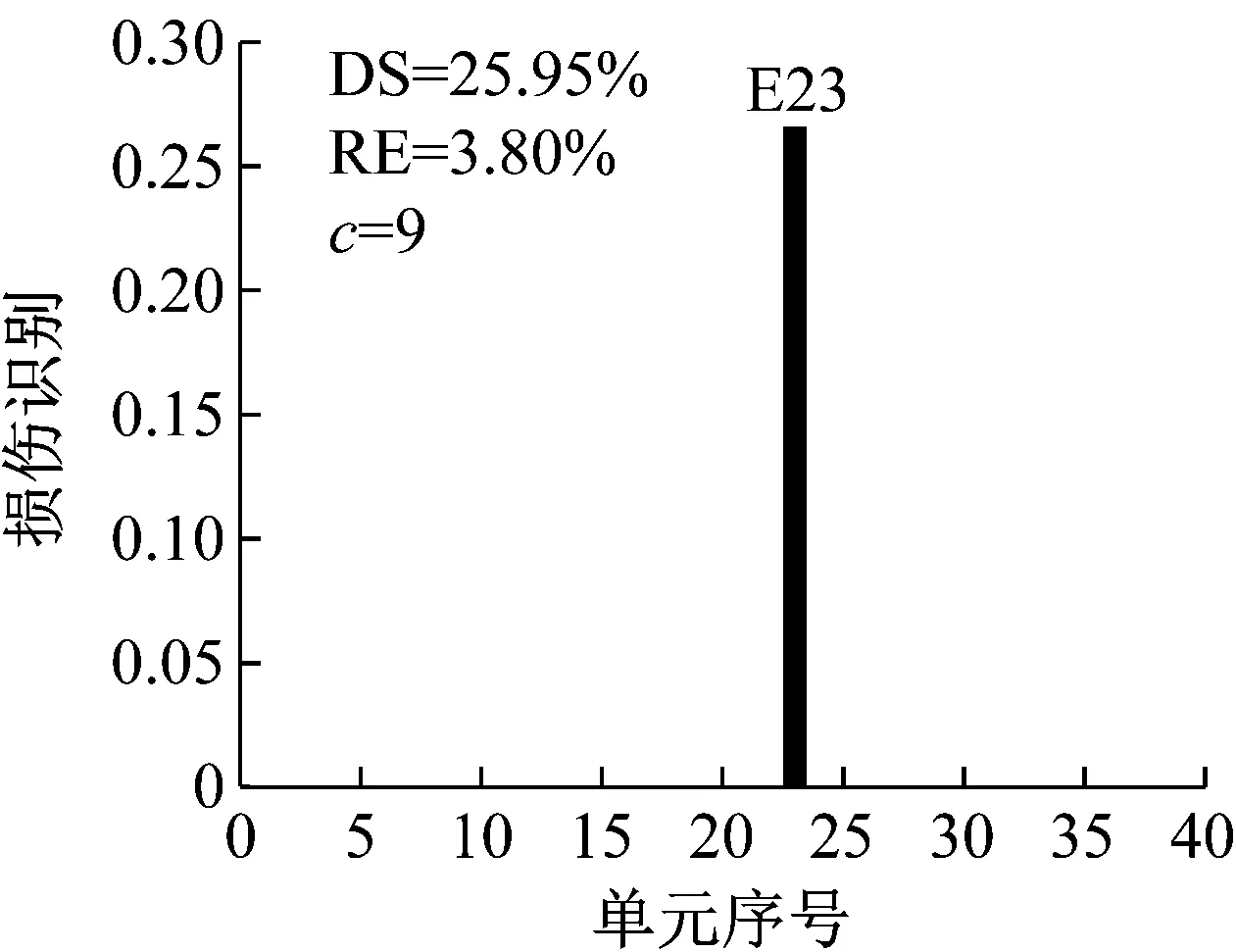
(b) CMSE-TRIM

4.4 模态阶数敏感性

设置噪声水平1%，损伤单元23，损伤程度25%，研究使用结构损伤后不同阶数模态(工况M1：1，工况M2：1～2，工况M3：1～3)的损伤识别效果。两种方法识别结果如图15～图17所示。

从图15～图17可以看出，当取用的损伤后模态只有第1阶时，使用CMSE-Tikhonov和CMSE-TRIM都无法完成损伤识别；当取用的损伤后模态为前2阶时，CMSE-Tikhonov方法虽然能够识别出23号单元发生损伤，但是求解结果中掺杂多处虚假损伤干扰项，损伤程度求解误差为14.20%；当取用的损伤后模态为前3阶时，CMSE-Tikhonov求解结果中干扰项明显减少，损伤程度识别精度有所提高。相比之下，当取用的损伤后模态为前2阶或前3阶时，CMSE-TRIM方法均能正确判定出损伤位置，不掺杂任何虚假损伤，而且损伤程度识别精度明显高于CMSE-Tikhonov。此外，从计算所需的迭代次数上可以看出，在其他影响因素相同的条件下，取用的损伤后模态阶数越多，TRIM方法计算所需的迭代次数越少。

(a) CMSE-Tikhonov

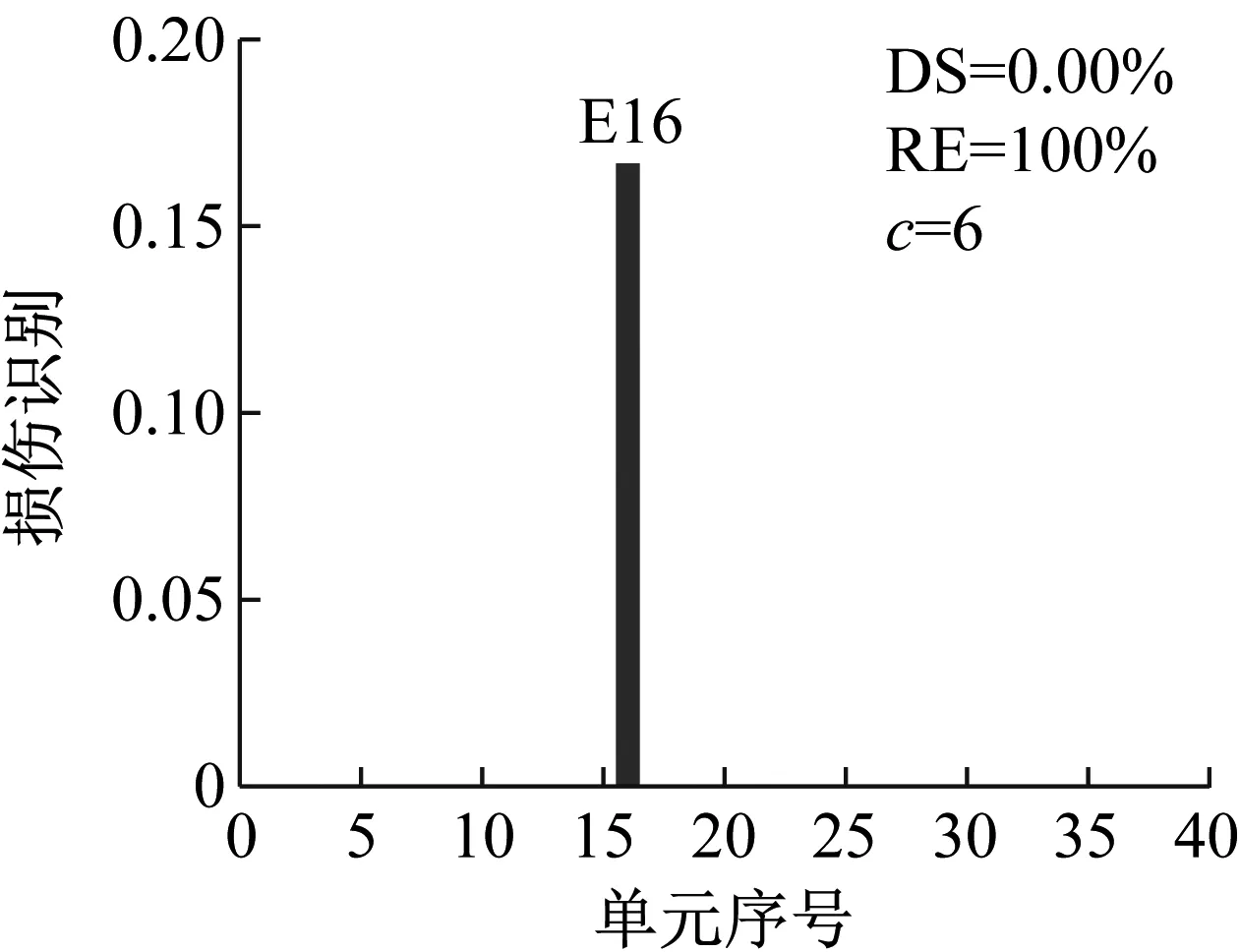
(b) CMSE-TRIM

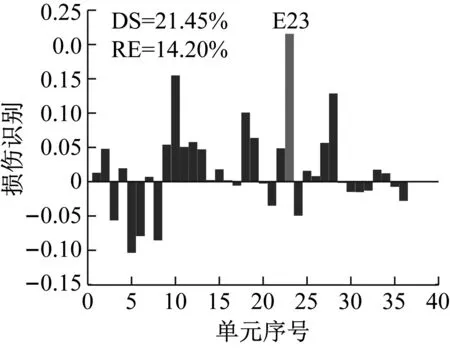
(a) CMSE-Tikhonov

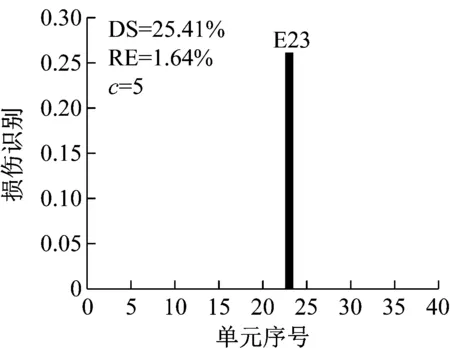
(b) CMSE-TRIM

(a) CMSE-Tikhonov

(b) CMSE-TRIM

5 结 论

针对测量噪声影响下损伤检测“病态”方程组的求解问题进行了研究，提出了一种基于Tikhonov正则化的迭代求解方法来抑制测量噪声对损伤检测的影响。选取一个海洋平台结构开展数值模拟，探讨了新方法在不同因素(损伤位置，损伤程度，噪声水平，取用模态阶数)影响下的损伤识别效果，并同传统Tikhonov正则化求解下的损伤检测进行了对比，结论如下：

传统的Tikhonov正则化方法和本文提出的基于Tikhonov正则化的迭代求解方法均能在一定程度上解决噪声影响下“病态”方程组的求解问题。相对于传统的Tikhonov正则化求解方法，本文方法能够有效地抑制虚假损伤、不遗漏真实损伤，具有更好的噪声鲁棒性。此外，本文方法直接选取方程组系数矩阵的中间奇异值作为初始正则化参数，通过迭代来自适应调整正则化参数及矩阵，无需通过大量试算来绘制L曲线图，减少了计算工作量。数值分析表明，CMSE-TRIM方法对海洋平台结构不同类型及不同损程度的损伤工况均能正确地识别，具有较好的噪声鲁棒性。损伤位置不敏感、损伤程度较小、噪声水平较高以及取用的模态阶数较少都会增加损伤检测的难度，相应地会增加TRIM方法的迭代计算次数。