一种可改善传动稳定性的混合励磁型磁齿轮研究
井立兵, 陈俊霖, 张 廷
(1.三峡大学 电气与新能源学院,湖北 宜昌 443002; 2.湖北省微电网工程技术研究中心(三峡大学),湖北 宜昌 443002)
机械齿轮作为一种主要的传动方式广泛应用于工业生产中,但由于轮齿间相互接触不可避免产生摩擦、噪音、振动等问题,而磁齿轮利用磁场间相互耦合实现转矩传递,较机械齿轮具有无接触、低噪声、无需润滑和自动过载保护等优势[1-3]。
20世纪初美国学者提出了磁齿轮的概念并申请专利,从此开启了磁场传动的先例[4]。由于早期磁齿轮拓扑结构单一、永磁材料性能低、永磁体利用率很低,磁齿轮并未受到太多关注。直到Atallah和Howe提出基于磁场调制原理的同轴式磁齿轮[5],磁齿轮才受到研究人员的重视。此后一段时间内,直线式[6]、聚磁式[7]和轴向式磁齿轮[8]相继问世。众所周知,Halbach阵列具有良好的正弦气隙磁通密度分布和自屏蔽磁化特性。文献[9]中提出了一种Halbach同轴式磁齿轮,通过仿真表明,Halbach阵列能大幅度减少气隙磁通谐波含量,增加输出转矩。文献[10]利用二维全局解析法推导了Halbach阵列同轴磁齿轮的气隙磁场分布,并研究其参数与输出转矩间的关系。文献[11]提出了一种新型双通量调制器同轴磁齿轮,旨在提高永磁体利用率和输出转矩。目前,对于改善气隙磁场、增大磁齿轮转矩密度的研究已有很多,而致力于减少转矩脉动,提高磁齿轮传动稳定性还需进一步研究。
针对磁齿轮气隙磁密谐波畸变率高和传动稳定性差的问题,本文提出了一种改善内层气隙磁密分布的偏心表贴式磁极结构,并在外转子轭部开槽加入励磁电流以降低磁齿轮转矩脉动。利用有限元法对传动比为6.75∶1的传统型、开槽未加电流型和开槽加电流型磁齿轮气隙磁场和转矩脉动进行分析与计算,通过仿真表明,偏心磁极能实现对磁齿轮内层气隙磁密的优化,气隙磁密谐波畸变率明显减小,另外施加励磁电流能使磁齿轮具有更好的传动稳定性。
1 工作原理
图1为开槽加电流型磁齿轮的结构模型,主要包含内转子、调磁环和外转子三部分,调磁环对内、外气隙磁场进行调制,从而实现转矩传递。
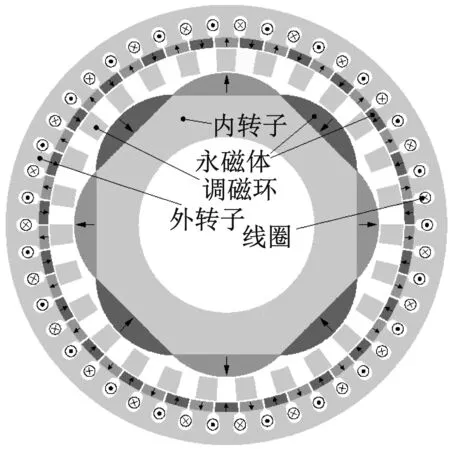
图1 开槽加电流型磁齿轮模型
在不考虑调磁环作用下,气隙内r处的径向磁感应强度可表示为[12]
(1)
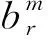
在引入调磁环后,调磁环的径向调制函数可表示为
(2)
由此可得出经调磁环调制后气隙的径向磁感应强度为
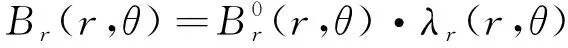
(3)
由文献[13]可知,磁齿轮气隙磁场所含的空间谐波极对数表示为
pm,k=|mp+kns|
(4)
式中:m=1,3,5,…,∞,k=0,±1,±2,…,∞;ns为调磁环的铁心数量。
气隙中的谐波分量具有特定的空间极对数和转速,由文献[14]可知,内、外层气隙空间谐波分量的角速度表示为
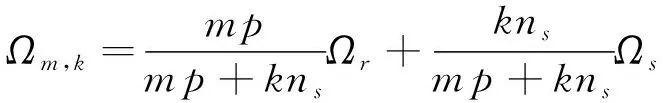
(5)
式中:Ωm,k为空间谐波分量的角速度,Ωr为内、外转子的角速度,Ωs为调磁环的角速度。
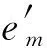

图2 偏心永磁体
2 磁场分析
磁齿轮由内转子、调磁环和外转子三部分组成,内、外转子上均有表贴式磁极,磁极对数按照传动比分配。在本文中外转子上通有励磁电流不便于旋转,因此,以下的研究均指外转子充当定子固定不动,调磁环和内转子旋转,因此传动比指调磁环极对数和内转子极对数之比。另外,本文没有对偏心系数进行深入研究,保证永磁体用量、内层气隙的最短距离和传统型参数相等的情况下,建立传动比为6.75∶1的传统型、开槽未加电流型和开槽加电流型的磁齿轮模型,表1给出了具体的模型参数。

表1 磁齿轮参数
偏心结构的内永磁体使得内层气隙不均匀,外层气隙则为均匀气隙。利用有限元ANSYS Maxwell软件对气隙磁场和电磁转矩进行计算。图3为传统型、开槽未加电流型和开槽加电流型的磁力线分布情况。从磁力线对比图可清晰的看出内转子上有8个波头,这与内转子4对磁极相符。大量的磁力线从调磁环上的导体上穿过,非导体部分上有少量漏磁。开槽未加电流型和开槽加电流型减小部分外层气隙磁场的通路,因此在槽的附近磁路相对易饱和。
图4和图5为三种磁齿轮的内、外层气隙磁密分布图。

(a) 传统型
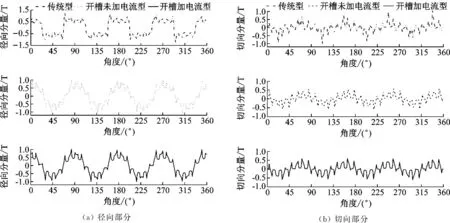
图4 内层气隙中间磁通密度
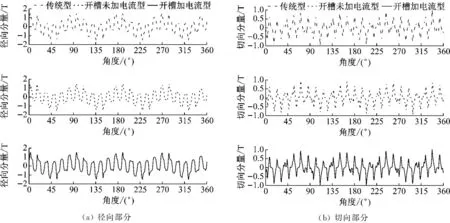
图5 外层气隙中间磁通密度
如图4(a)和4(b)所示,改变内永磁体形状,开槽未加电流型和开槽加电流型的磁齿轮与传统磁齿轮相比,其内层气隙磁密波形由矩形波变为正弦波,但两者磁密径向分量幅值由传统型的1.25 T降到1 T。主要原因是偏心结构的圆弧状磁极改变了内层气隙长度,且由均匀气隙变为不均匀气隙。如图5(a)和5(b)所示,传统型、开槽未加电流型和开槽加电流型三者的外层气隙磁密均没有变化,径向磁密幅值为1.5 T,切向磁密幅值为0.75 T,说明改变内永磁体形状对外层气隙磁密的影响较小。
图6和图7为磁齿轮内、外层气隙磁密经傅里叶分解后的谐波对比图。
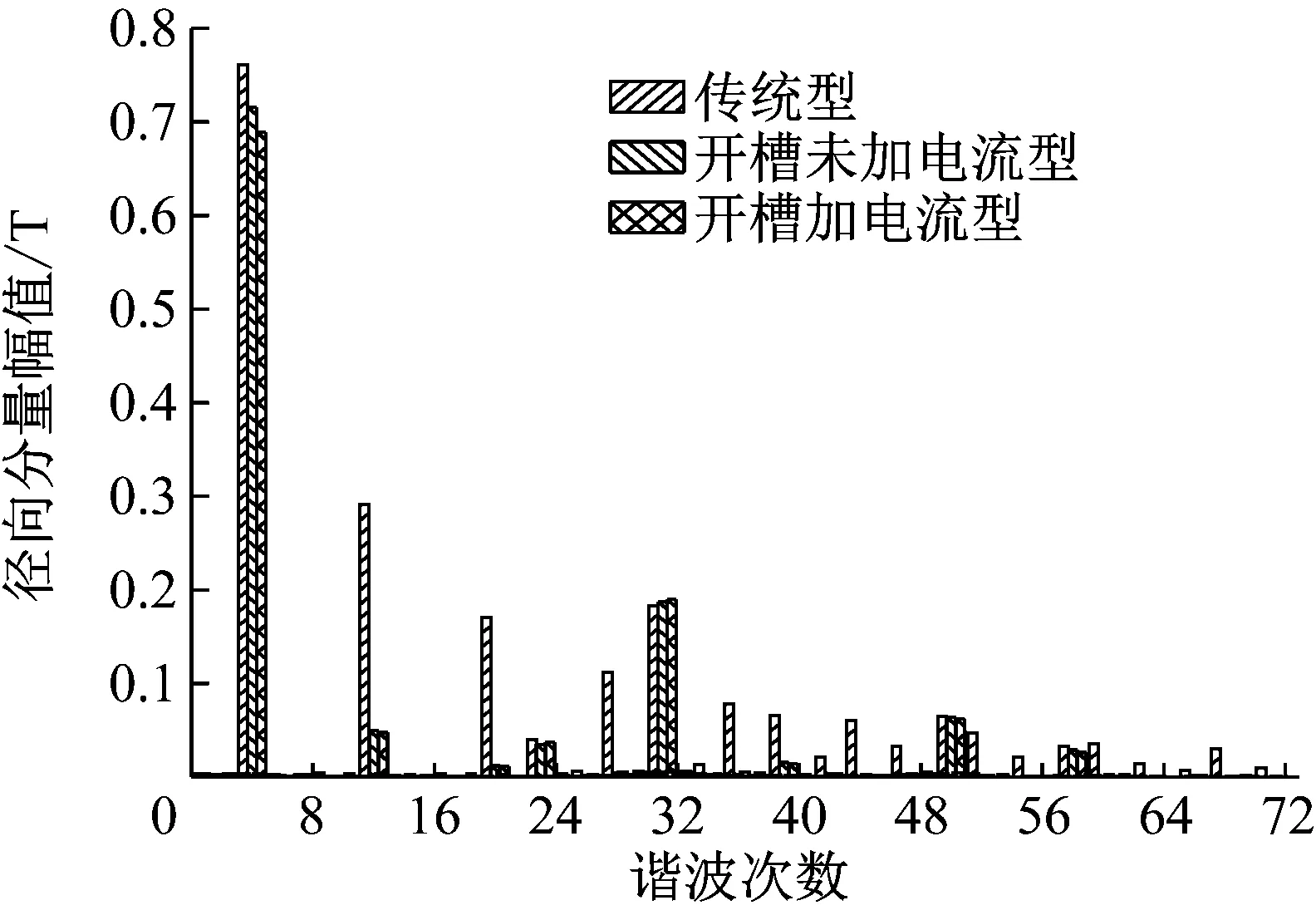
(a) 内层磁密径向分量
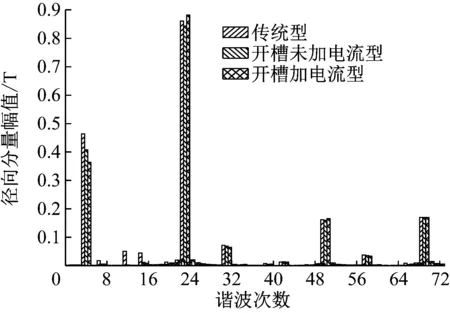
(a) 外层磁密径向分量
如图6(a)和6(b)所示,内层气隙磁密不仅有基波,还有因调磁环的存在而引起的谐波。传统型主要含有4、12、20、23、28、31、36、39、44和50次等谐波;改变内永磁体形状后气隙磁密谐波主要含有4、12、23、31和50次等谐波,相比传统型,消除了20、28、36、39、44和50次等高次谐波,降低了谐波畸变率,有利于提高磁齿轮的传动稳定性。如图7(a)和7(b)所示,传统型、开槽未加电流型和开槽加电流型三者的外层气隙径向谐波含量变化较小;对于外层切向谐波含量,开槽加电流型的4次和31次谐波幅值明显大于另外两者,31次谐波主要是由内永磁体的基波经调磁环调制出来的,说明改变永磁体形状后有利于内、外磁场的耦合,从而增大转矩的输出。
3 电磁转矩计算
静态转矩是衡量磁齿轮性能的重要参数,其值根据麦克斯韦张量法[15-18]可得
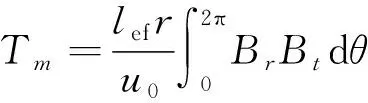
(4)
式中:lef为磁齿轮的轴向长度,Br和Bt为半径为r处的径向和切向磁密分量。
固定外轭铁和调磁环,内转子以675 r/min的速度逆时针转动,从而得到内、外转子静态转矩对比图。如图8所示。
从图8中可看出,内、外转子的静态转矩波形均为正弦波,并且在电角度为90°时达到最大值。从图中看出开槽未加电流型较传统型转矩有所降低,主要是因为外轭铁开槽降低了铁的用量,从而减少了磁力线的回路。开槽加电流型比传统型的转矩更大一些,这是由于电流产生的磁场与永磁体自身磁场叠加增强了外层气隙磁场。传统型、开槽未加电流型和开槽加电流型三者的内转子转矩分别为29.44 N·m、27.35 N·m和29.62 N·m;外转子转矩分别为196.58 N·m、188.23 N·m和199.85 N·m。三者的传动比分别为6.68∶1、6.88∶1和6.75∶1,传统型和开槽未加电流型传动比与理论传动比分别相差1%和1.9%;而开槽加电流型的磁齿轮传动比等于6.75∶1,从而也说明开槽加电流型的磁齿轮传动稳定性更好。
固定外轭铁和外永磁体,令内转子和调磁环分别以675 r/min和100 r/min逆时针旋转,从而得到内、外转子的稳态转矩如图9所示。

(a) 内转子
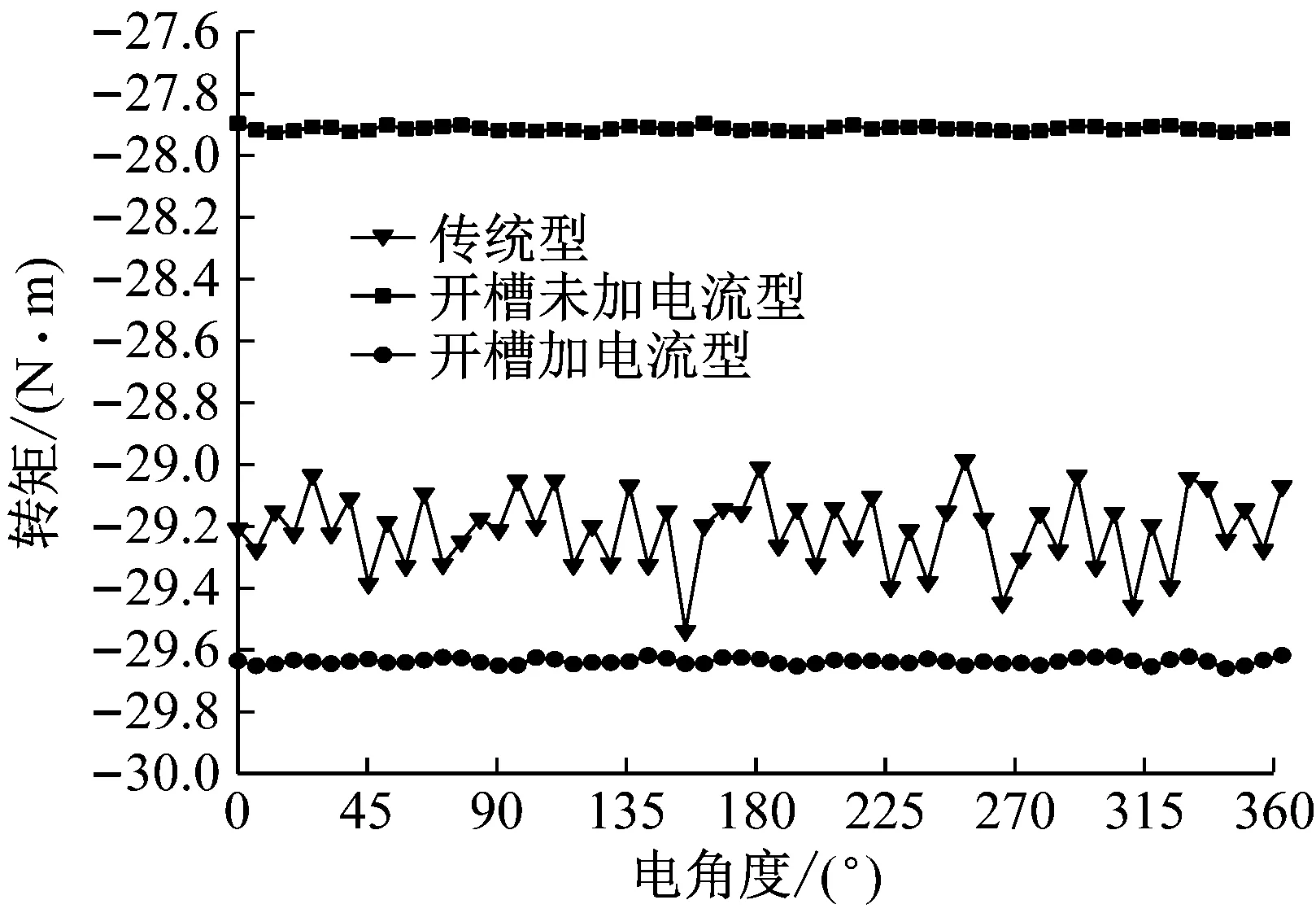
(a) 内转子
从图9中可以看出,传统型的内转子转矩脉动明显大于另外两个模型;而外转子的转矩脉动则更小一些,这是由于外永磁体极对数多于内永磁体极对数。
表2列出了具体的传统型、开槽未加电流型和开槽加电流型的磁齿轮转矩脉动百分比。
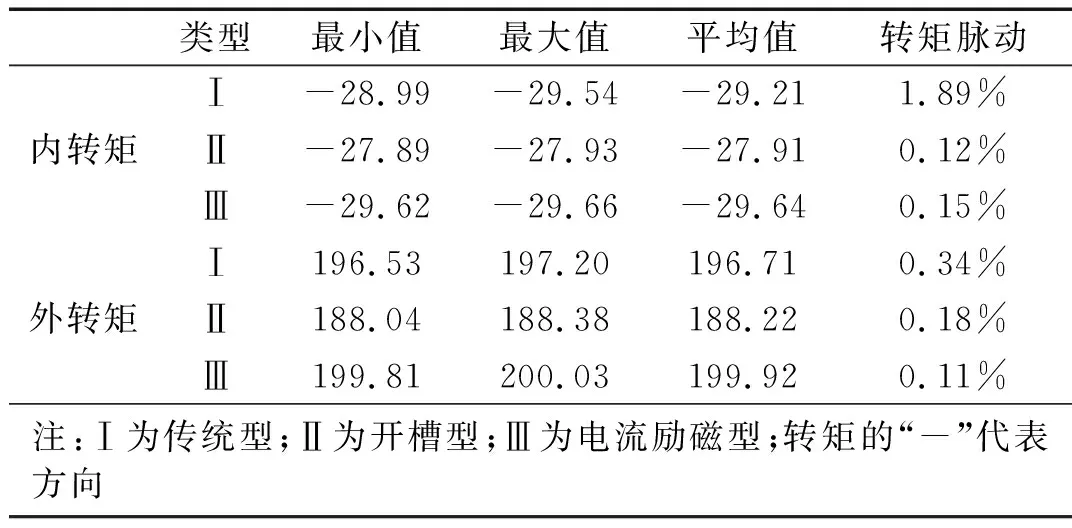
表2 转矩脉动
从表2中可以看出,无论是内转矩还是外转矩,传统型的转矩脉动均大于另外两种,而开槽加电流型的磁齿轮不仅可以提高传动稳定性,相比开槽未加电流型的磁齿轮,也能提高输出转矩。开槽加电流型比传统型的内、外转子输出转矩分别提高了1.46%和1.63%;相对开槽未加电流型,分别提高了6.18%和6.22%。
表3为磁齿轮内层气隙径向谐波畸变率。

表3 气隙谐波畸变率
从表3得知,传统型结构的气隙谐波畸变率最大,为56.97%,开槽加电流型次之,开槽未加电流型的谐波畸变率最小。考虑开槽加电流型较开槽未加电流型转矩提高较多,谐波畸变率相差不大,因此开槽加电流型的磁齿轮较具有良好的转矩性能和较高的传动稳定性。
4 结 论
本文采用二维有限元法计算了传统型、开槽未加电流型和开槽加电流型磁齿轮的磁场分布和电磁转矩。通过比较内、外层气隙磁密、谐波含量、转矩波动发现,偏心永磁体结构有利于改善减内层磁密波形,谐波畸变率较传统型大大降低,提高磁密的正弦度;其次,施加励磁电流不仅能增大磁齿轮的输出转矩,还能降低转矩波动,为改善磁齿轮的传动稳定性提供了一种方法。

