一道三次函数性质问题的拓展探究

广东省广州市执信中学(510080) 朱清波

波利亚在其著作《怎样解题》中曾提到：“问题真正获得解决的评判标准应是我们对原问题的理解比刚开始时更完整和准确”.高考复习备考中，如果教师只注重训练解题的熟练度，课堂气氛会较为沉闷，对学生思维能力上的提升也会相当有限.作为课堂教学的引领者，教师需尽可能选择那些让学生有更深层次理解的例题用于拓展探究，让学生在原有认知的基础上又有新的收获，这是提高课堂复习效率的一个重要手段.本文通过对某地一道一模试题的拓展探究，可以作一个较好的例子来说明以上观点.

问题1已知函数f(x)=x3-x2+ax-a存在极值点x0，且f(x1)=f(x0)，其中x1x0，则x1+2x0=____.

从运算的角度而言本题处理起来并不难，以下是该问题的一个常规解法：

解析由f(x1)=f(x0)，则ax1-a=+ax0-a，化简得由x1x0，故则代入上式后化简得即(x1-x0)(x1+2x0-1)=0，故x1+2x0=1.

解决这个问题若到此为止，就失去了一次探究其更高价值的时机，事实上我们可以启发学生去思考：答案“1”反映了该三次函数的什么性质呢?为此我们可以启发学生先探究一个更一般性的问题.

问题2已知函数f(x)=ax3+bx2+cx+d(a0)存在极值点x0，且f(x1)=f(x0)，其中x1x0，试求出x1和x0的等量关系.

解析由f(x1)=f(x0)，则化简得由x1x0，故又则代入上式后化简得即(x1-x0)(ax1+2ax0+b)=0，故

该推导过程就显示了答案“1”的由来，即问题1是问题2的一种特殊情况，从结果来看这个结论和三次函数的对称中心坐标有一定关系，由f′(x)=3ax2+2bx+c，且这表明三次函数的对称中心为故上述推导可归纳为如下性质：

若函数f(x)=ax3+bx2+cx+d(a0)存在极值点x0，且f(x1)=f(x0)，其中x1x0，记三次函数的对称中心为P(t0,f(t0))，则有x1+2x0=3t0.

我们也可以从图像上来观察该结论，如图1，其几何性质如下：

记P(t0,f(t0))，B(x0,f(x0))，A(x1,f(x1))，过P作AB的垂线，垂足为H，由x1+2x0=3t0，则x1-t0=2(t0-x0)，即AH=2HB.

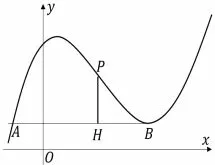
图1

利用上述结论，我们可以重观下面这道高考模拟题：

问题3已知函数f(x)=x3+ax2+bx有两个极值点x1,x2，且x1＜x2，若x1+2x0=3x2，则函数g(x)=f(x)-f(x0)()

A.恰有一个零点 B.恰有两个零点

C.恰有三个零点 D.零点个数不能确定

根据上述结论，不妨设对称中心横坐标为t0，则x1+x2=2t0，而此即表明x0是曲线在点x=x1处切线和图像的另一个交点横坐标，故B选项正确.

是否还有更深入探究方向呢?从图像来看，问题2和问题3均是斜率为0的直线和三次函数图像相切时的位置状态，考虑到相切是两点重合的极限状态，且结论x1+2x0=3t0中两个坐标系数也不一致，我们又可以继续思考，在更一般的情况下，直线和曲线相交(有三个交点)对应的结论又该如何呢?

问题4如图2，已知函数f(x)=ax3+bx2+cx+d(a0)，若方程f(x)=m有三个不相同的实数根x1,x2,x3，则x1+x2+x3=____.

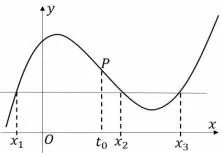
图2

此问题即为考查一元三次方程的韦达定理，我们完全可以采用和二次函数一样的办法来探究这个问题.

解析由题意，可设f(x)-m=a(x-x1)(x-x2)(x-x3)(a0)，又f(x)=ax3+bx2+cx+d，对比函数表达式中x2的系数，有b=-a(x1+x2+x3)，故(或表述为x1+x2+x3=3t0，其中t0是三次函数图像的对称中心横坐标)

这样问题2又变成了问题3的一个特殊情况，问题2即可认为x2=x3时直线和曲线处于相切状态，当然会有

从以上的推导过程来看，我们还会发现三次函数表达式中一次项和常数项并未参与到运算中来，那我们就可以继续探究，如果是一条“斜线”和三次曲线相交，情况又如何?

问题5已知函数f(x)=ax3+bx2+cx+d(a0)，g(x)=mx+n(m0)，若方程f(x)=g(x)有三个不相同的实数根x1,x2,x3，则x1+x2+x3=____.

解析由题意，可设f(x)-g(x)=a(x-x1)(x-x2)(x-x3)(a0)，又f(x)-g(x)=ax3+bx2+(c-m)x+d-n，对比函数表达式中x2的系数，有b=-a(x1+x2+x3)，故

上述推导说明“斜线”是不会改变相关结论的，当然，问题4中若“斜线”与三次函数的图像相切，即x1,x2,x3中有两个根相等，不妨设x2=x3，则结论必然还是利用这个结论，我们就可以探究三次曲线的一般切线问题.

问题6已知曲线y=ax3+bx2+cx+d(a0)，P(x0,y0)是该曲线上一点，试求过P且与曲线相切的直线方程.

解析如图3，分情况讨论.若P是切点，设切线斜率为k1，则此时切线方程为y-y0=k1(x-x0);若P不是切点，设切点为P′(x1,y1)，切线斜率为k2，则故切线方程为y-y0=k2(x-x0).再利用问题4中结论即最后用x0表示k2即可.

图3

在问题5中，我们注意到P作为切点时直线和三次曲线实际上还有一个“较远”的交点，而作为非切点时，另一个切点距离P“较近”，这启发我们可以探究一系列切点的分布规律，从而带来下一个问题.

问题7如图4，已知曲线C:y=ax3+bx2+cx+d(a0)，P0(x0,y0)是曲线C上一点，过P0作C的切线l1，记切点为P1(x1,y1)(x1x0);再过P1作C的切线l2，记切点为P2(x2,y2)(x1x2);······，记第n次操作后切点为Pn(xn,yn)，求

图4

解析利用问题5结论，第n次操作后2xn+xn-1=则令xn-λxn-1=k(xn-1-λxn-2)，对比可得解得或利用第一组解得xn-则

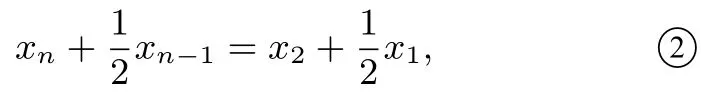
①②式加减消元后得

此结论表明，切点Pn“反复摆动最终会停留”在三次曲线的对称中心处.

利用同样的思考方式，我们还可以启发学生去探究若三次函数图像和二次函数的图像相交，上述结论还成立与否?一元四次函数图像和直线相交会有什么类似的结论等，把这道题的价值挖掘得淋漓尽致.

通过问题1到问题7的推导，我们先将三次函数表达式一般化进而将其与直线的位置关系一般化，再利用一般化的结论去研究另一些特殊位置的性质，逐步探究出这类三次函数问题的本原.日常解题训练中，我们若能启发学生对某些问题答案的合理性和结构规律进行再思考和合理猜想，把它从一个单一的问题求解转换成更一般性问题的性质探索，这种探究活动能让学生真正理解问题的本质特征和逐步培养自身做一道题会一类题的能力，同时该探究过程也会让我们深刻感受数学独特的规律之美.