圆锥曲线多线段长度综合试题及其解法

甘肃省武威第八中学(733000) 王春梅

湖北省阳新县高级中学(435200) 邹生书

以直线与圆锥曲线位置关系为载体的解析几何综合题，位处压轴区分度高具有很好的选拔功能.其中有一类试题条件或所求涉及多条线段的长度关系，这些线段有的是一直线与两曲线构成，有的是两直线与一曲线甚至两曲线所形成，因此问题综合性强难度大.重点考查一元二次方程根与系数的关系，对运算求解以及解答综合问题能力的要较高，大多考生望而生畏而不得不选择放弃.本文笔者试图通过近几年的高考题、竞赛题和最新高考模拟题为例，以线段的构成情况从简单到复杂进行分类诠释这类问题的解法，希望对读者有所帮助.

这些问题都涉及到同一直线上两点间的距离和曲线上弦长的计算，在解题时为了避免重复和提高解题效率我们提炼出了如下两组公式.

第一组公式

(2)若x1,x2是方程ax2+bx+c=0的两个不等实根，则

(3)若P,Q是直线y=kx+b上与对称轴平行于坐标轴的圆锥曲线的两个交点，且由两方程消去y后得到的一元二次方程为px2+qx+r=0，则

第二组公式

(2)若P,Q是直线x=my+n与对称轴平行于坐标轴的圆锥曲线的两个交点，且由两方程消去x后得到的一元二次方程为py2+qy+r=0，则

在解决多线段长度问题时运用上述公式可简化运算缩短解题长度达到事半功倍的作用.

1.一直线与一曲线构成的多线段问题

例1(2017年内蒙自治区高中数学联赛预赛题)过抛物线y2=2px(p＞0)的焦点F作弦BC，若BC的中垂线交BC于点M，交x轴于点N，求证：|MN|2=|FC||FB|.

证明设直线BC的方程为将其代入y2=2px整理得y2-2mpy-p2=0，则B,C两点的纵坐标yB,yC是这个方程的两个根，由根与系数关系得yB+yC=2mp,yByC=-p2.因为点M是BC的中点，所以代入得因为直线BC的斜率为MN⊥BC，所以直线MN的斜率为-m，其方程为令y=0得由点线距离公式得点N到直线BC的距离由焦半径公式得所以

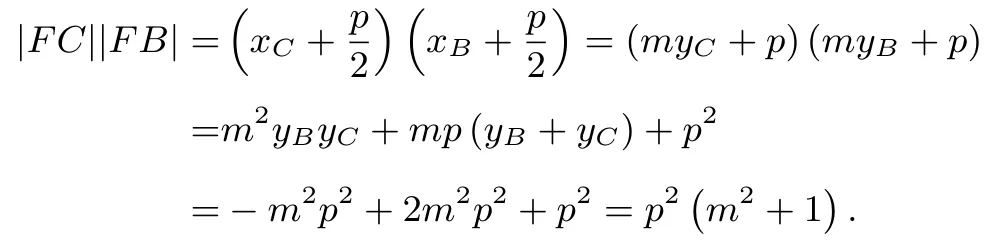
由上可得|MN|2=|FC||FB|.

例2(2016年高考四川卷理科第20题)已知椭圆的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l:y=-x+3与椭圆E有且只有一个公共点T.

(I)求椭圆E的方程及点T的坐标;

(II)设O是坐标原点，直线l′平行于OT，与椭圆E交于不同的两点A,B，且与直线l交于点P.证明：存在常数λ，使得|PT|2=λ|PA|·|PB|，并求λ的值.

解(I)椭圆E的方程为点T的坐标为(2,1)(过程略).

(II)如图1，由(I)知点T的坐标为(2,1)，所以直线OT的斜率为又直线l′平行于OT，故可设直线l′的方程为由直线l′与椭圆E交于不同的两点A,B，知m0.易求得直线l与l′的交点由两点间的距离公式可得将代入椭圆方程整理得3x2+4mx+4m2-12=0，则因为|PA|=所以

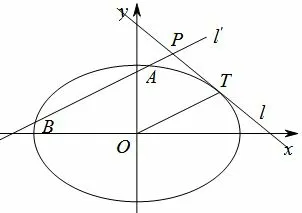
图1

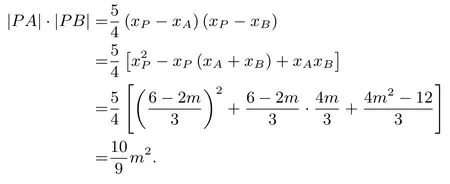
由|PT|2=λ|PA|·|PB|，得所以故存在常数使得|PT|2=λ|PA|·|PB|.

例3在直角坐标系中，以原点为极点，x轴的正半轴为极轴建立极坐标系，已知曲线C:ρsin2θ=acosθ(a＞0).过点P(-1,-2)的直线l的参数方程为

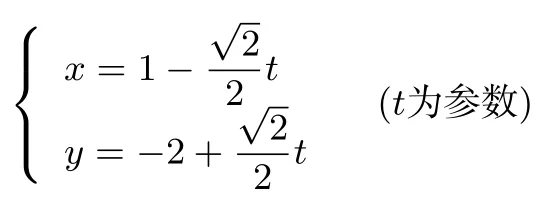
直线l与曲线C分别交于M,N两点.

(1)写出曲线C的直角坐标方程和直线l的普通方程;

(2)若|PM|,|MN|,|PN|成等比数列，求a的值.

解(1)曲线C的直角坐标方程为y2=ax(a＞0)，直线l的普通方程为y=x-1.

(2)法1把y=x-1代入y2=ax得x2-(a+2)x+1=0，则Δ=a2+4a，且xM,xN是这个方程的两个根，由根与系数关系得xM+xN=a+2,xMxN=1.因为|PM|,|MN|,|PN|成等比数列，所以|PM||PN|=|MN|2.又所以

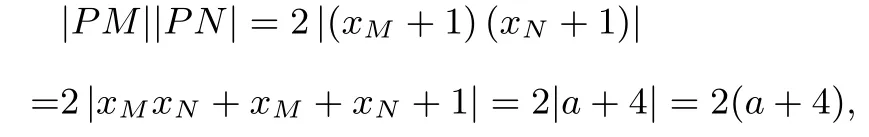
又

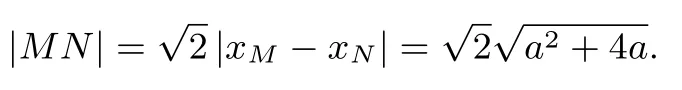
于是有a+4=a2+4a，因为a＞0，解得a=1.

法2由直线的参数方程知直线l过点P且参数t的系数平方和为1，故方程为直线参数方程的标准形式.设点M,N所对应的参数分别为tM,tN，则|PM|=|tM|，|PN|=|tN|，|MN|=|tM-tN|.将直线的参数方程代入y2=ax，得则Δ=2(a2+4a)，且tM,tN是这个方程的两个根，由根与系数关系得因为|PM|,|MN|,|PN|成等比数列，所以|PM||PN|=|MN|2，即|tMtN|=|tM-tN|2，于是有2(a+4)=2(a2+4a)，即(a+4)(a-1)=0，因为a＞0，所以a=1.

2.一直线与二曲线构成的多线段问题

例4(2018湖北八市高三3月联考理科第20题)如图2，已知抛物线x2=2py(p＞0)，其焦点到准线的距离为2，圆S:x2+y2-py=0，直线与圆和抛物线自左至右顺次交于四点A,B,C,D.

(1)若线段AB,BC,CD的长度按此顺序成等差数列，求正数k的值;

(2)若直线l1过抛物线焦点且垂直于直线l，l1与抛物线交于点M,N，设MN,AD的中点分别为P,Q，求证：直线PQ过定点.

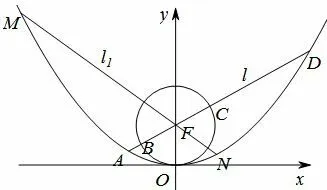
图2

解(1)依题意得p=2，则抛物线x2=4y，圆S:x2+y2-2y=0，直线l:y=kx+1.如图2，因为线段AB,BC,CD的长度成等差数列，所以AB+CD=2B C，则有化简得

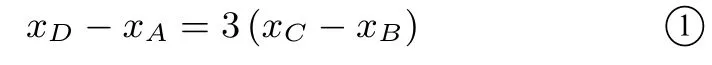
把y=kx+1代入x2=4y得x2-4ky-4=0，Δ=16(k2+1)，所以

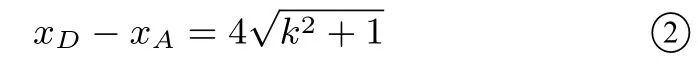
把y=kx+1代入x2+y2-2y=0得(k2+1)x2=1，解得所以

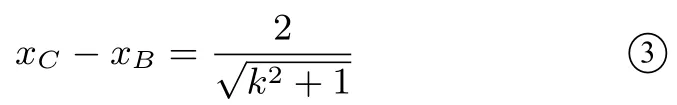
例5(长春市普通高中2018届高三质量检测理科第22题)已知曲线C1的参数方程为(θ为参数).以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρsin2θ=4cosθ.

(1)求曲线C1的普通方程和曲线C2的直角坐标方程;

(2)若过点F(1,0)的直线l与C1交于A,B两点，与C2相交于M,N两点，求的取值范围.

解(1)求得曲线C1的普通方程为曲线C2的直角坐标方程为y2=4x(过程略).

(2)法1设直线l的普通方程为x=my+1，将其代入椭圆方程整理得则yA,yB是这个方程的两个根，由根与系数关系得又|FA|=|yA|,|FB|=|yB|，所以将x=my+1代入y2=4x整理得y2-4my-4=0，则yM,yN是这个方程的两个根，所以有yMyN=-4.又|FM|=|yM|，|FN|=|yN|，所以|FM||FN|=4.于是

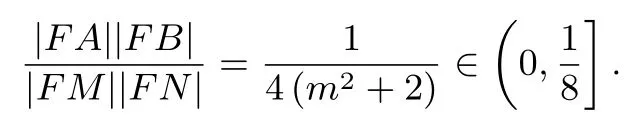
法2设直线l的参数方程为其中t为参数，α为直线的倾斜角，依题意α0.将直线l的参数方程代入整理得2tcosα-1=0.设点A,B所对应的参数分别为tA,tB，则且|FA|=|tA|，|FB|=|tB|，所以将直线l的参数方程代入y2=4x整理得t2sin2α-4tcosα-4=0.设点M,N所对应的参数分别为tM,tN，同理可得于是

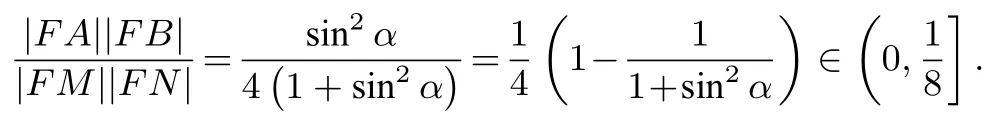
例6如图3，已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A,B两点.

(1)设抛物线在A,B处的切线的交点为M，求证：点M在定直线上;

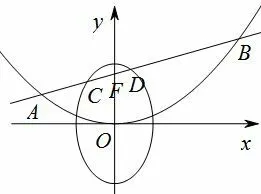
图3

解(1)点M在直线y=-1上(过程略).

(2)由题意知直线l斜率存在设其方程y=kx+1.

当k=0时，直线l平行于x轴，由对称性知等式|AF‖CF|=|BF||DF|显然成立.

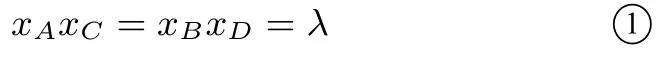
把y=kx+1代入x2=4y得x2-4ky-4=0，则

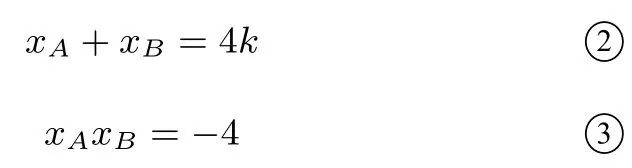
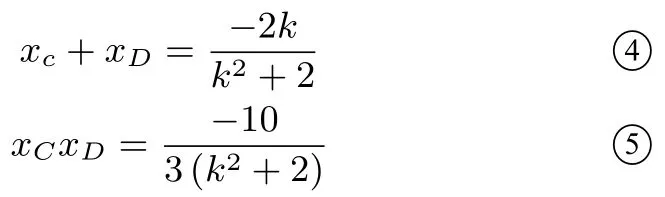
②⑤两式相乘得

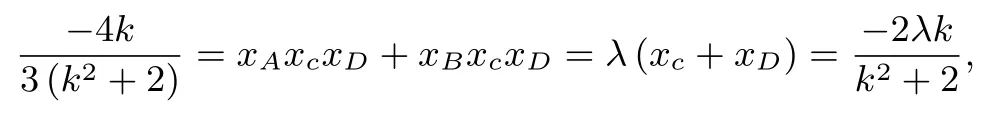
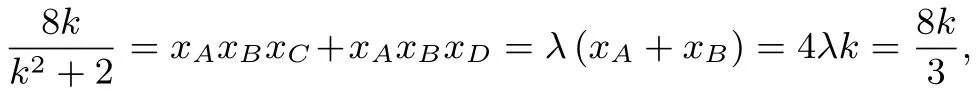
解得k=±1.

综上可知，存在这样的直线l，使|AF||CF|=|BF||DF|，其直线l的方程为y=1，或y=x+1，或y=-x+1.

在解决然数学问题时灵活运用数学公式、定理性质，可以起到简化运算缩小解题长度使问题化繁为简、化难为易达事半功倍之效.在解题中当一些方法或步骤被反复使用时，我们应该有意识对它们进行概括归纳提炼出程序化的或规律性的东西如公式定理性质等，并将其纳入我们的知识结构和思想方法的系统中，同时在今后的解题中遇到类似的问题时积极地加以运用，这样日积月累对我们丰富知识经验提高解题能力都是大有裨益的.