应对平面向量问题的“四化”策略*

江苏省南京师范大学附属扬子中学(210048) 张朋举

平面向量是沟通代数、几何与三角函数的一种重要工具，是高中数学的主干知识之一，在高考中占据着重要的地位.纵观近几年的江苏模考、高考试题，可以看出，平面向量的相关问题的考查难度和力度都有所增加;然而，与此相对的是平面向量题的解法灵活多样、变化多端，在不同问题或同一问题的解决中会产生不同的视角和方法，让学生面对向量问题经常陷入“选择”的困境，要么策略的选择不明确，要么策略使用不灵活.本文以近几年的高考或模考题为例，谈谈应对向量问题时，基底化、坐标化、数量化、图形化等四种策略的合理选择，以期提升学生应对向量问题的转化和化归能力.

1.基底化策略

平面向量基本定理告诉我们：平面上任何一个向量总是可以由两个不共线的向量(基底)线性表出.就该定理本身而言，其内容理解和证明并不难，难就难在对定理的应用上，学生往往对定理的认识不深刻，不清楚有了这个定理能解决什么问题，缺乏通过基底化后解决向量问题的意识.所谓的基底化策略就是选用两个不共线的向量作为基底，将已知和待求的向量用基底表示出来;一般情况下，选作基底的两个向量的模或夹角是已知的，这是可以选择基底化较为明显的信息.

例1如图1，在平行四边形ABCD中，已知AB=8,AD=则的值是____.

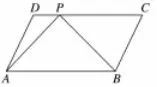
图1

解由得

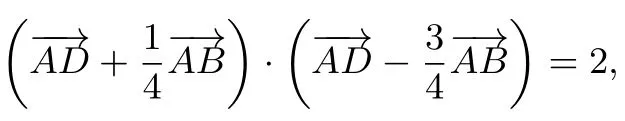
评注本题的解决，充分体现了选择基底化策略的作用，题目中的条件和所求式子，更多的围绕在向量和如果把作为基底，根据平面向量基本定理，将向量和用基底表示出来，然后代入稍作化简，问题就迎刃而解了.

例2如图2，在△ABC中，D是BC的中点，E,F是AD上的两个三等分点，-1，则的值是____.

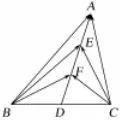
图2

解由

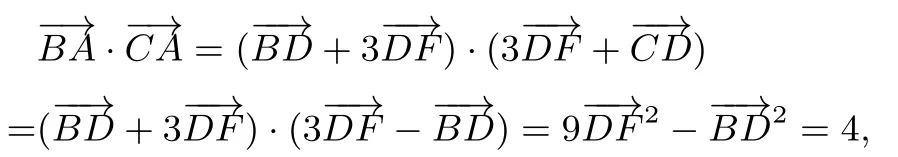
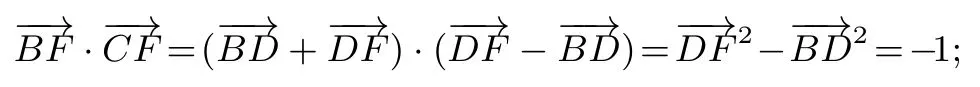
评注由于确定基底的条件不是特别苛刻，两个向量不共线即可，所以基底如何选择很有讲究.本题是2016年江苏高考题，当时得分率较低，题中没有基底化的明显信息，这就需要学生养成选择基底化的意识，题目中的条件和所求式子，更多的围绕在向量(或与的共线向量)，因此，如果选用向量作为基底，根据平面向量基本定理，将已知向量式和要求向量式表示出来，问题也就迎刃而解.

2.坐标化策略

平面向量基本定理在平面向量这一章中起到承上启下的作用，其实质是在对向量进行分解，如果把基底取成互相垂直的单位向量，那么就可在平面直角坐标系中定义平面向量的坐标表示了.所谓的坐标化策略就是把相关已知条件和要求结论中的向量，用坐标表示出来，将向量运算完全代数化;一般情况，涉及正方形、矩形、直角梯形、直角三角形、等边三角形等规则图形，或涉及一些给定一个角度和部分边长等不规则图形为载体的向量问题，均可选择坐标化;向量的坐标化使向量与解析几何建立了联系，使“形”到“数”的转化变为可能，也为很多问题的解决开辟了新的途径，体现了化归与转化、函数与方程等数学思想.

例3如图3，在直角梯形ABCD中，AB//CD，∠ADC=E为BC中点，若则=____.

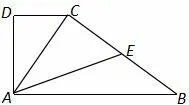
图3

解以A点为坐标原点，AB所在直线为x轴，AD所在直线为y轴，建立平面直角坐标系，设CD=x，则由解得x=1.所以所以

例4已知AD是直角三角形ABC的斜边BC上的高，点P在DA的延长线上，且满足若则的值为____.

解以D点为坐标原点，以BC所在直线为x轴，AD所在直线为y轴，建立平面直角坐标系，设B(b,0)，C(c,0)，P(0,m)，则又所以bc+m2=2.

评注从上述两道例题都有选择坐标化的明显信息，可以看出，坐标化策略对处理一些复杂的向量问题，往往可起到“四两拨千金”的效果;当然，有时坐标轴的选择也很关键，如例2为2019年南京市二模填空题第12题，如果方法选择不恰当，坐标轴选择不合理，处理起来会较为困难;选择坐标化策略，可使题目中各数量关系非常明确，使问题快速解决，让我们深刻体会到了这一点;而且坐标化意识的形成，也为学生后面使用解析法解决问题奠定了基础.

3.数量化策略

向量的数量积对学生来说是一种新的运算，其实该运算是向量与向量相乘和数量与数量相乘相互转化的桥梁，在向量条件的转化中有着重要的应用，一般情况下，数量化的方法就是，对向量等式两边平方或对向量等式两边同时乘以一个向量进行数量积;有时候，学生能否将向量进行数量化，直接影响着问题能否解决;然而，学生大多对数量化的理解不是很到位，因此，培育学生对向量数量化意识，在向量问题的解决中是十分重要的.

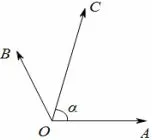
图4

例5如图4，在同一个平面内，向量的模分别为的夹角为α，且tanα=7，与的夹角为45°.若(m,n∈ℝ)，则m+n=____.

解法由题意得

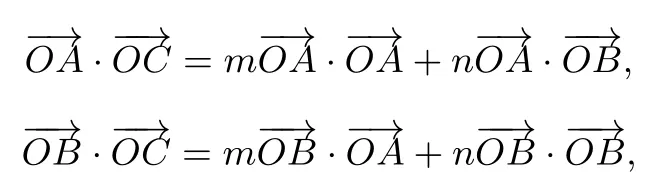
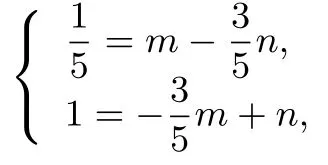
两式相加得m+n=3.

例6在平面直角坐标系xOy中，设直线y=-x+2与圆x2+y2=r2(r＞0)交于A,B两点.若圆上存在一点C，满足则r的值为____.

解由

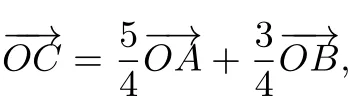
评注上述两道例题中，都是已知一个向量式，然而目标是求实数的值，因此对向量式数量化是解决问题的方向;例5中，是对两边同时分别乘以向量和完成数量化，得到关于m,n两个方程，使问题迎刃而解，例6中，是对两边平方，完成数量化，得到使问题顺利解决.

4.图形化策略

向量与几何有着密切联系，很多向量式子都有着其几何意义，如向量的加减运算对应着平行四边形或三角形，向量的模对应着线段长度，数量积为零的两非零向量对应着互相垂直，向量的数量积被视为一个向量在另一个向量上的投影的乘积等等.所谓的图形化策略，就是把已知条件和所求结论中的向量关系，结合几何意义在图形中表示出来，体现了数形结合的数学思想.但学生在解决问题中往往缺乏选择几何化的意识，不能把数与形有机结合;因此，培育学生的选择几何化应对平面向量问题，显得尤为重要.

例7已知a,b,c是平面向量，若满足且a与b的夹角的正切值为与c的夹角的正切值为则a·c的值是____.

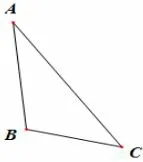
图5

解由向量加法的三角形法则，可构造△ABC(如图5所示)，记所以，由得tanB=-1，得故A,C为锐角，可得由正弦定理所以

例8已知a,b是单位向量，a·b=0，(a-c)·(b-c)=0，则|c|的最大值为____.

图6

解由a,b是单位向量，a·b=0，(a-c)·(b-c)=0，所以可以构造基本图形(如图6所示)，不妨设则b-c，则所以O,A,C,B四点共圆，且该圆是以AB为直径的圆，又是该圆一条弦，故OC的最大值为该圆直径，即

评注上述两道题的解决，需要学生有选择几何化的意识，例7中由加法三角形法则知，可选择构造三角形△ABC，此时向量b的模长与边长AC对应，向量a与b、b与c的夹角分别与∠C、∠A对应，将向量问题置于三角形△ABC中，从而使抽象问题具体化;例8中通过选择构建四点共圆的基本图形，联系圆的相关知识，使问题变得更为简单、直观.

总之，基底化、坐标化、数量化、图形化是应对平面向量问题常见的四种有效的策略，虽然四种策略可各自独立起作用，但实质上，四种策略对应着代数(坐标化、数量化)和几何(基底化和图形化)两个不同视角，若解题时能从多视角思考，一题多解，可使它们互相补充，相得益彰，同时还可以领略不同策略的各自魅力;若解题时面临四种策略的“选择”时，可基于平面向量基本定理，从几何和代数两个不同角度对问题进行全面剖析，看清各种选择之间的联系，把握问题的本质，合理做出选择.