双推进无人艇轨迹跟踪控制系统设计

cd

(武汉理工大学 a.智能交通系统研究中心；b.航运学院；c.国家水运安全工程技术研究中心；d.内河航运技术湖北省重点实验室,武汉 430063)

由于无人艇所处环境的复杂性导致其极易受到外界环境的干扰，以模型为基础的无人艇轨迹跟踪存在着许多不确定因素[1]，因此，实现无人艇对轨迹的精确跟踪需要控制器具有更好的鲁棒性和快速收敛能力。已有的轨迹跟踪控制方法[2-6]都是根据单浆单舵无人艇的横向和纵向位置误差直接计算出无人艇的纵向推力和转船力矩，控制律的设计比较复杂，对无人艇数学模型的精度要求较高，在实用性上稍有不足。与传统的单浆单舵无人艇相比，双推进无人艇可有效降低USV行驶速度对回转控制的影响，减小回转的半径与用时，具有良好的机动性与操纵性，适合在多种特殊的航行环境中使用。本文以“iNav-III”号无人艇为研究对象，尝试采用双闭环轨迹跟踪控制方法实现间接轨迹跟踪控制。

1 控制系统原理

系统原理见图1。

图1 轨迹跟踪控制系统结构

系统采用双闭环控制结构，制导环与控制环分离。基于滑模控制理论设计的双推进无人艇的轨迹跟踪控器属于制导环，基于PID神经网络设计的无人艇航速艏摇角速度协同控制器属于控制环。轨迹跟踪控制器根据参考轨迹的位置坐标和无人艇的实际位置坐标计算出航速艏摇角速度协同控制器所需的期望航速ucmd和期望艏摇角速度ωcmd。航速艏摇角速度控制器将期望航速和艏摇角速度与传感器反馈的实际航速和艏摇角速度进行比较，输出两个推进器的控制信号控制无人艇，从而实现轨迹跟踪。

2 轨迹跟踪控制

2.1 航速艏摇角速度协同控制器

2.1.1 航速艏摇角速度协同控制原理

航速艏摇角速度协同控制器主要由两个单变量PID神经网络(SPIDNN)构成，见图2。

图2 航速艏摇角速度协同控制器

一个SPIDNN的输入分别为期望和实际的纵向速度，其输出代表着双推进无人艇达到该期望纵向速度所需的力的大小。另一个SPIDNN的输入分别为期望的艏摇角速度和船实际的艏摇角速度，其输出代表着双推进无人艇达到期望艏摇角速度所需的力矩大小。将两个SPIDNN的输出进行相加和相减，并分别作为双推进无人艇两个推进器的控制信号控制两个电机的转速，就可以达到双推进无人艇航速艏摇角速度协同控制的效果，并且控制器中的权值可以根据无人艇航速误差和艏摇角速度误差进行学习调整，实现自适应的功能，具有良好的控制效果。

单变量PID神经网络是3层前向神经网络，具有动态非线性的特点[8]，结构见图3。具有输入层、隐含层、输出层，各层神经元的数目分别是2、3、1。输入层两个输入信号分别是指令信号和被控对象的输出信号，隐含层为比例、积分、微分神经元，分别对应于PID控制的3个环节，其传递函数分别为比例、积分、微分函数。输入信息先通过隐含层的3个动态神经元处理，按照神经元权值进行加权组合得到结果，最后结果在输出层输出。SPIDNN先将输入信息向前传播得到输出，然后将得到的误差信息反向传播，对网络的权值进行修正，达到自适应调节控制器参数的效果。

图3 PID神经网络控制结构

2.1.2 SPIDNN前向算法

SPIDNN输入层的输入与输出相等，隐层第i个神经元的输入为

(1)

式中：1wij为输入层第j个节点至隐层第i个节点的权值。

隐含层比例、积分、微分神经元的输出qi(k),i=1、2、3的计算如下。

1)比例环节。

(2)

2)积分环节。

3)微分环节。

输出层神经元的输入是隐层各节点输出的加权和。

(5)

式中：2wI为隐含层节点i至输出层节点的权值。

输出层神经元的输出，即网络的输出为

(6)

2.1.3 SPIDNN反向学习算法

PID与BP神经网络的反向学习算法相同，都采用梯度下降法。反向学习的目的都是将误差控制在较小的范围内，故将目标函数定义为

(7)

经k步训练，调整隐含层至输出层权值算法。

(8)

式中：η2为2w的学习步长。

(9)

经k步训练，调整输入层至隐含层权值算法。

(10)

式中：η1为1w的学习步长。

(11)

2.2 基于全局稳定的滑模轨迹跟踪控制器

2.2.1 轨迹跟踪控制原理

滑模轨迹跟踪控制器是由内外环构成的控制系统，位置子系统为外环，姿态子系统为内环。外环的位置控制系统根据位置误差产生速度控制指令vr和期望航向角θd，期望航向角θd再被传递给内环的姿态控制系统，姿态控制系统通过滑模控制算法实现对中间指令信号的跟踪，并产生艏摇角速度控制指令ωr。滑模轨迹控制器将产生的航速控制指令和艏摇角速度控制指令传递给航速艏摇角速度协同控制器，实现对参考轨迹的跟踪。原理见图4。

图4 轨迹跟踪控制器原理示意

2.2.2 位置控制律设计

通过设计位置控制律，实现x跟踪xd，y跟踪yd。取理想轨迹[xdyd]，则误差跟踪方程为

(12)

式中：xe=x-xd；ye=y-yd。

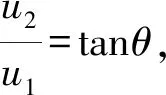
(13)

设计理想的位姿指令[xdyd]时，需要使θd的值域满足(-π/2,π/2)。

设计控制律为

(14)

式中：a、p1>0;b、p2>0。

则模型变为

(15)

根据文献[9]提出的动态系统全局渐进稳定定理可实现xe→0，ye→0。

动态系统全局渐进稳定定理可表述为

(16)

式中：α、k>0。则当t→∞时，η→0。

至此，可得实际的位置控制律为

(17)

2.2.3 姿态控制律设计

通过设计姿态控制律ω，实现无人艇航向角θ跟踪θd。取θe=θ-θd，取滑模函数为s=θe，则

设计姿态控制律为

(18)

式中：k>0；η>0。

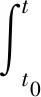
(19)

式中：α为任意常数。

Vθ(t)≤e-2k(t-t0)Vθ(t0)

(20)

可见Vθ(t)为指数收敛，即s为指数收敛，从而θe指数收敛，艏向角θ指数收敛于θd，收敛速度取决于控制律中k的值。

3 实船实验

“iNav-III”号双推进无人艇是无舵双桨的形式，该双推进无人艇长1.75 m、宽0.75 m、吃水0.12～0.13 m。艇尾装有两个推进器，最大航速可达2 m/s，最大艏摇角速度可达40 (°)/s。艇内装有电子罗经、惯性测量与导航系统、差分GPS以及数传电台。

实船实验在武汉理工大学露天操纵船池进行，实验场景见图5。实船实验中，将SPIDNN参考指令信号的输入神经元与隐含层间的初始权重置为1，将反馈信号与隐含层间的初始权重置为-1，将传统PID控制器的经验参数用于SPIDNN隐含层至输出层的初始权重，两个单变量PID神经网络隐含层至输出层的初始权值2w1=0.7，2w2=0.2，2w3=0.1。学习速率η1和η2皆置为0.05。滑模轨迹跟踪控制器中a=0.5，b=0.5，p1=0.4，p2=0.4，k=0.2，η=0.1。

图5 双推进无人艇及其试验场景

为验证所设计的基于PID神经网络的航速艏摇角速度协同控制器的实际控制效果，进行航速为1.0 m/s，艏摇角速度为0.2 rad/s的双推进无人艇航速艏摇角速度协同控制实验。将其与普通的PID控制器进行对比，普通PID控制器的控制参数与PID神经网络隐含层至输出层的初始权重相同，航速和艏摇角速度控制结果分别见图6、7。

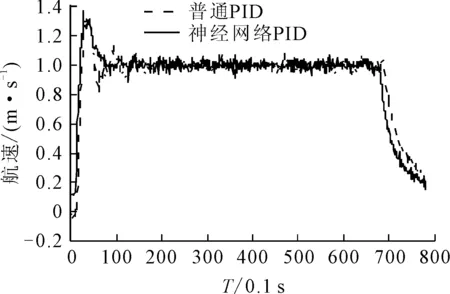
图6 航速控制

图7 艏摇角速度控制

实验结果表明，基于PID神经网络的航速艏摇角速度协同控制器能够快速而有效地控制无人艇的艏向速度和艏摇角速度收敛到较小的误差范围内，并且由于神经网络自学习的能力使其能够得到比普通PID更好的控制效果。

进行直线轨迹跟踪实验，无人艇所跟踪的直线轨迹用函数表达如下。

(22)

直线轨迹跟踪试验效果见图8，无人艇的初始速度为0 m/s，航向角为100°。轨迹跟踪过程中的位置误差见图9，稳定后最大位置误差为1.232 m，实验结果表明，所设计的轨迹跟踪控制器能够较好地实现对直线轨迹的跟踪。

图8 直线轨迹跟踪的路径

图9 直线轨迹跟踪的位置误差

无人艇在跟踪过程中不可能一直走直线，当遇到障碍物或有任务要求时需要具有对曲线轨迹进行跟踪的能力，因此，设计如式(23)所示的圆形跟踪轨迹进行轨迹跟踪试验。

(23)

实验结果见图10，无人艇的初始速度为0，初始航向角为94°，轨迹跟踪位置误差见图11，最大位置误差为1.205 m。

图10 圆形轨迹跟踪路径

图11 圆形轨迹跟踪位置误差

试验结果表明，所设计的轨迹跟踪控制器能够较好的实现对曲线轨迹的跟踪。

为了验证轨迹跟踪控制器对非圆曲线的跟踪能力，设计一组参考轨迹为正弦曲线的轨迹跟踪试验，参考轨迹的函数表达式如下。

(24)

双推进无人艇对正弦曲线进行轨迹跟踪的轨迹见图12，无人艇的初始速度为0，初始航向角为24°，轨迹跟踪位置误差见图13，跟踪稳定后的最大误差为0.907 m。圆形曲线和正弦曲线轨迹跟踪结果表明，轨迹跟踪控制器能够实现对复杂曲线的轨迹跟踪。

图12 正弦曲线轨迹跟踪的轨迹

图13 正弦曲线轨迹跟踪的位置误差

对以上3组轨迹跟踪实验稳定后的轨迹跟踪误差数据进行统计，所有轨迹的轨迹跟踪平均误差均小于0.661 m，证明所设计的轨迹跟踪控制器具有良好的控制效果。进一步对轨迹跟踪位置误差图进行观察后可以发现，虽然设计的轨迹跟踪控制系统能够让无人艇实现对曲线和直线轨迹较为精确地跟踪，但是轨迹跟踪的误差在进入稳定状态后，会在零到最大跟踪误差值之间进行波动。分析其原因，一方面是使用滑模控制算法设计控制律时，由于开关函数的存在，会产生滑模控制结构本质上的抖振现象；另一方面是由于从控制信号发送到执行机构执行需要一段响应时间以及受到无人艇自身惯性的影响，无人艇不可能立即达到期望的运动状态。

4 结论

1)以双推进无人艇为研究对象，采用PID神经网络和滑模变结构控制算法对无人艇的轨迹跟踪控制系统进行研究，提出的双闭环轨迹跟踪控制方法运用到实船实验中，实现了对各种直线和曲线轨迹的跟踪控制。

2)在实船实验中，无人艇的轨迹跟踪误差会在一小段范围内抖动。这是由于滑模变结构控制在本质上的不连续开关特性导致的抖振现象，抖振不可以完全消除，但可以通过调整滑模控制律的参数减少抖振的影响。

3)针对实船实验中轨迹跟踪存在着的抖振问题，下一步的研究可以考虑根据位置误差自适应调整控制律的参数得到最优的控制效果，实现更加精确的轨迹跟踪。