中小邮轮滑道拉移上驳船底结构强度计算方法

张卫1,，葛珅玮，朱红娟

(1.上海交通大学 船舶与海洋建筑工程学院，上海 200240；2.招商局邮轮制造有限公司，江苏 南通 226005)

受到成本等因素的制约，中小邮轮通常平地建造[1]，下水时，在邮轮底部铺设滑道，通过拉移滑道将邮轮船体拉移至半潜驳上之后下水[2]。受到潮汐、驳船压载精度，以及压载滞后等问题的制约，驳船的甲板面与船台水平面常存在一定的高度差，导致船底结构在通过驳船与船台交界处时由于自身重力产生严重的应力集中。由于接触不均匀，使得船底艏艉支撑处的局部结构应力、变形都很大。邮轮结构所采用的钢板都很薄，极易发生局部损伤破坏，造成舱室破坏、设备受损。现有的技术针对中小邮轮滑道拉移上驳时船底结构强度的分析研究较少，未见完整、精确的计算方法。针对这一问题，基于有限元理论，提出一种拉移上驳过程中船底结构强度的计算方法，以期精确、快速计算中小邮轮在滑道拉移上驳过程中的应力分布。

1 简化有限元模型

全船有限元分析能够全面地评估全船结构在各种载荷工况下的应力分布与变形，在整船强度分析中被广泛使用[3-4]。但该方法需要建立完整的全船模型，工作量巨大，在时间非常紧迫的情况下，不是特别适用。

邮轮结构静止于滑道上或是在拉移过程中，主要由船底结构承受重力及由重力产生的弯矩。在弯矩作用下，结构产生的应力如下。

σ(x)=M(x)/Z(x)

(1)

式中：Z(x)为完整截面的剖面模数。

相对于主船体结构，上层建筑结构较弱，参与弯曲强度较少。假设上层建筑不参与船体刚度，此时船体截面的剖面模数记为Z1(x)。

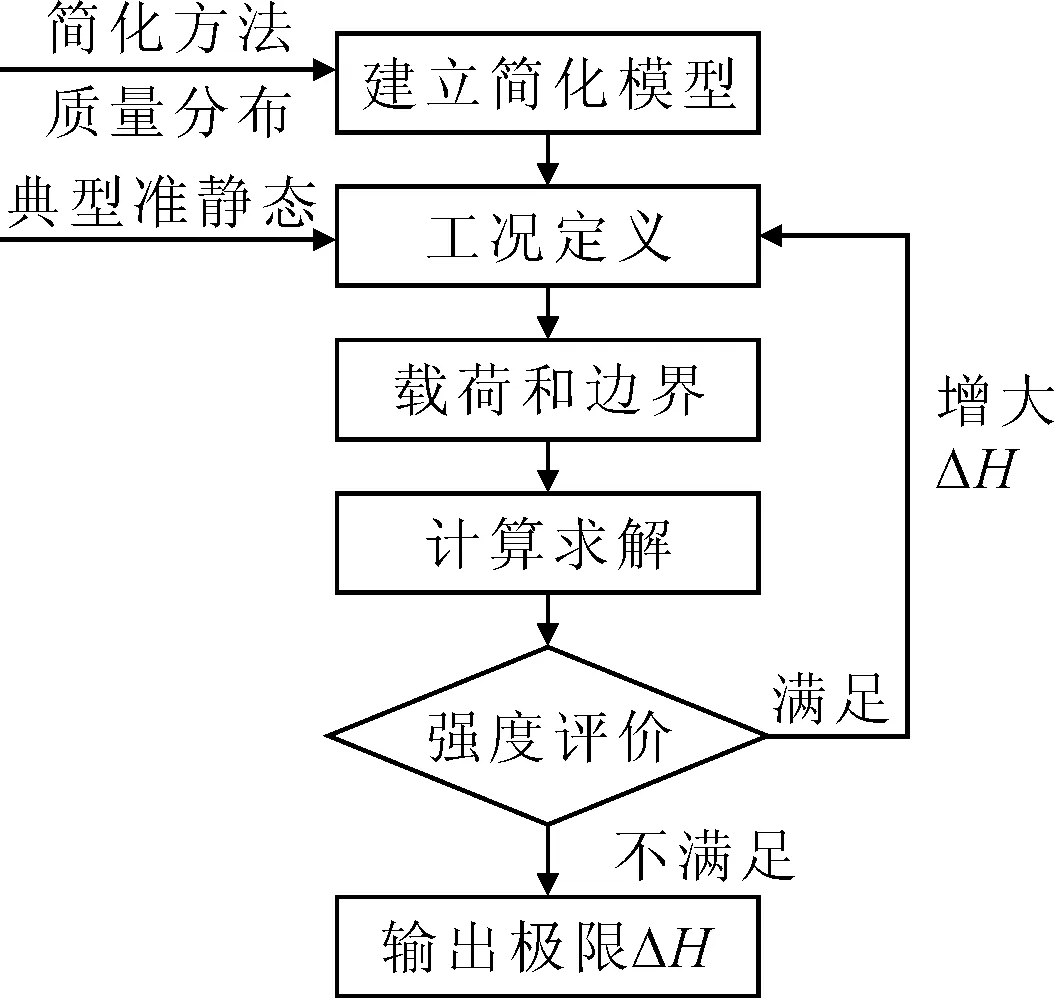
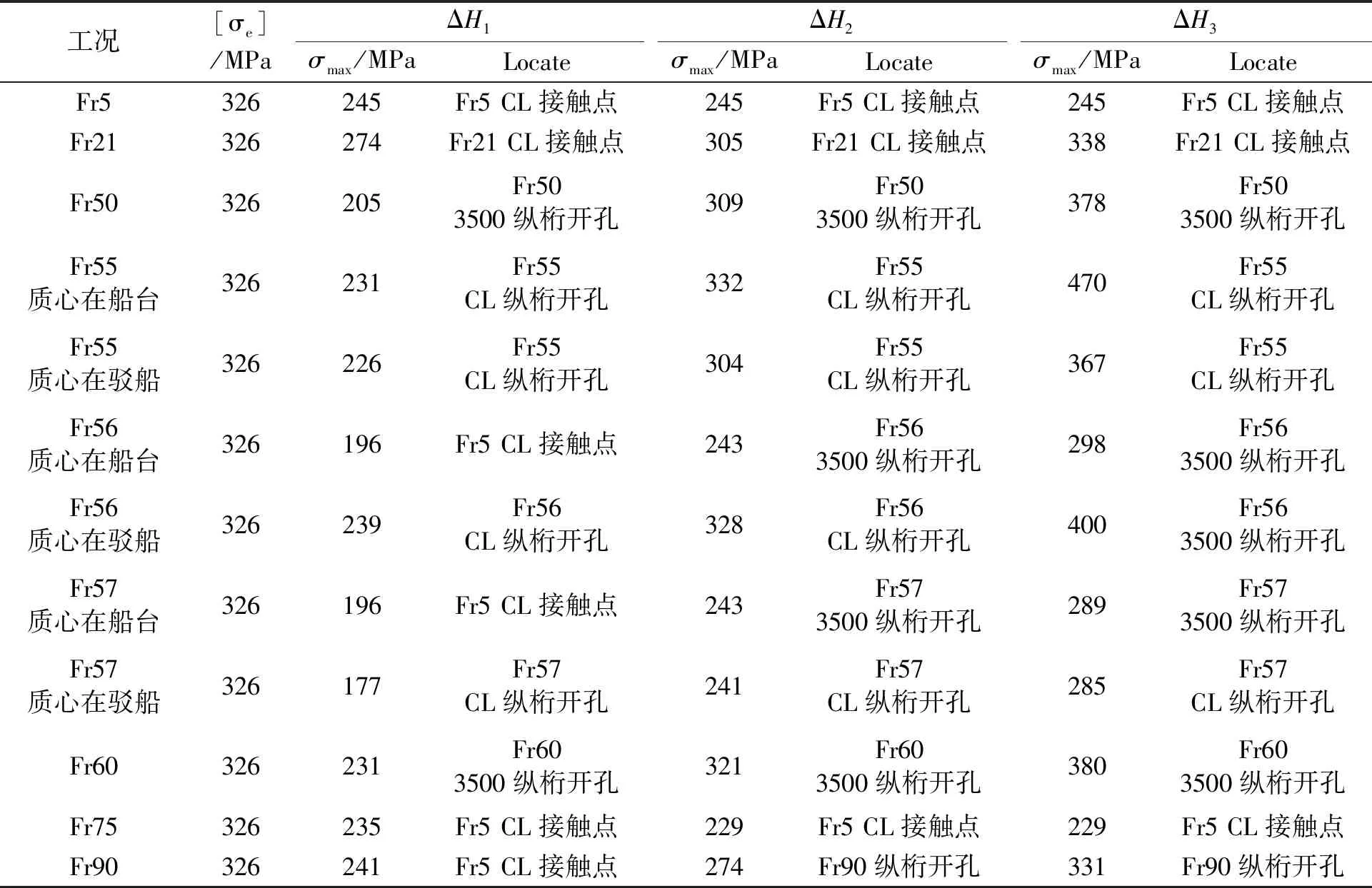
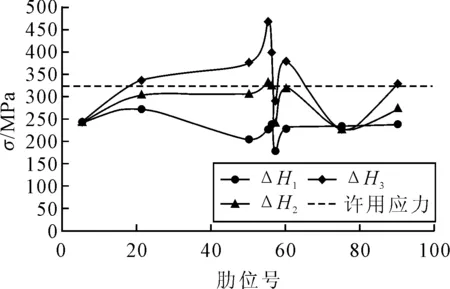
Z1(x)

(2)

由式(1)可知，由于少了上层建筑所贡献的刚度，船体梁的应力一定会增加，造成计算所得应力偏危险。考虑施工现场的一些不确定因素，按此应力进行强度评估，留有一定余量，对于实船作业有利。

在保证船体结构一定刚度与强度的情况下，简化全船有限元模型：建立主船体结构有限元模型；上层建筑采用等效质量点的形式，沿着船长方向，将结构划分为几个段，每段的质量按照质心坐标位置增加到结构上，保证结构质量与实际质量一致；为了得到船底结构较为准确的应力分布，船底结构需要精确模拟。

2 计算方法

2.1 准静态方法

船体结构拉移上驳的过程是一个动态的过程，由于拉移速度很低，整体结构是一个力学平衡的系统。对于某一时刻，认为结构是静止的状态，对该过程进行静态计算求解。

2.2 计算工况

基于2.1的假设，若对滑道拉移上驳过程中的每一个时刻都进行分析，则计算工况非常多。考虑到船体结构的强弱及型线的变化，选择结构相对较弱及外板型线突变的位置，将这些位置在经过驳船与船台交界处(以下称交界处)时的准静态体系作为典型分析工况。

2.3 高度误差模拟

2.3.1 极限高度差

驳船静止于水面上，由于潮汐及驳船压载精度的原因，驳船的甲板面与船台水平面常存在一定的高度差。在拉移过程中，由于驳船载质量比邮轮质量大，且上驳速度非常慢，因此，驳船基本一直保持在水平状态。实际操作中，驳船的甲板面通常会低于船台平面。基于准静态的考虑，假设驳船与船台平面的高度差为ΔH，则在不同的ΔH下，船底的应力分布会也不同。若在某一ΔHi下，船底结构的最大应力达到强度极限，则该高度差即为驳船甲板面与船台高度差允许的极限值。见图1。

图1 邮轮拉移过程

2.3.2 有限元模拟

当船体局部结构通过交界处时，局部结构会由于重力的作用发生垂向变形Δh。

当Δh>ΔH时，邮轮结构与驳船甲板面相接触，驳船吃水增大，驳船所受到的浮力将会变大，增大的浮力如下。

ΔF=ρgΔV

(3)

驳船所受到的浮力，将成为邮轮结构的一部分支撑力。

当Δh≤ΔH时，则船底结构不会与驳船甲板面接触，邮轮局部结构的质量将由其自身结构承受。

基于上述考虑，将驳船结构视为一个只能承受压力而不能提供拉力的非连接支撑结构，该结构的刚度为

(4)

NX Nastran的单元库中，提供了一种非线性接触单元(Gap单元)，不仅可以提供压缩刚度，还能提供拉伸刚度。借助于这种单元，将拉伸刚度定义为0，初始间隙定义为ΔHi，能很好地模拟上述计算。

2.4 评估标准

各大船级社对结构强度的评估一般采用许用应力的方法。IACS评估公式如下[5]。

(5)

式中：σe为板单元中心等效应力；K为材料系数，HT36钢，K=0.72。

式(5)的本质是利用材料的屈服极限与材料的种类、特性有关，而与具体的船型并无直接关系，因此，采用该式进行强度评估。

2.5 计算流程

在简化全船有限元模型的基础上，确定邮轮滑道拉移上驳船底强度计算方法流程，见图2。

图2 滑道拉移上驳极限ΔH计算流程

3 邮轮拉移上驳计算

3.1 邮轮主尺信息

表1 某邮轮主尺度

该邮轮拥有多层甲板，其中四层甲板以上是上层建筑，部分参与全船总纵强度；四甲板以下为主船体结构，直接参与总纵强度。船底采用双层结构，艏艉部分外板采用横骨架式进行冰区加强。

3.2 简化有限元模型

利用Femap软件建立简化全船有限元模型，见图3。有限元网格大小约为肋骨间距×纵骨间距。

图3 简化全船有限元模型

甲板、外板、舱壁、横梁腹板、纵桁腹板等主要结构采用板单元建模；纵骨、肋骨、横梁面板、纵桁面板、支柱等采用梁单元建模；主机、发电机、螺旋桨等设备采用质量单元建模；上层建筑及其部分主船体结构仅考虑重量，采用质量单元建模。这些质量单元通过MPC与结构相连，关联Tx、Ty、Tz3个自由度。

由于模型简化，很多舾装件、电装支架、小型设备等质量并未包含在该模型中，故采用放大重力加速度的方法，保证模型的重力与实船完全一致。此外，通过结构密度的调整，使得结构质心与实船吻合。

3.3 静止于滑道

邮轮结构在搭载时，船底沿船台方向共铺设5排墩木。受到设备的制约，铺设滑道时，船底共铺设3条滑道，分别位于CL纵桁、左右舷各距CL距离3 500的纵桁(以下称3 500纵桁)。由于艏艉线型收缩，艏艉较长范围内仅1条滑道支持，故需要评估船体结构仅静止于滑道上时的结构强度。载荷为船体重力，边界条件取底部与滑道相连处简支约束(Tx=Ty=Tz=0)。通过计算，得到结构应力分布见图4。

图4 自重下船底结构的应力分布

由图4可见，在自重作用下，整个船体结构强度满足许用应力的要求。但艉柱附近外板处的应力相对较高，这是由于除了艉柱正上方的质量，艉柱至艉封板之间的质量也作用在艉柱附近支持点上，造成了该处应力较大。这将是后续拉移过程中的重点观测位置。

3.4 结构变形极限分析

假设驳船与船台的高度差非常大，邮轮在拉移过程中不会与驳船甲板面接触。当船体质心接近交界处、结构尚处于平衡状态时，船体结构将出现垂向变形最大的极限状态。

基于简化模型，对船体结构与船台滑道连接处做简支约束(Tx=Ty=Tz=0)，求解之后，得到变形云图见图5。

图5 极限变形云图

由图5可见，在极限状态下，结构的最大垂向变形是444 mm，艉柱最底部的最大垂向变形为354 mm。此时，结构最大应力高达1 000 MPa，结构发生破坏。因此，这种情况不允许出现。

由于驳船的压载控制精度一般在10 mm左右，因此，计算中，以10 mm为一档，对ΔH取3个值，ΔH1=10 mm，ΔH2=20 mm，ΔH3=30 mm。

3.5 不同工况下的计算

考虑到船体结构剖面的强弱及其型线的变化，选取Fr5、Fr21、Fr50、Fr55、Fr56、Fr57、Fr60、Fr75、Fr90这些剖面通过交界处的准静态作为分析对象。在计算中，质心数据来自于物料统计，在当时阶段无法通过实验获取，因此，该数据与实船质心位置可能存在一定偏差。出于安全考虑，对质心附近Fr55、Fr56、Fr57这三个剖面分别计算两种准静态，即分别假设船体质心在驳船位置与质心在船台位置两种状态。当质心在船台上，船艉至船舯将会发生垂向变形，艉部滑道用Gap单元模拟；当质心在驳船上面，则船艏至船舯将会发生垂向变形，艏部滑道处用Gap单元模拟。

在分析时，准静态过程从ΔH1开始计算，若ΔH1满足强度要求，则继续计算ΔH2；若ΔH2满足强度要求，则继续计算ΔH3。根据3.4中ΔH的取值，计算36个准静态工况。见表2。

3.6 结果分析

由表2可见，当船台与驳船甲板面的高度差ΔH在10 mm以内时，船底结构满足强度要求；当ΔH在20 mm以内时，除船舯Fr55/Fr56处通过交界处时(质心在船台上)底部开孔不满足要求，其他主要船底结构均满足需用应力要求；当ΔH在30 mm及以上时，船底结构基本都不满足许用应力要求，超出应力指标很多，因此，当船台与驳船甲板面的高度差控制在10 mm以内时，无需补强就能满足强度要求。

表2 计算结果汇总

从最大应力所在位置可以看出，ΔH1、ΔH2下各工况的最大应力位置均发生在船台与驳船甲板面的交界处。这是由于船体结构在船台边缘位置发生垂向变形，除艏艉部最低点与驳船或船台接触时提供一定支撑力，悬空部分结构产生的弯矩均由交界处的截面承受，因此在该处产生最大的应力。而ΔH1下“Fr56/Fr57质心在船台上”时，结构最大应力出现在艉部最低点与驳船甲板面接触位置，这是由于船体悬空结构的垂向重力主要由该点提供，在该处产生了较大的应力集中；但是又由于ΔH1值较小，悬空结构自重在交界处断面产生的弯矩较小，因此导致应力较小。

基于表2的计算结果，沿着船长方向绘制船底结构在滑道拉移过程中的应力变化曲线(Fr55～Fr57考虑最危险的状态)，见图6。

图6 船底结构滑道拉移过程最大应力变化

由图6可见，在拉移过程中，随着船体结构在驳船上的质量越来越多，船底在交界处产生的应力也越来越大，当船体质心完全移至驳船上后，继续拉移，船底的最大应力呈现出先降低后增加的变化趋势。船舯位置附近应力突变，是因为该处船底设有电梯，底部纵桁上有开孔，产生受力不均、应力集中的现象。

在驳船操作时，应严格控制压载水，使得船台与驳船甲板面的高度差在10 mm以内；若对船舯纵桁开孔适当补强，则ΔH可提高至20 mm，但不建议超过20 mm；从应力上看，ΔH=30 mm时，结构应超标很多，极有可能发生损伤。

4 结论

1)该方法可用于计算邮轮结构在拉移过程中船底的应力分布，计算方法高效、结果偏安全。

2)预报邮轮结构在拉移过程中船台与驳船甲板面高度差ΔH的极限值，可为驳船的压载操作提供参考，也可为其他中小邮轮的拉移上驳作业提供参考。

3)给出了邮轮船底结构的应力分布规律，可为邮轮船底结构的预先补强提供依据。