脱粘损伤对压缩载荷下夹芯复合材料L形节点承载能力的影响

(武汉理工大学 交通学院，武汉 430063)

复合材料因为具有很高的比强度、比刚度和较强的耐腐蚀性而被广泛应用于船舶与海洋工程结构物中[1-2]。夹芯复合材料L形节点是复合材料船体中典型的局部结构，可用以连接甲板和舷侧[3]。夹芯复合材料L形节点的主要破坏位置在圆弧肘板上[4-5]，并且圆弧肘板处的脱粘损伤是其主要的损伤模式[6-7]。夹芯结构在制造和使用过程中形成的脱粘损伤[8-9]对L形节点甚至主船体都将造成安全隐患。目前，关于夹芯复合材料L形节点的研究主要集中在完整结构上，未见对含有脱粘损伤的L形节点的研究报道。

考虑到工程实际中需要对L形节点进行损伤检测，根据损伤情况评估L形节点的使用性能。因此，考虑采用渐进失效分析方法和内聚力模形对夹芯复合材料L形节点进行模拟分析，在节点的圆弧肘板引入面芯脱粘损伤，探讨脱粘损伤的位置及几何尺寸对压缩载荷下的L形节点极限承载力的影响，为L形节点损伤评估提供依据。

1 有限元模型

以文献[7]中的L形节点为研究对象，节点由成105°夹角的两块复合材料夹芯板和加强筋组成，包括一道纵向和两道横向加强筋，见图1。

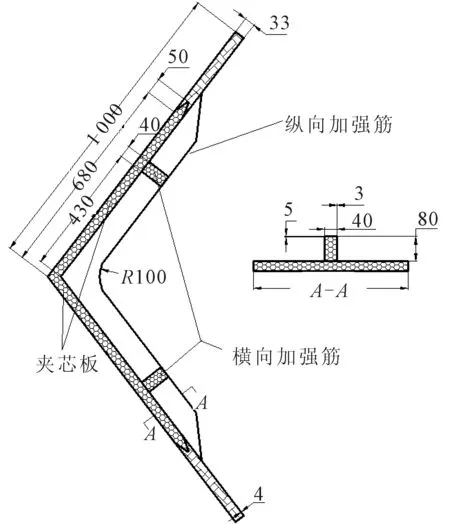
图1 试件尺寸

将L形加强筋的PVC固定在夹芯板的相应位置，然后在其表面糊制复合材料，复合材料和PVC之间通过胶层粘接。复合材料面板为正交编织的玻璃纤维增强塑料(glass-fiber reinforced plastic，GFRP)，夹芯的材料为聚氯乙烯(Polyvinyl Chloride，PVC)，胶层材料是环氧树脂，材料参数见表1～3。

表1 GFRP材料参数

表2 PVC材料参数

表3 GFRP材料强度 MPa

采用Abaqus建立节点的有限元模型，采用实体单元C3D8R模拟复合材料面板和夹芯，采用内聚力单元COH3D8模拟复合材料和夹芯之间的胶层。试件两端通过工装固定，在上端施加向下的压缩载荷，见图2。

图2 试验加载

为了与试验的边界条件保持一致，数值模拟中将试件底端刚性固定，在试件上端截面的几何中心处建立参考点，并将试件上端节点与参考点耦合，保证上端节点和参考点的位移一致，上端节点的转角保持自由。在参考点上施加向下的载荷，参考点的位置以及载荷条件见图3。

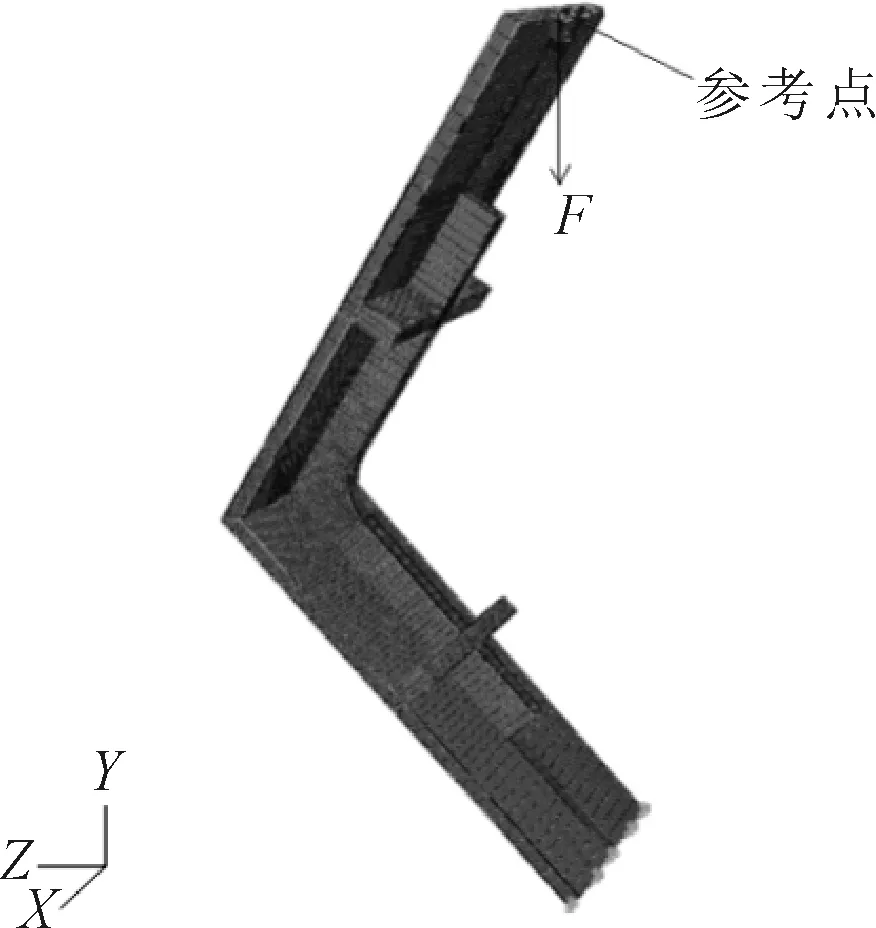
图3 有限元模型

2 材料失效模拟

采用渐进失效分析模拟夹芯复合材料L形节点的复合材料面板失效。渐进失效分析的一般流程是进行有限元计算，提取单元应力，依据失效准则判断单元是否发生失效，然后根据不同的失效类形对刚度矩阵进行折减退化，重复计算直至结构最终破坏。根据正交编织纤维的特点，定义4种失效模式：①方向纤维失效(FV1)；②方向纤维失效(FV2)；③纤维基体剪切失效(FV3)；④分层失效(FV4)。将Shokrieh-Hashin[10]准则进行改进作为GFRP正交向编织纤维复合材料的失效准则，其表达形式如下。

1)1方向纤维失效。

(1)

2)2方向纤维失效。

(2)

3)纤维基体剪切失效。

(3)

4)分层失效。

(4)

PVC夹芯材料的本构关系采用理想弹塑性模型，PVC泡沫的屈服应力为σ=3 MPa，当夹芯的von Mises应力达到屈服应力时，夹芯材料发生破坏。L形节点的夹芯和复合材料板之间采用环氧树脂粘接，在数值模拟中采用内聚力模型来模拟这些粘接的胶层界面。采用二次名义应力准则(见式(5))判断内聚力单元损伤的发生，采用基于能量释放率的B-K准则[11](见式(6))判断单元最终失效。通过Abaqus软件输出刚度退化参数(scalar stiffness degradation，SDEG)判断面芯脱粘失效，SDEG>0，则单元开始失效；SDEG=1，表明单元完全失效。

(5)

式中：Tn、Ts和Tt是3个方向的界面强度。

(6)

式中：GⅠC、GⅡC为临界应变能释放率，对于环氧树脂材料，η为材料常数，一般取η=1.45。

3 模拟结果

3.1 载荷位移曲线

提取数值模拟的载荷-位移曲线与文献[7]中的试验数据进行比较。在初始阶段，载荷与位移呈线性关系，试验中L形节点的刚度与计算的刚度基本一致,见图4。

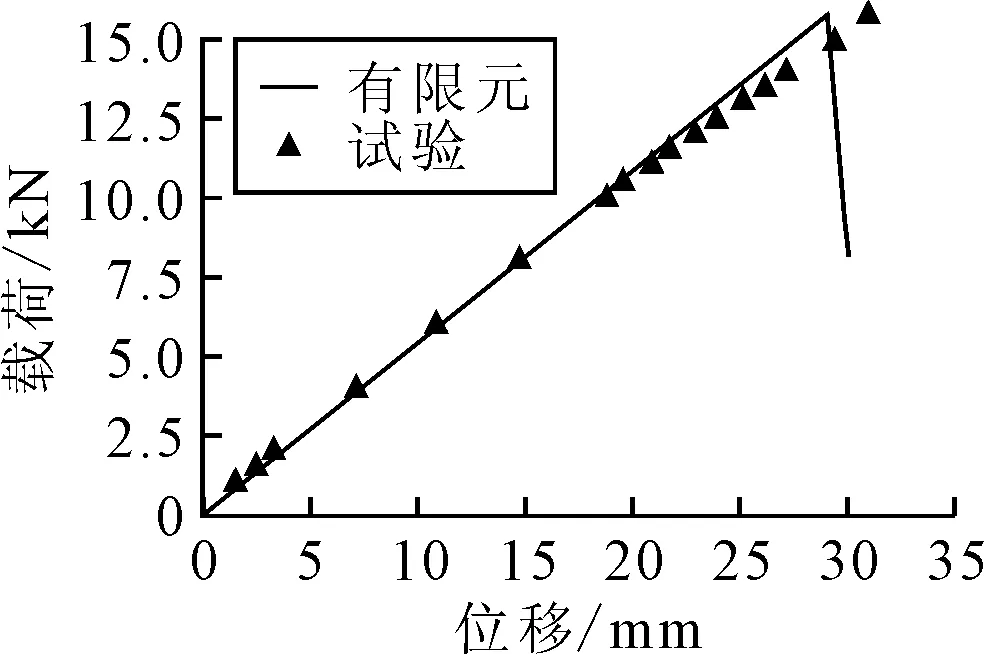
图4 试验与有限元模拟的载荷位移对比

由于复合材料是脆性材料，所以在试验中，到达极限载荷以后，节点发生脆性断裂，无法继续承受载荷，采集的数据也随即停止，采集到的最后的载荷值即为极限载荷；在有限元计算中，当载荷到达临界值，有限元软件基于失效准则判定复合材料发生失效。由于复合材料失效进程很快，结构在一瞬间就失去了承载能力，所以随着位移继续增加，载荷发生陡降。试验中L形节点在压缩载荷下的极限承载力为15.809 kN，平均刚度为517.580 N/mm，数值模拟得出压缩载荷下的极限承载力为15.798 kN，平均刚度546.223 N/mm，极限承载力误差为0.07%，平均刚度相对误差为-5.5%。

3.2 失效模式

试验与数值模拟中L形节点的失效模式对比见图5。

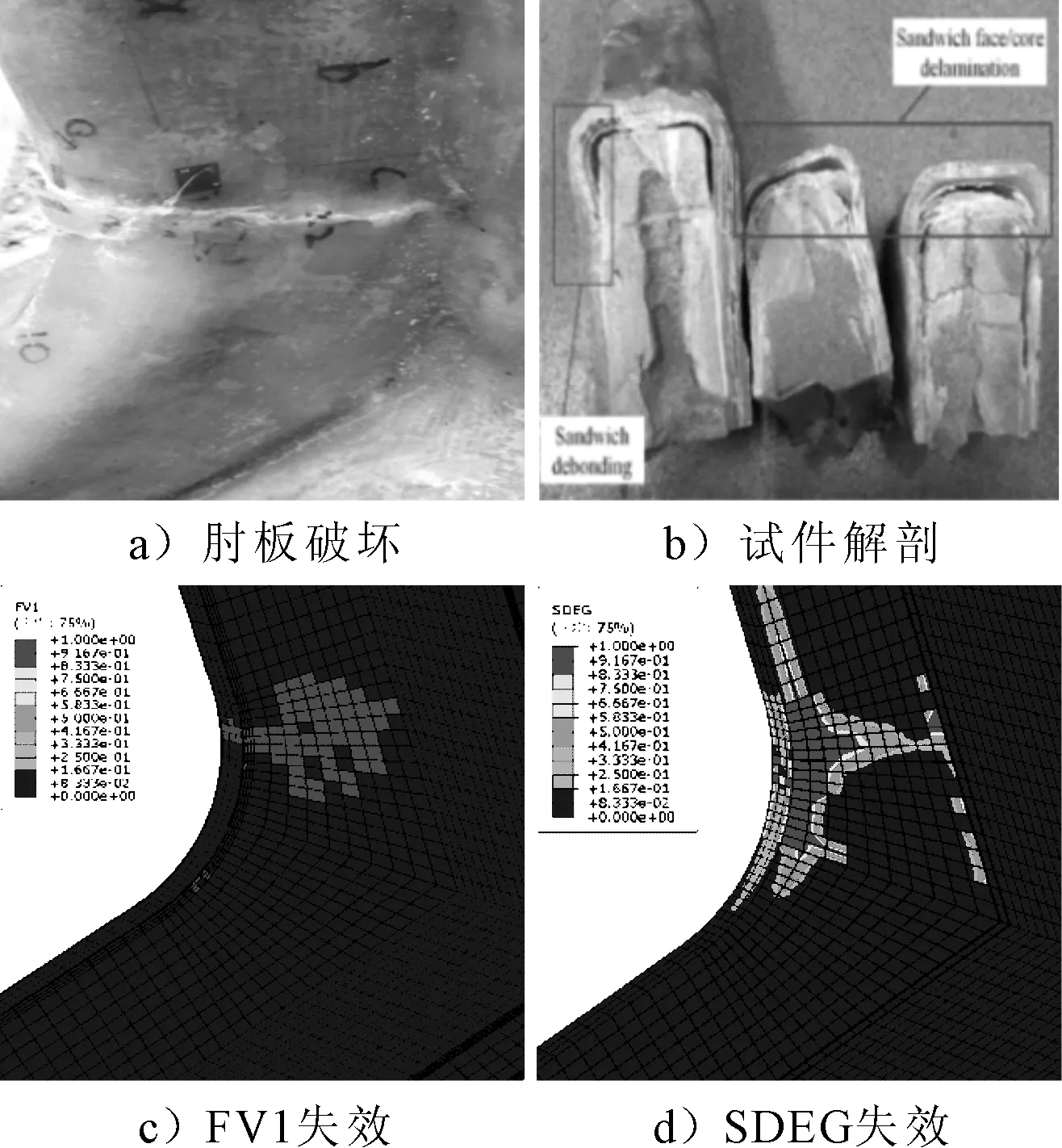
图5 失效模式对比

试验中L形节点的主要破坏形式是圆弧肘板处的裂纹，裂纹处纤维发生断裂，部分纤维脱落，见图5a)。试件在裂纹处的解剖图见图5b)，解剖图显示破坏位置发生面芯脱粘。有限元计算结果显示，L形节点的主要失效模式为纤维失效和脱粘失效。图5c)显示的是1方向纤维失效(FV1)情况，根据材料方向的定义，该失效模式与图5a)中的裂纹相对应，并且大致位置也相同。圆弧肘板的脱黏失效(SDEG)见图5d)，内聚力单元失效表征了图5b)中面板芯材之间的脱粘情况。从图5的对比可以看出，数值模拟得出的失效模式与试验中L形节点实际发生的失效情况一致性较高。

上述研究表明，数值模拟方法能够对夹芯复合材料L形节点在压缩载荷下的极限承载力作出较为合理地预测，并且能够对节点的复合材料面板失效和面芯脱粘失效进行有效地模拟。由于在实际应用中，夹芯结构容易产生脱粘损伤，对L形节点的安全性带来影响。对含有脱粘损伤的L形节点进行模拟，相当于在节点的内聚力单元发生失效之后对其进行模拟。因此，可以继续采用该数值模拟方法探究脱粘损伤对复合材料L形节点在压缩载荷下的极限承载力的影响。

4 脱粘损伤的影响

4.1 脱粘损伤位置对极限承载力的影响

考虑到圆弧肘板本身应力水平较高，外部载荷作用下易于发生损伤问题，因此，分别在圆弧肘板中心和上端引入两处圆形脱粘损伤，损伤半径为20 mm，位置见图6。

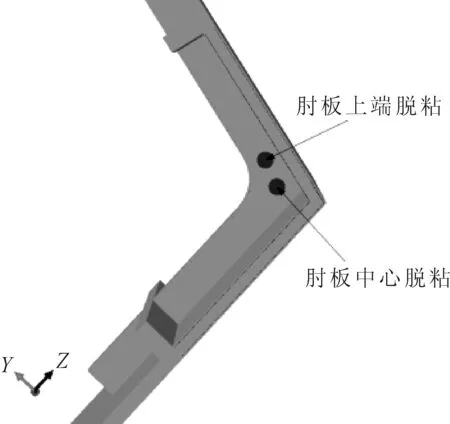
图6 脱粘损伤位置

删除损伤部分的内聚力单元[12-13]，细化这部分网格，在损伤位置的面板向外侧施加0.1 mm的初始位移使夹芯和面板分离来模拟初始损伤。计算得出压缩载荷下含有面芯脱粘损伤的L形节点的载荷位移，见图7。

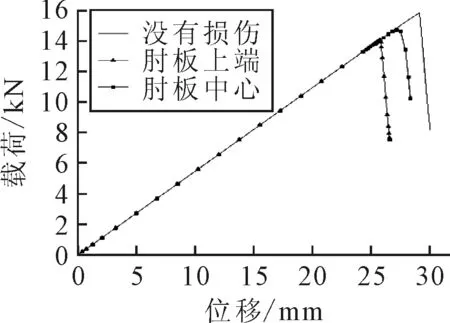
图7 含损伤和不含损伤节点的载荷-位移变化

数值模拟结果显示，脱粘损伤对节点的刚度基本没有影响，对节点在压缩载荷下的极限承载力有一定影响。在肘板中心含有脱粘损伤的节点极限承载力为14.690 kN，相对不含损伤的节点下降7.0%，在圆弧肘板上端含有脱粘损伤的节点极限承载力为14.023 kN，相对不含损伤的节点降低11.2%。

由于最终失效都发生在L形节点的圆弧肘板处，所以主要以该区域为研究对象。不同位置含有初始脱粘损伤的L形节点发生最终失效时单元的FV1失效情况见图8，圆弧肘板处不同失效模式开始发生时的载荷见表4。

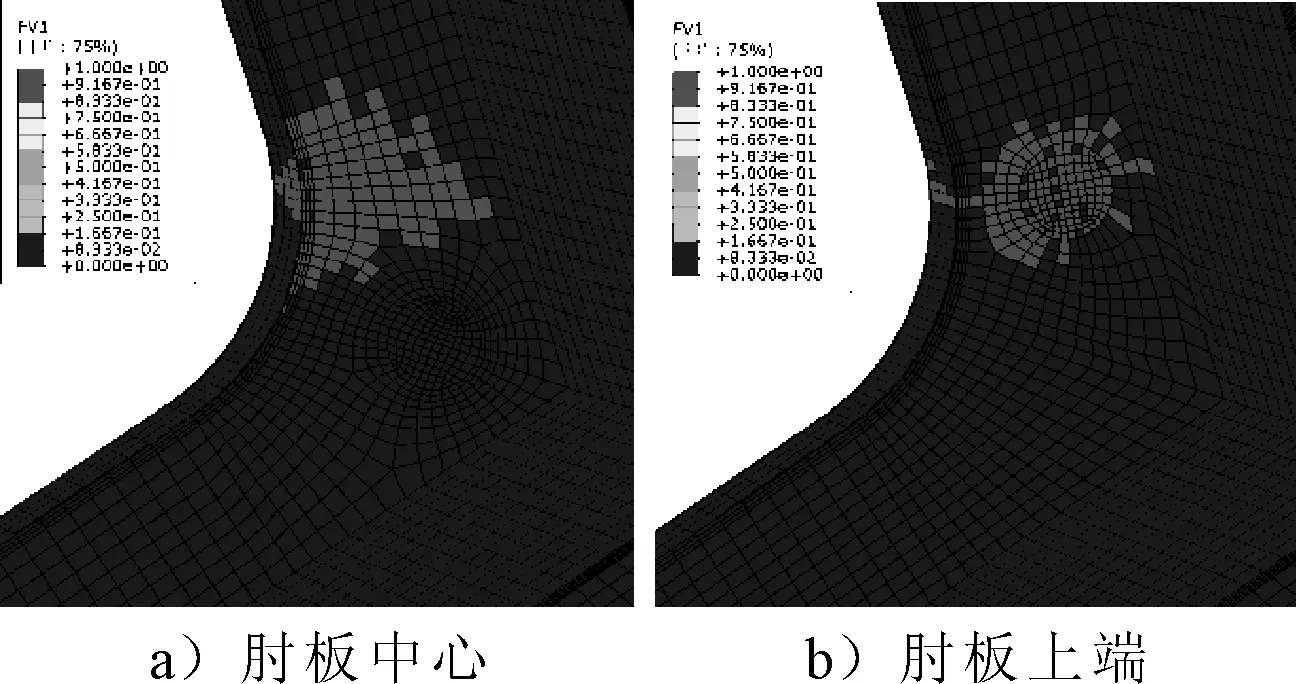
图8 含有脱粘损伤的L形节点纤维失效

kN

对比图8和图5c)，初始的脱粘损伤基本没有影响L形节点最终的失效模式和失效位置，仅肘板中心含有脱粘损伤时，1方向纤维断裂失效沿着圆弧肘板向下扩展。由表4可见，存在于肘板中心的脱粘损伤影响了胶层失效(SDEG)，使得胶层失效载荷降低，因为脱粘损伤是从肘板中心处开始发生，初始脱粘损伤加速了这一过程，但由于圆弧肘板中心本身抗弯模量较大，损伤引起的胶层失效并没有立即降低节点的承载能力。当胶层损伤扩展到一定阶段后，L形节点的承载能力才开始下降。肘板上端是截面开始变化的位置，更加容易破坏。在肘板上端存在初始脱粘损伤时，影响了圆弧肘板处的载荷传递，使得复合材料面板独立承担载荷，导致纤维破坏提前，因此，对L形节点的极限承载力影响更大。

4.2 脱粘损伤尺寸对极限承载力的影响

改变初始脱粘损伤的半径，分别计算半径为10、15、25和30 mm的圆形脱粘损伤的节点载压缩载荷下的极限承载力，计算结果见图9。图9中FV1为纤维失效，SDEG为胶层失效。

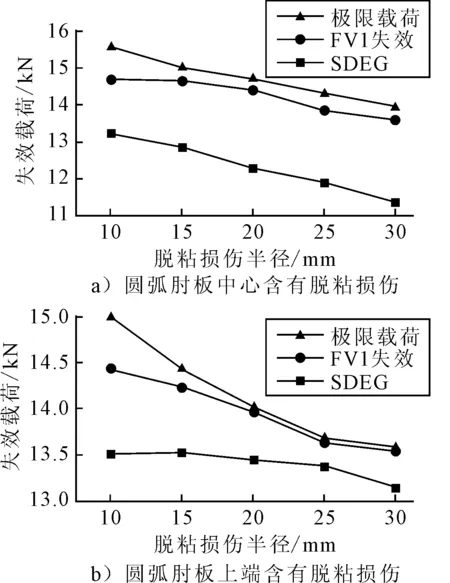
图9 失效载荷随脱粘损伤半径变化

由图9可见，随着脱粘损伤半径的增大，胶层失效载荷降低，纤维失效载荷随之降低。受二者影响，L形节点压缩载荷下的极限承载力呈下降趋势，位于肘板上端的脱粘损伤对极限承载力的影响更加明显。

对比图9a)和图9b)，当脱粘损伤位于肘板中心时，随着脱粘损伤半径增大，胶层失效载荷降低速度更快，但是纤维失效载荷和极限承载力的降低速度较慢，并且图9a)中SDEG失效的曲线与FV1失效曲线的纵向距离基本不变。这是由于胶层界面失效是从肘板中心位置开始发生，初始的脱粘损伤加剧界面失效，当胶层失效扩展引起肘板上端应力增大时，才会降低纤维失效载荷，进而降低节点的极限承载力。

脱粘损伤位于肘板上端时，胶层失效载荷降低速度较慢，而纤维失效和极限承载力降低较快，这是由于圆弧肘板上端本身应力水平更高，位于肘板上端的脱粘损伤使得纤维面板和夹芯相互独立，使其更容易破坏；随着脱粘半径增大，极限载荷曲线和FV1失效曲线之间的纵向距离逐渐减小，当半径大于20 mm时，纤维失效和L形节点的最终失效几乎同时发生，表明肘板上端脱粘失效扩大到一定程度时，失去夹芯支持的复合材料面板在发生初始失效以后几乎丧失了承载能力。

5 结论

1)采用改进的Hashin失效准则能够对夹芯复合材料L形节点在压缩载荷下的极限承载力进行较为合理的预测，为L形节点在船舶结构中的应用提供设计指导。

2)肘板上端的脱粘损伤对L形节点在压缩载荷下的极限承载力的影响大于肘板中心。随着半径增大，肘板上端的脱粘损伤的影响更加明显。当肘板上端的损伤半径大于20 mm时，L形节点在压缩载荷作用下纤维发生初始失效后会失去继续承载能力，对结构的安全性形成较大隐患，需要立即采取修复和加强措施。