改进的Holtrop船舶阻力估算

(南通中远海运川崎船舶工程有限公司，江苏 南通 226005)

目前，船舶阻力预报最精确的方法主要是船模试验，船舶设计初期，在没有型线的前提下，无法应用船模试验和CFD仿真来确定阻力，一般采用近似的方法估算船舶阻力。近似估算阻力的方法有很多，这些估算方法虽然有着耗时少，成本低等优点，但是存在估算精度低，适用范围有限等不足。改进的方法[1-5]虽探讨了不同阻力估算公式，但适用范围有限。为此，考虑从船舶设计者角度，寻求一种快速的、精度高的，以及适用范围广的预报方法。搜集30多艘三大主力船型的资料，形成船型数据库。采用Holtrop方法分别对船型数据库中的散货船、集装箱船、油船的阻力进行估算，通过数学统计分析，改进相关参数的经验公式，提出一种输入参数少，适用范围广以及估算精度高的阻力估算的半经验公式。

1 Holtrop阻力估算公式

Holtrop法[6-7]其估算公式如下。

Rt=Rf(1+k)+Rapp+Rw+Rb+Rtr+Ra(1)

式中：Rf为摩擦阻力，根据ITTC1957公式得到；1+k为船舶形状因子；Rapp为船舶附体阻力；Rw为兴波阻力；Rb为球鼻艏引起的附加阻力；Rtr为方艉引起的附加阻力；Ra为船模与实船相关的修正因子。

Holtrop给出了式(1)中每个参数的回归公式，综合这些回归公式，可以总结出其总阻力的一般函数表达式。

Rt=f(L,B,T,Δ,Cb，Cp，Cm，Lcb，ABT，hB，AT，SApp)

(2)

式中：L、B、T分别为船长、船宽、吃水；Δ为船舶的排水量；Cb、Cp、Cm分别为方形系数、棱形系数以及中横剖面系数；Lcb为船舶浮心纵向位置；ABT、hB分别为球鼻艏横向面积和球鼻艏横截面中心高度；AT为艉封板浸水面积；SApp为附体湿表面积。

采用Holtrop公式对船型数据库中的船舶进行阻力估算，并与试验值进行对比，误差分布见图1。

图1 三大主力船型Holtrop法阻力估算误差分布

由图1可见，Holtrop法估算船舶阻力的误差较大，大部分在10%～30%之内。其中散货船和肥大型油船的阻力误差相对较小，部分误差在10%以下；集装箱船的阻力误差较大，基本在15%以上。从航速上来看，速度较低时，阻力误差相对较小，当速度增加时，阻力误差随之增大。

2 改进Holtrop阻力估算公式

Holtrop公式采用三因次法估算船舶的阻力，除了黏性阻力和兴波阻力外，还考虑了球鼻艏、方尾、附体引起的附加阻力以及船模与实船的尺度效应，输入变量较多，对于不同船型，其阻力估算的误差有一定的差别。在船舶设计初期，已知的主要参数有限，尤其是球鼻艏、方尾以及附体的参数无从得知，很难利用公式进行估算。鉴于此，分别对球鼻艏、方尾以及附体引起的附加阻力进行讨论，在保证精度的前提下，寻求一种可靠的替代方案。

1)球鼻艏引起的附加阻力Rb。采用球鼻艏对于某些船型可以有效降低船舶的兴波阻力，这部分的阻力变化在兴波阻力中已经考虑，而由球鼻艏本身引起的附加阻力较球鼻艏减阻效果为小量，可放到船模与实船的修正因子Ca中考虑。另外，Holtrop公式中也对球艏重心高度作了限制，不能超出0.6Tf(艏吃水)，而球艏的重心普遍较高，限制了Rb的计算。

2)方艉引起的附加阻力Rtr。对于低速船，方艉处会形成漩涡，对阻力不利，这方面的影响可在船舶形状因子K中考虑；对于中高速船，方艉会增加船舶的虚长度，一定程度上将降低船舶的阻力，这方面的影响可在船模与实船的修正因子Ca中考虑。

3)附体阻力Rapp。附体对阻力的影响为小量，主要影响船舶的推进性能，因此，附体对阻力的影响可在船模与实船的修正因子Ca中考虑。

综合上述分析，对Holtrop公式进行一定的简化，将球鼻艏、方艉,以及附体阻力的影响考虑到船模与实船的修正因子中，得到船舶总阻力系数为

Ct=Cf(1+K)+Cw+Ca

(3)

式中：Cf为摩擦阻力系数，采用ITTC1957公式；Cw为兴波阻力系数；K为船舶形状因子；Ca为船模与实船的修正因子。

主要输入参数见表1。

表1 主要的船型参数

注：在船舶设计初期，不考虑有纵倾的工况；海水密度取常数，即1.025 kg/m3。

式(2)中的方形系数、棱形系数和中横剖面系数，采用表1中已知的参数计算得到。其中中横剖面系数Cm，可以考虑扣除中横剖面处舭部圆弧(一般圆弧半径为1.8 m)的面积近似估算得到。

Holtrop公式中没有涉及对浮心纵向位置Lcb的估算，Lcb的值对摩擦阻力的影响较小，但是其值会影响船体的艏部和艉部形状，进而影响船舶的兴波阻力和黏压阻力。根据已有船型数据库，总结Lcb与Cb的关系，见图2。

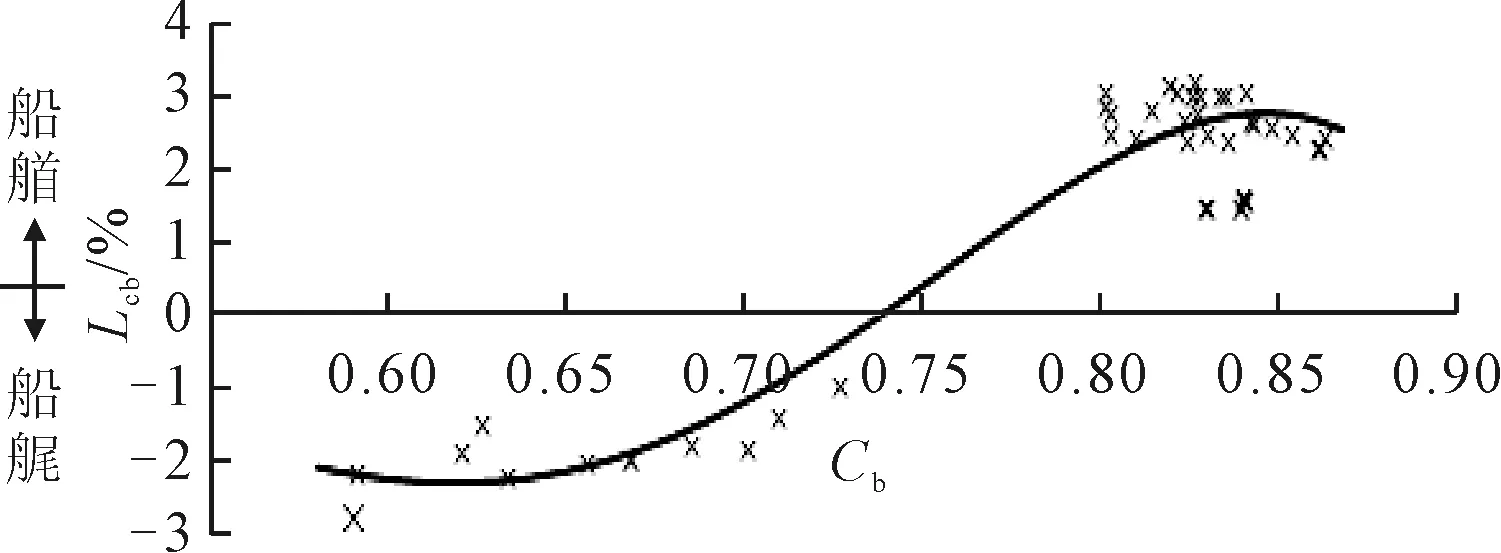
图2 浮心纵向位置随方形系数变化规律

根据图2，拟合Lcb的估算公式如下。

2 563.3Cb-387.63

(4)

Holtrop公式中给出的湿表面积公式如下。

0.286 2Cm-0.003 467B/T+

0.369 6Cwp)+2.38ABT/Cb

(5)

对数据库中的数据进行拟合，在式(5)的基础上进行修改，得到湿表面积估算公式如下。

Smod=L(2T+B)(0.623 5+0.333 2Cb-

0.002 611B/T)+BL(0.264 1Cb-0.261 3)

(6)

运用式(5)和式(6)估算数据库中三种主力船型的湿表面积，并与实际值进行对比，见图3。

图3 两种方法估算不同船型湿表面积误差对比

由图3可见，由式(6)估算得到的湿表面积的误差明显降低。

对于形状因子，Holtrop方法中给出了1+K的估算公式。

1+K=0.93+0.487 118c14(B/L)1.068 06·

(T/L)0.461 06(L/LR)0.121 563·

(L3/▽)0.364 86(1-Cp)-0.604 247

(7)

式中：LR为Holtrop公式中定义的船型因子，与L、Cp、Lcb有关。运用式(7)对现有船型的形状因子进行估算，并与数据库中的数据进行对比。通过分析对比，修改式(7)，得到改正后的形状因子公式如下。

1+Kmod=1.046 6+0.312(B/L)1.068 06·

(T/L)0.461 06(L/LR)0.121 563·

(L3/▽)0.364 86(1-Cp)-0.604 247

(8)

兴波阻力估算仍采用Holtrop法中给出的公式。式(3)中并未单独考虑球艏、方尾、附体等的影响，而是将这些影响放到了船模与实船的修正因子Ca中。通过对比改进后的经验公式和船型数据库中船舶试验结果，发现Ca的值不仅与船长和船速有关，还与船型有关。根据水池试验的结果和式(3)，回归分析得到不同船型修正因子Ca的关系。

1)集装箱船(R2=0.83)。

Ca×103=-0.434 2-13.61Fr2+

1.858Fr+125.6/L

(9)

2)散货船(R2=0.71)。

Ca×103=0.256 1-26.06Fr2+

0.800 6Fr+47.95/L

(10)

3)油船(R2=0.69)。

Ca×103=-1.482-65.07Fr2+

18.11Fr+109.9/L

(11)

式中：Fr为弗劳德数；R2为回归系数，表示模型拟合度的好坏，其值越接近1，说明拟合效果越好，从回归系数可以看出，回归公式的拟合度较好。

3 改进的船舶阻力公式验证

为进一步验证上述公式的精度及适用性，以不属于船型数据库中的3艘主力船为例，采用上述改进的半经验公式进行估算船舶的阻力。3艘船的主要参数见表2。估算结果见表3～5。

表2 三种主力船型基本参数

表3 集装箱船阻力估算值与试验值对比

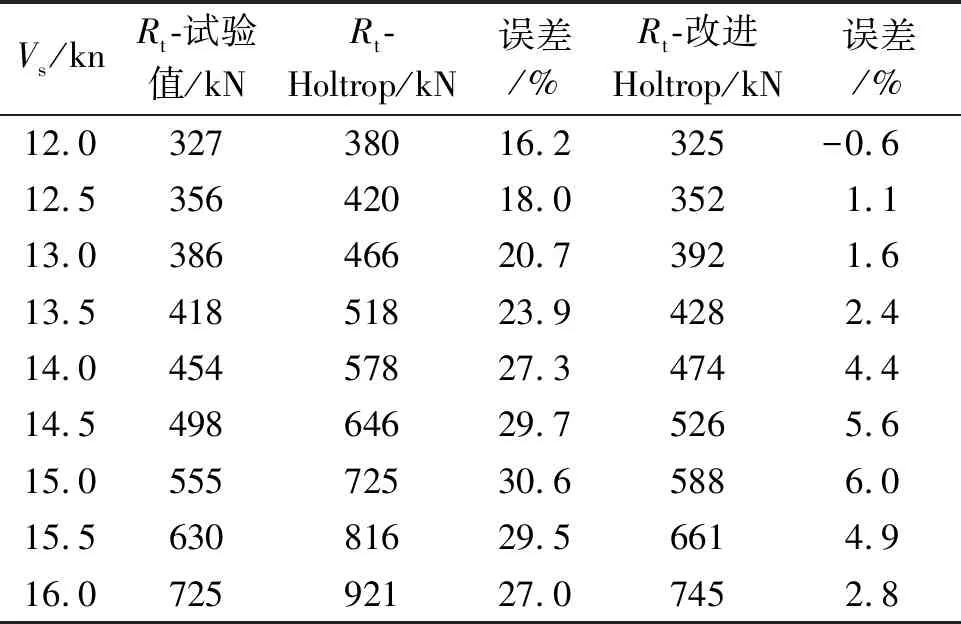
表4 散货船阻力估算值与试验值对比

表5 油船阻力估算值与试验值对比

由表3～5可见，改进后的Holtrop法估算结果对3种主力船型都有很好的适用性，并且误差也得到改善，均在7.0%以内，达到一定的修正效果。

4 结论

通过对比现有新造船的船型数据库，基于三大主力船型的试验数据，对Holtrop法中部分公式进行改进，修正船模与实船相关因子，并减少该方法的输入参数。经过验证，采用改进的方法，3种船型的阻力估算值的精度明显得到提高，具有一定的工程应用价值。

将已有的估算公式与已建造船的数据结合起来，通过总结和归纳的方法，寻求适合新造船阻力估算的方法，在船舶设计初期不失为一种有效的阻力估算方法。鉴于本文的船型数据库样本容量有限，统计公式仍需进一步完善。另外，本文仅分析了阻力的估算方法，对推进方面的归纳还需进一步探讨。