基于Prony-Iike方法的第一类贝塞尔函数逼近

纪宇　何一璇　吴国群　吴敏

摘要：贝塞尔函数的数值逼近既有重要的理论意义，又在数学、物理学、工程等各个领域有着广泛的应用.研究整数阶第一类贝塞尔函数的数值逼近，基于Prony方法，采用不同三角函数（正弦、余弦）形式的Prony-like方法进行逼近.通过在符号计算软件Maple中对函数进行数值实验，分析不同整数阶的第一类贝塞尔函数在不同自变量区间上的数值逼近，将Prony-like方法的实验结果与基于傅里叶级数展开的方法进行对比，发现Prony-like方法的逼近效果远优于基于傅里叶级数的方法.

关键词：贝塞尔函数;Prony-like方法;三角函数;基于傅里叶级数展开;数值逼近

中图分类号：TP311.5

文献标志码：A

DOI： 10.3969/j.issn.1000-5641.2019.06.006

0 引言

特殊函数是指一些具有特定性质的函数，它们广泛应用于物理学、化学、工程、统计学以及计算机科学等领域，大多数特殊函数都没有闭形式的表达式，其赋值只能通过数值逼近来实现.由于特殊函数在应用中的重要性和广泛性，因此，如何提高数值逼近的效率，具有重要的学术意义和应用价值.

有关特殊函数的性质和数值计算方法，众多国内外学者作出了大量的研究.1964年，Abramowitz、Stegun和Romain在文献[1]中详细介绍了特殊函数的定义、性质、数值逼近方法.2010年，美国国际标准与技术研究院（NIST）发布了NIST数学函数数字图书馆（Digital Library of Mathematical Functions，DLMF）[2]，系統地介绍了特殊函数的性质和常用赋值方法.

贝塞尔函数（Bessel functions）是德国数学家贝塞尔于1817年研究三体引力系统的运动问题时提出的，贝塞尔函数在波的传播、有势场和信号处理领域有着广泛的应用，如圆柱形波导中的电磁波传播、调频合成等.

贝塞尔函数是一类特殊函数，无法由初等函数直接表示.针对贝塞尔函数的数值逼近，已有的研究提出了许多数值方法[1-2].文献[3]对整数阶和半整数阶第一类贝塞尔函数的幂级数、渐近级数和连分式展开进行了比较.文献[4]对任意整数阶的贝塞尔函数讨论了多项式逼近.文献[5]提出了基于泰勒级数展开、Debye渐近展开和Sommerfeld积分的算法，对贝塞尔函数进行逼近.

在之前的工作中，幂级数、渐近级数展开等数值方法对整数阶第一类贝塞尔函数的逼近效率不高，且在数值上不稳定.我们注意到贝塞尔函数表现出近似周期性的性质，因此，在本文中，针对贝塞尔函数的这一性质，考虑通过三角函数的和形式（∑墨，ai cos（cpix）或∑n：lai sin（cpix））对贝塞尔函数进行逼近.

基于傅里叶级数的方法是基于这种思路的一种应用.傅里叶级数在理论、数学和工程领域都有着重要的研究价值.傅里叶级数方法是把类似波的函数表示成简单正弦波的和，它把任何周期函数或周期信号分解成简单震荡函数（如正弦函数和余弦函数）的集合.在文献[6]中，提出了利用傅里叶级数展开对贝塞尔函数进行逼近，然而，正如本文实验所示，形式为ai cos（kx）和ai sin（kx）的和的逼近效果并不理想.

我们转而考虑另一种三角函数形式的逼近方法.Prony方法作为傅里叶级数的一种拓展，最早由Prony在1795年提出[7].Prony方法通过在一个均匀采样的样本中提取有用的信息，并建立一系列的衰减指数或正弦函数.Prony方法常作为一种线谱估计方法应用于各领域的信号处理.但Prony模型在数值上是病态的，非最优、非严格的近似求解算法，对噪音的干扰非常敏感，这极大地限制了Prony模型的应用.Prony方法的复兴起源于对Prony方法的修改，这显著稳定了原始方法，例如，ESPRIT方法，矩阵束方法或近似Prony方法[8-11].近年来，Prony方法也已经成功应用于不同的逆问题，如，量子化学[12]或流体动力学[13]中Green函数的近似，反向散射中粒子的定位[14]等.

本文中，我们针对整数阶第一类贝塞尔函数，基于扩展形式的Prony方法，采用三角函数和的形式对第一类贝塞尔函数进行逼近，并将实验结果与基于傅里叶级数方法的实验结果作比较.

本文第1节介绍了第一类贝塞尔函数的定义和相关性质;第2节介绍了贝塞尔函数的基于傅里叶级数展开形式;第3节和第4节分别介绍了指数形式的Prony方法和三角函数形式的Prony-like方法;第5节分别应用基于傅里叶级数方法和Prony-like方法对第一类贝塞尔函数进行数值逼近，并比较两种方法的逼近效果，

本文中，R、Z、C分别表示实数集、整数集和复数集.

1 第一类贝塞尔函数

然而，上述Prony方法中的多项式求根问题在数值上是病态的，非最优、非严格的近似求解算法对噪音的干扰非常敏感，这极大地限制了Prony方法的应用.1999年，Golub等提出Prony方法的一种重要表述，将求解Hankel系统和求解生成多项式的根的问题转化为求解一个广义特征值问题[15].广义特征值问题一般可通过Cholesky分解和LU分解来有效求解，存在成熟的且数值稳定的数值方法，因此，这一新表示使Prony方法的应用得以复兴.

下面，我们来简单介绍一下基于广义特征值问题表述的Prony方法.

给定正实数b和区间|a，b|上的实函数f（x），计算如下形式的展开式：

Prony方法可以把求解ai、φi的非线性问题转化为求解两个线性方程组的问题，即广义特征值问题和含范德蒙矩阵的线性方程组问题.

5 基于傅里叶级数方法与Prony-like方法的实验结果对比

在本节中，我们用基于傅里叶级数的方法和Prony-like方法对J（y;b）进行函数逼近，并比较其逼近结果.为使计算精度尽可能高，所有实验均在计算机代数软件Maple中进行.我们通过设置Digits，来保证实验结果的精度.

5.1 J0（y;b）和J1（y;b）

由J0（Y）和J1（y）的奇偶性以及知，JO （y;b）和J1（y;b）是偶函数.所以应用4.1节中的cosine形式的Prony-like方法在区间[O，b]上对Jo（Y）、J1（y）进行数值逼近，并与基于傅里叶级数的方法进行比较.为比较两种方法的逼近效果，我们在区间[0，b]上按照1/2 10的间隔取样本点，并计算出Prony-like方法和基于傅里叶级数方法在这些样本点的相对误差.为简便起见，我们取相对误差的对数值（log10）.

（1）J0（y;b）

在n=0，b=1时，分别用基于傅里叶级数方法和Prony-like方法对J0（y;1）进行了数值逼近.

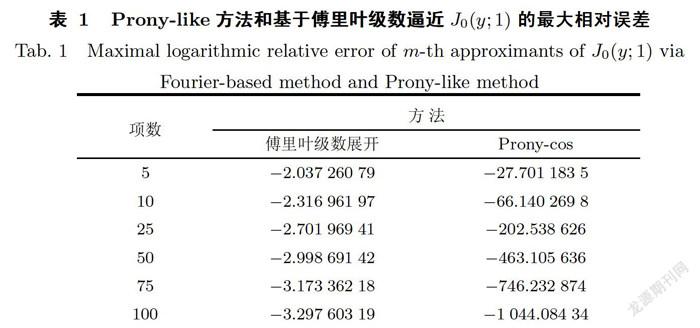
表1展示了JO （y;1）在6=l，即自变量区间为[O，1l时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，10，25，50，75，100时的最大相对误差（l09io）.

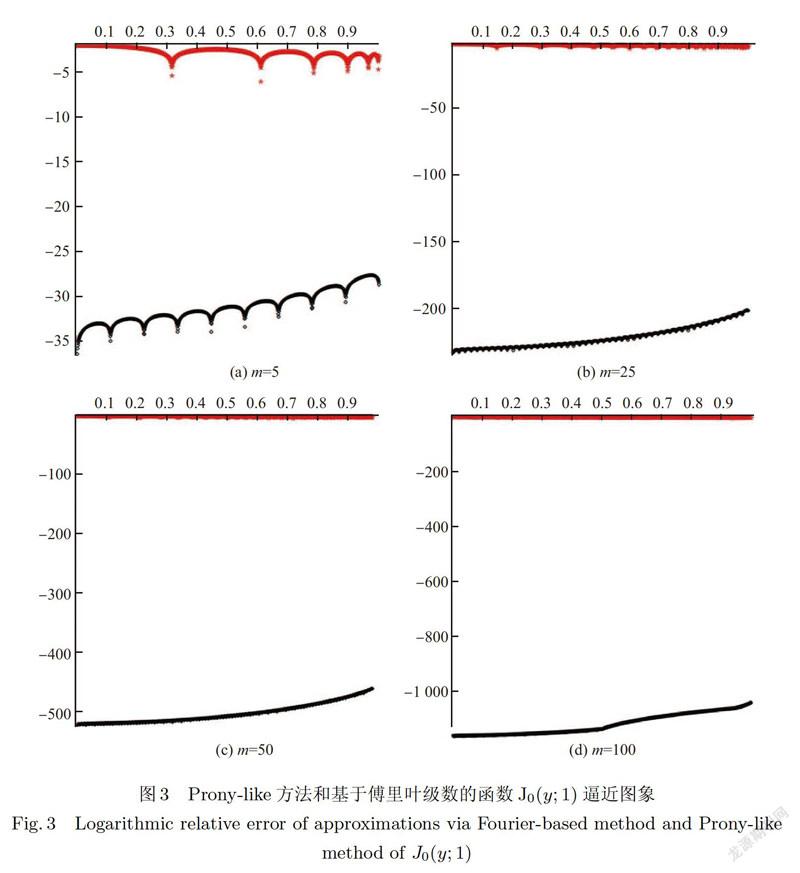
图3分别展示了Jo（Y;1）在自变量区间[0，1]上，基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10），其中横坐标表示自变量x的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

设6为正实数，我们分别用基于傅里叶级数的方法和Prony-like方法对JO （y;b）进行了数值逼近.

表2和表3分别展示了JO （y;b）在b=5和b=20，即在区间[0，5]和[0，20]上，基于傅里叶级数方法和Prony-like方法在展开项数m=5，10，25，50，75，100时的最大相对误差（log10）.

图4展示了JO （y;b）在区间为[0，5]时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10）.其中，横坐标表示自变量x的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

从表1、表2、表3及图3、图4中可以看出，Prony-like方法的最大相对误差远小于基于傅里葉级数的方法，且相对误差随展开项数的增大而效果更好.结合JO （y;1）的图象，发现相对误差随取值范围[0，b]增大而增大，且相对误差随展开项数的增大而变好.若想获得与JO （y;1）同样的逼近效果，需要更大的展开项数.

（2）J1（y;b）

在n=l，b=l时，分别用基于傅里叶级数方法和Prony-like方法对J1（y;1）进行数值逼近.

表4展示了Jl（y;1）在6=1，即自变量区间为[0，1]时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，10，25，50，75，100时的最大相对误差（l09io）.

图5展示了J1（y;1）在自变量区间为[0，1]时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10）.其中，横坐标表示自变量x的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

在n=l，b>l时，我们分别用基于傅里叶级数方法和Pronv-like方法对J1（y;b）进行了数值逼近，

表5、表6展示了J1（y;b）在b=5和b=20，即区间为[0，5]和[0，20]时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，10，25，50，75，100时的最大相对误差（log10）.

图6给出了在区间[0，5]上，J1 （y;b）基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10）.其中，横坐标表示自变量x的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

从表4、表5、表6及图5、图6中可以看出，类似于JO （y;b），J1（y;b）的Prony-like方法的最大相对误差远小于基于傅里叶级数方法，且相对误差随展开项数的增大而效果更好.结合J1（y;1）的图象，发现相对误差随展开项数的增大而变好，但同时相对误差随取值范围[0，b]的增大而增大.因而，为了获得与J1（y;1）同样的逼近效果，需要展开更多的项数.

5.2

J2 （y;b）

由于J2（x）是偶函数，因而J2（y;b）=J2（y）/ y/b是奇函数，我们应用基于傅里叶级数方法和4.2节介绍的sine形式的Prony-like方法在区间[0，b]上对J2 （y;b）进行数值逼近.

令b= 1.我们分别用基于傅里叶级数方法和Prony-like方法对J2 （y;1）进行数值逼近.

表7展示了J2 （y;1）在自变量区间为[0，1]时，基于傅里叶级数方法和Prony-like方法在展

图7分别展示了J2（y;1）在自变量区间[O，1]上，基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10）.其中，横坐标表示自变量x的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

以下，设b>l，分别应用基于傅里叶级数方法和Prony-like方法对J2 （y;b）进行了数值逼近，

表8和表9展示了J2 （y;b）在b=5和b=20，即区间为[0）5]和[O，20]时，基于傅里叶级数方法和Prony-like方法在展开项数m=5，10，25，50，75，100时的最大相对误差（log10）.

图8展示了J2 （y;b）在区间[0，5]上，基于傅里叶级数方法和Prony-like方法在展开项数m=5，25，50，100时的相对误差（log10）.其中，横坐标表示自变量z的值，纵坐标表示相对误差对数值，红色曲线和黑色曲线分别代表基于傅里叶级数方法和Prony-like方法的相对误差.

从表7、表8、表9及图7、图8中可以看出，J2 （y;b）与JO （y;b）、J1（y;b）的实验结果相似，即Prony-like方法的逼近效果远优于基于傅里叶级数的方法.5.3基于傅里叶级数方法与Prony-like方法计算时间对比

本小节以函数JO （y;b）、J1（y;b）和J2 （y;b）的逼近为例，比较基于傅里叶级数的方法和Prony-like方法在不同展开项数和不同区间下的计算时间.表10给出了比较结果.

从表10可以看出，基于傅里叶级数方法的计算时间比Prony-like方法的计算时间短，旦随着展开项数的增加，两种方法计算时间的差距逐渐拉大，两种方法受自变量区间和阶数影响均不大.然而，Prony-like方法可以在项数很小时得到非常高的精度，如J0 （y;1）在展开5项时，Prony-like方法比基于傅里叶级数方法的精度高约10，计算时间仅长0.154 s，所以Prony-like方法逼近效果更好.

6 结语

本文对整数阶第一类贝塞尔函数进行数值逼近，基于前面的分析和实验可得，cosme和slne形式Prony-like方法的数值逼近结果远远优于基于傅里叶级数方法，虽然Prony-like方法的计算时间略长于基于傅里叶级数方法的计算时间，但是Prony-like方法可以在项数很小时就得到很高的精度，所以Prony-like方法的逼近效果更好.在未来的工作中，将针对复数阶的贝塞尔函数应用Prony-like方法进行实验.作为Prony-like方法的改进，下一步的研究将侧重于改进通过 Hankel矩阵和广义特征值问J题求解φi的复杂计算过程，进一步提高 -角函数和形式的计算

[参考文献]

[1]ABRAMOWITZ M， STEGUN I A， ROMAIN J E. Handbook of Mathematical Functions with Formulas， Graphs：nd Mathematical Tables [M]. New York： Dover， 1964.

[2] LOZIER D W. NIST Digital library of mathematical functions [J]. Annals of Mathematics & Artificial Intelli-gence： 2003， 38（1/3）： 105-119.

[3] 常曉阳. JL类特V殊函数的赋值分析研究 [D] .上海：华东师范大学， 2018.

[4]MILLANE R P， EADS J L. Polynomial approximations to Bessel functions [J]. IEEE Transactions on Antennas& Propagation， 2003， 51（1）： 1398-1400.

[5] MATVIYENKO G. On the evaluation of Bessel functions [J]. Applied and Computational Harmonic Analysis，1993， 1（1）： 116-135.

[6]ANDRUSYK A. Infinite series representations for Bessel functions of the first kind of integer order [EB/OLl.[2018-10-20]. https：//arxiv.org/abs/1210.2109

[7]HILDEBRAND F B. Introduction to Numerical Analysis [M] . New Delhi： Tata McGraw-Hill Publishing Company Limited， 1956.

[8]B013MANN F， PLONKA G， PETER T， et al. Sparse deconvolution methods for ultrasonic NDT [J]. Journal ofNondestructive Evaluation， 2012， 31（3）： 225-244.

[9]ROY R， PAULRAJ A. KAILATH T. Estimation of signal parameters via rotational invariance techniques-ESPRIT [C]// Proceedings of the SPIE. International Society for Optics and Photonics， 1986： 94-101.

[10] HUA Y： SARKAR T K. Matrix pencil method for estimating parameters of exponentially damped/undampedsinusoids in noise [J]. IEEE Transactions on Acoustics， Speech， and Signal Processing， 1990， 38（5）： 814-824.

[11] POTTS D， TASCHE M. Nonlinear approximation by sums of nonincreasing exponentials [J] . Applicable Analysis：2011， 90（3/4）： 18.

[12] YANAI T， FANN G I， GAN Z. et al. Multiresolution quantum chemistry in multiwavelet bases： Analyticderivatives for Hartree-Fock and density functional theory [J] . Journal of Chemical Physics： 2004， 121（7） ： 2866-2876.

[13] BEYLKIN G， CRAMER R， FANN G， et al. Multiresolution separated representations of singular and weaklysingular operators [J] Applied & Computational Harmonic Analysis， 2007， 23（2）： 235-253.

[14]HANKE M. One shot inverse scattering via rational approximation [J]. Siam Journal on Imaging Sciences： 2012，5（1）： 465-482.

[15] GOLUB G H， MILANFAR P， VARAH J. A Stable Numerical Method for Inverting Shape from Moments [M].Society for Industrial and Applied Mathematics： 1999.

[16] GIESBRECHT M， LABAHN G， LEE W S. Symbolic-numeric sparse polynomial interpolation in Chebyshevbasis and trigonometric interpolation [C]// Proceedings of Computer Algebra in Scientific Computing （CASC2004） ， 2004： 195206.

[17]CUYT A. LEE W S. Generalized eigenvalue relations： Spread polynomials and sine [R]. 2018.

（責任编辑：林磊）

收稿日期：2018-11-30

基金项目：国家自然科学基金（11371143）

第一作者：纪宇，女，硕士研究生，研究方向为数值计算、符号计算.E-mail： 15526476747@163.com.

通信作者：吴敏，女，副教授，主要研究方向为符号计算、数值计算.E-mail： mwu@sei.ecnu.edu.cn.