一种求解位移方程组问题的加权简化广义最小残量算法

仲红秀　杨书恒

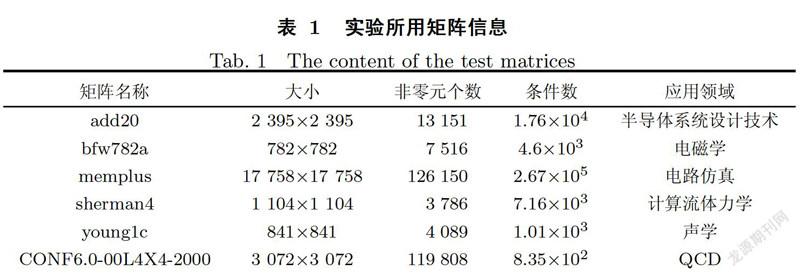
摘要：结合加权策略和简化的广义最小残量算法（GMRES），提出可有效求解位移线性方程组的加权简化GMRES算法，并给出加权简化GMRES算法与简化GMRES算法之间的联系与性质，最后数值算例给出了新算法的有效性.

关键词：位移方程组; 简化GMRES; 加权矩阵

中图分类号：0241.6

文献标志码：A

DOI： 10.3969/j.issn.1000-5641.2019.06.004

0 引言

本文主要研究如下大型位移线性方程组的求解：

收稿日期：2018-06-12

基金项目：国家自然科学基金（11701225）;江苏省自然科学基金（BK20170173）

第一作者：仲红秀，女，博士，讲师，研究方向为数值线性代数.E-mail： hxzhong@jiangnan.edu.cn.称（2）为种子系统，（3）为额外系统，位移方程组问题常见于科学与工程计算的应用领域，如结构动力学[1]，量子色动力学（QCD）[2]，网页搜索[3]，控制论[4]等等，因此，探索求解位移方程组的有效数值解法具有重要的理论意义与实际意义.

由于Krylov子空间方法具有位移不变性，即：

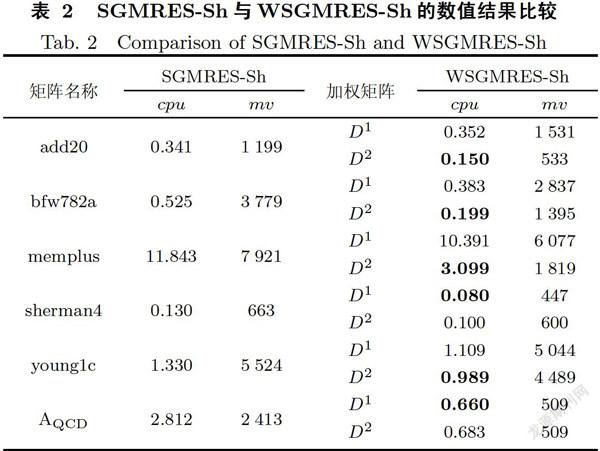
表2列出了WSGMRES-Sh和SGMRES-Sh的数值结果，其中mv表示矩阵A与向量的乘积个数，cpu表示CPU时间（单位：s），表中的黑体数值表示消耗CPU时间最少的数值.从表中可见，除了矩阵sherman4，当加权矩阵选取D2时，WSGMRES-Sh所消耗的矩阵向量积比SGMRES-Sh少很多，收敛速度比SGMRES-Sh快.因此整体来说，WSGMRES-Sh比SGMRES-Sh更优.但是因为D-内积需要消耗更多的时间，且加权矩阵D-的取法也会影响收敛速度，最优的D的选取方法还有待进一步的研究.

[参考文献]

[1]SIMONCINI V， PEROTTI F. On the numerical solution of （A2A + AB + C）x = b and application to structualdynamics [J] SIAM J Sci Comput， 2002， 23（6）： 1876-1898.

[2] DARNELL D， MORGAN R B， WILCOX W. Deflation of eigenvalues for iterative methods in lattice QCD [J]. Nucl Phys BProceedings Supplements， 2004， 129/130： 856-858.

[3]LANGVILLE A N， MEYER C D. Google's PageRank and Beyond： The Science of Search Engine Rankings [M].Princeton： Princeton University Press， 2006.

[4]AHMAD M I， SZYLD D B， VAN GIJZEN M B. Preconditioned multishift BiCG for H2-optimal model reduction[J]. SIAM J Matrix Anal Appl， 2017， 38（2）： 401-424.

[5]WALKER H， ZHOU L. A simpler GMRES [J]. Numer Linear Algebra Appl， 1994， 1（6）： 571-581.

[6]JING Y F. YUAN P， HUANG T Z. A simpler GMRES and its adaptive variant for shifted linear systems [J] Numer， Linear Algebra Appl， 2017， 24（1）： 1-7.

[7] 楊圣炜，卢琳璋. -种加权VJ Simpler GMRES算法 [J]厦门大学学报 （自然科学版）， 2008（4）： 484-488.

[8]CAO Z H， YU X Y. A note on weighted FOM and GMRES for solving nonsymmetric linear systems [Jl Appl Math Comput， 2004， 151： 719-727.

[9]ZHONG H X. WU G. Thick restarting the weighted harmonic Arnoldi algorithm for large interior eigenproblems[J]. Int J Comput Math， 2011， 88（5）： 994-1012.