非线性高维扰动Klein-Gordon方程的孤子波摄动解

徐建中　莫嘉琪

摘要：利用广义变分迭代方法讨论了一类非线性强迫扰动Klein-Gordon方程.首先，用双曲函数待定系数法求得了无扰动方程孤子波.其次，利用泛函变分迭代原理得到了强迫扰动Klein-Gordon方程的一个摄动近似解.最后，论述了解的一致有效性.得到的近似解是解析式，它可对近似解进行解析运算，这对用简单的模拟方法得到的近似解是达不到的.

关键词：摄动解;孤子波;变分迭代

中图分类号：0157.29

文献标志码：A

DOI： 10.3969/j.issn.1000-5641. 2019.06.003

0 引言

非线性孤子波理论在地球物理、光学、力学、理论物理学等学科中有很重要的应用.例如在地理科学、海洋物理、散射波、燃烧理论等方面，许多学者作了多方面的研究，如Salathiel等利用Riccati方程映射方法研究了电晶格孤子行波[1]，Yu等研究了Bose-Einstein冷凝体的孤子波[2]、 Chow等研究了K-折叠松散的Ricci孤子波[3]，等等[4-9].非线性孤子波理论的定量和定性方法已有很多的改进，非线性孤子波解的一种研究方法是扰动理论的近似方法，主要是用扰动理论的近似展开式将非线性孤子波方程转化为易求解的方程来求解，这样就摆脱了对于模拟数值方法的依赖.此方法的优点在于思路直接明了，计算简单，可得到解的较高近似度.且求得的近似解具有解析性态，故不但能进行定量方面的分析，而且还能进行定性方面的分析.此方法使用面广，具有较广的研究前景，

作者等人利用广义变分迭代、同伦映射、微分不等式和不动点理论等方法也研究了一些孤立波理论及有关的非线性问题[10-15].本文就是研究一类非线性高维扰动KG（Klein-Gordon）方程.对于一般较典型的KG方程已有许多研究，它代表的是许多自然现象的简化情形.但此类方程已经不完全能满足当前科学发展的要求，所以需要研究更能反映自然现象的广义非线性高维强迫扰动KG方程.

1 非线性高维扰动KG方程

考虑如下广义非线性扰动KG方程：其中a，m，k为正的常数，f为非线性强迫扰动项，它是关于其变量为足够光滑的函数.

近年来，关于非线性KG方程解的研究大体集中在兩个方面.一方面是利用分析方法求出各种方程的精确解，如He等[16]利用推广的F展开方法求得了某类发展方程的精确解，Zhang等[17]利用变形映射方法给出了方程的精确解;另一方面是定性地研究解的性态，如Zhang等[18]对KG方程给出波函数和能量方程.Teman[19]证明了一类KG方程整体吸引子的存在性.近来，典型的非线性KG方程还有许多研究，例如文献[20-22]等，但一般的典型KG方程代表的是各种自然现象的精简和浓缩，它不能满足当前科学发展的需要，故有必要来研究更能表示真实自然现象的广义扰动KG方程.显然，复杂的非线性方程一般不能求出其精确解.本文提出了一类更一般的带有非线性高维扰动KG方程（1）的求近似解方法，得到的这种近似解又可以继续进行解析分析，进而能得到更深入的物理性态。

首先作行波变换：

不失一般性.上述所列出的孤子波行波解（II）、（12），在泛函变分迭代方法下，都可作为扰动KG方程的泛函迭代式的初始近似，本文是利用式（9）作为初始近似.即u0（z）=v1（z），并以此来求出对应的各次近似解.

2 强迫扰动KG方程解的变分迭代

为了求得非线性强迫扰动KG方程（3）具有较好精度的近似解，现采用泛函分析变分迭代方法[16].作泛函F：

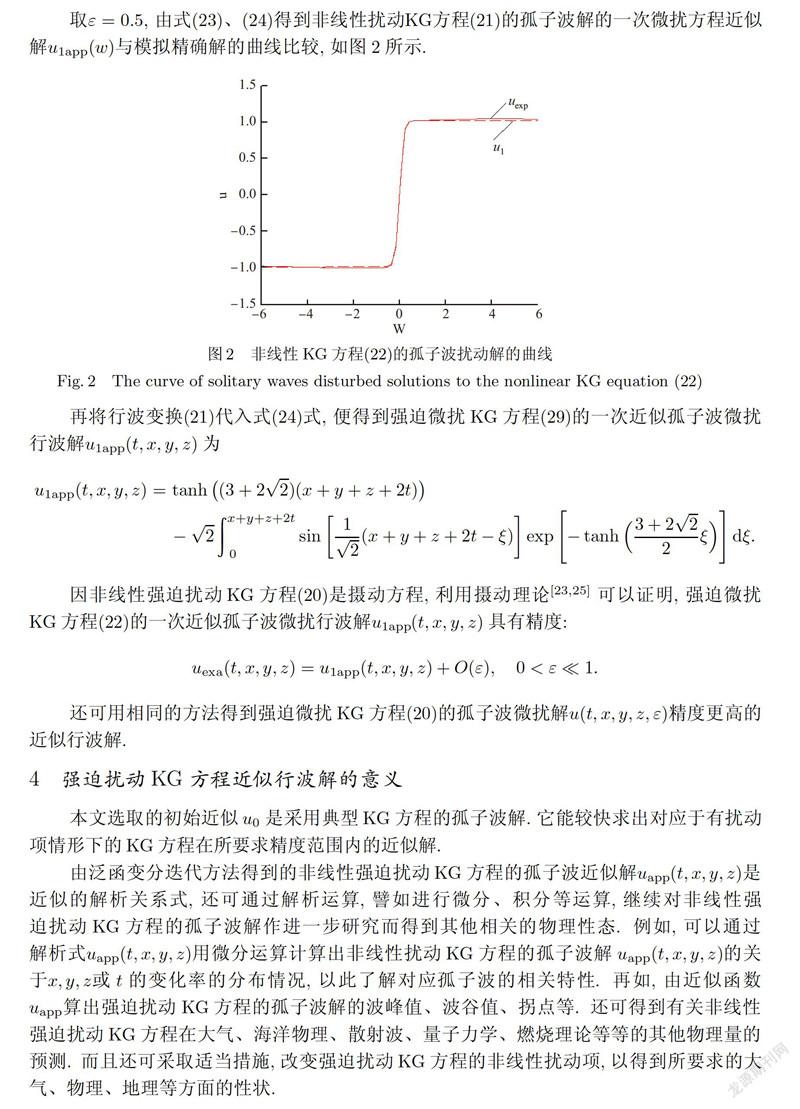
取ε= 0.5，由式（23）、（24）得到非线性扰动KG方程（21）的孤子波解的一次微扰方程近似解ulapp （w）与模拟精确解的曲线比较，如图2所示.

4 强迫扰动KG方程近似行波解的意义

本文选取的初始近似u0。是采用典型KG方程的孤子波解.它能较快求出对应于有扰动项情形下的KG方程在所要求精度范围内的近似解.

由泛函变分迭代方法得到的非线性强迫扰动KG方程的孤子波近似解uapp（t，x，y，z）是近似的解析关系式，还可通过解析运算，譬如进行微分、积分等运算，继续对非线性强迫扰动KG方程的孤子波解作进一步研究而得到其他相关的物理性态.例如，可以通过解析式uapp（t，x，y，z）用微分运算计算出非线性扰动KG方程的孤子波解uapp（t，x，y，z）的关于x，y，z或t的变化率的分布情况，以此了解对应孤子波的相关特性.再如，由近似函数u app算出强迫扰动KG方程的孤子波解的波峰值、波谷值、拐点等.还可得到有关非线性强迫扰动KG方程在大气、海洋物理、散射波、量子力学、燃烧理论等等的其他物理量的预测.而且还可采取适当措施，改变强迫扰动KG方程的非线性扰动项，以得到所要求的大气、物理、地理等方面的性状。

[参考文献]

[1] SALATHIEL Y， AMADOU Y， GARMBO B G. et al. Soliton solutions and traveling wave solutions for adiscrete electrical lattice with nonlinear dispersion through the generalized Riccati equation mapping method[J]. Nonlinear Dynamics， 2017： 87（4）： 2435-2443.

[2] YU F J，LI L.Vector dark and bright soliton wave solutions and collisions for spin-l Bose-Einstein condensate[J]. Nonlinear Dynamics， 2017， 87（4）： 2697-2713.

[3] CHOW B， LU P. On K-noncollapsed complete noncompact shrinking gradient Ricci solitons which split at infinity[J]. Math Annalen， 2016， 366（3/4）：1195-1206.

[4] SAZONOV s V. New type of extremely short vector solitons in a medium of asymmetric molecules [J]. JETPLetters， 2015， 102 （12）： 834-840.

[5] 欧阳成，姚静荪，石兰芳，等一类尘埃等离子体孤子波解[J].物理学报，2014， 63（11）：110203-110208.

[6] 石兰芳，朱敏，周先春，等.一类非线性发展方程孤立子行波解[J].物理学报，2014， 63（13）： 130201-130205.

[7] OUYANG C， CHENG L H， MO J Q. Solving a class of burning disturbed problem with shock layers [J]. ChinPhys B： 2012， 21（5）： 15-18

[8] SHI L F，CHEN c s，ZHOU x C. The extended auxiliary equation method for the KdV equation with variablecoefficients [Jl. Chin Phys B， 2011， 20（10）： 803-811.

[9] 石兰芳，周先春，一类扰动Burgers方程的孤子同伦映射解[J].物理学报，2010. 59（5）：2915-2918.

[10]MO J Q. Homotopic mapping solving method for gain fluency of a laser pulse amplifier [J]. Science in China G.2009， 39（7）： 1007-1010.

[11]MO J Q， LIN s R. The homotopic mapping solution for the solitary wave for a generalized nonlinear evolutionequation [J]. Chin Phys B， 2009， 18（9）： 3628-3631.

[12]MO J Q. Solution of travelling wave for nonlinear disturbed long-wave system [J]. Commun Theor Phys， 2011，55（3）： 387-390.

[13] MO J Q， CHEN x F. Homotopic mapping method of solitary wave solutions for generalized complex Burgersequation [J]. Chin Phys B， 2010， 19（10）： 20-23.

[14] XU J z，ZHOU z F. Existence and uniqueness of anti-periodic solutions for a kind of nonlinear nth-orderdifferential equation with multiple deviating arguments [J]. Ann Diff Eqn： 2012， 28（1）： 105-114.

[15] 徐建中，周宗福.一类四阶具有多个偏差变元p-Laplacian中立型微分方程周期解的存在性[J].重庆工商大学学报，2012.29（11）： 9-16.

[16]HE J H， WU x H. Construction of solitary solution and compaction-like solution by variational iteration method[J]. Chaos Solitons& Fractals， 2006， 29（1）： 108-113.

[17] ZHANG x A， CHEN K， DUAN z I.Bound states of KG equation and Dirac for ring-shaped non-sphericaloscillator scalar and vector potential [J]. Chin Phys， 2005： 14（1）： 42-44

[18] ZHANG Q， YUE P，GONG L X. New exact solutions of nonlinear KG equation [J]. Chin Phys： 2006， 15（1）：35-38.

[19]TEMAN R. Infinite-dimensional Dynamical System in Mechanics and Physics [Ml. 2nd ed. New York： Springer，1997.

[20] 張建文，王旦霞，吴润衡，一类广义强阻尼Sine-Gordon方程的整体解[J].物理学报，2008， 57（4）：2021-2025.

[21] 韩兆秀.非线性KG方程新的精确解[J].物理学报，2005， 54（4）： 1481-1484.

[22] 卢殿臣，杨立波，洪宝剑，非线性KG方程新的精确解[J].江苏大学学报，2010， 31（1）：120-124.

[23] CHANG K W. HOWES F A. Nonlinear Singular Perturbation Phenomena： Theory and Applications [M]. NewYork： Springer-Verlag， 1984.

[24]DE JAGER E M， JIANG F R. The Theory of Singular Perturbation [M]. Amsterdam： North-Holland PublishingCo. 1996.

[25] BARBU L，MOROSANU G. Singularly Perturbed Boundary-Value Problems [M]. Basel： Birkhauser， 2007.

（责任编辑：林磊）

收稿日期：2018-08-14

基金项目：国家自然科学基金（41275062）;安徽省高校自然科学研究重点项目（KJ2017A704，KJ2019A1303）;安徽省高校优秀青年人才支持计划项目（gxyq2018116）;安徽省优秀教学团队基金（2016jytd080）;毫州学院自然科学研究重点项目（BY22018803）

第一作者：徐建中，男，副教授，研究方向为应用数学、生态数学.E-mail： xujianzhongok@163.com.

通信作者：莫嘉琪，男，教授，研究方向为应用数学、生态数学、数学物理、工程数学.E-mail： mojiaqi@mail.ahnu.edu.cn.