幼儿数学能力的发展趋势及其影响因素：追踪研究的证据

周静娴，杨宁

【摘要】本研究采用《家庭社会经济地位问卷》《头-脚-膝-肩任务》《学童数学成就测验》对100名中班幼儿进行了一年半共3次的追踪调查，应用多层线性模型分析幼儿数学能力的变化趋势以及执行功能、家庭社会经济地位对幼儿数学能力的影响。结果显示：幼儿数学能力自中班下学期至大班下学期出现了显著的增长趋势，且存在个体差异；幼儿中班的初始执行功能水平能显著预测大班阶段的数学能力；幼儿中班初始执行功能水平对数学能力的增长速率存在显著影响；家庭社会经济地位对幼儿数学能力的预测效应不显著。

【关键词】幼儿数学能力；执行功能；家庭社会经济地位

【中图分类号】G612 【文献标识码】A 【文章编号】1005-6017（2019）07/08-0060-06

【作者简介】周静娴（1992-），女，广西柳州人，华南师范大学教育科学学院硕士研究生；杨宁（1963-），男，长沙人，华南师范大学教育科学学院教授，博士。

一、问题的提出

数学是幼儿学习与发展的重要领域之一，学前阶段的数学发展水平能有效预测儿童后期正式入学的数学成绩[1]，以及阅读[2]、科学[3]等其他学习领域的表现。关于幼儿数学能力的发展，以往研究都证实了幼儿数学能力随年龄而变化，与幼儿的成熟和经验密切相关[4][5]，但关于幼儿数学能力发展的纵向趋势研究仍甚为少见。在幼儿数学能力发展的影响因素研究中，认知因素占据主要地位，执行功能（Executive Function ，简称EF）被认为是重要影响因素之一。执行功能的主要结构包括工作记忆、抑制和认知灵活性，在多数生活情境中，三个成分共同协作以产生完整的执行功能。2～3岁是儿童执行功能发展的起始时期，同时也是数学能力发展的关键时期，执行功能水平低下，尤其是抑制控制和注意转换能力弱是影响儿童早期数学低分和数学学习困难的重要原因[6]。在环境方面，家庭在幼儿数学能力发展中扮演着重要角色，不少学者开始关注家庭社会经济地位对幼儿发展的影响。研究普遍认为家庭社会经济地位（以下简称：家庭SES）由父母的受教育程度、收入和职业构成[7]，家庭SES越高，意味着该家庭能够拥有更多的经济资源和文化资源。根据美国国家数学委员会（The National Mathematics Advisory Panel）的报告，相比高收入家庭的儿童，来自于低收入家庭的儿童在数学上的整体表现较差，更容易出现数学学习困难[8]，而这样的差异在学前教育阶段就已经存在[9]。目前，我国在社会转型中显现出社会分层和流动的趋势，来自不同阶层家庭的幼儿能否获得教育过程和教育结果的公平被认为是促进社会公平的关键，因此，家庭SES作为幼儿家庭背景的重要变量，它是否会影响幼儿的数学能力发展成为本研究探讨的问题之一。

综上可见，以往的研究已证实执行功能与家庭SES对幼儿数学能力发展具有重要意义。然而，目前我国针对幼儿数学能力的研究多停留在现状调查以及影响因素上，缺乏长期纵向研究。本研究以幼儿数学能力发展及其执行功能、家庭SES的影响为研究主题，对幼儿进行了一年半的追踪研究，应用多层线性模型（HLM）分析方法探讨幼儿数学能力随时间的发展趋势及个体、家庭因素的影响机制。

二、研究方法

（一）研究对象

根据幼儿园等级、办园性质等维度，通过分层随机抽样的方法，从广东省广州市选取10家幼儿园，其中省一级幼儿园3所、省二级幼儿园4所、省三级幼儿园3所；公办幼儿园5所，民办幼儿园5所。每家幼儿园随机抽取1个中班的10名幼儿进行执行功能和数学能力的测查，共获得100名幼儿样本（男生48名、女生52名）。同时，对100名幼儿的父母进行家庭社会经济地位调查。

（二）研究工具及施测过程

1. 研究工具

《家庭社会经济地位问卷》采用师保国、申继亮（2007）编制的家庭SES问卷[10]，家庭SES一般由父母亲职业、受教育程度和家庭收入构成，但家庭收入的测量较为困难，通常不建议使用[11]。因而问卷根据职业分类的标准和学历层次，对儿童父母职业、受教育程度进行编码，两部分所得值的总和作为家庭SES的指标值。

《头-脚-膝-肩任务》（Head-Toes-KneeShoulder）[12]由Cameron等人编制，主要考察了儿童执行功能的抑制能力、工作记忆和认知灵活性三个成分。任务要求幼儿与主试口令反着做，当听到主试说“摸摸你的头”，幼儿要去摸摸他的脚；当主试说“摸摸你的脚”，幼儿要去摸摸他的头；当主试说“摸摸你的膝盖”时，幼儿要求摸摸他的肩膀，反之亦然。在第一部分10道题中，仅使用两个提示词（头和脚）；第二部分的10道题中，也仅使用两个提示词（肩膀和膝盖）；第三部分的10道题中，以上提及的四个提示词都会使用上，每道题做错记0分；自我更正记1分；正确记2分。最高分为40分。该任务评分者间一致性系数为0.98，信度较高。

《学童数学成就测验》（Test of Children Mathematics Achievement）[13] 由谢如山（2014）编制，用于3～9岁幼儿的数学诊斷。量表共120道题目，分为非正式数学思考与正式数学思考两大领域。该量表内部一致性Cronbach’α系数为0.97，评分者间信度为0.96，可见信度较好；该量表采用幼儿数学分数作为效标，效标关联系数为0.94，效度较好。

2. 施测过程

对幼儿运用《头-脚-膝-肩任务》和《学童数学成就测验》进行一对一施测，第一次测量（T1）时间为2015年5月（中班下学期）；第二次测量（T2）时间为2015年11月（大班上学期）；第三次测量（T3）时间为2016年5月（大班下学期），并在2015年5月，向幼儿家长发放《家庭社会经济地位问卷》，发放问卷100份，回收问卷100份，回收率100%。

（三）数据处理

本研究采用SPSS19.0和HLM6.0对数据进行分析。在对个体进行追踪、多次观测的发展研究中，同一个体的不同次测量由于受同一个体共同特征的影响，有较大相似性，因而往往将这些数据看成是具有嵌套结构的，即测量嵌套于个体，通过HLM构建两个数据层可以探究个体发展趋势及个体间发展趋势差异的问题[14]。本文分析中将要涉及的变量：

第一层变量

（1）数学能力：在一年半内被测查3次，是模型第一层方程中的因变量。

（2）时间：每次测试的时间点，从第一次到第三次被编码为-2、-1、0，是模型第一层方程中的自变量。

第二层变量

（1）执行功能：第一次测试中幼儿执行功能得分，是模型第二层方程中的自变量。

（2）家庭SES：第一次调查中幼儿家庭SES得分，是模型第二层方程中的自变量。

三、研究结果

（一）幼儿数学能力发展趋势

由表1和表2看出，随着时间的变化，幼儿数学测验分数有逐渐增长的趋势，经方差分析，三次测量结果均存在极其显著差异。并且，随着时间的变化，幼儿个体间数学能力的差异渐渐缩小（标准差变小）。

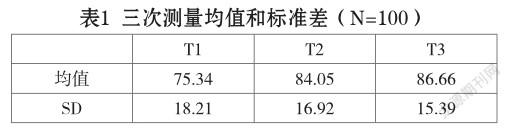
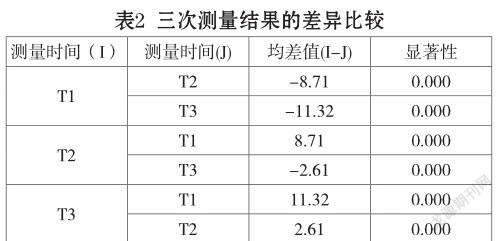
（二）数据的模型分析

1. 零模型分析

为检验研究假设，首先利用HLM的零模型（null model），它是分析的起点，能够提供对组内相关系数的估计，以确认幼儿数学能力发展是否会因个体差异而有所不同。零模型设定如下所述。

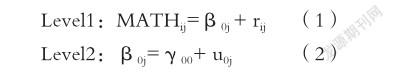
零模型的随机效应被明确区分为level1和level2两部分，分别代表幼儿数学能力的差异中源于时间变化的部分和源于个体之间差异的部分，即组内差异和组间差异。其中MATHij代表的是幼儿j（j=1，2…，100）的第i（i=1，2，3）次数学能力测量值；β0j是截距，即个体j的第一次测量值；rij是残差，即个体j在第i次测量值与线性发展曲线的离差；γ00是平均截距，即第i次测量被编码为0时所有个体的第i次测量的平均值；u0j 是个体j与平均截距的离差。模型分析结果表明个体间存在显著的变异（SD=78.790，χ2=218.908，df=100，p<0.001），并且，组内方差为81.254，组间方差为89.339，则组内相关系数ICC（intra-class correlation）计算可得：

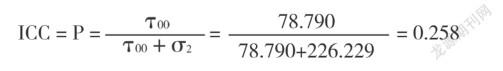
表明个体间的变异解释了总体变异的25.8%。以往研究证明，当ICC>0.059时，表明有必要在研究中使用多层线性模型以处理个体水平变异[15]。

2. 无条件增长模型分析

无条件增长模型仅在第一层放入自变量，第二层为零模型，将第一层的回归系数包含截距与斜率在第二层的回归模型都设定为随机效果，第一层模型可以描述个体随时间的线性变化趋势，而第二层模型即可解释个体之间增长参数和斜率的差异，此模型旨在检验个体是否有线性变化的趋势，以及这种线性变化是否存在个体之间差异的问题[16]。

随机系数回归模型设定如下，其中β1j表示线性增长率，即个体j在某个观测值发展变化的斜率，γ10表示所有个体的平均发展速率。分析结果摘要如表3所示。

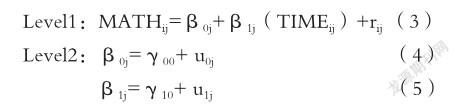
由表3可以看出，幼儿数学得分从中班上学期至大班下学期显著增长（γ10=5.908，SE=1.052，t=5.615，p<0.001）。并且，截距和斜率在幼儿个体间的变异极其显著（p<0.001），方差分别为89.111和25.887，这说明，大班下学期的最后一次数学测试分数在幼儿间差异显著，幼儿数学能力的发展趋势存在着显著的个体差异，即幼儿数学能力增长的快慢有所不同。为了探讨这种个体间差异的影响因素，需进一步分析个体变量特征对其幼儿数学能力变化的影响。

3. 全模型分析

全模型中不仅包含了第一层的时间变量，还加入了第二层的个体预测变量，这样能够通过理论建构来解释幼儿数学能力的总体变异是怎么受到第一层和第二层因素影响的。根据研究假设，该部分主要考察个体的执行功能（EF）和家庭SES对幼儿数学能力的影响，以说明幼儿数学能力增长过程中，是如何受到个体差异的影响。

全模型设定如下，其中是γ01第二层方程的回归系数，代表第二层的家庭SES和EF对第一层的截距β0j的效应；γ10是第二层方程的回归系数，代表第二层的家庭SES和EF对第一层的发展斜率β1j的效应。分析结果摘要如表4（见下页）所示。

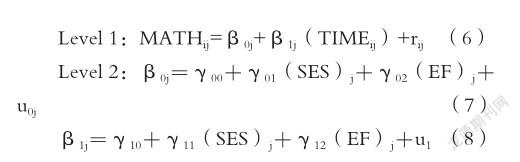
結果表明，家庭SES对幼儿数学能力的预测效应不显著（p>0.05），意味着尽管幼儿间的家庭社会经济地位不同，但一年半后，他们的数学能力并不会有显著差异，并且，幼儿数学能力发展的速率并不受家庭SES的影响。然而，初始执行功能对幼儿数学能力发展的截距预测效果极显著（p<0.001），即初始执行功能较好的幼儿，到大班下学期，其数学能力也会较强；此外，执行功能对幼儿数学能力发展的斜率预测也极为显著（p<0.01），说明初始执行功能发展水平不同的幼儿，数学能力的增长速率也存在显著差异。

四、讨论

（一）幼儿数学能力的发展趋势

本研究分析表明，幼儿数学能力自中班下学期至大班下学期一年半的时间内出现了显著的增长趋势。这不仅支持了我国幼儿数学能力存在显著年龄差异的横向调查结果（儿童认知发展研究协作组，1982；赵振国，2009），同时也与周欣（2009）的一项纵向研究发现一致，即大班阶段幼儿除部分数学能力仍在发展中，其他能力均显著优于中班阶段[17]。值得关注的是，中班下学期至大班上学期幼儿数学能力增长较快，而大班上学期至大班下学期进步较慢。

（二）执行功能对幼儿数学能力发展的影响

研究结果显示，幼儿中班初始执行功能对幼儿数学能力增长的截距有显著影响，即原执行功能水平较高的幼儿，其大班下学期表现的数学能力也较高。这与国内外众多研究结果相一致（Bull，1999；Bull，2001；Espy，2004；Gathercole，2000；Gathercole，2004；McLean，1999；Passolunghi，2001），那些能够更有效地在工作记忆中储存信息、对刺激进行选择性注意以及抑制无关信息的儿童取得的数学成就会更高。Bull（2001）指出4 岁儿童的工作记忆、抑制控制、计划和监控技能对5～7 岁时的数学能力存在影响[18]。Blair（2007）发现儿童3岁时的抑制控制与 5 岁时的数学得分存在显著相关[19]。执行功能是自我调控学习以及元认知能力的重要部分，其对幼儿大班后期的数学能力影响支持了Cunha（2007）的“能力促进能力”（skill-baget-skill）的假设，在受教育前期能力越强的幼儿，在后期习得的能力也越强[20]。

但研究结果还表明，执行功能初始水平的高低将影响幼儿数学增长的速率，即不同幼儿的数学能力水平的发展速率不同。这与国外研究一致，Blankson（2016）在一项ECLK-S两年的幼儿数学能力追踪研究中发现，幼儿2岁阶段的执行功能水平在幼儿园至学前阶段的数学能力增长中起到调节作用[21]。对于那些初始数学能力较弱的幼儿而言，较高的执行功能水平帮助他们在学习活动中保持最大化的投入，更易于在后期学前班阶段取得更高的数学成就。我国自上世纪80年代末开始推行学前教育课程改革，在一日生活中加大了区域游戏的活动时间，强调自主探索的重要意义，部分教师却受传统集体主义观念束缚，过分偏重集体教学活动，儿童主体地位有待提升。但值得注意的是，在数学领域，幼儿个体内部执行功能水平也许是儿童顺利进入小学，促进早期数学能力发展的重要保障因素[22]。

（三）社会经济地位对幼儿数学能力发展的影响

从研究结果来看，尽管幼儿来自不同社会经济地位的家庭，但他们在大班下学期数学能力测试中的成绩不存在显著差异，并且，数学能力增长的速率也不会受到家庭SES的影响。尽管社会经济地位在国外研究中普遍被认为对幼儿的数学能力发展具有较大影响，年幼孩子容易受贫困桎梏，造成阶层的封闭循环。但在我国，这种影响并未达到统计学的显著水平。这與国外众多研究结果不一致（Baroody，1987；Klibanoff，2006；Starkey，1992；Tarullo，2008）。

目前我国关于幼儿社会经济地位与数学能力的关系研究较少，研究结果支持周欣（2009）的发现，幼儿父母亲的受教育程度并不能影响幼儿的数学认知发展。其原因可以下几方面进行解释：首先，部分研究表明尽管家庭SES是家庭背景中一个重要变量，但它对幼儿发展的影响可能会受到中介变量或调节变量的作用，而非直接影响幼儿发展。幼儿家庭背景还包括了家庭条件、藏书量等客观条件，以及家长教育期待、家长教育态度与教育理念等主观条件[23]，其中，父母对子女的教育期望影响着子女自身的教育期望和教育成就。在中国，随着社会向市场化和现代化转型，城乡二元化、地区经济发展不平衡等问题逐渐显现，优势家庭子女相比弱势家庭也许能更便捷地获得优质教育资源，但是，当不同背景儿童获得同等学前教育机会时，社会经济地位较低的家庭更有可能将教育看作是子女和家庭实现向社会上层流动的主要途径，因而对子女期待更高，更重视幼儿的学业发展。其次，家庭环境除上述的家庭背景外，还包括家长与子女之间的互动关系，对于数学而言，家长尊重儿童学习兴趣，与儿童一起阅读、一起玩数学游戏等这些亲子活动方式相比父母学历而言更为重要（周欣，2009），调查的家庭中存在部分全职母亲，尽管其按照职业等级评分较低，但却更可能保证适宜的陪伴时间，保持高质量的亲子互动关系，从而提高幼儿的数学能力。

五、教育建议

（一）正确看待社会经济劣势地位的儿童发展问题

当下，我国积极推行和谐社会，教育公平已成为教育学和社会学领域的研究热点。过去普遍认为社会经济劣势地位的儿童在认知方面发展滞后，更值得注意的是，在如广州等经济发达地区还存在不少“流动儿童”，大众往往会给他们贴上“问题儿童”“成绩差”等标签。但研究结果表明，父母学历低、职业等级低并不会显著影响儿童数学能力的发展，也就是说，低社会经济地位的儿童尽管家庭物质、文化资源有限，但他们并不如舆论所述的那么糟糕，若监护人能够尽心提供温暖的家庭氛围，那么孩子顺利健康成长并不意外。因而，有必要以理性、客观的态度给予处境不利儿童关注，避免“问题化”甚至“污名化”。

（二）重视童年早期执行功能的培养

初始阶段执行功能水平较高的儿童将在后期数学能力发展上具有一定优势，2～3岁是幼儿执行功能发展的开端，其培养和训练通常需要一段时间才能够见效，因此，家长可在亲子互动中渗透执行功能的训练。例如，传统的“萝卜蹲”游戏和研究中所采用的“头-脚-膝-肩”游戏，能够较好地吸引儿童兴趣，同时，还应适当强调幼儿的生活常规，指导幼儿将用过的物品或玩具归回原处，这些能够有效地促进幼儿抑制控制和认知灵活性的发展。此外，家长也可通过设置游戏情境，与年龄较小的幼儿玩“录音机说什么”的复述游戏，与稍大一些的儿童开展棋牌、拼图等规则游戏，指导儿童有意识地进行记忆训练。

（三）提供高质量的师幼互动

初始执行功能较高儿童在众多研究中被认为会利用这些优势而获得更快速的数学能力增长，表现出“马太效应”。幼儿教师既要鼓励执行功能有优势的幼儿发挥特长，也需耐心指导有潜能的孩子探索、游戏，通过高质量的师幼互动，保障执行功能在幼儿数学能力发展中能发挥关键的促进作用。因而，幼儿教师应时常审视自身在教育实践中的行为表现，是否洞悉孩子们的个性特点，是否听到了孩子们渴望的呼唤，是否看到了孩子们好奇的目光，尽量避免“支架”提供不及时、反馈质量不高、缺乏鼓励和肯定等现象发生，做到有教无类，因材施教。

【参考文献】

[1] Duncan， Greg J， Dowsett， Chantelle J， Claessens， Amy. School readiness and later achievement. [J]. Dev Psychol， 2007 （06）：1428-1446.

[2] Duncan J， Owen AM. Common regions of the human frontal lobe recruited by diverse cognitive demands. [J]. Trends in Neurosciences， 2000（10）：475-483.

[3] Sadler P M， Tai R H. Transitions. The two high-school pillars supporting college science.[J]. Science， 2007（27）：457-458.

[4] 兒童认知发展研究协作组.4-11岁儿童数学概念稳定性的发展的研究[J].心理学报， 1982（03）： 272-284.

[5] 赵振国.3～6岁儿童数感发展的研究[J].心理发展与教育， 2008（04）：8-12.

[6] 周欣，赵振国，李娟，等.认知因素对儿童早期数学学习困难的影响[J].学前教育研究， 2013 （11）：3-13.

[7] Buchmann C， Methodological Advances in Cross-National Surveys of Educational Achievement[M]. Washington， D C： National Academy Press，2002.

[8] US Department of Education. Foundations for Success： The Final Report of the National Mathematics Advisory Panel.[J]. Us Department of Education， 2008（09）：120.

[9] Klibanoff R S， Levine S C， Huttenlocher J. Preschool Children’s Mathematical Knowledge[J]. Developmental Psychology， 2006 （01）：59-69.

[10] 师保国，申继亮.家庭社会经济地位、智力和内部动机与创造性的关系[J].心理发展与教育， 2007（01）：30-34.

[11] 孙中欣.学业失败问题的家庭社会经济地位研究[J].清华大学教育研究， 1999（01）：47-51.

[12] Burrage M S， Ponitz C C， Mccready E A， et al. Age-and schooling-related effects on executive functions in young children： a natural experiment[J]. Child Neuropsychology， 2008 （06）：510-524.

[13] 谢如山.学童数学成就测验指导手册[M].新北：心理出版社，2014.

[14] [16] 刘红云.追踪数据分析方法及其应用[M]. 北京：教育科学出版社， 2005.

[15] A. S. Bryk， S.W. Raudenbush. Hierarchical Linear Models： Applications and Data Analysis Methods （Second Edition）[J]. Economics of Education Review， 1992 （03）：767-768.

[17] 周欣， 黄瑾， 赵振国，等. 大班儿童数学认知的发展[J].幼儿教育（教育科学）， 2009（11）：35-39.

[18] Bull R， Scerif G. Executive functioning as a predictor of children’s mathematics ability： inhibition， switching， and working memory[J]. Developmental Neuropsychology， 2001 （03）：273-293.

[19] Blair C， Razza R P. Relating effortful control， executive function， and false belief understanding to emerging math and literacy ability in kindergarten.[J]. Child Development， 2010（02）：647-663.

[20] Flavio Cunha， James Heckman. The Technology of Skill Formation[J]. The American Economic Review， 2007（02）：31-47.

[21] Blankson A N， Blair C. Cognition and classroom quality as predictors of math achievement in the kindergarten year[J]. Learning & Instruction， 2016 （04）：32-40.

[22] Caron A C，Verena E，Linanne J. Preschool executive function predicts early mathematics achievement[J]. Development Psychology， 2010（05）：1176-1191.

[23] 周皓. 家庭社会经济地位、教育期望、亲子交流与儿童发展[J].青年研究， 2013（03）：11-26.

本文系广东省省级特色创新项目（教育科研类）“广东省幼儿园教育质量评价：基于CLASS的研究”（项目编号：2014GXJK031）阶段性研究成果之一。

通讯作者：杨宁，yang2007n@sohu.com

（责任编辑 张付庆）